Vehicle Variable Estimation in Diagnostic Context

Elie Accari

, Denis Hamad

and Chaiban Nasr

ULCO, LASL, B.P. 699, 50 rue F. Buisson, 62228 Calais CEDEX - France

Lebanese University, Engineering Faculty I, Tripoli - Lebanon

Abstract. Safety in vehicles has many aspects and is implemented in different

ways by manufacturers. With more safety systems to come, the vehicle will

certainly start to have an operating system to manage the whole. Neural

networks have an adaptative behavior that can be trained to meet new

conditions and have a certain inherent degree of robustness when used as

variable estimators. In this paper, we present a simplified model of the vehicle

suitable to create neural network architectures that estimate the forces applied to

the wheel as well as the vehicle body slip angle and yaw rate. For this purpose,

we use the veDyna simulator which substitutes safely and economically real test

vehicles. Typical extraneous and erroneous data are then presented to test the

robustness of the network in order to judge the applicability of this approach

from ideal, exact calculation conditions to real life situations.

1 Introduction

Safety is a topic that is being implemented more and more at many levels in vehicles

thanks to advances in computational technologies. The key difference between these

solutions is where they put the decision making, and along with it, the responsibility.

An attempt in this regard is started with the IEEE P1616 “Motor Vehicle Event Data

Recorders” draft standard. The first approach using systems such as Anti-lock

Breaking System (ABS), Vehicle Stability Assist (VSA), Traction Control System

(TCS) and Electronic Stability Program (ESP) [1], implement the control in the

vehicle, leaving the driver passive in their function, except for his actions that put the

vehicle in a condition or situation that activated these systems. The second approach

[2] targets the behavior of the driver with respect to speed, tailgating and wearing the

seatbelts. The infringement of a normal condition is reported by an audio-visual alarm

of an increasing intensity as the vehicle speed exceeds the limit in the local area, the

distance to the vehicle ahead is reduced and the seat belts is still off while the speed

increases. The application of Neural Networks in a vehicle context is not new.

Previous work has shown that the non linearity of a semi-active suspension can be

overcome by the use of neural networks as control elements [3]. Also, the neural

networks are more closely applied to parameter estimation through their use in

measuring acceleration [4], and they are also used in a fault diagnostic context [5].

In this work, we propose to estimate the state of the vehicle based on a typical

physical model, then we use MLP neural networks structures with one hidden layer to

elaborate estimators of directly measurable or calculated variables. The justification

Accari E., Hamad D. and Nasr C. (2006).

Vehicle Variable Estimation in Diagnostic Context.

In Proceedings of the 2nd International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 35-44

DOI: 10.5220/0001199800350044

 SciTePress

of this approach is that with the proper training, this system can curve fit any real

function [6], [7]. We then study the response of the estimation networks to data

unseen before in the training. Robustness is probed by changing the driver and adding

errors to the inputs.

2 Physical Model of the Vehicle

2.1 Vertical Reaction Force

Each wheel is subject to a vertical reaction force which is the resultant of the sum of

all the small forces applied over the surfaces of contact between the tread and the

road. This force is not necessarily applied at the centre of this surface and various

wheel models try to locate and model it [8]. However, its magnitude can be

determined by decoupling the front and rear axels and applying the laws of static and

equilibrium of forces as shown on Fig. 1.

Fig. 1. Static Model of the Vehicle.

This way we can estimate the force on the rear left wheel F

ZRL

to be:

YCoG

CoG

ZRL

⎟

⎠

⎞

⎜

⎝

⎛

+−

⎟

⎠

⎞

⎜

⎝

⎛

(1)

where m is the mass of the vehicle; l

, and l are the front and total lengths of the

vehicle measured from the centre of gravity whose height is given by h

CoG

; a

, a

and

g are the longitudinal, lateral and gravity accelerations; b

is the length of the rear

axle; RL refers to the Rear-Left wheel. In this equation, only a

and a

are variables

while the remaining elements are parameters. The height of the centre of gravity is

constant for a given load only when the vehicle is standing still or moving at a

constant velocity. However, it varies with the acceleration and thereby the

accelerations remain the only variables needed for the estimation of this force.

2.2 Lateral Force

Due to the fact that the wheels on one side of the vehicle are not parallel to the other,

and there is a small axis toe-in (b

≠ b

), a remnant lateral force F

is always present

and it is equal and opposite for wheels on the same axel in straight course. This

embedded value will be trained into a neural network. The estimation will be limited

to the cases when the vehicle is actually making a turn, represented by a steering

angle larger than a given minimum. The horizontal and lateral forces are linked to the

vertical reaction by the friction coefficient of adhesion:

and

(2)

where F

, F

and F

are the longitudinal, lateral and vertical forces applied to the

wheel. Note that this ratio is constant only for the low values of the forces.

2.3 Wheel Slip

The relationship between wheel slip and the friction coefficient is the subject of

various studies [9], [10]. Though the definition is the same in all references as being

the difference between a wheel's rotational and translation speeds, as given by:

vdt

dtrvdt

−=

−

= 1

(3)

where s is the slip, v is the vehicle’s speed, r is the wheel radius,

is the wheel’s

angular velocity and dt is an interval of time.

The forced rotation of the wheel generates the longitudinal force shown in Fig. 2.

Fig. 2. Wheel’s static radius and applied forces.

stat

is the static wheel radius, defined as the distance between the centre of the wheel

and the road for a given load at stand still. We note however that because each wheel

is subject to a different vertical reaction force, they are compressed differently on the

front and rear axles and therefore their radii are not the same. Any variation in this

parameter implies a variation in the wheel’s speed and we only consider the rotational

speed as variable and the remaining elements as either parameters or implicit.

We conclude that the vehicle’s speed, the wheel's rotational speed and the vertical

force have the major influence in determining wheel slip.

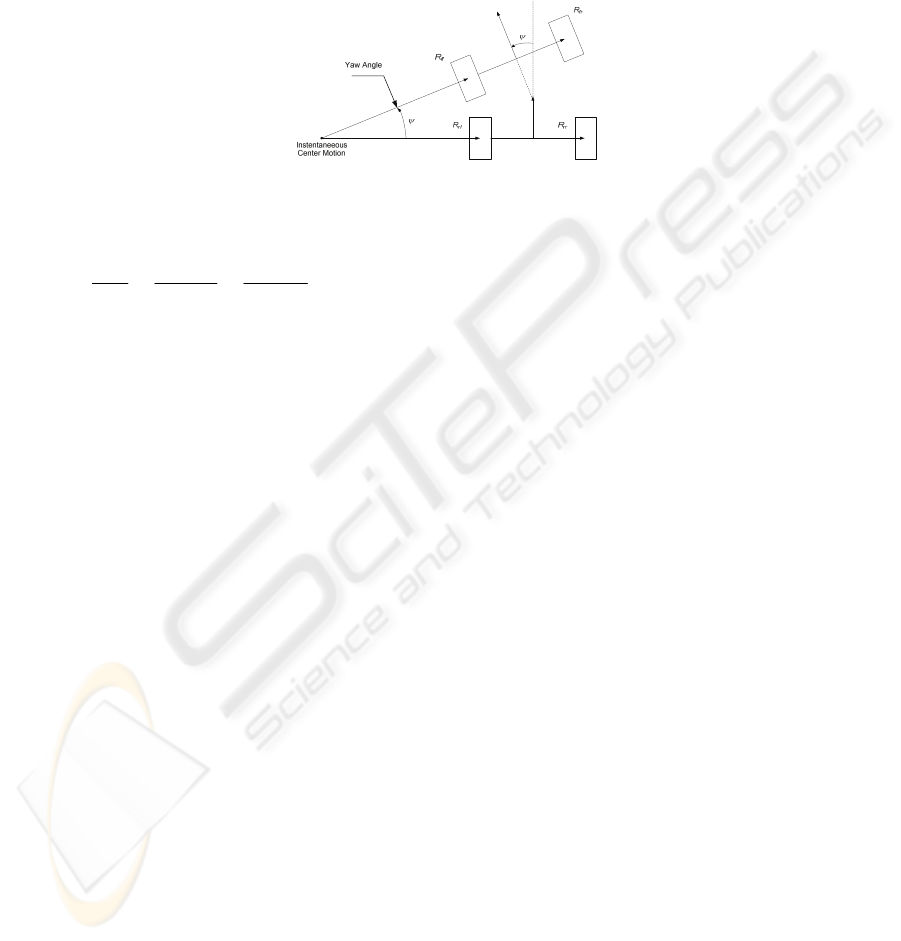
2.4 Yaw Rate

We attribute to every wheel R

a rotational speed

. As the vehicle makes a turn

about a central point, the angular movement around the vertical axis becomes

proportional to the wheels’ speeds, in either their rotational or linear form. Thus the

yaw angle

is linked to the wheel rotation speed

and to the apparent turn radius of

curvature conform indicated on Fig. 3.

Fig. 3. Yaw movement in curve motion.

By observing this motion over time, we can establish the following relations:

rrstat

rlstat

(4)

where

is the angular yaw, r

stat

is the wheel’s static radius,

is the rotational speed

of the rear right wheel,

is the rotational speed of the rear left wheel, R

is the

radius of curvature of the path followed by the rear right wheel.

If need be, the yaw movement of the driveline can be upgraded to the vehicle’s

body where another component, an angle usually designated β measuring the side slip

of this body as it tends to resist, or follow with a backlash, the velocity vector of the

driveline. β is considered to be included in the yaw motion and without going through

its relationship with the suspension system it can be estimated from the physical

factors that cause it in the first place.

3 Simulated Driving Maneuvers

The German company TESIS Dynaware presents the vehicle simulation software

veDyna [11]. This simulator takes the most recent mathematical models to calculate

the behavior of the car step by step until the maneuver is over, thus providing accurate

information on what may happen on the road under the given circumstances. The

model we used is that of a BMW 325i model 1988, and we did not modify it in order

to remain as close as possible to a real life situation. The veDyna simulation software

uses about 1500 variables in order to render its virtual simulations close to real life

conditions. With its Matlab interface and open connectivity though the declared

functions, it offers unmatched flexibility allowing it to reproduce at a cheap cost a

large variety of normal and abnormal driving situations. This way, it spares fastidious

and dangerous maneuvers on real test vehicles. Typical maneuvers of slalom and

acceleration-deceleration speed profiles were used to generate an extensive training

data set for neural network estimators. The performance of these networks is tested on

a double lane change maneuver. In the following, we give a brief description of the

training maneuvers, with emphasis on the cease acceleration maneuver used in testing

the robustness against changing the driver.

3.1 Generation of the Training Database

In order to create the training and testing databases, we used the veDyna and Matlab

software to generate several road profiles and maneuvers:

• A slalom profile is generated such that the course is sinusoidal while the driver

maintains a constant velocity.

• A straight velocity profile is designed to solicit the vehicle in longitudinal

accelerations and decelerations.

The data generated by the vehicle performing these maneuvers are gathered to form

the training. In all, 56 variables were sampled at a period of 1ms, some of which have

taken part in the training processes while others were used to draw and recreate the

path followed by the vehicle on track. Thus we generated 5500 input vectors of 56

components each for the velocity profile maneuver and 4000 input vectors for the

slalom maneuver. However, we did not use these sets in complete because we can

eliminate the parts that correspond to a monotone or redundant situation on the road

in order to accelerate the training process and reduce the amount of resources required

by this task.

3.2 Generation of the Validation Database

The databases used to test the performance of the neural networks are generated using

the Double Lane Change and Cease of Acceleration maneuvers described below.

Theses maneuvers were chosen because they do not figure explicitly in the training

database.

3.2.1 Description of the Double Lane Change Maneuver

The double lane change profile is an overtaking maneuver in which the driver changes lanes

twice in order to overpass a virtual vehicle ahead. It is made of 2300 data samples.

3.2.2 Description of the Cease Maneuver

The Cease maneuver is mainly about releasing the acceleration pedal abruptly while

in the middle of a curve. The driver starts at t = 0 on a straight course, and accelerates

until the vehicle reaches the speed v_dep at time t_dep. This speed is maintained over

a time t_hold until the driver goes on a constant acceleration phase for a period of

t_acc. At this point, the vehicle is in the middle of a curve and the driver suddenly

releases the acceleration pedal letting the vehicle roll for a time t_free before bringing

it to a stop in an interval of time t_fin. The numerical value for the variables involved

is given here for reference:

t_dep=10s t_hold=5s t_acc=5

t_free=5s t_fin=6s v_dep=72Km/h

The total maneuver time is 1s more than the sum of the parts because, as per the

simulator’s documentation the system must first start and remain idle until all

calculation transients have elapsed [11]. A total of 3200 samples were generated for

this maneuver. The driver model used to perform this maneuver is based on the

fundamental primitives directly available from the simulator, mainly: (i) CRUISE and

ACCPEDAL for longitudinal control and (ii) STRAIGHT, LINTABLE and FIXED

for lateral control. In-depth information about these functions can be found in the

referenced documentation. The main difference between these directives and the

“advanced driver” model available in veDyna is that while the former behaves simply

as it is told, the latter uses PID control to maintain the centre of gravity of the vehicle

aligned with the centre line of the road path, while observing given temporal or

special constraints.

4 Experimental Results

In this paragraph we use the Multi-Layer Perceptron architectures with one hidden

layer to estimate the vertical reaction force F

, lateral force F

, wheel slip and the

vehicle yaw. For our application, we apply the BFGS training algorithm described in

[12]. The results are compared to the values generated by the simulator, hence

substituting safely and more economically a real vehicle. Note that it is a good

strategy to test the ability of the network to estimate the desired function by hiding

known, simulator generated, data in the training phase and leave it for guessing at a

later stage. One more reason for doing so is that the data in our test sets are within the

extreme limits already fed to the network through the training sets; for example, the

turns in slalom are harder and the speed and breaking in the velocity profile are more

abrupt than the ones in the double lane change, for example. Finally, besides straight

driving, overtaking or double lane changes is one of the most performed maneuvers

on the road.

The cease acceleration maneuver is also very common and hence it is used in

testing the robustness of the neural networks against a change in the driver model.

4.1 Test of Vertical Reaction Force F

Each wheel has a dedicated neural network made of 2 inputs a

and a

, 19 neurons in

the hidden layer and one output.

The results comparing the output of this network to the output of the simulation

software in the case of the double lane change maneuver for the rear left wheel are

given in Fig. 4. In this case, the estimator is able to calculate Fz accurately when the

vehicle body is not strongly sollicitated, otherwise it will commit a maximum error of

10%. Note that all simulation figures, and in this case Fig. 4, are a snap shot of

continuous motion over the whole simulation time, which can sometimes go around

one minute of driving and contains too much of non critical information to show on a

figure. On the other hand, we are observing 56 variables at veDyna’s default

calculation step of 1ms, so the software anticipated that this large size of 10 bytes

IEEE Real variables is not entirely necessary to store in a log file, so we use its

default rate of 1 in every 10 samples for observing the variables. Hence, the 0 in x-

axis of the figures corresponds to the time t0 as of which the data starts to be

interesting for us and the sampling time is to be multiplied by 10 to read the real

simulation time; thus 200 corresponds to 2000ms after t0.

4.2 Test of the Lateral Force F

The inputs are the lateral acceleration a

and the steering angle lrw, with 40 neurons

in the hidden layer and one linear output. The results of the estimation of this force on

the double lane change maneuver are shown in Fig. 5, with an average error of 15.8%.

4.3 Test of Wheel Slip “s”

Each wheel has a dedicated neural network of its own, having 3 inputs and 53 neurons

in the hidden layer. The longitudinal component of the speed of the vehicle's centre of

gravity is a common input to all four networks; the remaining two inputs are the

specific wheel's rotational speed and the applied vertical force F

≡F

ZXY

, with

XY=RR, RL, FL or FR. The results of the simulation on the double lane change

profile are shown in Fig 6. We conclude that the wheel slip can indeed be calculated

with a ±6% tolerance from the vehicle's overall speed and the wheel's rotation speed

under given load conditions F

ZXY

It can be inferred from the Fig. 6 that the maximum slip is well below 10% and we

are in the linear edge of the slip curves, so a less complicated approach is feasible.

Yet it should be noted that the value of sl is only small because veDyna’s “advanced

driver” is programmed to keep the vehicle near its optimal functional point, where it

has the most traction (and hence stability) on the road and the efficiency of the engine

as seen from the wheels is maximal. A human driver will not always be able to do so

and will need to be followed throughout the entire slip margin.

4.4 Test of Yaw Rate “dψ/dt”

The inputs to the neural network are three of the four wheels' rotational speed, since

the fourth wheel is forcibly dragged by these three and the vehicle body since it is not

deformable. However, we noted that the network is better run if it is given the

difference between these variables, two by two, instead of giving them in raw format

and let the network figure it out. This idea was used because in order to obtain a

rotation, the wheels’ speed must be all different, and the bigger this difference is the

more the yaw. This way we formed the difference: ω

-ω

and ω

-ω

. The third

input is the lateral acceleration. The hidden layer contains 37 neurons and the output

is shown in Fig. 7. We observed that the estimation of the yaw rate is within a good

±5% tolerance, mainly due to the influence of geometry on this value, rather than

internal variables and given that the slalom training set is exhaustive in this respect

with regard to the large yaw rate values it contains.

4.5 Simulation Results – Figures

Following are the figures summarizing the results discusses above, where the

discussion given in §4.1 applies.

0 500 1000 1500

1500

2000

2500

3000

3500

4000

4500

Fz [N]

ve Dy n a

MLP

0 100 200 300 400 500 600

-3000

-2000

-1000

1000

2000

Fy [N ]

veDy na

MLP

Fig. 4. Estimation of the vertical reaction

force.

Fig. 5. Estimation results for F

0 500 1000 15

-0.05

0.05

0.1

0.15

Longitudinal Slip

ve Dy n a

MLP

0 200 400 600 800 1000 1200

-0.4

-0.2

0.2

0.4

Yaw Rate [rad/s]

ve Dy n a

MLP

Fig. 6. Estimation of wheel slip s.

Fig. 7. Estimation of Yaw Rate dψ/dt.

4.6 Summary

The neural networks described above share a lot of common inputs; therefore they can

be modularly integrated in a single structure as shown in Fig. 8.

Fig. 8. Integrated Neural Network for Vehicle Variable Estimation.

For example, all four networks that calculate the lateral force F

on the wheel have

the same inputs: the steering wheel angle and the lateral acceleration, the only

difference between them is the weights; due to the way each one was trained. Thus we

need to read the value of lrw and a

only once and from there we calculate 4 outputs.

The same is generalized for the other networks described in this paper.

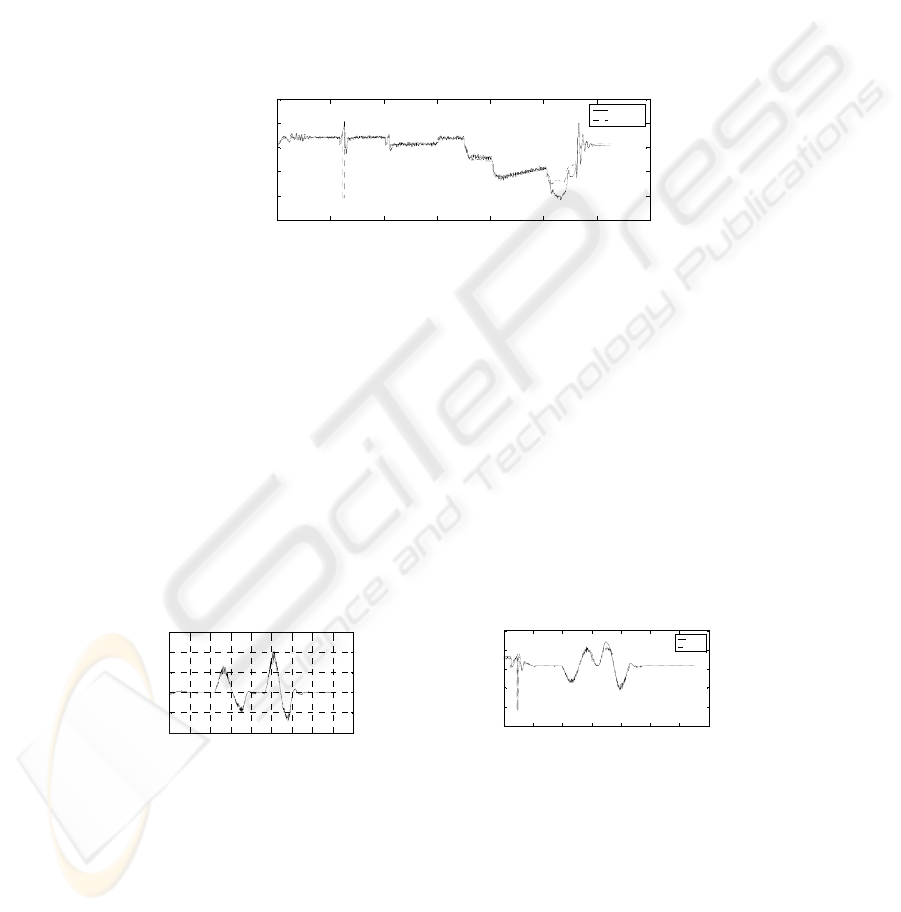
5 Robustness of MLP Networks

5.1 Test Against Change in the Driver Model

Neural Networks have been used to improve driver models [12], [13]; however we

limit our study to the PID driver model implemented in veDyna.

This test is done using the Cease maneuver presented above. The a

and a

components of the acceleration are passed to the same estimator of the vertical force

. The result is shown on Fig 9.

As we can see, the network is able to follow the target result with a total error of

3.86%, but inconsistency appears around the point where the driver suddenly releases

the acceleration pedal, because the network was not trained for this event.

0 500 1000 1500 2000 2500 3000 3500

1000

2000

3000

4000

5000

Fz [N]

ve Dy n a

MLP

Fig. 9. Estimation results of F

on the Cease maneuver.

5.2 Test Against Errors at the Inputs

The robustness the MLP networks against errors at their inputs is studied using the

MLP estimator of Fz applied to the double lane change maneuver as a typical

example. The source of error on the inputs can be due to either background noise,

inaccurate sensors or to the method of measurement itself.

We will take the acceleration components a

and a

from the double lane change

maneuver and add as much as 20% of uncertainty to the measured values of a

and

, as per the following equation:

a=(0.8+0.4*rand(2, data_size)).*a;

(5)

where a is the acceleration vector. The effect of this modification on the longitudinal

acceleration is shown on Fig 10 and the estimated force Fz comes with an overall

error of 1.9% as shown on Fig. 11.

0 100 200 300 400 500 600 700 800 900

-1

-0.5

0.5

1.5

a x w ith n o is e [m /s 2 ]

0 200 400 600 800 1000 1200 1400

1000

2000

3000

4000

5000

Fz [N ]

veD y na

MLP

Fig. 10. Effect of 20% inaccuracy on a

Fig. 11. Estimation of F

with input error.

Similar tests were repeated on other networks with results equivalent in nature,

however an exhaustive study of the tolerance limit is put for future work.

6 Conclusion

We used simulated driving maneuvers to test MLP networks for parameter estimation

in a vehicle supervision context. For this purpose, the vertical reaction force, the yaw

rate and the wheel slip have been estimated by neural network systems. The choice of

inputs for the MLPs was inspired from the physical model and the size of the hidden

layers was fixed after an exhaustive range scan up to 60 neurons. With regard to

robustness, and although only a limited number and somewhat particular cases were

studied, all results show that neural networks have an inherent degree of immunity

towards various types of errors. Thus this work concludes that a vehicle operating

system can make use of MLP estimation networks as inputs. This system can be

complementary to the multimedia and GPS services now being offered to passengers.

Its implementation should benefit from the speed of widely available neural network

integrated circuits, leaving any bottleneck to the upper software level.

Finally, the estimation results are best when the data under test is generated by the

same driver as the one used in the training phase. Therefore it is essential that the

networks be trained, under generic procedures, by the drivers that will use them.

References

1. Robert Bosch GmbH: ESP Electronic Stability Program, attributed to group effort (1999)

2. Sala, B.: Digital Device Development Group, Implementing Intelligence in Vehicles, The

Magazine of Engineers Australia, Vol. 76, N° 9, (2004) pp. 26-29

3. Guo, D. L., et al.: Neural Network Control for a Semi-Active Vehicle Suspension with a

Magnetorheological Damper, Journal of Vibration and Control, Vol. 10, No. 3, (2004) pp.

461-471

4. Gao, X. Z., et al: Acceleration signal estimation using neural networks, Measurement.

Science and Technology 12, (2001) pp. 1611-1619

5. He, Y., et al.: Engine Real-time Fault Diagnosis using Neural Networks, Automation

Technology for Off-Road Equipment, Proceedings of the July 26-27 Conference, Chicago,

Illinois, USA (2002), pp. 89-95

6. Weigl, K., Berthod, M.: Neural Networks as Dynamical Bases in Function Space, INRIA,

report N° 2124 (1993)

7. Hornik, K., et al.: Multilayer Feedforward Networks are Universal Function

Approximators, IEEE Transactions on Neural Networks, Vol 2, No. 5, (1989) pp. 359-366

8. Kiencke and Nielsen: Automotive Control Systems, SAE International, Springer (2002)

9. Canudas, C.: Dynamic Tire Friction Models for Vehicle Traction Control, Laboratoire

d’Automatique de Grenoble, Conference on Decision and Control, Phoenix, Arizona (1999)

10. Kim, Y. S., et al.: Development of RT vehicle simulation system for integration of ABS

HIL and a driving Simulator, Department of Automotive Engineering, Kookmin University,

Seoul, Korea.( 1998)

11. TESIS DYNAware veDyna Example Book - Standard Road (2002)

12. Rivals, I., et al.: Real-time control of an autonomous vehicle: A Neural Network Approach

to the Path Following Problem, 5th International Conference on Neural Networks and their

Applications, NeuroNîmes (1993)

13. Lin, Y., et al.: Artificial neural network modeling of driver handling behavior in a driver-

vehicle-environment system, International Journal of Vehicle Design - Vol. 37, No.1,

(2005) pp. 24 – 45