
N-ARY TREES CLASSIFIER
Duarte Duque, Henrique Santos, Paulo Cortez
Department of Information Systems, University of Minho, Campus de Azurém, Guimarães, Portugal
Keywords: Video surveillance, Behaviour detection and prediction.
Abstract: This paper addresses the problem of automatic detection and prediction of abnormal human behaviours in
public spaces. For this propose a novel classifier, called N-ary trees, is presented. The classifier processes
time series of attributes like the object position, velocity, perimeter and area, to infer the type of action
performed. This innovative classifier can detect three types of events: normal; unusual; or abnormal events.
In order to evaluate the performance of the N-ary trees classifier, we carry out a preliminary study with 180
synthetic tracks and one restricted area. The results revealed a great level of accuracy and that the proposed
method can be used in surveillance systems.
1 INTRODUCTION
Are the traditional systems and approaches to video
surveillance adequate to real needs? The answer is
no. In the 70’s, two researchers published a study
(Tickner and Poulton, 1973) about the efficacy of
human surveillance when dealing with a large
number of cameras. The study has demonstrated that
the level of attention and the accuracy of abnormal
event detection decreases along the time. The
authors of this work also verified that human factors,
such age and sex, can influence the reliability of
incident detection.
Considering those facts, a new generation of
proactive surveillance systems can emerge. Some
attempts to automatically detect and predict
abnormal behaviours were already performed.
The ADVISOR project (Naylor, 2003), whose
aim was to detect vandalism acts, crowding
situations and street fights, was one of the most
relevant works in this field. The system made use of
a 3D model of a monitored area, where abnormal
actions were previously defined by security experts,
who described those acts using a description
language. This sort of approach led to a context
dependent detection system, where all the objects
from the scene and relations between those objects
must be defined.
A more recent work (Mecocci et al., 2003)
introduces an architecture of an automatic real-time
video surveillance system, capable of autonomously
detect anomalous behavioural events. The proposed
system automatically adapt to different scenarios
without any human intervention, and uses self-
learning techniques to learn the typical behaviour of
the targets in each specific environment. Anomalous
behaviours are detected if the observed trajectories
deviate from the typical learned prototypes.
Despite de relevant contribution, the work
presented in (Mecocci et al., 2003), does not
accomplish the particular features of a surveillance
system, where typically the monitored area
comprises different levels of security, i.e. the
existence of restricted and public areas. Another
negative aspect of this approach is the use of simply
spatial information, which is a significant lack of
attributes for describing danger actions.
To overcome the identified problems a novel
behaviour classifier, called N-ary trees, was
developed. The proposed classifier processes time
series of attributes like object position, velocity,
perimeter and area, to infer the type of action
performed. The N-ary trees can detect three types of
actions: normal; unusual; or abnormal events.
The paper is organized as follows. In Section 2,
we present the proposed method to predict abnormal
behaviours, and describe the creation of the N-ary
trees classifier. Experimental results are presented in
Section 3 and, in Section 4 we draw some
conclusions.
457
Duque D., Santos H. and Cortez P. (2006).
N-ARY TREES CLASSIFIER.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 457-460
DOI: 10.5220/0001200904570460
Copyright
c
SciTePress
2 THE CLASSIFIER STRUCTURE
The behaviour of an object can be described by a set
of actions that it performed in a certain environment.
By the security point of view we could expect, at
least, three kinds of observations: normal; unusual;
or abnormal actions.
Normal actions are those which are frequently
observed and do not origin the violation of any
restricted area. Actions that are unusual are those
that are not common or have never occurred. When
an action leads to a violation of a restricted area,
then it should be classified as an abnormal action.
The proposed classifier needs to be able to
predict those events from the registered object path.
This leads us to a classifier that should respond to
the following question: If an object, with specific
properties, travels until a certain point, what is its
probability to follow a path that will cause an
abnormal event?
We propose a classifier that aims to answer this
question, using an N-ary tree, whose nodes are
composed by two kinds of information:
multivariable Gaussian distributions N(μ, Σ) in the
object attribute’s hyperplane; and an abnormal
probability (P
ab
), i.e. the probability of an object,
that cover a know path, and is situated in a region
defined by the Gaussian distribution of the node in a
given period of time, to violate a restricted area.
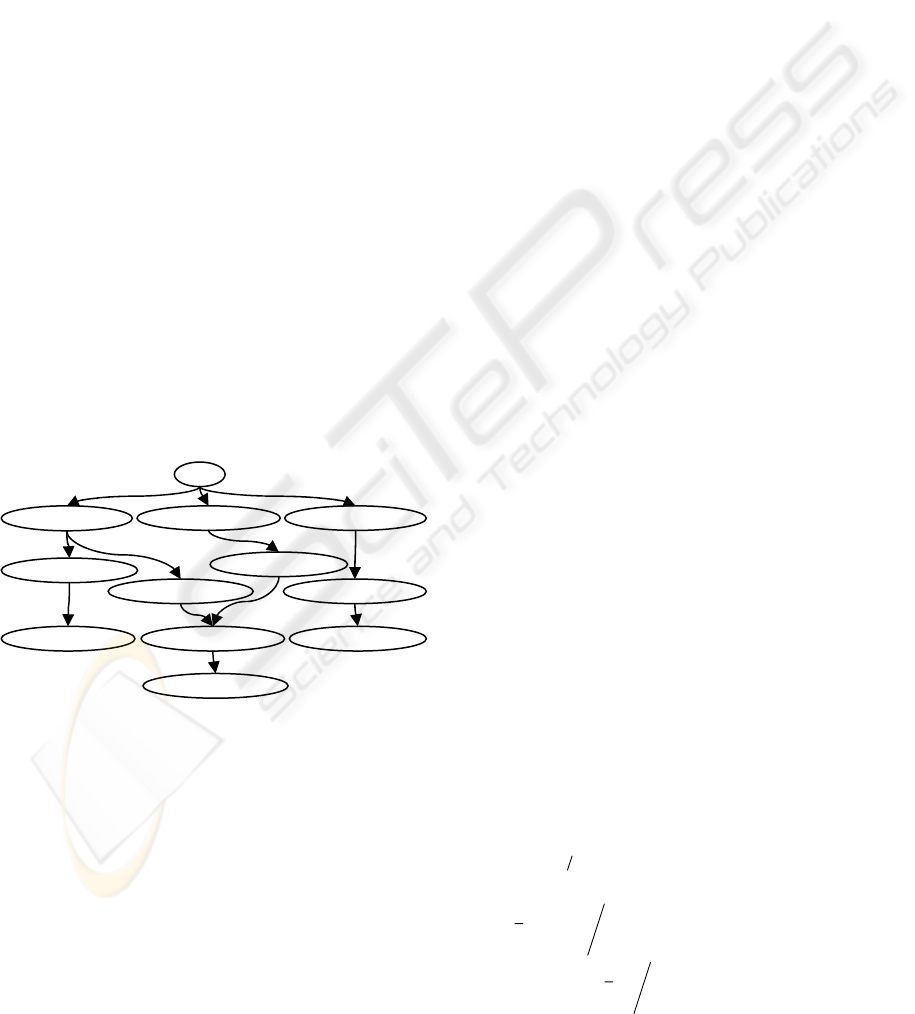
Figure 1: Example of an N-are trees classifier.
Has we can see in figure 1, the classifier’s tree is
organized by layers. Every track should be described
by a sequence of nodes, each one from a different
layer, starting in “layer 1” (when an object enters in
the scene). In this classifier, the layers define the
regions of object’s attributes for a given time period,
e.g. 10 frames.
The proposed N-ary trees, can be seen as a
spatiotemporal classifier enriched with some
object’s attributes. To build that classifier, we use a
set of pre-recorded tracks, where each track is
defined by a sequence of attribute vectors,
describing the properties of an object at each sample.
For now the following attributes are considered: 2D
coordinate’s center-of-gravity; velocity; area; type
descriptor, i.e. human, group or vehicle; and an
alarm flag. Note that the tracks used to learn the
classifier are flagged only in two states: normal or
abnormal tracks.
The first step on constructing the N-ary trees
classifier consists on the partitioning of the data into
equal time slices. Then, for each time slice, the
sampled data of every track is averaged. Next, the
computed data from all the tracks observed in the
given time slice are clustered, forming different
Gaussian distributions.
Since there is no information about the number
of clusters in a layer, a cluster algorithm capable to
infer the number of expected distributions should be
used. For this propose an Expectation-Maximization
algorithm with automatic cluster number detection
based in k-fold cross-validation (Kohavi, 1995) was
implemented, with k = 10, as described next.
2.1 Clustering the Data
Consider X a d-component column vector of object
attributes, μ the d-component mean vector, Σ the d-
by-d covariance matrix, and |Σ| and Σ
-1
its
determinant and inverse, respectively.
For each layer there are N tracks samples, and
initially the number of classes (C) is set to one. The
first step of the k-fold cross-validation is to divide
the dataset into ten fractions. Next, nine fractions are
selected to compute the expectation and
maximization steps. The remaining fraction is used
to compute the log-likelihood. This procedure is
executed ten times in order to compute the log-
likelihoods of all the fractions from the dataset.
The final log-likelihood is calculated as the mean
of the ten log-likelihoods. The value of classes C
will be incremented while the log-likelihood L is not
stabilized. After determining the number of clusters,
the computation of the Gaussian distributions is
performed by the Expectation-Maximization
algorithm, as described bellow:
Starting conditions:
()
()
()
NX
NX
Xrandom
CWP
doCjforeach
N
i
jij
N
i
ij
j
j
∑
∑
=
=
−=Σ
=
=
=
∈
1
2
1
1
μ
μ
μ
P
ab
, N1,1(µ1,1,Σ1,1)
P
ab
, N1,2(µ1,2, Σ1,2)
P
ab
, N1,m(µ1,m, Σ1,m)
Layer 1
Root
P
ab
, N2,1(µ2,1, Σ2,1)
P
ab
, N2,2(µ2,2, Σ2,2) P
ab
, N2,n(µ2,n, Σ2,n)
P
ab
, N2,3(µ2,3, Σ2,3)
P
ab
, N3,1(µ3,1, Σ3,1) P
ab
, N3,2(µ3,2, Σ3,2) P
ab
, N3,k(µ3,k, Σ3,k)
P
ab
, N4,1(µ4,1, Σ4,1)
Layer 2
Layer 3
Layer 4
ICINCO 2006 - ROBOTICS AND AUTOMATION
458

Expectation step:
()
()()
[]
()
()()
()
()
()
()()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−⋅Σ⋅−
−
=
−
⋅
Σ⋅
=
⋅
=
∈
⋅=
∑
2
2
1
2
1
1
2
1
|,
|
|
|
jj
T
j
XX
j
d
j
jj
j
K
j
jj
eWXPwhere
XP
WPWXP
XWP
doCjforeach
WPWXPXP
μμ
π
Maximization step:
()
()
()
[]
()
()()()
()
j
N
i
T
jijiij
j
j
N
i
ij
j
N
i
ij
j
WPN
XXXWP
WPN
XWPXi
N
XWP
WP
doCjforeach
ˆ
ˆˆ
|
ˆ
ˆ
|
ˆ
|
ˆ
1
1
1
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−⋅−⋅
=Σ
⋅
⋅
=
=
∈
∑
∑
∑
=
=
=
μμ
μ
Stopping criteria:
()
()
()()
()
ε
<−
=
∑
=
old
N
i
i
LLwhile
XPL
SteponMaximizati
StepnExpectatio
do
1
ln
_
_
When the stop condition is satisfied, the means
and variances of the distributions of a layer are
founded. After executing the clustering over the
entire dataset, we obtain a set of clusters for each
layer. The next step consists on building the
classification tree, defining links between clusters of
different layers.
2.2 Linking the N-ary Tree
To build the classification tree, it is necessary to go
trough all the track sequences of the dataset. For
each track, we will try to find a path (sequences of
clusters, each cluster from a different layer) that
represents it. When a dissimilar path is observed, a
new branch of the tree is created.
During this linking process, the information
about the event type of each track and at each time
slice is recorded within the clusters. At the end, all
nodes of the tree will have the information about:
mean and variance of the Gaussian distribution; and
number of normal and abnormal events observed.
This way, it is possible to infer the probability of an
object to exhibit an abnormal behaviour, when
associated with a certain path.
3 EXPERIMENTAL RESULTS
In this section we present the preliminary
experiments to evaluate the proposed N-ary trees
classifier. The dataset used to evaluate the classifier
was artificially generated. To this propose
semiautomatic track generator software, designated
by OBSERVER-TG, was developed. This tool
allows the user to generate tracks in a scene, with
configurable Gaussian noise over the center-of-
gravity position, velocity, area and perimeter of the
object.
A dataset of 180 tracks with different lengths
were created in a scene with a restricted area, as
shown in figure 2. The set of generated tracks
represent six different paths. Ten of the generated
tracks violated the restricted area, originating an
alarm event. All the abnormal tracks started at
bottom left of the scene, cross the road and turn left
into the protected area.
To evaluate the accuracy of the proposed
classifier, the dataset was randomly fractioned in
three parts. Then, a hold-out validation scheme
(Kohavi, 1995) was adopted, where 2/3 of the
simulated data was used for training (e.g. learning
phase) and the remaining 1/3 for testing.
Figure 2: Background image overlapped by 180 tracks
from the dataset. The red box indicates a restricted area.
N-ARY TREES CLASSIFIER
459

Figure 3: 2D clusters representation of the 12
th
layers from the generated N-ary trees classifier.
Tracks that have probability of abnormal
behaviour greater than zero are classified as
abnormal events. Sequences that have unobserved
paths are classified as unusual events.
The test results obtained in the three simulations
(A, B and C) are presented in the table bellow.
Table 1: Test results of the N-ary trees classifier.
Test Set Test Results
NºTracks Abnormal Unusual Abnormal
A 60 5.00% 1.66% 3.33%
B 60 8.33% 5.00% 3.33%
C 60 3.33% 1.66% 1.66%
We can see, for instance, in the simulation A
with a test set that has 5% of abnormal tracks, that
the results obtained by the proposed classifier were
reasonable. The system has successful detected
3.33% of tracks as abnormal events, and 1.66% as
unusual events. Summating the abnormal with the
unusual detection results we obtain the total of 5%.
Analysing the results we detect that all the
normal tracks from the dataset was correctly
classified. This outcome can be a consequence of the
similarity of the generated tracks.
In a real world situation, when the type of
observed paths is more chaotic, we can expect that a
considerably amount of safety tracks are classified
as unusual events. In such situation, the system user
should be prompted to classify this kind of events as
normal or abnormal behaviours, for use in future and
refined classifiers.
4 CONCLUSIONS
In this work we present a new approach to
automatically detect and predict abnormal
behaviours of humans, groups of people and
vehicles.
The proposed solution is based on an N-ary trees
classifier which has performed well with artificial
test data. Moreover, the N-ary trees classifier
possesses complementary features that can be
exploited to find the most utilized paths and to
analyse the occupancy of the monitored areas.
The classifier prototype was constructed as a
standalone application due to the expensive
computation required by the clustering process and
the necessary evaluation tasks. However, once
finished, it seems to be extremely fast, comprising
the real-time constraints of a surveillance system.
The proposed classifier has ideal features to
integrate under surveillance tasks, where there are
few or even none observed alarm events. In such
cases it is necessary the intervention of a user to
classify unusual events.
Despite the confidence level on the results
obtained, the validation of this solution still lacks of
a deeper test with real data. In future we expect to
extend the test of the proposed classifier to different
scenarios, with a greater number of paths, from
simulated and real data.
REFERENCES
Tickner A.H., Poulton E.C. (1973). Monitoring up to 16
synthetic television pictures showing a great deal of
movement. Ergnomics, 16:381-401
Naylor M. (2003, June 24). ADVISOR – Annotated
Digital Video for Intelligent Surveillance and
Optimised Retrieval. Retrieved February 7, 2006, from
http://www-sop.inria.fr/orion/ADVISOR
Mecocci A., Pannozzo M., Fumarola A. (2003).
Automatic detection of anomalous behavioural events
for advanced real-time video-surveillance. In
International Symposium on Computational
Intelligence for Measurement Systems and
Applications, Lugamo, 187-192.
Kohavi R. (1995). A study of cross-validation and
bootstrap for accuracy estimation and model selection.
In Proceedings of the Fourteenth International Joint
Conference on Artificial Intelligence, San Francisco,
1137-1143.
ICINCO 2006 - ROBOTICS AND AUTOMATION
460
