KEY PERFORMANCE INDICATORS IN PLANT-WIDE

CONTROL

Sebastjan Zorzut, Vladimir Jovan

Jozef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia

Alenka Žnidaršič

Metronik d.o.o., Stegne 9a, SI-1000 Ljubljana, Slovenia

Keywords: Key performance indicators; Production management; Decision support systems; Closed-loop control.

Abstract: To improve production performance it is necessary to define production goals with a proper implementation

strategy and a suitable closed-loop control for their achievement. A promising solution is the use of the Key

Performance Indicators (KPIs) approach. To verify the idea of production feedback control using production

KPIs as referenced controlled variables, a procedural model of a production process for a polymerisation

plant has been developed. The model has been used during a number of simulation runs performed with the

aim of developing and verifying the idea of KPI-based production control.

1 INTRODUCTION

A production process involves several business and

technical activities on and around the factory floor.

Its effectiveness can be assessed using information

hidden in a set of current and historical production

data. The problem of extracting the relevant

information from production data for fast and

accurate decision-making can be solved by

introducing a set of production KPIs (Vicens et al,

2001; Lohman, 2003) that show the operational and

mid-term efficiency of the production. On the

strategic management level, the problem of overall

business efficiency in a production factory is already

being solved with this approach (DeBusk, 2003),

while on a production management level the

implementation of KPIs is a rather new concept. The

solution lies in defining an appropriate set of KPIs

that are specific to the observed production process,

and in defining the strategy for using KPIs to

efficiently manage that process. Recently, a

balanced set of general KPIs for the production

management level has already been introduced

(Rakar et al, 2004) and five principal KPIs for

process-oriented productions were defined: Safety

and Environment; Production Efficiency; Production

Quality; Production Plan Tracking; and Employees

Issues.

2 CLOSED-LOOP PRODUCTION

MANAGEMENT PARADIGM

The desired global production objectives in the

context of production management system can be

more objectively defined as the reference values for

significant measures of plant efficiency, production

plant productivity, mean product quality and others.

These production objectives are often called implicit

objectives as they usually can be expressed only

implicitly as functions of the measurable and

manipulatable variables (Stephanopoulos and Ng,

2000). Since implicit objectives are not directly

measurable, their translation into a set of output

production process variables should be provided.

These output production process variables should

have the following properties (Skogestad, 2004): (i)

they should be more easily measurable, (ii) it must

be possible to handle maintaining their set point

values by proper adjustments of manipulatable

production process variables, and (iii) when

maintained at the desired optimal set-points through

the feedback control subsystem, they should

inherently contribute to the overall profitability of a

production process. These variables are denoted in

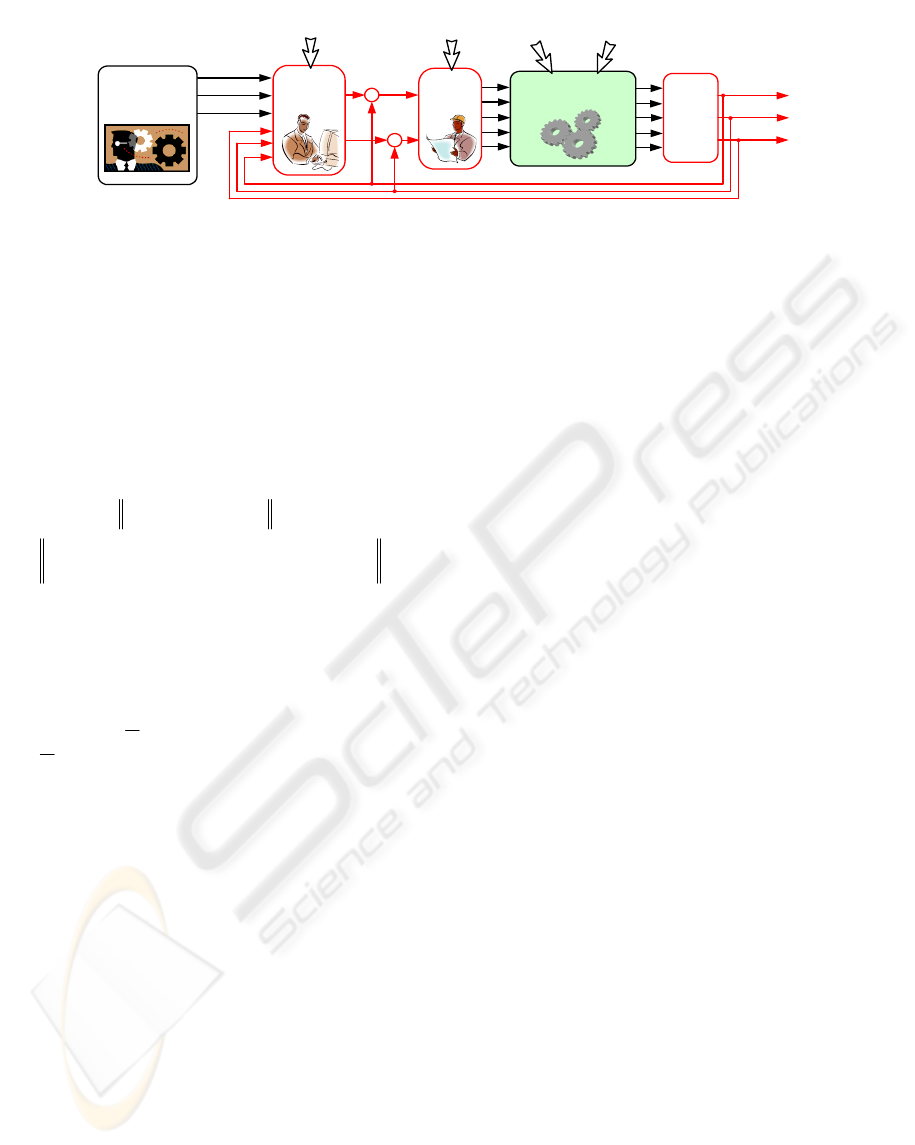
this paper as “production KPIs” (see Figure 1).

179

Zorzut S., Žnidarši

c A. and Jovan V. (2006).

KEY PERFORMANCE INDICATORS IN PLANT-WIDE CONTROL.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 179-182

DOI: 10.5220/0001201301790182

 SciTePress

This production control problem can be

mathematically formulated as in (Stephanopoulos

and Ng, 2000):

Let z

PROFIT

represents the operating profit:

. costs production

costs materialraw luesproduct vaz

PROFIT

∑

∑∑

−

−−=

The feedback-based solution leads to the

following optimisation problem:

),,(z),,(zmin

zzMinimize

PROFITPROFIT

C(.)sp,,y,u

PROFITspPROFIT,

fbfb

dyudyu −

=−

subject to

).(

esdisturbanc process

sconstraint process 0 ) , ,(

dynamicsplant ) , ,(

fbfb

yCu

dyug

dyuhy

≤≤

∈

≤

where, u

and y

denote the manipulations and

measurements involved in the feedback-based

solution and C is the structure of the entire

production control system.

3 THE CASE STUDY

The polymer emulsion batch production process

taken in this paper for the case study is a typical

representative of process-oriented production where

production effectiveness to a great extent relies on

the quality of the production control system. The

process is described in more details in (Jovan and

Zorzut, 2006).

A procedural model of the case study

production process has been developed to facilitate

experimenting and the verification of the closed-

loop control structure. The model was designed in

the academically established Matlab, Simulink and

Stateflow simulation environments. The simulated

data are stored in the MS Access database and are

available for different on-line or off-line processing.

Given the final objective of stabilising the

existing production process, a promising idea is to

introduce a closed-loop production management

concept so that specific production KPIs serve as the

reference values for the closed loop production

control system. It is hypothesised that such an

approach can contribute to more stable production

and better final product uniformity and quality.

Three production KPIs were chosen to characterise

the case study production process:

• Productivity (also denoted as actual production

rate or production yield). Productivity is defined for

the described production process as the amount of

all products that were produced over a set

production period. All batches finished within the

set time window (production period) are taken into

account and the average amount of products

produced in an hour is calculated.

• Mean Product Quality. The Mean Quality KPI is

calculated as the mean value of the quality factors

for the batches completed in the set time window.

• Mean Production Costs. Production costs consist

of raw material costs, energy costs, other operating

costs and fixed costs in the set time window. The

mean production costs are calculated as the sum of

all production costs within a time window, divided

by the amount of all products produced in this time

window.

These three KPIs represent the output

(controlled) variables on Figure 1. Maintaining the

predefined set points for these KPIs is achieved by

properly adjusting the manipulated (input) variables,

which are in this case: Raw Material Quality,

Production Speed and Batch Schedule. Determining

the influence of the input variables and disturbances

on the output variables (selected KPIs) is essential

for efficient production control.

PRODUCTION

PROCESSES

Energy and

raw materials

Disturbances

WHAT

HOW MUCH

WHEN

Productivity

Quality

Costs

MANAGEMENT

LEVEL

Technological

constraints

Economic

issues

Production

manager

using DSS

Operator

using

DSS

Key

Performance

Indicators

Figure 1: Closed-Loop Control Structure of the Production Process.

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

180

3.1 Simulation Runs

To see how the production speed and the quality of

raw materials affect productivity, product quality

and production costs, a simulation run was

performed. Simulation run was divided in three

phases, where the production speed was changed

from low to normal and finally to high. On Figure 2

the first phase lasts from 0 to 450 hours of

simulation time, the second phase from 450 to 870

hours and the third phase from 870 till the end. In

each phase the quality of the raw materials was

subsequently increased from low to very high (0.85

to 1.1). The KPIs for Product Quality, Productivity

and Production Costs were observed. The KPIs were

evaluated every 12 hours for the time window of 120

hours.

Figure 2 represents the response of the Product

Quality KPI. In the first phase of the simulation run

the production speed was low, which represents the

best working conditions in the production process.

Over the simulation run the quality of raw materials

gradually increased and the influence of this change

on the Product Quality KPI can be observed. As

expected, better quality raw materials contribute to

better quality final products.

In the second phase of the simulation run the

production speed is increased, which usually leads to

decreasing production process quality. Raw material

quality changed in the same manner as in the

previous phase: from low to high. The Product

Quality KPI first decreased and when it reached the

bottom it started increasing as in the first phase. The

change in product quality is momentary but the

change in the Product Quality KPI is gradual. The

KPI evaluation algorithm averages the product

quality in the set time window, which can be seen in

this section of the figure. The second interesting

phenomenon is the influence of production process

quality on product quality. The mean quality of the

products decreases by about 10 %. In the third phase

the pattern is repeated.

Figure 3 represents the Productivity KPI for the

same simulation run. The Productivity KPI has

slightly increasing trend with higher production

speed. At the beginning of the third phase of the

simulation run high production speed causes the

significant decrease of productivity. This is the

result of coincidence that the quality of the

production process and also the quality of the raw

materials are low. Consequently, some batches do

not attain prescribed quality requirements and they

have to be recycled, what affects Productivity KPI.

The appearance of off-spec batches can be noticed

0 200 400 600 800 1000 1200

0.5

1.5

Raw materials quality and production rate

Raw materials quality

Production rate

0 200 400 600 800 1000 1200

0.5

1.5

Mean product quality for the time window: 120h

Prod uc tion time(h)

Mean product quality

Figure 2: Response of the Mean Product Quality KPI to

Raw Material Quality and Production Speed.

0 200 400 600 800 1000 1200

0.5

1.5

Raw materials quality and production speed

Raw materials quality

Production speed

0 200 400 600 800 1000 1200

200

400

600

800

1000

1200

1400

1600

Produc tiv ity for the time window: 120h

Production time(h)

/h)

Figure 3: Response of the Productivity KPI to Raw

Material Quality and Production Speed.

on the Figure 3 (time period from 900 to 950 hours)

where the reactor occupancy for some batches is

increased due to the need of recycling of bad batches

entering in the production process.

Figure 4 represents the mean Production Costs

KPI. The production costs per product unit increase

with the increasing quality of raw materials. There is

a slight increase in costs with increasing production

speed.

The following simulation run presents the open-

loop control of the Product Quality KPI.

0 200 400 600 800 1000 1200

0.5

1.5

Raw materials quality and production rate

Raw materia ls quality

Production rate

0 200 400 600 800 1000 1200

100

150

200

Mean product cost for the time window: 120h

Production time(h)

ean pro

cos

(Sit/k

)

Figure 4: Response of the Mean Production Costs KPI to

Raw Material Quality and Production Speed

KEY PERFORMANCE INDICATORS IN PLANT-WIDE CONTROL

181

0 50 100 150 200 250 300 350 400

0.5

1.5

Raw materials quality and production speed

Raw materia ls quality

Production speed

0 50 100 150 200 250 300 350 400

0.2

0.4

0.6

0.8

1.2

Mean product quality for the time window: 75h

Production time (h)

Mean product quality

Figure 5: Open-Loop Control of the Product Quality KPI.

The experiment represents the execution of a normal

schedule of production jobs using raw materials with

normal quality at normal production speed. After a

certain time period, a disturbance occurs in the form

of a decrease in the quality of raw materials, which

is reflected in the considerable decreased value of

the mean of the Product Quality KPI (see Figure 5).

As an open-loop control action the production

manager then slows down current production speed.

The quality of both the production process and final

product gradually increase, and consequently this is

reflected in the increase in the mean value of the

Product Quality KPI. This is not the only possible

action that production manager could take, but in the

presented case it was sufficient to eliminate the

disturbance.

4 CONCLUSIONS

The ideal plant-wide control system should ensure

that the production process is constantly working in

an optimal manner. As a result of the plant-wide

focus, a plant-wide control problem possesses

certain characteristics that are not encountered in the

design of control systems for single units, such as

the following (Stephanopoulos and Ng, 2000): (a)

the variables to be controlled by a plant-wide control

system are not as clearly or as easily defined as for

single units; (b) local control decisions, made within

the context of single units, may have long-range

effects throughout the plant; (c) the size of the plant-

wide control problem is significantly larger than that

for the individual units, making its solution

considerably more difficult.

This paper proposes an approach to measuring

and presenting the attainment of production

objectives in the form of production KPIs. With this

approach the implicit production objectives were

translated into measurable values that can be

extracted from existing production data. In this way

the production control concept and the role of a

production manager are slightly changed; instead of

monitoring and controlling several tens and

hundreds of process variables at a low production

level, a production manager monitors and controls

only a few major production KPIs with the aim of

achieving the most important implicit production

objectives, e.g. high product quality, high

productivity and minimal production costs.

The procedural model of the case study

production process has been developed and used in a

number of simulation runs. The preliminary

simulation results presented indicate that this work

could evolve towards the implementation of a

production KPI-based control system in a real

industrial plant. The intention in future is to improve

the existing production process model, validate it

rigorously and incorporate it into a Decision Support

System for production control in the polymerisation

plant that was used as the case study production

process in this paper.

REFERENCES

DeBusk, G. K., Brown, R. M., Killough, L. N. (2003):

Components and relative weights in utilization of

dashboard measurement systems like the Balanced

Scorecard, The British Accounting Review, Volume

35, Issue 3, pp. 215-231.

Jovan, V. and Zorzut, S. (2006): Use of Key Performance

Indicators in Production Management, Proceedings of

the IEEE International Conference on Cybernetics

and Intelligent Systems, 7.-9. June, Bangkok, 2006.

Lohman, C., Fortuin, L., Wouters, M. (2004): Designing a

performance measurement system: A case study,

European Journal of Operational Research 156,

Elsevier press, pp. 267-286.

Rakar, A., Zorzut, S., Jovan, V. (2004): Assesment of

production performance by means of KPI,

Proceedings of the Control 2004, 6-9 September,

2004, University of Bath, UK.

Skogestad S. (2004): Control structure design for complete

chemical plants, Computers and Chemical

Engineering 28, pp. 219-234.

Stephanopoulos G., Ng C. (2000): Perspectives on the

synthesis of plant-wide control structures, Journal of

Process Control 10 (2000), pp 97-111.

Vicens, E., Alemany M. E., Andres C., Guarch J. J.

(2001): A design and application methodology for

hierarchical production planning decision support

system in an enterprise integration context, Int.

Journal of Production Economics 74, Elsevier Press,

pp. 5-20.

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

182