
PARTIAL STABILIZABILITY OF CASCADED SYSTEMS
APPLICATIONS TO PARTIAL ATTITUDE CONTROL
Chaker Jammazi
Laboratoire d’Ing
´
eni
´
erie Math
´
ematique
Ecole Polytechnique de Tunisie. Tunisie
Azgal Abichou
Laboratoire d’Ing
´
eni
´
erie Math
´
ematique
Ecole Polytechnique de Tunisie. Tunisie
Keywords:
Brockett’s Condition, Partial stabilization, Backstepping, Partial Attitude Control.
Abstract:
In this work, the problem of partial stabilization of nonlinear control cascade systems with integrators is con-
sidered. The latter systems present an anomaly, which is the non complete stabilization via continuous pure-
state feedback, this is due to Brockett necessary condition. To cope with this difficulty we propose the partial
stabilization. For a given motion of a dynamical system, say x(t, x
0
, t
0
) = (y(t, y
0
, t
0
), z(t, z
0
, t
0
)),
the partial stabilization is the qualitative behavior of the y-component of the motion (i.e the asymptotic
stabilization of the motion with respect to y) and the z-component converges, relative to the initial vector
x(t
0
) = x
0
= (y
0
, z
0
). In the present work, we establish a new results for the adding integrators for partial
stabilization, we show that if the control systems is partially stabilizable, then the augmented cascade system
is partially stabilizable. Two applications are considered. The first one is devoted to partial attitude stabiliza-
tion of rigid spacecraft. The second application is intended to the study of underactuated ship. Numerical
simulations are given to illustrate our results.
1 INTRODUCTION
Control problems involving cascaded systems have
attracted considerable attention in the past years. Un-
fortunately many controllable cascaded systems can
not stabilizable by pure state feedback laws this is
due to Brockett (Brockett, 1983) necessary condition.
Several solutions to overcome the limitation imposed
by Brockett condition have been presented in the liter-
ature knowing for example the time-varying method
developed by Morin (Morin et al., 1994). The con-
ception of time-varying feedback laws is an impor-
tant method to solving the stabilization problem, nev-
ertheless, the fact to introduce the time in these feed-
back laws product a oscillation of the system around
his point of equilibrium see for instance Pettersen and
Egeland (Pettersen and Egeland, 1996), (Morin et al.,
1994), (Beji et al., 2004), Pettersen and Nijmeijer (Pe-
tersen and Nijmeijer, 2001).
In this paper, we propose the partial stabilization by
smoothly state feedback laws. Partial stabilizability,
is the asymptotic stability with respect to most of the
system’s state, and the rest converges to same position
which depend to initial conditions.
The aim of the paper is to extend the well known
backstepping theorem to the case of partial stabiliz-
ability of nonlinear control systems. We have shown
that if the original system is partially stabilizable then
the cascade systems with integrators inherits the same
property, to this end we have developed the inver-
sion Lyapunov theorem for the stability with respect
to part. The theoretical result is applied to solving
two problems: The first is the partial stabilization of
the rigid spacecraft with two controls, where we have
improve the Zuyev’s (Zuyev, 2001) result that the ve-
locity ω
3
of the third axes converges by using smooth
state feedback laws. The second problem treated is
the attitude of underactuated ship, we have construct
two smooth feedback laws that stabilize asymptoti-
cally five components and the sixth converges.
A numerical simulations are given to valid our re-
sults.
The paper is structured as follows: The next sec-
tion deals with some mathematical preliminaries. In
particular, the inversion of the Lyapunov theorem of
the stability with respect to part is demonstrated. The
backstepping techniques and partial stabilizability is
treated in section 3. In section 4 we give two appli-
cations for the backstepping result. Issues left for the
future investigation are discussed in the conclusions.
296
Jammazi C. and Abichou A. (2006).
PARTIAL STABILIZABILITY OF CASCADED SYSTEMS APPLICATIONS TO PARTIAL ATTITUDE CONTROL.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 296-301
DOI: 10.5220/0001205802960301
Copyright
c
SciTePress

2 PRELIMINARIES
In this section the concept of partial stability and par-
tial stabilizability and some of its results will be re-
viewed in order to build the mathematical background
for the stability proofs in the subsequent sections.
We consider the dynamical systems in finite dimen-
sion of the following form:
˙x
1
= f
1
(x
1
, x
2
)
˙x
2
= f
2
(x
1
, x
2
).
(1)
here f = (f
1
, f
2
) is supposed to be in class
C
∞
(R
n
× R
m
), x
1
∈ R
p
, x
2
∈ R
n−p
and p in-
teger such that 0 < p ≤ n. We suppose that
f
1
(0, x
2
) = 0, ∀x
2
∈ R
n−p
f
2
(0, 0) = 0 (2)
Definition 1 (Partial Stability) The system (1) is
said to be partially stable if the two following con-
ditions a), b) are satisfied:
(a)
∀ ǫ > 0, ∃η > 0 s.t.|x
1
(0)| + |x
2
(0)| < η
⇒ |x
1
(t)| + |x
2
(t)| < ǫ, ∀ t ≥ 0.
(3)
(b)
∃ r > 0 : |x
1
(0)| + |x
2
(0)| ≤ r :
⇒
x
1
(t) → 0, t → +∞.
x
2
(t) → α, t → +∞
(4)
which α depends in (x
1
(0), x
2
(0)) only.
We consider the nonlinear control systems of
the following form
˙x
1
= f
1
(x
1
, x
2
, u)
˙x
2
= f
2
(x
1
, x
2
, u)
(5)
where x = (x
1
, x
2
) ∈ R
n
is the state, and u(t) ∈
R
m
is the control, x
1
∈ R
p
,x
2
∈ R
n−p
,0 < p ≤ n
Definition 2 (Partial Stabilizability) The system (5)
is said to be partially stabilizable if there exists a con-
tinuous function φ : R
p
× R
n−p
−→ R
m
, such that
φ(0, x
2
) = 0 and the system in the closed-loop:
˙x
1
= f
1
(x
1
, x
2
, φ(x
1
, x
2
))
˙x
2
= f
2
(x
1
, x
2
, φ(x
1
, x
2
))
(6)
is partially stable in the sense of definition 1.
Thanks to recent contribution of (Lin et al., 1995), in
the dynamic given ˙x
2
= f
2
(x
1
, x
2
), we considered
x
2
as a parameter, with the assumption (2) and with
a result due to Lin (Lin et al., 1995), we announce
the following theorem, which gives a converse Lya-
punov theorem for the stabilization with respect to
part of variables, this result extend the Kurzweil the-
orem (Rouche et al., 1977).
Theorem 1: We assume that the system (1) is par-
tially stable with respect to x
1
, then there exists a
smooth function V : R
p
× R
n−p
→ R such that
(i) V is positive definite with respect to x
1
(ii)
˙
V (x
1
, x
2
) is definite negative with respect to x
1
.
Proof: We suppose that the system (1) is partially sta-
ble, then by definition of partial stability, the system
(1) is stable and by Persidski theorem (Rouche et al.,
1977), there exist a positive definite function V
1
such
that
˙
V
1
≤ 0. By hypothesis we have f
1
(0, x
2
) = 0,
then in the dynamic of ˙x
1
= f
1
(x
1
, x
2
) we can sup-
pose that x
2
is a parameter, then by Lin (Lin et al.,
1995) result, see also Rouche (Rouche et al., 1977)
this system admits a smooth Lyapunov function V
2
with respect to a closed, invariant set A = {0}. Thus
we have V
2
: R
p
× R
n−p
→ R satisfying:
a) there exist two K
∞
-functions α
1
and α
2
such that
α
1
(|x
1
|
A
) ≤ V
2
(x
1
, x
2
) ≤ α
2
(|x
1
|
A
),
b) there exists a continues, positive definite function
α
3
such that
˙
V
2
(x
1
, x
2
) ≤ −α
3
(|x
1
|
A
)
here |x
1
|
A
= d(x
1
, A) = d(x
1
, 0) = |x
1
|.
We consider then the Lyapunov function defined by
V (x
1
, x
2
) = V
1
(x
1
, x
2
) + V
2
(x
1
, x
2
),
the candidate function V satisfies the propriety (i) and
(ii).
3 PARTIAL STABILIZABILITY
AND BACKSTEPPING
In this section, we give an extension of the
well known backstepping techniques of Coron-Praly
(Coron and Praly, 1991) to partial stabilizability the-
ory.
Theorem 2: We suppose that:
˙x
1
= f
1
(x
1
, x
2
, u)
˙x
2
= f
2
(x
1
, x
2
, u)
(7)
is partially stabilizable by static state feedback of
C
r
, r ≥ 1. Then the augmented cascaded systems
with integrators
(
˙x
1
= f
1
(x
1
, x
2
, y)
˙x
2
= f
2
(x
1
, x
2
, y)
˙y = u
(8)
(i) is Lyapunov stable.
(ii) is asymptotic stabilizable with respect to (x
1
, y) by
static preliminary feedback u
0
(x
1
, x
2
, y) of C
r−1
(iii) there exists a scalar function ψ ∈ C
0
(R
n+m
) sat-
isfying:
ψ(x, y) > 0, x = (x
1
, x
2
) (9)
PARTIAL STABILIZABILITY OF CASCADED SYSTEMS APPLICATIONS TO PARTIAL ATTITUDE CONTROL
297

such that with the state feedback control
u(x, y) =
u
0
, if |y − φ(x)| = 0,
u
0
− (y − φ(x))ψ(x, y), if |y − φ(x)| 6= 0
(10)
the solution x
2
(t) converges to a constant vector
a(x(0), y(0)).
Proof: Assume that the system (7) is partially stabi-
lizable by a state feedback of C
r
, then from definition
2 there exists a C
r
map φ : R
p
× R
n−p
−→ R
m
φ(0, x
2
) = 0, ∀ x
2
∈ R
n−p
such that the system on
closed-loop
˙x
1
= f
1
(x
1
, x
2
, φ(x
1
, x
2
))
˙x
2
= f
2
(x
1
, x
2
, φ(x
1
, x
2
))
(11)
is partially stable.
Theorem 1 yields the existence of a smooth Lyapunov
function V for the closed-loop system (7) such that
V (x
1
, x
2
) is positive definite and
˙
V (x
1
, x
2
) =
∂V
∂x
1
f
1
(x) +
∂V
∂x
2
f
2
(x) < 0, ∀x
1
6= 0
(12)
Let
W (x
1
, x
2
, y) := V (x
1
, x
2
) +
1
2
|y − φ(x
1
, x
2
)|
2
.
We derive W along a trajectory of system (8), we ob-
tain with the preliminary feedback
u
0
(x, y) =
∂φ
∂x
1
f
1
(x, y) +
∂φ
∂x
2
f
2
(x, y)
− G
T
1
(x, φ(x))
∂V
∂x
1
− G
T
2
(x, φ(x))
∂V
∂x
2
+ φ(x) − y.
∀(x, y) ∈ R
n
× R
m
˙
W (x, y) =
˙
V (x) − |y − φ(x)|
2
(13)
we use (12) and (13) we obtain:
˙
W (x, y) = 0 ⇔ (x
1
, y) = (0, φ(0, x
2
)) = (0, 0)
Then W is a candidate Lyapunov function, we con-
clude by Risito-Rumyantsev’s theorem (Vorotnikov,
1998) that (x
1
, y) = (0, 0) is asymptotically stable,
then (i) and (ii) are shown.
Convergence of x
2
:
Let the functional defined by
T (x, y, t) = W (x, y) +
Z
t
0
|f
2
(x, y)(s)| ds (14)
We have T (x, y, t) ≥ 0. We drive T a long a trajec-
tory of system (8) with the new feedback law u given
by (10) we obtain:
˙
T (x, y, t) =
˙
V (x) − |y − φ(x)|
2
− |y − φ(x)|
2
ψ(x, y)
+ |f
2
(x, y)|
(15)
to have
˙
T ≤ 0, it’s sufficient to have
˙
V (x) − |y − φ(x)|
2
+ |f
2
(x, y)|
≤ |y − φ(x)|
2
ψ(x, y)
(16)
two cases are presented.
Case 1: |y − φ(x)| = 0
In this case all ψ(x, y) > 0 is appropriate. We have
y = φ(x)
the sub-manifold {
˙
W = 0} is reduced to {(0, x
2
, 0)}
and the system (8) is asymptotically stabilizable with
respect to (x
1
, y).
The component x
2
satisfies the ordinary differential
equation
˙x
2
= f
2
(x
1
, x
2
, φ(x))
x
2
converges by hypothesis (because (x
1
, x
2
) is so-
lution of the system (7)).
Case 2: |y − φ(x)| 6= 0.
Because ψ(x, y) > 0, the inequality (16) becomes
˙
V (x) − |y − φ(x)|
2
+ |f
2
(x, y)|
|y − φ(x)|
2
≤ ψ(x, y) (17)
with (17), we can choose ( e
x
≥ x, ∀x ∈ R)
ψ(x, y) = exp(
˙
V (x) − |y − φ(x)|
2
+ |f
2
(x, y)|
|y − φ(x)|
2
)
(18)
since with (14), (16) and (18) we have
˙
T ≤ 0, then T
is a positive decreasing function with respect to time
t, we conclude that has a finite limit
lim
t→+∞
T (x, y, t) = T
∞
.
This implies that the integral
Z
+∞
0
|f
2
(x
1
, x
2
, y)(s)| ds < +∞
4 APPLICATIONS
4.1 Partial Stabilization of Rigid
Spacecraft with Two Controls
The problem of attitude stabilization of a rotating
rigid body with two controls has already been stud-
ied extensively in the literature.
A means importing to get round the obstruction of
Brockett is to conceive instationnary feedback laws.
Nevertheless, the fact to introduce the time in these
laws can produce oscillations of the system around
its point of equilibrium (see for instance, Morin et al
(Morin et al., 1994)). To surmount these difficulties,
we present a partial stabilizability method to solve the
partial attitude stabilization with smooth controls with
ICINCO 2006 - ROBOTICS AND AUTOMATION
298

respect to the state only.
In this work we will improve Zuyev’s (Zuyev, 2001)
result, and we prove that the velocity ω
3
converges.
Equation of motion
We consider the Euler-Poisson parameterization see
Tsiotras (Tsiotras, 1996), or Zuyev (Zuyev, 2001)
which describe the motion of the rigid-body, it is writ-
ten in the following form:
˙ω
1
= u
1
˙ω
2
= u
2
˙ω
3
= ω
1
ω
2
˙ν
1
= ω
3
ν
2
− ω
2
ν
3
˙ν
2
= ω
1
ν
3
− ω
3
ν
1
˙ν
3
= ω
2
ν
1
− ω
1
ν
2
.
(19)
We will be interested to stabilize partially the equilib-
rium ω
1
= ω
2
= ω
3
= 0, ν
1
= ν
2
= 0, ν
3
= 1.
We notice that ˙ν
1
ν
1
+ ˙ν
2
ν
2
+ ˙ν
3
ν
3
= 0, then
ν
2
1
+ ν
2
2
+ ν
2
3
=constant. Then we can suppose that:
ν
2
1
+ ν
2
2
+ ν
2
3
= 1
We choose, on the hemisphere ν
3
> 0, the equality
ν
2
1
+ ν
2
2
+ ν
2
3
= 1, which implies:
ν
3
=
q
1 − (ν
2
1
+ ν
2
2
).
To simplify our task we use the theorem 2. It’s easy to
show that the reduced system of (19) is locally equiv-
alent to the system given by:
˙ω
3
= u
1
u
2
˙ν
1
= −u
2
− u
2
g(ν
1
, ν
2
) + ω
3
ν
2
˙ν
2
= u
1
+ u
1
g(ν
1
, ν
2
) − ω
3
ν
1
˙ν
3
= u
2
ν
1
− u
1
ν
2
(20)
where g is smooth fonction satisfies g(0, 0) =
g
′
(ν
1
, ν
2
)(0, 0) = 0.
Proposition 1: Let α > 0, we choose the feedbacks
u
1
and u
2
in this manner:
u
1
= −α ν
2
+ ν
2
ω
3
, u
2
= α ν
1
− ν
1
ω
3
.
Then
i) The system (20) is stable with respect to
(ν
1
, ν
2
, ν
3
, ω
3
).
ii) The system (20) is exponentially stable with re-
spect to (ν
1
, ν
2
).
iii) The angular velocity ω
3
converges.
iv) The point ν
3
converges to 1.
Proof: In closed loop the system (20) can be writhen
in Lyapunov-Malkin form (Zenkov et al., 2002). We
have:
˙ω
3
˙ν
3
= S(ν
1
, ν
2
, ν
3
, ω
3
)
˙ν
1
˙ν
2
=
−α 0
0 −α
ν
1
ν
2
+ R(ν
1
, ν
2
, ν
3
, ω
3
)
The matrix
−α 0
0 −α
has −α < 0 as eigenvalues. Besides the functions
R(ν
1
, ν
2
, ν
3
, ω
3
) and S(ν
1
, ν
2
, ν
3
, ω
3
) have a nonlin-
ear terms and vanishing together at (0, 0, 0, ω
3
) and
at (0, 0, 0, 0).
The Lyapunov-Malkin theorem and the center mani-
fold theory allow us to conclude (i), (ii) and (iii).
By using the fact that ν
3
> 0 and the relation
ν
2
1
+ ν
2
2
+ ν
2
3
= 1 to conclude lim
t→+∞
ν
3
= 1.
In this proposition we give the feedback con-
troller that achieve the partial stabilization of the
system (19).
Proposition 2: The feedback controller that ensure
the partial stabilisability of the system (19) are given
by:
φ
1
(x) = −k(ω
1
− u
1
(x))
φ
2
(x) = −k(ω
2
− u
2
(x))
(21)
u
1
(x) and u
2
(x) are given in the proposition 1; with
k is large enough and x = (ω
i
, ν
i
), i = 1, 2, 3.
Proof: We note that the system (20) its homoge-
neous of degree 0 with respect to dilation δ
λ
(x) =
(λν
1
, λν
2
, λ
2
ν
3
), then we use the result due to Morin
et al (Morin and Samson, 1996) to conclude the as-
ymptotic stability of the system (19) with respect to
(ω
1
, ω
2
, ν
1
, ν
2
, ν
3
). By using the proposition 1 (ii),
we conclude that there exists k
1
, k
2
, C > 0 such that
|u
1
(x)| ≤ C e
−k
2
t
, |u
2
(x)| ≤ C e
−k
1
t
(22)
then it’s easy to conclude that
ω
1
∈ L
2
[0, +∞), ω
2
∈ L
2
[0, +∞) (23)
Thus with ˙ω
3
= ω
1
ω
2
and the Cauchy-Schwarz in-
equality to conclude that
˙ω
3
∈ L
1
[0, +∞)
which prove that ω
3
converges.
4.2 Partial Stabilization of the Ship
This subsection is devoted to the study the underactu-
ated ship, it was shown by Pettersen and Egeland (Pet-
tersen and Egeland, 1996) that no continues or dis-
continues static-state feedback law exist which make
the origin of the ship system asymptotically stable.
Our treatment enable us to overcome the difficulties
imposed by the Brockett condition. The stabilization
problem for the under-actuated ship in treated in the
sense partial stabilization.
One of the most difficult operations of the captain of
the ship, it is to put the boat on the quay. In this work
we develop a smoothly feedback controls, that assure
PARTIAL STABILIZABILITY OF CASCADED SYSTEMS APPLICATIONS TO PARTIAL ATTITUDE CONTROL
299

the locally convergence of the ship on the quay.
Equation of Motion: The ship see Pettersen-
Nijmeijer (Petersen and Nijmeijer, 2001) can be
model by the simplified one
˙x
1
= u
1
˙x
2
= −c x
1
x
3
− x
2
˙x
3
= u
2
˙
θ = x
1
cosψ − x
2
sinψ
˙
φ = x
1
sinψ + x
2
cosψ
˙
ψ = x
3
(24)
x
1
, x
2
, x
3
are the velocities in surge, sway and yaw
respectively and θ, φ, ψ denote the position and ori-
entation of the ship in the earth frame. u
1
and u
2
are
the controls. The reel c > 0. The system (24) is pre-
sented in cascaded form, to study the partial stabiliz-
ability of (24), we applied the theorem 2. The reduced
system of (24) is in the following form:
˙x
2
= −c u
1
u
2
− x
2
˙
θ = u
1
cosψ − x
2
sinψ
˙
φ = u
1
sinψ + x
2
cosψ
˙
ψ = u
2
(25)
Theorem 3: With the feedback control given by
v
1
= −µ
1
(x
1
− u
1
(x))
v
2
= −µ
2
(x
3
− u
2
(x))
(26)
where µ
i
> 0 is large enough, u
1
(x) and u
2
(x) are
given by
u
1
: = −k
1
θ + x
2
ψ
u
2
: = −k
2
ψ.
(27)
where k
1
, k
2
are large strictly positively. The sys-
tem (24) is partially stabilizable in the sense that
(x
1
, x
2
, x
3
, θ, ψ) = (0, 0, 0, 0) is asymptotically
stable and φ converges.
5 NUMERICAL SIMULATIONS
5.1 Simulations of Rigid Spacecraft
In this subsection we present a numerical simula-
tions to valid our results with the feedback controls
φ
1
(x) = −10(ω
1
− u
1
(x)), φ
2
(x) = −10(ω
2
−
u
2
(x)), x = (ω
i
, ν
i
) where u
1
= 10ν
2
+ ν
2
ω
3
,
u
2
= 10ν
1
− ν
1
ω
3
The results are shown in Fig. 1-
3. These simulations show that the proposed controls
laws partially asymptotically stabilizable the system
given by equations (19).
5.2 Simulations of Underactuated
Ship
In this subsection, we take the feedback controls v
1
=
−µ
1
(x
1
− u
1
(x)), v
2
= −µ
2
(x
3
− u
2
(x)) with µ
1
=
µ
2
= 10 and u
1
= −5θ + x
2
ψ, u
2
= −5ψ
0 2 4 6 8 10 12 14 16 18 20
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
time (s)
ν
2
ν
1
Figure 1: Comportment of ν
1
, ν
2
.
0 2 4 6 8 10 12 14 16 18 20
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
time (s)
ν
3
Figure 2: Comportment of ν
3
.
6 CONCLUSION
The problem of partial stabilization by means of
smoothly time-invariant feedback laws has been con-
sidered in the paper. Our treatment enables us to over-
come the difficulties imposed by Brockett’s condition.
The main result shown that the backstepping tech-
niques can be extended to partial asymptotic stabil-
ity for nonlinear control systems, and that this theo-
rem can be used for solving the partial stabilization
of many control systems. The first problem treated in
this paper is the attitude control of rigid spacecraft, in
this sense we have improve the Zuyev’s result and we
have shown that the velocity ω
3
of the 3
th
axes con-
verges.
The second problem treated is the partial stabiliza-
tion of under-actuated ship, by using the backstep-
ping techniques we synthesized a smooth feedback
controls to make the axes φ of the ship in the earth-
fixed frame converges. This theoretical is desirable in
many practical situation, indeed, the feedback control
developed here make easy (for the captain) to put the
ship on the quay.
The future work is to extend the backstepping tech-
ICINCO 2006 - ROBOTICS AND AUTOMATION
300
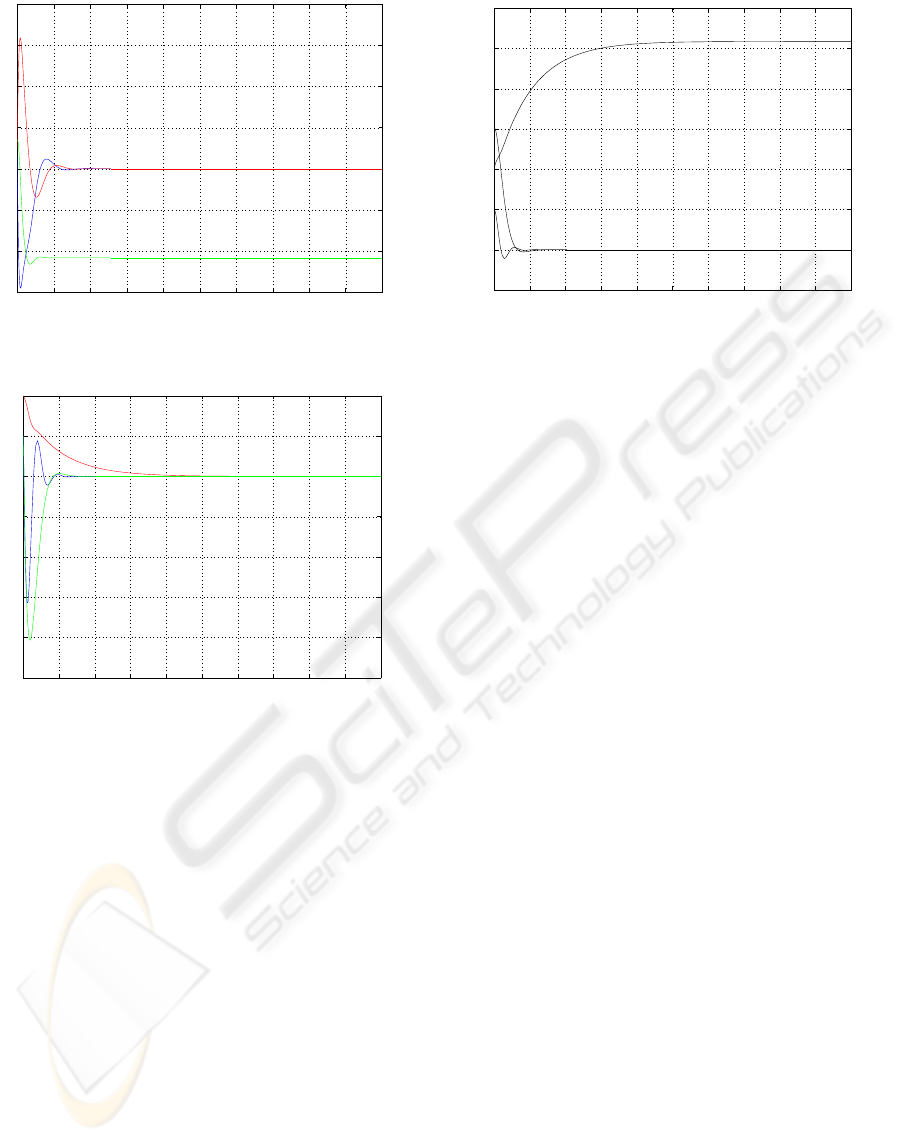
0 2 4 6 8 10 12 14 16 18 20
−3
−2
−1
0
1
2
3
4
time (s)
ω
1
ω
3
ω
2
Figure 3: Comportment of the angular velocity of
ω
1
, ω
2
, ω
3
.
0 1 2 3 4 5 6 7 8 9 10
−1
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
time (s)
x
1
x
3
x
2
Figure 4: Comportment of the velocity x
1
, x
2
, x
3
.
niques for the partial stabilizability by bounded feed-
back laws, and to applied it to construct a bounded
feedback laws to assure the partial stabilization of the
satellite (respectively of the under-actuated ship).
ACKNOWLEDGEMENTS
The first author would like to thank Professor Jean-
Michel Coron for several interesting discussions and
helpful comments.
REFERENCES
Beji, L., Abichou, A., and Bestaoui, Y. (2004). Position
and attitude control of an underactuated autonomous
airship. International journal of differential equations
and applications, 8(3).
Brockett, R. W. (1983). Asymptotic stability and feedback
0 1 2 3 4 5 6 7 8 9 10
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
time (s)
φ
θ
ψ
Figure 5: Positions of the axes θ, φ, ψ.
stabilization. Differential geometric control theory,
Progress in Math., 27:181–191.
Coron, J.-M. and Praly, L. (1991). Adding an integrator for
the stabilization problem. Systems and control letters,
17:89–104.
Lin, Y., Sontag, E. D., and Wang, Y. (1995). Input to state
stabilizability for parameterized families of systems.
Intern. J. Robust and Nonlinear Control, 5:187–205.
Morin, P. and Samson, C. (1996). Application of back-
stepping techniques to the time-varying exponential
stabilization of chained form systems. Rapport de
recherche N 2792, INRIA Sophia Antipolis.
Morin, P., Samson, C., Pomet, J.-B., and Jiang, Z.-P. (1994).
Time-varying feedback stabilization of the attitude
of a rigid spacecraft with two controls. Rapport de
recherche, INRIA Sophia Antipolis.
Petersen, K. Y. and Nijmeijer, H. (2001). Underactuated
ship tracking control: theory and expriments. Int. J.
Control, 74(14):1435–1446.
Pettersen, K. Y. and Egeland, O. (1996). Exponential sta-
bilization of an underactuated surface vessel. Proc. of
the 35th IEEE Conference on Decision and Control,
pages 967–971.
Rouche, N., Habets, P., and Laloy, P. (1977). Stability the-
ory by lyapunov’s direct method. Applied mathemati-
cal sciences, springer edition.
Tsiotras, P. (1996). On the choice of coordinates for control
problems on so(3). 30th Annual Conference on Infor-
mation Sciences and Systems, Princeton University.
Vorotnikov, V. I. (1998). Partial Stability and Control.
Birkhuser.
Zenkov, D., Bloch, A., and Marsden, J. (2002). The
lyapunov-malkin theorem and stabilization of the uni-
cycle with rider. Systems and control letters, 45:293–
302.
Zuyev, A. L. (2001). On partial stabilization of nonlinear
autonomous systems: Sufficient conditions and ex-
amples. Proc. of the European Control Conference
ECC01. Porto (Portugal).
PARTIAL STABILIZABILITY OF CASCADED SYSTEMS APPLICATIONS TO PARTIAL ATTITUDE CONTROL
301
