
DESIGN OF AN ITERATIVE LEARNING CONTROL FOR A SERVO
SYTEM USING MULTI-DICTIONARY MATCHING PURSUIT
Iuliana Rotariu
ARC Centre of Excellence for Autonomous Systems, University of Sydney
NSW2006, Sydney, Australia
Erik Vullings
MELCOE, Macquarie University
NSW2109, Sydney, Australia
Keywords:
Iterative Learning Control, System Dynamics, Mechatronics, Time-frequency analysis, Wigner distribution,
Atomic decomposition, Matching Pursuit.
Abstract:
Many motion systems repeatedly follow the same trajectory. However, in many cases, the motion system does
not learn from tracking errors obtained in a previous cycle. Iterative Learning Control (ILC) resolves this
issue by compensating for previous tracking errors, but it suffers from not being able to distinguish between
tracking errors caused by machine dynamics versus errors caused by noise, and by trying to ’learn’ the noise,
additional errors are introduced.
In this paper we address this issue by using the servo error signal by identifying the time-varying nonlinear
effects, which can be learned and therefore improve the position accuracy, versus the stochastic effects, which
cannot be learned. The identification of these effects is performed by means of time-frequency analysis of
the servo error and therefore our goal is to obtain a high-resolution time-frequency energy distribution of the
analyzed signal. Here we compare the servo error energy distribution by three means: (1) Wigner distribution;
(2) adaptive signal decomposition over one dictionary of modulated versions of wavelets (simple atomic dic-
tionary); (3) and by means of combining several simple atomic dictionaries into a complex atomic dictionary.
We show that the latter approach leads to the highest-resolution energy distribution and tracking performance.
1 INTRODUCTION
The wafer scanner mechatronic motion system is an
opto-mechanical machine for producing Integrated
Circuits (ICs) on a silicon wafer using a photolitho-
graphic process. One of the main components of a
wafer scanner is the six degrees of freedom (DOF’s)
wafer stage (Rotariu et al., 2003a). This is an electro-
mechanical servo system that positions the wafer
(200-300mm diameter) with respect to the imag-
ing optics. The wafer stage largely determines the
throughput (80-100 wafers/h, 80-200 ICs/wafer) and
the accuracy of the products, and they are both sub-
ject to severe performance requirements. Normal scan
speeds and accelerations are 0.5 m/s and 10 m/s
2
, re-
spectively. In order to maximize the throughput and
minimize the servo error of such a complex dynamical
system, advanced intelligent identification and con-
trol schemes are preferred to standard linear or robust
non-linear techniques (Casalino and Bartolini, 1984).
One of such advanced intelligent control schemes,
Iterative Learning Control (ILC), is an effective tech-
nique to reduce systematic control errors that occur in
systems that repetitively perform the same motion or
operation (Moore, 1993).
Although the time-domain ILC results can be ex-
tended to time-varying and nonlinear systems (Goh,
1994), the time-domain analysis does not give use-
ful frequency domain insights for the learning design.
In addition, the time-domain analysis results do not
address the issue of good transients and long-term
stability, and while different schemes for tuning of
the learning gain (Chang et al., 1992) have been pro-
posed, in (Wirkander and Longman, 1999) it has been
pointed out that the learning gain is not a critical fac-
tor to bandwidth. On the other hand, many frequency
domain analysis ILC algorithms have been proposed
based on frequency response methods and iteration
varying filter schemes (Tang et al., 2000), (Norrl
¨
of,
2002), but these do not give insightful time-domain
information for the learning design or they depend
heavily on the system model.
A logical advance of the above-mentioned time-
based and frequency-based ILC methods is to use
an ILC based on time-frequency analysis of control
signals. This has been first proposed in (Chen and
24
Rotariu I. and Vullings E. (2006).
DESIGN OF AN ITERATIVE LEARNING CONTROL FOR A SERVO SYTEM USING MULTI-DICTIONARY MATCHING PURSUIT.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 24-31
DOI: 10.5220/0001206400240031
Copyright
c
SciTePress
Moore, 2001), where an adaptive scheme of learning
feedforward control based on a B-spline network is
presented. In (Zhang et al., 2005) the use of wavelet
packet transform for time-frequency analysis and de-
sign of a cutoff frequency tuning for the ILC scheme
is proposed. In (Zheng and Alleyne, 2001), (Ro-
tariu et al., 2003a) continuous Wigner transform is
used to analyze the signals and in (Tharayil and Al-
leyne, 2004) and (Rotariu et al., 2006) an adaptive
robustness filter based on quadratic time-frequency
analysis (Wigner distribution) of the control signals
is proposed. In case of the Wigner distribution, exten-
sive studies have been made and methods (Cappellini
and Constantinides, 1984), (Rotariu et al., 2006) de-
vised to remove the cross-terms in some way, but
these methods do not improve the frequency resolu-
tion. Therefore, we have to focus on alternative meth-
ods that do increase the frequency resolution and re-
duce the cross-terms as well.
In this paper we propose an adaptive ILC based on
high-resolution time-frequency analysis of the con-
trol signals which is performed by means of signal
decomposition over a simple versus a complex time-
frequency atomic dictionary. We shall show that our
analysis in these two cases leads to a better under-
standing of the systems dynamics and more insightful
learning information than (piecewise) Wigner-based
adaptive ILC, while achieving a very good tracking
performance.
In Section II, the results of the signal analysis by
means of Wigner distribution will be used to find a
suitable profile for the bandwidth of the time-varying
robustness filter. In the end of this section it will be-
come clear that by increasing the resolution and accu-
racy of the time-frequency distribution, the tracking
performance of the ILC improves. In order to achieve
this, in Section 2.2 we shall introduce another two dif-
ferent time-frequency analysis methods of the servo
error signal than Wigner distribution; as consequence,
in Section 2.2 we shall show that the design of the
adaptive ILC changes and that this leads to very good
tracking performance of the proposed learning algo-
rithm.
2 TIME-FREQUENCY ADAPTIVE
ILC
This section discusses the time-frequency adaptive
ILC, i.e. time-varying adaptive ILC whose design is
based on quadratic time-frequency representation of
the control signals. Intuitively, this means that the
ILC ’gain’ is governed by the dynamics still present
in the error signal after the previous iteration: high
dynamic behavior leads to a large gain, low dynamic
behavior (noise) is ignored.
2.1 Time-varying Adaptive ILC
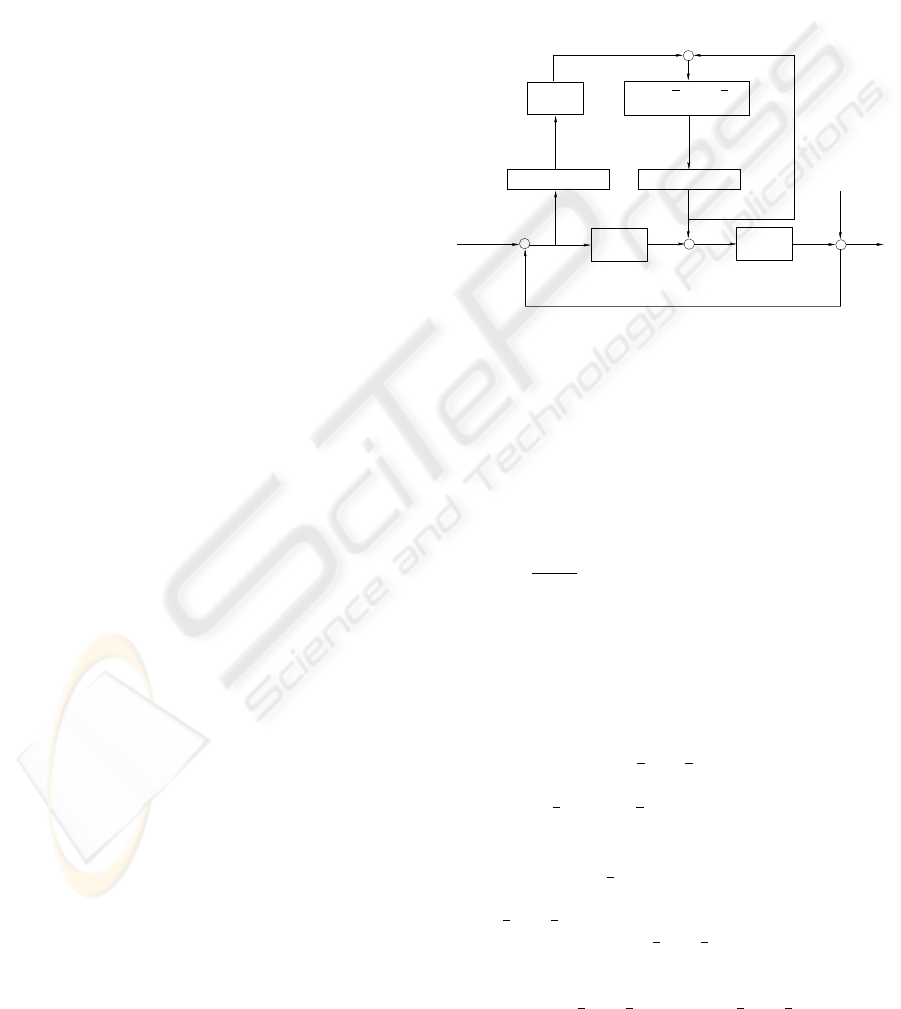
In this section the concept of time-varying adaptive
ILC is introduced (see Figure 1). We restrict the study
to the case where the plant is a causal, LTI dynamical
system P . C is a feedback controller which insures
the stability of the closed loop system.
We suppose that the desired response r is defined on
the interval (t
0
, t
f
), where t
f
≤ ∞ and the initial
conditions are the same at the beginning of each iter-
ation.
−
+
+
+
+
+
r
C
e
k
y
k
u
k
u
k+1
L
P
n
k
Q(·,
t, Ω
k
(t))
error table
FF table
Figure 1: A block schematic for adaptive ILC.
The goal of the ILC design is to find the feed-
forward signal u
∗
such that r = P u
∗
. We seek
a sequence of inputs u
k
with the property that
lim
k→∞
u
k
= u
∗
, where the index k is the iteration.
The adaptive ILC design consists of the design of
the L and Q filters. The learning filter L is the same
as for standard ILC, i.e. it has to approximate a sta-
ble inverse of the modeled process sensitivity function
P
s
(s) =
P
1+P C
(Rotariu et al., 2004).
The process sensitivity function as steady-state
transfer function is measured at the center wafer po-
sition and it does not account for system’s position
dependent dynamics within the scanning trajectory
(Rotariu et al., 2004) (Rotariu et al., 2003a) (Ro-
tariu et al., 2003b). We replace the fixed Q robust-
ness filter (steady-state filter, not changing from one
iteration to the other) of standard ILC with a time-
varying Q-filter Q
k
(s,
t, Ω
k
(t)), namely a zero-phase
low-pass Butterworth filter of order n and cut-off fre-
quency Ω
k
(t), where t ∈ [t
0(k)
, t
0(k)
+ T ], t
0(k)
is
the initial time of the k
th
iteration, and T is the time
required to perform the trajectory. The cut-off fre-
quency Ω
k
= Ω
k
(
t) may vary throughout the length
of each iteration. In what follows, we denote by
Γ
k
(t, t, Ω
k
(t)) the inverse Fourier transform of the
Butterworth filter Q
k
(s,
t, Ω
k
(t)) as a function in the
variable s:
Q
k
(s, t, Ω
k
(t))
F
−1
−→ Γ
k
(t, t, Ω
k
(t)). (1)
DESIGN OF AN ITERATIVE LEARNING CONTROL FOR A SERVO SYTEM USING MULTI-DICTIONARY
MATCHING PURSUIT
25

A converging (Rotariu et al., 2006) adaptive ILC
update law is given by
e
k
= e
r
− P
s
u
k
− Sn
k
, (2)
u
k+1
(t) =
Z
∞
−∞
Γ
k
(τ,
t, σ
k
(t))(u
k
+ Le
k
)(t −τ )dτ,
(3)
where e
k
is the error signal, u
k
the feedforward signal
and n
k
an output disturbance (see Figure 1). The for-
mula (3) is known as the nonstationary convolutional
integral (Margrave, 1998) which is an extension of the
convolutional method to nonstationary processes. We
refer to (Zheng and Alleyne, 2003), (Tharayil and Al-
leyne, 2004) and (Rotariu et al., 2006) for a rigorous
convergence analysis of our approach.
Next we present the design of the time-varying Q-
filter that is based on the time-frequency analysis of
the error signal.
2.2 Time-frequency Analysis of the
Servo Error Signal
We will present three alternative approaches to deter-
mine the time-frequency analysis of the servo error:
using Wigner, and matching pursuit with a single and
multiple dictionaries. Intuitively, the better the time-
frequency representation, the better will we be able to
reduce the servo error signal, and we therefore strive
for the best TF representation.
2.2.1 Wigner Distribution
The Wigner distribution (Mecklenbr
¨
auker et al.,
1997) is defined by
W
h
(t, f ) =
1
2π
∞
−∞
h
∗
t −
τ
2
h t +
τ
2
e
−2πjf τ
dτ,
(4)
where time t ∈ R in [s], the frequency f ∈ R in
[Hz], and h
∗
is the complex conjugate of the ana-
lyzed time-signal h. The distribution for real signals
is real-valued and can – due to its quadratic form – be
physically interpreted as the distribution of the sig-
nal’s energy over both time and frequency. Although
the Wigner distribution is especially appropriate for
the analysis of non-stationary multi-component sig-
nals (Cohen, 1989), its main deficiency is the cross-
term interference: each pair of signal components or
signal component and noise creates one additional
cross-term in the spectrum, thus the resulting time-
frequency representation may be confusing (see Fig-
ure 2).
Next we show how to eliminate the cross-terms
while maintaining a high-resolution energy distribu-
tion of the servo error.
e
r
− P
s
u
k
− Sn
k
,(2)
(3)
Figure 2: The absolute value of the Wigner distribution of
the servo error signal. Darker means higher relative en-
ergy. Seven intervals can be identified with significant en-
ergy content, of which three spurious ones (2, 4, and 6) due
to cross-terms. Note that also the non-spurious third and
fifth peaks are distorted by cross-terms.
2.2.2 Atomic Decomposition of the Servo Error
and Matching Pursuit in L
2
(R)
Decomposition of signals over window Fourier trans-
forms and wavelet transforms are the best known ex-
amples of signal decomposition over a family of func-
tions that are well localized in time and frequency. In
this section, we shall discuss time-frequency atomic
decomposition, also known as adaptive decomposi-
tion, of a signal and we shall describe a general it-
erative decomposition algorithm known as matching
pursuit (MP) (Mallat and Zhang, 1993). We shall also
explain why this atomic decomposition is well fitted
for servo error signal decomposition. Based on this
decomposition we shall show the servo error energy
distribution over a simple and complex atomic dictio-
nary.
MP is based on a family D of time-frequency atoms
that can be generated by scaling, translating and mod-
ulating a single window function g ∈ L
2
(R). We
suppose that the function g is real, continuously dif-
ferentiable, non-zero, g(0) 6= 0 and g(t) ∼ O(
1
1+t
2
).
In addition, we impose that kgk = 1 and that
R
R
g(t)dt 6= 0. For any scale s > 0, frequency mod-
ulation φ [Hz] and translation u, one defines
g
γ
(t) =
1
√
s
g(
t − u
s
)e
2π jφt
, (5)
with γ = (s, u, φ) ∈ R
+
× R
2
. The factor
1
√
s
nor-
malizes to 1 the L
2
norm of g
γ
. We also observe
that atoms defined in (5) look like φ-modulated ver-
sions of a doubly-indexed family of wavelets ψ
s,u
=
1
√
s
ψ(
t−u
s
), with the difference that for atoms one im-
poses the condition
R
R
g(t)dt 6= 0 while the admis-
sibility condition for wavelets requires
R
R
ψ(t)dt =
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
26

0. If g is even as in most situations, then g
γ
(t) is
well concentrated in time and frequency (Mallat and
Zhang, 1993).
The family D = {g
γ
}
γ
is extremely redundant
(Torresani, 1991). To represent any function h effi-
ciently, we must select an appropriate countable sub-
set of atoms {g
γ
n
}
n
so that
h =
∞
X
n=−∞
a
n
g
γ
n
. (6)
Consequently, for signals that include scaling and
highly oscillatory structures one cannot define a priori
appropriate constraints in scale and modulation para-
meters of the atoms g
γ
n
used in expansion (6). The
elements of the dictionary D = {g
γ
n
}
n
need to be
selected adaptively, depending on local properties of
the function h.
In our case, the servo error contains non-stationary
random structures (machine vibrations and sensor
noise), deterministic chaotic vibrations, and subhar-
monic oscillations that are known to demonstrate nar-
row high frequency support (Yen and Lin, 2000).
For this reason, the decomposition of error signals
over triple-indexed time-frequency atoms (5) enables
the extraction of signal features that combine non-
stationary, deterministic chaotic and transient chaotic
characteristics
Next we’ll give an outline of the MP algorithm
in the Hilbert space L
2
(R). We first approximate
h ∈ L
2
(R) with linear projections on elements of
D. Then it follows that
h =< h, g
γ
0
> g
γ
0
+ Rh, (7)
where Rh ∈ L
2
(R) is the residual after approximat-
ing h in the direction g
γ
0
. Since g
γ
0
is orthogonal on
Rh, it follows that
khk
2
= | < h, g
γ
0
> |
2
+ kRhk
2
.
To minimize kRhk, we chose g
γ
0
∈ D such that
| < h, g
γ
0
> | is maximum. After the first step
decomposition (7), we continue iteratively by sub-
decomposing the residual Rh by projecting it on a
vector of D that matches Rh the best, as we have done
for h. Therefore, we inductively obtain the m
th
order
decomposition of h over the dictionary D,
h =
m−1
X
n=0
< R
n
h, g
γ
n
> g
γ
n
+ R
m
h, (8)
where we denote by R
m
h the residual obtained at the
m
th
order decomposition of h. Using (8), one can
easily obtain the following important result:
Theorem.(Mallat and Zhang, 1993) If D is com-
plete (
span(D) = L
2
(R)) then
h =
∞
X
n=0
< R
n
h, g
γ
n
> g
γ
n
(9)
and
khk =
∞
X
n=0
| < R
n
h, g
γ
n
> |
2
. (10)
Remark. Finite linear expansions of time-
frequency atoms (5) are dense in L
2
(R) and therefore
this dictionary is complete.
The smallest complete dictionaries are bases. By
decomposing a signal onto an orthonormal bases of
compactly supported wavelets having a certain num-
ber of vanishing moments (Daubechies, 1991), cor-
relation between scales is avoided. One-dimensional
well localized in time (compactly supported) wavelets
are of the greatest interest for applications because of
the simplest numerical realization of expansion and
synthesis algorithms. The number of the vanishing
moments is especially important when one wants to
quickly compress large data sets. By using com-
pactly supported wavelets that have a relatively high
number of vanishing moments, the L
2
norm of the
residual will decrease faster than when using other
wavelets that have less vanishing moments. On the
other hand, for feature extraction tasks, choosing a too
high number of vanishing moments is not desirable as
we are interested in the non-redundant high frequency
components of the signal (Chandroth, 1999). In
other words, we are interested to decompose the sig-
nal into time-frequency atoms that describe the non-
smooth (nonlinear and nonstationary) behavior well
while preserving regular components of the servo er-
ror (Struzik and Siebes, 1998).
Next we show in Figure 3 the servo error decom-
position with respect to a simple atomic dictionary D
which is built with Symmlets. By applying the MP
algorithm, we found that the decomposition of the
analyzed servo error signal with respect to Symm-
lets with 9 vanishing moments provide the best re-
sults: for a given number of iterations, the L
2
norm
of the residuals given by formula (8) becomes smaller
than when using other simple atomic dictionaries, like
those that are built with Symmlets {4, 5, 6, 7, 8, 10},
Daubechies, Coiflets, and Haar wavelets.
At the end of this section we consider a com-
plex atomic dictionary D built with the asymmet-
ric Daubechies’ wavelets and by their more symmet-
ric and larger supported closely related cousins, i.e.
Symmlets and Coiflets (Daubechies, 1991). We ap-
ply the MP algorithm for the servo error decomposi-
tion with respect to this dictionary and we obtain a
smaller L
2
norm of the residuals (8) than when the
servo error is decomposed with Symmlets, see Fig-
ure 3. Through our numerical experiments we use a
quadrature mirror filter bank MP algorithm, see (Mal-
lat and Zhang, 1993), (Buckheit et al., 1995), (Rioul
and Vetterli, 1991).
Based on the decomposition (9) of any h ∈ L
2
(R)
over a simple or complex dictionary, and the defini-
DESIGN OF AN ITERATIVE LEARNING CONTROL FOR A SERVO SYTEM USING MULTI-DICTIONARY
MATCHING PURSUIT
27

0 2 4 6 8 10 12 14 16 18
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.2
x 10
4
Iteration
L
2
norm of the residuals
− stars represent decomposition with respect to different members of
the symmlet family 4,5,6,7,8,10 ;
− squares are obtained using symmlets 9 (best of the symmlet family);
− circles are obtained using our dictionary approach
Figure 3: The L
2
norm of the residuals (8) using a simple
atomic dictionary built with Symmlets. After a relatively
small number of iterations, Symmlets 9 show the best sig-
nal decomposition. The best results, however, are obtained
using our multi-dictionary approach.
tion of the Wigner distribution in (4), we obtain
W
h
(t, f ) =
∞
n=0
| < R
n
h, g
γ
n
> |
2
W
g
γ
n
(t, f )+
∞
n=0
∞
m=0,6=n
| < R
n
h, g
γ
n
> |
| < R
m
h, g
γ
m
> |W
n,m
,
where
W
n,m
=
1
2π
Z
R
g
γ
n
(t +
τ
2
)
g
γ
m
(t −
τ
2
)e
−2π jfτ
dτ
denotes the cross Wigner distribution of the atoms g
γ
n
and g
γ
m
.
The double sum corresponds to the cross-terms of
the Wigner distribution that we try to remove in or-
der to obtain a clear time-frequency distribution of
the signal h. We only keep the first sum and define
the energy distribution of the signal h over the time-
frequency plane as
E
h
(t, f ) =
∞
X
n=0
| < R
n
h, g
γ
n
> |
2
W
g
γ
n
(t, f ). (11)
By taking the absolute value of the energy distri-
bution defined in formula (11) with f = e
0
, when
the dictionary D = {g
γ
n
} is built with a complex
atomic dictionary generated by Symmlets, Coiflets
and Daubechies, we obtain the time-frequency energy
distribution plotted in Figure 4.
2.3 Design of a Bandwidth Profile
Next we shall design a bandwidth profile for the
time-varying robustness filter introduced in (1).
Figure 4: Servo error energy distribution using a multi-
dictionary wavelet packet generated by combining the
Daubechies, Symmlets and Coiflets atoms (selected MP
atoms are listed). The small insert zooms in to show the
’banana’ shapes, i.e. they consist of narrow-band subhar-
monic oscillations and chaotic vibrations.
Consider the time vector
t = (t
i
)
i∈N
; the initial
feedforward signal u
0
is chosen identically zero and
the error signal e
0
is the measured servo error when
a rigid body acceleration feed-forward is applied.
The elements of the vector Ω
0
(t) are chosen equally
small values, i.e. the initial time-varying robustness
filter is a steady-state filter whose bandwidth is
high enough (about 500 [Hz]) such that it does not
filter the deterministic content of the servo error.
Because of this choice and because the learning filter
L ∼ P
−1
s
behaves as a 1000 [Hz] low-pass filter,
by (2) it follows that the energy distribution of error
signal e
0
and feedforward signal u
1
are similar in
shape and for the design of the bandwidth Ω
1
(
t) it is
not important whether we analyze the servo error e
0
or its high bandwidth low-pass filtered version u
1
(
t).
The adaptive update law Ω
k
(t) → Ω
k+1
(t) for the
design of the time-varying bandwidth Ω
k
(
t) of the ro-
bustness filter Q
k
(s,
t, Ω
k
(t)) for any iteration k con-
tains the frequency envelope F
max,k
(
t) as gain. This
encompasses the frequencies of all signal components
at each time-instant whose energy exceeds C
e
, the
value of the noise during standstill:
F
max,k
(
t) = max(ω
k
(t)), for H
u
k
(t, ω
k
(t)) ≥ C
e
,
(12)
where H
u
k
is the time-frequency energy distribu-
tion of the feedforward signal u
k
, ω
k
(
t) is the cross-
section of H
u
k
and C
e
height plane (see Figure 5).
The envelope F
max
(t) is used as a gain in an adap-
tive update law. This law changes the bandwidth pro-
file Ω(t) after each iteration, when the effects of the
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
28

previous change on the measured error are evaluated.
After a new bandwidth profile has been implemented,
its benefit is evaluated by the function ∆N
k
(t), which
compares the local ℓ
2
norm of the current error to that
of the error at the previous iteration, such that
∆N
k
(
t) = N
k
(t) − N
k−1
(t) (13)
where
N
k
(t
i
) =
i+T
w
/2
X
j=i−T
w
/2
e
2
k
(t
j
), (14)
T
w
> 0 gives the width of the window where the sig-
nals are locally compared.
After introducing the terms F
max,k
(
t) and
∆N
k
(
t), we are now ready now to give the band-
width update rule
Ω
k+1
(
t) = Ω
k
(t) + ∆Ω
k
(t),
∆Ω
k
(
t) = F
max,k
(t) · ∆N
k
(t) · K
k
(t)
(15)
where the term K
k
(
t) = −sign(∆Ω
k−1
(t)) is in-
troduced to add the following logic to the mech-
anism: if the bandwidth was previously increased
(∆Ω
k−1
(t
i
) > 0), while the error decreased
(∆N
k
(t
i
) < 0), this change was beneficial and the
bandwidth may be further increased. On the other
hand, if an increase in the bandwidth resulted in a
larger error, this was obviously not the case and the
bandwidth should be lowered again. The combina-
tion ∆N
k
(
t) · K
k
(t) results in this kind of update
behavior.
Figure 5: A 3D-plot of the Wigner distribution for k = 1
(therefore of u
1
). The horizontal plane at energy value C
e
discriminates deterministic signal components from noise.
As the learning filter L ∼ P
−1
s
behaves as a 1000 [Hz]
low-pass filter, by (2) and (3) it follows that the energy dis-
tribution of error signal e
0
and feedforward signal u
1
are
similar in shape.
Applying the above algorithm in this section
with H
u
k
(
t, ω
k
(t))
def
≡ E
u
k
(t, ω
k
(t)) to the multi-
dictionary approach, we obtain he bandwidth profile
plot in Figure 6.
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
0
50
100
150
200
250
300
350
400
450
500
Time [s]
Ω[Hz]
The bandwidth Ω
The smoothed approximation of Ω
Figure 6: The bandwidth profile Ω(t) at iteration k = 1;
design based on the servo error energy distribution over the
complex time-frequency atomic dictionary found in the end
of Section 2.2.
Finally, in Figure 7 we show the servo error signal
when Adaptive ILC with the bandwidth of the Q-filter
as shown in Figure 6 is implemented on the wafer
stage test rig.
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
−4
−3
−2
−1
0
1
2
3
4
x 10
−7
Time [s]
Servo error [m]
using acceleration FF
using ILC, 3
rd
iteration
Figure 7: Error signal when rigid body accleration feedfor-
ward is applied and Adaptive ILC with the bandwidth of the
Q-filter as shown in Figure 6.
3 CONCLUSIONS
When comparing the resulting time-frequency energy
distributions in Figures 2 and 4, we note the follow-
ing:
DESIGN OF AN ITERATIVE LEARNING CONTROL FOR A SERVO SYTEM USING MULTI-DICTIONARY
MATCHING PURSUIT
29

The energy distribution based on the complex
atomic dictionary in Figure 4 is better localized in
time and frequency than the other. Also its resolu-
tion is much higher, and its high-energy deterministic
components can be much better separated from low-
energy stochastic components.
As we have announced, we are not only interested
in separating deterministic and stochastic components
in control signals, but also in separating their con-
stituents, i.e. periodic, subharmonic, chaotic and tran-
sient for deterministic nonlinear time-varying com-
ponents versus non-stationary and stationary for sto-
chastic components. The non-stationary and deter-
ministic chaotic vibrations present in the servo error
signal have narrow high-frequency support and are
difficult to be detected using Wigner distribution. By
applying the adaptive decomposition algorithm de-
scribed in Section 2.2.2, we are also able to identify
such narrow-band frequency characteristics, as can be
seen from the ‘banana’ shape of the dark patterns in
Figure 4, which are much more expressive than the
black patterns in Figure 2.
In Figure 2 the local cross-terms around t =
{0, 0.1, 0.2, 0.3} are not eliminated, while in Figure
4 they are not present anymore.
The energy plot in Figure 4 does not contain cross-
terms and any numerically undesired effects, as in
Figure 2.
Additionally, our multi-dictionary approach leads
to a clearer identification of time-varying non-linear
and stochastic servo error components and therefore,
to an improved adaptive ILC design.
We further observe that an overall smaller band-
width than in Figure 2 is obtained (not higher than
about 400 [Hz] in the beginning of the acceleration
profile and 100 [Hz] around other jerk moments).
Therefore, the ILC needs to learn only around these
jerk moments up to smaller frequencies than those
found when Wigner distribution was applied for the
computation of the bandwidth profile.
This means that the stochastic effects will not be
amplified unnecessarily (high bandwidth means good
tracking performance and noise amplification) while
all existent deterministic effects will be learned. Also,
unlike in Figure 2, we do not obtain any increased
bandwidth because of cross terms: the bandwidth of
the Q-filter needs to be increased just around the jerk
moments while, in between, a small bandwidth can be
maintained.
Also, as seen in Figure 4, the bandwidth profile has
a very good smooth approximation. Therefore, fast
switching between the cut-off frequency of Q-filters
that corresponds to different time instances is avoided
and the stability of the switched ILC system is not an
issue anymore.
REFERENCES
Buckheit, J., Chen, S., Donoho, D., Johnstone, I., and Scar-
gle, J. (1995). Wavelab. In Tech. Rep., Stanford Uni-
versity.
Cappellini, V. and Constantinides, A. (1984). Interference
terms in the Wigner distribution. Digital Signal Proc.
Casalino, G. and Bartolini, G. (1984). A learning proce-
dure for the control of movements of robotic manipu-
lators. In Proc. 4th IASTED Symp. Robotics Automa-
tion, pages 108–111.
Chandroth, G. O. (1999). Diagnostic classifier ensembles:
Enforcing diversity for reliability in the combination.
In University of Sheffield, UK.
Chang, C.-K., Longman, R. W., and Phan, M. Q. (1992).
Techniques for improving transients in learning con-
trol systems. Adv. Astronautic. Sci, 76:20352052.
Chen, Y. and Moore, K. (2001). Frequency domain adap-
tive learning feedforward control. In Proc. of the 2001
IEEE Int. Symp. Comp. Intell. Robotics and Automa-
tion, pages 396–401.
Cohen, L. (1989). Time-frequency distributions – a review.
Proc. IEEE, 77(7).
Daubechies, I. (1991). Ten lectures on wavelets. Series in
Applied mathematics, SIAM.
Goh, C. J. (1994). A frequency domain analysis of learn-
ing control. J. Dynamic Syst., Measurement, Contr.,
116:781–786.
Mallat, S. and Zhang, Z. (1993). Matching pursuit with
time-frequency dictionaries. IEEE Trans. on Signal
Processing, 41(12):3397–3415.
Margrave, G. F. (1998). Theory of nonstationary linear fil-
tering in the fourier domain with applications to time-
variant filtering. Geophysics, 63(1):244 – 259.
Mecklenbr
¨
auker, W., Hlawatsch, F., and Janssen, A. (1997).
The wigner distribution, theory and applications in
signal processing. Elsevier.
Moore, K. L. (1993). Iterative learning control for de-
terministic systems. Adv. in Ind. Control. Springer-
Verlag.
Norrl
¨
of, M. (2002). Iteration varying filters in iterative
learning control. In Proc. 4th Asian Control Conf.,
page 21242129.
Rioul, O. and Vetterli, M. (1991). Wavelets and sig-
nal processing. IEEE Signal Processing Magazine,
8(4):14–38.
Rotariu, I., Dijkstra, B., and Steinbuch, M. (2004). Com-
parison of standard and lifted ilc on a motion system.
In 3rd IFAC Symp. Mechatronic Systems, Sydney, Aus-
tralia, pages 211–6.
Rotariu, I., Ellenbroek, R., and Steinbuch, M. (2003a).
Time-frequency analysis of a motion system with
learning control. In Proc. ACC Conf., pages 3650 –
3654. American Control Conf.
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
30

Rotariu, I., Ellenbroek, R., and Steinbuch, M. (2006).
Adaptive iterative learning control with application to
a wafer stage. submitted to IEEE Transactions on
Control Systems Technology.
Rotariu, I., Ellenbroek, R., van Baars, G., and Steinbuch, M.
(2003b). Scan-length independent iterative learning
control applied to a wafer stage motion system. In
Proc. ECC Conf.
Struzik, Z. and Siebes, A. (1998). Wavelet transform in sim-
ilarity paradigm i and ii. In Centrum voor Wiskunde
en Informatica, Report,INS-R9802.
Tang, X., Cai, L., and Huang, W. (2000). A learning
controller for robot manipulators using fourier series.
IEEE Trans. Robot. Automat., 16(1):3645.
Tharayil, M. and Alleyne, A. (2004). Design and conver-
gence of a time-varying iterative learning control law.
In Proc. IMECE Int. Mech. Eng. Congr. and R&D
Expo.
Torresani, B. (1991). Wavelets associated with represen-
tations of the afine weyl-heisenberg group. J. Math
Physics, 32(5):1273–9.
Wirkander, S.-L. and Longman, R. (1999). Limit cycles for
improved performance in self-tuning learning control.
Adv. Astronautic. Sci., 102:763–781.
Yen, G. and Lin, K. (2000). Wavelet packet feature ex-
traction for vibration monitoring. IEEE Trans. Ind.
Electronics, 47(3):650–67.
Zhang, B., Wang, D., and Ye, Y. (2005). Wavelet transform-
based frequency tuning ilc. IEEE Trans. Systems, Man
& Cybernetics, Part B: Cybernetics, 35(1):107–114.
Zheng, D. and Alleyne, A. (2001). Adaptive iterative
learning control for systems with non-smooth non-
linearities. In Proc. ASME Conf., Pittsburgh, Penn-
sylvania. ASME Int. DETC.
Zheng, D. and Alleyne, A. (2003). Stability of a novel iter-
ative learning control scheme with adaptive filtering.
In Proc. ACC Conf.
DESIGN OF AN ITERATIVE LEARNING CONTROL FOR A SERVO SYTEM USING MULTI-DICTIONARY
MATCHING PURSUIT
31
