DIFFERENT CLASSIFIERS FOR THE PROBLEM OF

EVALUATING CORK QUALITY IN AN INDUSTRIAL SYSTEM

Beatriz Paniagua-Paniagua, Miguel A. Vega-Rodríguez, Juan A. Gómez-Pulido,

Juan M. Sánchez-Pérez

Dept. Informática, Univ. Extremadura, Escuela Politécnica, Campus Universitario s/n, 10071, Cáceres, Spain

Keywords: Image processing, industrial application, cork quality, automated visual inspection system, classifiers.

Abstract: In this paper we study the use of different classifiers to solve a classification problem existing in the cork

industry: the cork stopper/disk classification according to their quality using a visual inspection system.

Cork is a natural and heterogeneous material, therefore, its automatic classification (usually, seven different

quality classes exist) is very difficult. The classifiers, which we present in this paper, work with several

quality discriminators (features), that we think could influence cork quality. These discriminators (features)

have been checked and evaluated before being used by the different classifiers that will be exposed here. In

this paper we attempt to evaluate the performance of a total of 4 different cork quality-based classifiers in

order to conclude which of them is the most appropriate for this industry, and therefore, obtains the best

cork classification results. In conclusion, our experiments show that the Euclidean classifier is the one

which obtains the best results in this application field.

1 INTRODUCTION

The most important industrial application of cork is

the production of stoppers and disks for sealing

champagnes, wines and liquors. In fact, according to

the experts, cork is the most effective product,

natural or artificial, for the sealed (Fortes, 1993). In

the cork industry, stoppers and disks are classified in

different quality classes based on a complex

combination of their defects and particular features.

Due to this, the classification process has been

carried out, traditionally, by human experts

manually.

At the moment, there are several models of

electronic m

achines for the classification of cork

stoppers and disks in the market. The performance

of these machines is acceptable for high quality

stoppers/disks, but for intermediate or low quality,

the number of samples classified erroneously is

large. In conclusion, the stoppers/disks should be re-

evaluated by human experts later. This slows down

and increases in price the process enormously. Think

that, on average, a human expert needs a minimum

training period of 6 months to attain a minimum

agility, although the learning process lasts years

(compare it with other experts: wine tasters, cured

ham tasters, etcetera). Another negative aspect is the

subjectivity degree added to the classification

process due to the necessary human re-evaluation.

We have to add to these antecedents the fact that

ain is the 2

world producer of cork (CorkQC,

2006), only surpassed by Portugal, and that in

Extremadura (a south-western region of Spain), for

its geographical situation, the cork industry is one of

its more important industries: it produces 10% of the

world cork (ICMC, 2006).

All these motivations have lead us to the

evelopment of this research, whose main objective

is the construction of a computer vision system for

cork classification based on advanced methods of

image processing and feature extraction in order to

avoid the human evaluation in the quality

discrimination process.

For this purpose we have performed a study of

e features that could better inform us about the

cork quality. We have focused this study on an

analysis of thresholding techniques (segmenting the

different cork defects) and textural features, in

addition to other features (like holes and different-

area defects). From this study we conclude that the

features that better define the cork quality are: the

total cork area occupied by defects, the cork texture

104

Paniagua-Paniagua B., A. Vega-Rodr

ıguez M., A. G

omez-Pulido J. and M. S

anchez-P

erez J. (2006).

DIFFERENT CLASSIFIERS FOR THE PROBLEM OF EVALUATING CORK QUALITY IN AN INDUSTRIAL SYSTEM.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 104-111

 SciTePress

contrast, the cork texture entropy, and the biggest

size defect in the cork stopper/disk.

Later, and with these results, an analysis of

different possible classifiers has been made. The

studied classifiers have been a Back-Propagation

neural network, the K-means classification

algorithm, a K-nearest neighbours classifier and the

minimum Euclidean distances classification

algorithm. In this paper we evaluate all these

classification algorithms with the purpose of

knowing which of them is the most appropriate for

our application environment.

The rest of the paper is organized as follows:

section 2 describes briefly the tools and the data

used for the development of our experiments. In

section 3, we present the features used by the

classifiers. Then, section 4 shows the theoretical

bases for the analysis we have made and other

important details. Finally, section 5 presents the final

results statistical evaluation for each classifier, while

section 6 exposes the conclusions and future work.

2 TOOLS AND DATA

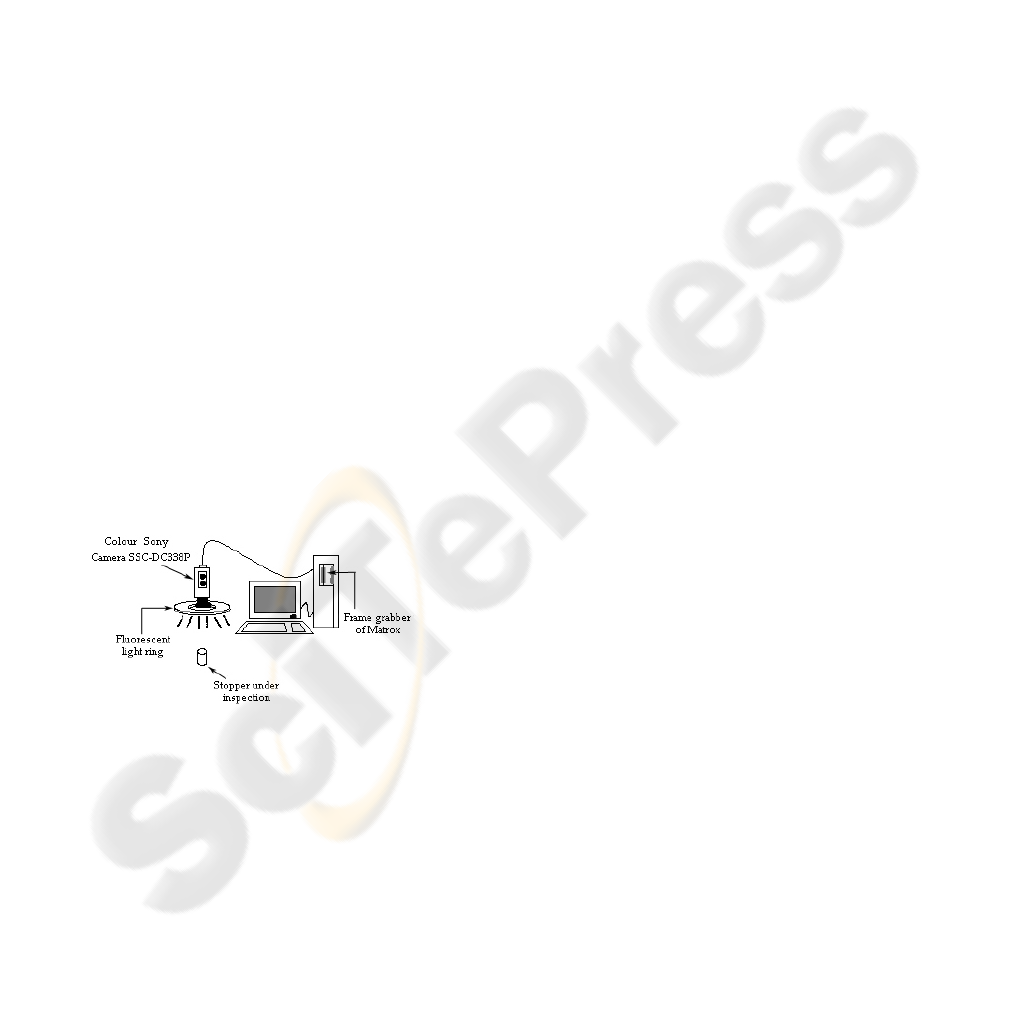
At present, the computer vision system we use to

acquire the cork stopper/disk images is formed by

the elements shown in figure 1: the host (a Pentium

processor), a colour Sony camera (SSC-DC338P

model), the illumination source (fluorescent-light

ring of high frequency -25 KHz- of StockerYale),

and a METEOR 2/4 frame-grabber of Matrox, with

the software required for the image acquisition

(MIL-Lite libraries of Matrox).

Figure 1: Computer vision system.

On the other hand, the database used in our

experiments consists in 700 images taken from 350

cork disks (we have taken two images of each disk,

for both heads). There are seven different quality

classes, 50 disks in each class. The initial

classification, in which this study is based on, has

been made by a human expert from ASECOR (in

Spanish: “Agrupación Sanvicenteña de Empresarios

del CORcho”, in English: “Cork Company Group

from San Vicente-Extremadura”). We suppose this

classification is optimal/perfect and we want to

know which classifier obtains the most similar

classification results.

3 USED FEATURES

In order to develop our classifiers study, different

feature extraction methods were analysed:

thresholding techniques, statistical texture analysis,

etcetera.

Regarding automatic thresholding, we carried

out a study of global and local thresholding

techniques (Sonka, 1998) (Sahoo, 1988). The

objective was to extract the defect area from the cork

area, thus being able to extract the percentage of the

cork area occupied by defects (an important feature

in cork quality discrimination). 11 global

thresholding methods were studied: static

thresholding, min-max method, maximum average

method, Otsu method, slope method, histogram

concavity analysis method, first Pun method, second

Pun method, Kapur-Sahoo-Wong method,

Johannsen-Bille method and moment-preserving

method. In general, global thresholding methods are

very limited in our problem. For a good global

thresholding we need bimodal histograms, and the

results obtained with unimodal histograms have

been quite bad. These methods are suitable for the

cork stopper/disk area extraction from the image

background. In this situation we can find that all

conditions for a good operation are fulfilled, but they

are not suitable for the defect area extraction from

the cork area. As for local thresholding, two

methods have been studied: statistical thresholding

method and Chow-Kaneko method. The local

thresholding methods have been more suitable than

the global methods for the solution of our problem.

This has been due to they are able to find better

thresholds in unimodal histograms. Nevertheless, the

increase of the computational cost can make them

unsuitable for our problem. Taking into account all

these considerations, the best of all these methods

applied to our problem was static thresholding

method with a heuristically fixed threshold in the

gray level 69.

With regard to texture analysis (Haralick, 1973)

(Shah, 2004), two main methods have been studied,

both based on statistical texture analysis. The first

was a method based on simple co-occurrence

matrices and another was a method based on

rotation-robust normalized co-occurrence matrices.

Furthermore, we have studied nine quality

discriminators (textural features) for each method:

energy, contrast, homogeneity, entropy, inverse

difference moment, correlation, cluster shade,

cluster prominence and maximum probability. The

DIFFERENT CLASSIFIERS FOR THE PROBLEM OF EVALUATING CORK QUALITY IN AN INDUSTRIAL

SYSTEM

105

best obtained results were with the contrast and the

entropy, both calculated by using rotation-robust

normalized co-occurrence matrices.

In addition to the total area occupied by defects

(obtained after doing an image thresholding with the

previous methods) and the texture analysis of the

cork area, other features were analysed too.

Concretely, additional studies were made on: holes

(perforations) in the cork area and size of the

biggest defect in the cork. In the case of cork holes, a

quantitative comparison is done between the

theoretical area of cork (computed using the cork

stopper/disk perimeter) and the real area of cork. If

the real area is smaller than the theoretical one

(surpassing certain threshold) we consider that the

cork has holes. In order to calculate the biggest

defect in the cork stopper/disk, the followed

methodology is to perform successive morphological

erosions on the thresholded image (defects area). In

each iteration, we control the remaining defect

percentage. In this way, we can quickly observe the

size that could have the biggest defect of the cork,

analysing the number of required iterations for

eliminating almost all the defect pixels (or required

iterations for reaching certain threshold of defect

pixels). The best results obtained in this case (the

evaluation of these two additional features) were for

the size of the biggest defect in the cork.

In conclusion, after an exhaustive feature study,

the features chosen to be used in our classifier study

were: the total cork area occupied by defects

(thresholding with heuristic fixed value 69), the

textural contrast, the textural entropy and the size of

the biggest defect in the cork.

4 METHODS

In this paper, in order to classify a cork disk in a

specific class, we will use the corresponding

classification algorithm base on the four features

selected: defects area, contrast, entropy, biggest

defect size. The four classifiers chosen for this study

are the following (Shapiro, 2001) (Sonka, 1998): a

Back-Propagation neural network, a K-means

classifier, the K-nearest neighbours classification

algorithm, and a minimum Euclidean distance

classifier.

4.1 Neural Classifier

Concretely, we have developed a Back-Propagation

neural network. An artificial neural network

represents a learning and automatic processing

paradigm inspired in the form in which the nervous

system of the animals works. It consists in a

simulation of the properties observed in the

biological neural systems through mathematical

models developed with artificial mechanisms (like a

computer). In the case of this problem, a Back-

Propagation network architecture has been chosen,

very suitable for pattern recognition and class

detection. The network designed for this study has

the following architecture:

• One input layer that is the one that receives

external signals, which will be the four features

selected during the course of this work.

Therefore, the input layer has 4 neurons.

• One hidden layer, whose number of neurons is

based on the proportion given by the following

equation:

Therefore, and knowing that the output layer

has 3 neurons, the number of hidden neurons

should be 6. But, at the end, we decided to

increase the number of neurons in the hidden

layer and increase the complexity of the weight

matrix. In this way, we make easier the learning

for the network. Due to this fact, our hidden

layer has 7 neurons.

• One output layer that gives back the results

obtained by the neural network in binary format.

As the classes to classify are seven, only 3

neurons will be necessary to codify the results

correctly.

The weights associated to the network

interconnections are initialized randomly and are

adjusted during the learning. The type of learning

used by this neural network is supervised. That is,

we present to the network pairs of patterns (an

entrance and its corresponding wished exit). While

we are showing patterns to the network, the weights

are adjusted so that the error between the real results

and the desired ones is diminished. This process is

repeated until the network is stable. After this phase,

we can run the neural network.

4.2 K-Means Classifier

As always, we have studied this classifier for the

four selected features. We have decided to study the

reliability of this classifier because of its consecrated

fame in specialized literature. This classification

algorithm makes reference to the existence of a

number of K classes or patterns, and therefore, it is

necessary to know the number of classes. We know,

a priori, that we have 7 classes, reason why the

algorithm is suitable for our necessities. K-means

ICINCO 2006 - ROBOTICS AND AUTOMATION

106

classification algorithm is a simple algorithm, but

very efficient, and due to this fact it has been so

used.

Beginning from a set of p objects to classify X

, …, X

, the K-means classification algorithm

makes the following steps:

Step 1

Knowing previously the number of classes, we

say K, K samples are randomly chosen and clustered

into arrays (see the following equation), and these

arrays will be the centroids (due to the fact of being

the only elements) for each class.

Step 2

Being this algorithm a recursive process with a

counter n, we can say that in the generic iteration n

we allocate all the samples {X}

1≤j≤p

among the K-

classes, as we can observe in the following equation:

In the previous equation we have indexed the

classes (that are dynamic classes) and their

centroids.

Step 3

In the moment we have allocated all the samples

among the different classes, it is necessary to update

the class centroids. With this calculation, we are

looking for to minimize the profit index that is

shown in the following equation:

This index can be minimized using the sample

average of α

(n) (see the following equation):

Being N

(n) the number of samples in class α

after the iteration n.

Step 4

We check if the classification algorithm has

reached the stability, as it is shown in the following

equation:

If it does, the algorithm finishes. If not, we

return to step 2 for repeating all the process again.

Finally, we have to say that, for the centroids

allocation, the distance shown in the following

equation was used. This is the Euclidean distance

scaled with the standard deviation instead of with

the variance, which gave better results in a previous

study.

4.3 K-Nearest Neighbours Classifier

As for the classification algorithm based on the K-

nearest neighbours, we can say that also works with

the four best features obtained in the study about

cork quality, above-mentioned. The distance

selected for this experimentation was the Euclidean

distance scaled with the standard deviation (showed

before). We have decided this according to the

results obtained for the Euclidean classifier.

This algorithm is part of the methods group

known as correlations analysis methods. It consists

in classifying an unknown feature vector, depending

on the sample or K samples of the training set that

is/are more similar to it, or what is the same, which

is/are nearer to this vector in terms of minimum

distance. The used distance more suitable for this

method is the Euclidean distance. This is what we

know as rule of the nearest neighbours. The

classification algorithm of the K-nearest neighbours

even can be very efficient when the classes have

overlapping, and this is very interesting for our

problem (cork quality classes).

A first brute-force approach for this algorithm

computes the distance between the unknown feature

vector and all the samples in the database (training

set), it stores all these distances, and then it classifies

the unknown vector in the class whose samples gave

more minimum distances (in this case, many

distances have to be examined). One of the

advantages of this approach is that new samples can

be added to the database at any time, but it also has a

higher calculation time.

A better approach is to examine only the K

nearest neighbours (samples) to the unknown vector,

and to classify it based on those K-neighbours. The

class of the unknown feature vector will be the one

that have most of the K-neighbours. This has been

the approach implemented in our classification

algorithm.

4.4 Euclidean Classifier

This classifier is one of the simplest and most

efficient classifiers. This classifier has also been

used to observe the tendency (goodness) of all the

features previously studied, analysing which of all

the studied features were more suitable for cork

quality discrimination.

The classification algorithm supposes several

classes with their respective prototypes (centroids).

Given an unknown feature vector to classify, the

Euclidean classifier will associate this vector to the

DIFFERENT CLASSIFIERS FOR THE PROBLEM OF EVALUATING CORK QUALITY IN AN INDUSTRIAL

SYSTEM

107

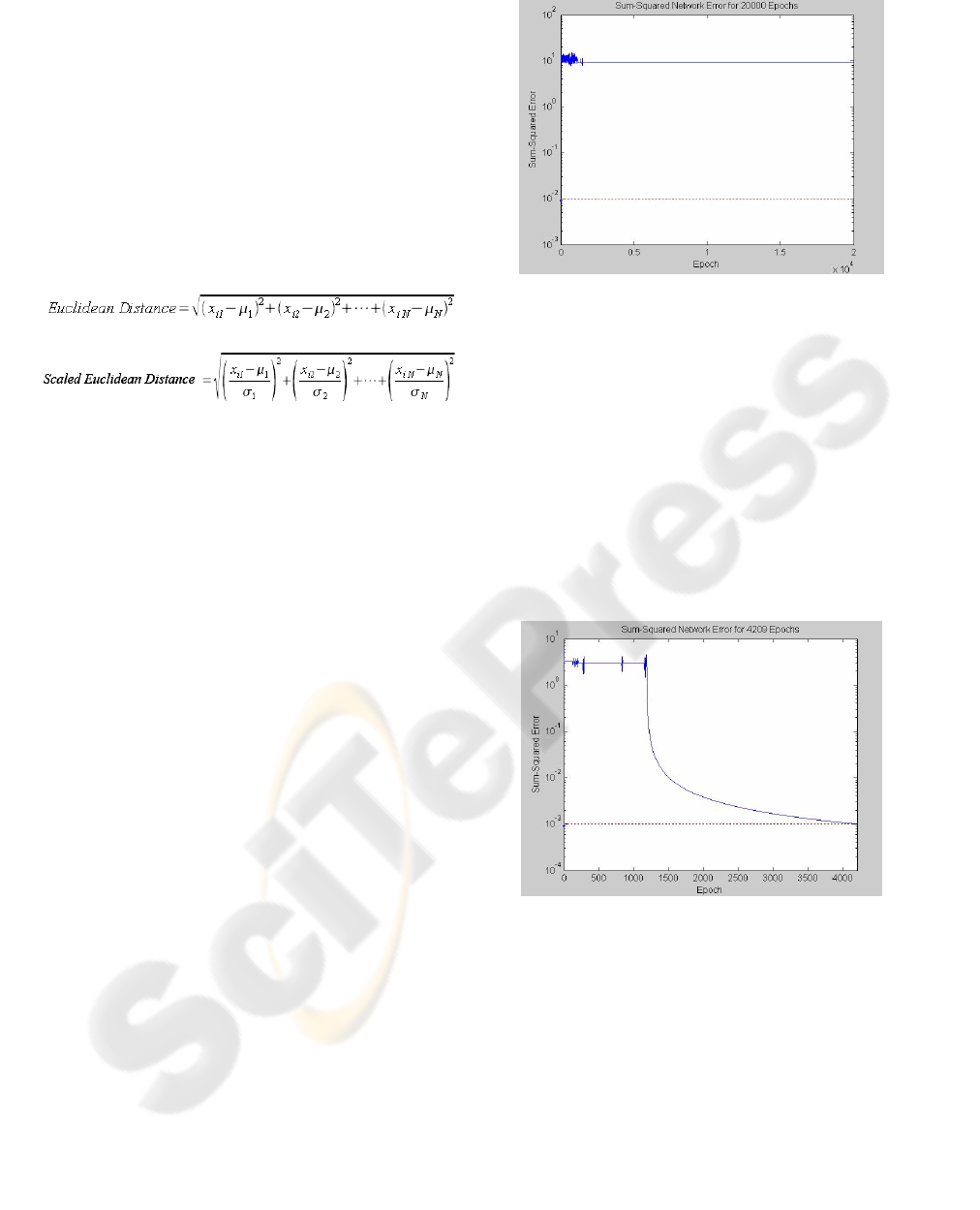
class whose prototype is closest to it, that is, the

prototype whose Euclidean distance is smallest.

Our study have been made for four versions of

the Euclidean distance: simple Euclidean distance

(see equation below), Euclidean distance with

prefiltrate (certain corks were classified directly,

without passing the Euclidean classifier, to low-

quality classes if a hole in them was detected, that is,

we used a set of decision rules in addition to the

Euclidean classifier), scaled Euclidean distance (see

equation below) and modified scaled Euclidean

distance, according to the standard deviation (see

equation in section 4.2).

The best results were obtained by the two last

distances, but the modified scaled Euclidean

distance was chosen for being more balanced in the

results.

5 RESULTS

The results of this section have been obtained using

the 4 classification algorithms previously explained.

We present these results by means of confusion

matrices (Shapiro, 2001), due to their capability to

show the conflicts among the different quality

categories. Therefore, not only the definition of each

class will be displayed, but also the main confusions

among them.

5.1 Neural Classifier

The experimental results that are shown in this

section correspond to a simplified version of the

neural network. This decision was taken due to the

non convergence of the network, when it was tried

to learn the seven cork quality classes. Although we

normalized the input data in a range from 0 to 24,

and made a preselection of the cork disks that were

more adapted to be training patterns, the

convergence was impossible.

Figure 2: Graph showing the non convergence.

As it can be observed in figure 2, with the first

version of the neural network, it was impossible to

reach the convergence of the network, and the error

introduced in the classification was too high. The

dotted line shows the level of ideal error established

(0.01), and the solid line shows the real error in the

classification (around 10 points). The shown result

was obtained after 20000 iterations of the network.

After multiple tests with the neural network, it

was verified that, probably due to the overlapping

between contiguous classes, the network was only

able to learn two classes, for example, class 0 and

class 3.

Figure 3: Graph showing the convergence of the network.

As it is shown in figure 3, with this second

version (and even after having lowered the

maximum level of error to 0.001), the neural

network reaches the convergence quickly, in only

4209 iterations.

After this explanation, we can present the results

of the confusion matrix. Table 1 shows the

confusion matrix for the neural classifier. As it was

expected, we have obtained quite bad results due to

the class overlapping. Since the neural network only

recognizes two classes, all the corks are classified in

class 0 or class 3. Anyway, the results are coherent,

ICINCO 2006 - ROBOTICS AND AUTOMATION

108

it can be observed as classes 0 and 3 are classified

mainly in themselves. Classes 4, 5 and 6, which are

more distant from class 0, are classified mainly in

class 3. And classes 1 and 2 are those that present

more confusion between class 0 and 3 for being

between them.

Table 1: Confusion matrix for the neural classifier.

C0 C1 C2 C3 C4 C5 C6

C0 36 0 0 14 0 0 0

C1 28 0 0 22 0 0 0

C2 15 0 0 35 0 0 0

C3 12 0 0 38 0 0 0

C4 8 0 0 42 0 0 0

C5 3 0 0 47 0 0 0

C6 2 0 0 48 0 0 0

In conclusion, table 2 presents the final results,

with a wrong classification percentage of 78.85%.

Table 2: Total results for the neural classifier.

C0 C1 C2 C3 C4 C5 C6 TOT.

Wrong 14 50 50 12 50 50 50 276

Right 36 0 0 38 0 0 0 74

5.2 K-Means Classifier

Table 3 displays the confusion matrix for the K-

means classifier.

Table 3: Confusion matrix for the K-means classifier.

C0 C1 C2 C3 C4 C5 C6

C0 39 0 8 3 0 0 0

C1 25 0 15 9 0 0 1

C2 5 0 20 23 0 1 1

C3 1 0 7 24 4 3 11

C4 0 0 3 9 12 19 7

C5 0 0 0 7 17 24 2

C6 0 0 1 6 17 22 4

The confusion matrix we have obtained offers

good results, although we can observe that there is a

class that almost disappears, class 1. Nevertheless,

the other classes have many right classifications,

except class 6. In this sense, a great absorption

power of class 5 over classes 4 and 6 is observed.

The matrix presents only a little dispersion, which is

very positive for the classification.

In conclusion, the final wrong classification

percentage is 64.85% (table 4).

Table 4: Total results for the K-means classifier.

C0 C1 C2 C3 C4 C5 C6 TOT.

Wrong 11 50 30 26 38 26 46 227

Right 39 0 20 24 12 24 4 123

5.3 K-Nearest Neighbours Classifier

For the calculation of the best size of K, three

possible values have been checked. The chosen

values were the following:

- A little value, K=10.

- A big value, K=49, the number of cork

disks in a class (50) minus the disk under

study.

- A medium value, K=20.

After a preliminary test, we finally concluded

that the best size of K is K=20. Once we have

chosen the value of K, we have done our

experiments using the Euclidean distance that has

generated the best results, the scaled Euclidean

distance according to the standard deviation (see

equation in section 4.2).

Table 5 presents the confusion matrix for the K-

nearest neighbours classifier. As we can observe in

the matrix, we have obtained good results. The

matrix has a strong classification tendency around

the main diagonal for all the classes, although it

would be possible to say that still there are many

erroneous classifications in some classes.

Table 5: Confusion matrix for the K-nearest neighbours

classifier.

C0 C1 C2 C3 C4 C5 C6

C0 38 9 3 0 0 0 0

C1 24 15 11 0 0 0 0

C2 8 12 20 9 1 0 0

C3 1 8 10 16 10 2 3

C4 1 0 4 13 15 7 10

C5 0 0 2 7 12 10 19

C6 0 0 4 4 11 16 15

In conclusion, the final error rate (table 6) is

63.14%.

Table 6: Total results for K-nearest neighbours classifier.

C0 C1 C2 C3 C4 C5 C6 TOT.

Wrong 12 35 30 34 35 40 35 221

Right 38 15 20 16 15 10 15 129

DIFFERENT CLASSIFIERS FOR THE PROBLEM OF EVALUATING CORK QUALITY IN AN INDUSTRIAL

SYSTEM

109

5.4 Euclidean Classifier

The obtained confusion matrix (table 7) presents

quite positive results. Using a classifier based on

scaled Euclidean distances with the standard

deviation, we can observe that class 6 acquires a

great power of absorption, that even affects class 4.

On the other hand, we can see a strong

discrimination of classes 0, 6 and 3, with a great

number of corks classified rightly in these classes.

Table 7: Confusion matrix for the Euclidean classifier.

C0 C1 C2 C3 C4 C5 C6

C0 33 12 4 1 0 0 0

C1 19 14 13 3 1 0 0

C2 6 9 15 18 2 0 0

C3 1 4 7 23 11 0 4

C4 2 0 1 10 13 3 21

C5 0 0 1 12 7 6 24

C6 1 0 1 7 7 3 31

The total results are shown in table 8, with a

final wrong classification percentage of 61.42%.

Table 8: Total results for the Euclidean classifier.

C0 C1 C2 C3 C4 C5 C6 TOT.

Wrong 17 36 35 27 37 44 19 215

Right 33 14 15 23 13 6 31 135

6 CONCLUSIONS AND FUTURE

WORK

The automatic visual inspection of cork is a problem

of great complexity, in what refers to its quality-

based classification, because cork is a natural

material, and therefore, highly heterogeneous. This

heterogeneity causes that cork quality depends on

many combined factors, and among them, cork

texture, defect area, size of the biggest defect,...

In this paper we have performed a deep survey

about several classifiers that includes each of these

features (the best features we have found in a

previous research). Concretely, we have focused on

four important classifiers in the image processing

field.

According to the experimental results we can say

that, in case of cork, there are more suitable

classifiers than others, although some of the studied

classifiers have been very near in their final results.

As final conclusion, we can say that the Euclidean

classifier has been the more reliable in our

application field. Figure 4 presents the wrong

classification percentage obtained by the different

classifiers. This graph also includes the wrong

classification percentage that a random classification

would have obtained if it was used.

Figure 4: Final results for the studied classifiers.

As we can observe in the previous graph, the

Euclidean classifier has produced the best results,

but it is worthy to say that all the studied

classification algorithms improve the results

obtained by a random classification, although the

goodness of the obtained results widely varies

between some classifiers and others.

Furthermore, we think the results and

conclusions obtained in this study can be useful to

other visual inspection researches focused on other

natural materials (wood, slate, etcetera), because

they have common characteristics with the cork

(heterogeneity, defects, changing texture according

to their quality,...).

As future work we have planned to study other

classifiers like, for example, fuzzy-neural networks.

Also, we do not discard the inclusion and analysis of

other features that could improve the classification

results.

ACKNOWLEDGEMENTS

This work has been supported in part by the Spanish

Government under Grant TIN2005-08818-C04-03.

REFERENCES

CorkQC, The Natural Cork Quality Council, 2006.

Industry Statistics. At

http://www.corkqc.com.

Fortes, M.A., 1993. Cork and Corks. In European Rev.,

vol. 1, pp 189-195.

Haralick, R.M., Shanmugam, K., Dinstein, I., 1973.

Textural Features for Image Classification. In IEEE

Transactions on Man and Cybernetics, vol. 3, pp 610-

621.

ICINCO 2006 - ROBOTICS AND AUTOMATION

110

ICMC, Instituto del Corcho, Madera y Carbón Vegetal,

2006. Instituto de Promoción del Corcho (ICMC-

IPROCOR). At http://www.iprocor.org, Spain.

Sahoo, P.K., Soltani, S., Wong, A.K.C., 1988. A Survey of

Thresholding Techniques. In Computer Vision,

Graphics, and Image Processing, vol. 41, pp 233-260.

Shah, S.K., Gandhi, V., 2004. Image Classification Based

on Textural Features Using Artificial Neural Network

(ANN). In IE(I) Journal-ET, vol. 84, pp 72-77.

Shapiro, L.G., Stockman, G.C., 2001. Computer Vision,

Ed. Prentice Hall, New Jersey.

Sonka, M., Hlavac, V., Boyle, R., 1998. Image

Processing, Analysis and Machine Vision, Ed. PWS

Publishing, USA, 2

edition.

DIFFERENT CLASSIFIERS FOR THE PROBLEM OF EVALUATING CORK QUALITY IN AN INDUSTRIAL

SYSTEM

111