HYBRID IMPEDANCE CONTROL FOR MULTI-SEGMENTED

INSPECTION ROBOT Kairo-II

C. Birkenhofer, S. Studer, J. M. Z

ollner, R. Dillmann

Forschungszentrum Informatik (FZI)

Haid-und-Neu-Str. 10-14, 76131 Karlsruhe, Germany

Keywords:

Hybrid Impedance Control, Multi-Segmented Robot, Force Feedback, Dynamic Modeling.

Abstract:

The tremendous redundancy of the multi-segmented robot Kairo-II can be utilized to enhance general robot

conﬁguration by any inspection task. To do so, an extensive control scheme must be installed which can handle

both, contact scenarios with the environment and ambiguous robot conﬁgurations. A method for implementing

an appropriate scheme using Transposed Jacobians based on Hybrid Impedance Control (TJ-HIC) is described

and validated for multi-segmented robots. Crucial parts of this model are identiﬁed and implemented. These

are dynamic modeling of the robot in Recursive Newton-Euler equations (RNE) and a sensory system for

apropriate force feedback information.

1 INTRODUCTION

Hyper-redundant systems offer great opportunity and

present great challenges for control tasks. Trajec-

tory planning, hybrid position and force control and

handling redundancy require extensive control tech-

niques. The multi-segmented robot Kairo-II is a

hyper-redundant system. Its expanse, load capacity

and kinematic abilities make it appropriate for inspec-

tion operations in unstructured environments.

We term the end-effector of the robot ”conﬁgurable”

as different segments of the robot fulﬁl characteristics

of the end-effector. According to serial kinematics

both head- and tail-segment of Kairo-II (Figure 1) can

be interpreted as end-effector of an open kinematic

chain, depending on the driving direction, with head

and tail segments as the robot base, respectively. The

redundancy of the system furthermore can be used

to position inspection segments within the kinematic

chain. In this case head and tail segment represent the

base of the robot. This process can be deﬁned as an

additional user-deﬁned task. The kinematic chain of

the system gets closed and gives rise to a major con-

straint for any control strategy arises.

Such movement offers greater opportunity for inspec-

tion tasks, but calls for complex control strategies.

Deadlocks have to be detected and resolved in a ap-

propriate way. Fundamental methods for manipulator

control can be used.

The paper is organized as follows. First, the con-

Figure 1: Multi-segmented inspection robot MAKRO-

plus (similar in construction to Kairo-II). A typical robot

conﬁguration consists of 6 drive segments and 5 joint seg-

ments.

trol architecture of the Kairo-II robot is presented in

section 2. Crucial blocks of the control loop are here

identiﬁed. Section 3 presents fundamentals of the dy-

namic model of the robot. This model is essential for

simulating the control loop. The sensory system for

217

Birkenhofer C., Studer S., M. Zöllner J. and Dillmann R. (2006).

HYBRID IMPEDANCE CONTROL FOR MULTI-SEGMENTED INSPECTION ROBOT Kairo-II.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 217-222

DOI: 10.5220/0001207602170222

 SciTePress

force detection is presented in section 4. Finally, sys-

tem integration and experimental results are analyzed

in detail in section 5. Summary and future work are

addressed in section 6.

2 CONTROL ARCHITECTURE

2.1 Transpose Jacobian based

Hybrid Impedance Control

In performing inspection tasks, a robot usually inter-

acts with the surrounding environment. Position con-

trolled methods can not fulﬁl demands of such an op-

eration. In fact simultaneous control of position and

force is necessary. Numerous basic strategies exist

(Salisbury, 1980), (Hogan, 1985) and (Khatib, 1987).

In the ﬁeld of redundant systems those strategies have

to be enhanced for two reasons:

• Ambiguity of coordinate transformations have to

be handled.

• Decomposition of redundancy is usually managed

by velocity controlled systems. Such systems tend

to proper motion.

For these reasons, Hybrid Impedance Control, based

on Transposed Jacobian (Shah and Patel, 2005) was

chosen in the presented work. Main advantages of the

control scheme are:

• The control algorithm is deﬁned in the working

space of the system.

• Accurate knowledge of the robot’s dynamic is not

necessary.

• Any higher instance for controlling the system can

be integrated.

In terms of controlling a user-deﬁned task as de-

scribed in section 1 the essential requirements are ful-

ﬁlled. Structure and crucial components of the con-

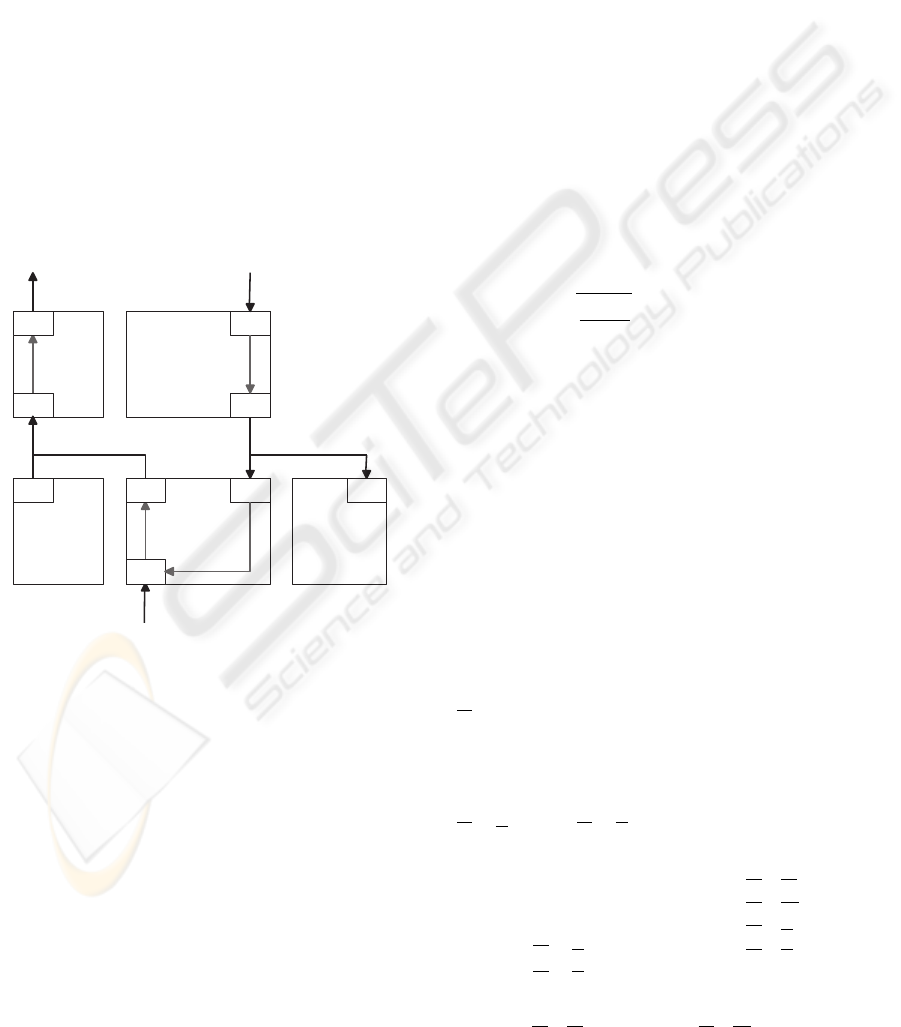
trol scheme are depicted in Figure 2. The control loop

consists of an inner and an outer loop. While the outer

loop generates desired cartesian acceleration trajec-

tories, the inner loop controls needed motor torques

directly. Redundancy of the system and possible sub-

tasks are both handled in the inner loop.

Several blocks of the control loop have decisive char-

acter in hybrid force and motion control of the multi-

segmented robot Kairo-II. Their impact on the control

scheme is presented below.

2.2 Trajectory Generation

Generation of the robot’s trajectory is equivalent to

a transformation of a low-dimensional vector to a

HIC

Trajectory

Generation

Integrator

Potential

Function

Forward

Kinematics

Robot

G(q)

Jacobian

Outer Loop

Inner Loop

[ ]

Figure 2: Transpose Jacobian based Hybrid Impedance

Control, (X

: Vector of the desired trajectory, X

: Vec-

tor of the reference position trajectory, Z

: Vector of the

desired sub-task, Y

: Vector of desired task requirements,

: contact force with the environment).

higher one. In taking redundancy into account a sim-

ple (low-dimensional) primary task shall be gener-

ated.

Kairo-II posesses tremendous kinematic abilities.

Since this is a hyper-redundant system, tasks can be

enhanced by addition of aspects (i.e. placing a sen-

sory module) in the process of the trajectory genera-

tion. Generation of the robot’s path will be processed

according to the virtual line / curve algorithm (Scholl

et al., 2000). This master-slave method is simple, ro-

bust and efﬁcient. By using this method the high-

dimensional input vector gets reduced to a lower di-

mensoinal one, as only the head-segment has to be

taken into account when generating a trajectory. In

contrast to other methods (i. e. (Choset and Henning,

1999)), the mechanical constraints of the robot are

taken into account in the trajectory generation phase.

The generated trajectory is therefor driveable for the

robot.

When the environment the robot is driving becomes

increasingly complex and unstructured, an adapta-

tion towards the virtual tube algorithm (Birkenhofer

et al., 2005) is desirable. Trajectory generation will

then work in a higher-dimensional space. Not only

the head-segment but segments essential for the addi-

tional sub-tasks are taken into account.At this stage,

trajectory generation will be kept at a basic level to

demonstrate the control loop’s working principle.

2.3 Potential Function

As part of the inner control loop, the potential func-

tion acts as a quality factor for desired movements.

Aspects of optimization are taken into account to deal

with the redundancy of the system. There are several

criterea possible.

• Gravity keeps the components of the robot on the

ground

• Minimize absolute value of all joint amplitudes

• Move inspection module to a desired position,

adapt and keep the robot in a steady state.

ICINCO 2006 - ROBOTICS AND AUTOMATION

218

Currently, a criterion that minimizes movements of

all joints is adequate. Steady state considerations will

follow.

2.4 Dynamic Modeling

The quality of dynamic modeling of Kairo-II has a

large impact on the system’s performance (in contrast

to general TJ-HIC-applications) for two reasons:

First, good simulation of the robot is important in the

early design phase of Kairo-II. (I.e. The model’s ac-

curacy has an impact on evaluating force feedback

sensor system.)

Second, the use of the robot within a closed loop re-

quires knowledge of the robot’s dynamics for inverse

dynamic and kinematics calculations. (I.e. Posture

control of the robot has to be evaluated with regard

to the robot’s steady state when a user-deﬁned addi-

tional task is processed.) The module for dynamic

modelling is integrated in the work ﬂow as depicted

in Figure 3.

Data

Fusion

Force Feedback

section 4

Inverse Dynamics

(RNE-model)

section 3

Robot

Kairo-II

Direct

Dynamics

sense

model

f, n

q, q’, q’’

Figure 3: Work ﬂow of the dynamic modeling and the force

feedback sensor system as implemented in MCA2.3 (Scholl

et al., 2001).

2.5 Force Feedback

When Kairo-II is in motion, we receive sensor val-

ues stating the current forces and moments within the

robot. This is a result of the motion of the robot and its

contact with the environment. At the same time, the

dynamic model calculates forces and moments result-

ing from the sheer robot motion not considering con-

tact with the environment. In merging sensor values

with model values, we are able to calculate the exter-

nal forces that act on the robot, Therefore, we assume

adequate accuracy of the sensor system and the robot

model. A sensor system based on strain gauge tech-

nology is therefore integrated in the module ”Force

Feedback” (see Figure 3).

3 DYNAMIC MODELING

For the successful implementation of the proposed

control scheme it is of great importance to design an

appropriate dynamic model of Kairo-II. There exist

various approaches to describe the dynamics of rigid

multi-body systems. Most of them face two common

problems: It’s hard to deﬁne the parameters and the

computational complexity exceeds the capacity of a

mobile system.

A modeling method that is quite efﬁcient is the Recur-

sive Newton-Euler equation (RNE) (Fu et al., 1987).

In considering each robot link (rigid part between two

joints) separately, forces and moments that apply to it

can be calculated recursively. The two well-known

physical laws can be used. We apply them to rotating

coordinate systems:

d(m

)

= m

d(I

)

= I

˙ω

+ ω

× (I

)

(1)

with force F, mass m, velocity v, acceleration a, mo-

ment N, inertia I and angular velocity ω of the i-th

link.

The formulation results in two sets of recursive equa-

tions: The forward equations propagate kinematics

information such as angular velocity, angular accel-

eration and linear accelerations from the head of the

robot to the tail. The backward equations propagate

the forces and moments exerted on each link from the

tail to the head.

To make the algorithm computationally more efﬁ-

cient, all values are referenced to the local coor-

dinate system of the corresponding joints instead

of computing them to the coordinate system of the

head. This is demonstrated by multiplying the values

with the appropriate 3 × 3 rotating matrices, where

i−1,i

transforms any vector with reference to co-

ordinate system (x

, y

, z

) to the coordinate system

i−1

, y

i−1

, z

i−1

Inputs of the model are the current joint positions q

joint velocities ˙q

and joint accelerations ¨q

, while

n,0

n+1

and R

n,0

n+1

are the forces and moments

exerted by link n upon the environment.











˙q

¨q

n,0

n+1

n,0

n+1











RNE

=⇒











i,0











(2)

(With i = 1 . . . n). The model outputs the total exter-

nal force R

i,0

and moment R

i,0

exerted on link

HYBRID IMPEDANCE CONTROL FOR MULTI-SEGMENTED INSPECTION ROBOT Kairo-II

219

COM

i,0

i-3,0

i-3

i-3,0

i-3

i-3,0

i-3

i,0

i-3,0

i-3

link i

link i-3

j-1

i-4

i-1

i-3

i-4

i-5

i-1

i-2

Figure 4: Simpliﬁed dynamic model of Kairo-II.

i at the center of mass (COM) for the links i = 1 . . . n.

Furthermore it returns the forces R

i,0

and moments

i,0

exerted on link i by link i − 1 at the position

of joint i and the input force/torque τ

for joint i.

Each link is speciﬁed by a set of 14 parameters, which

describe the kinematics of the link, its mass and its in-

ertia. So, to describe the robot Kairo-II in its standard

conﬁguration with 6 segments and 15 joints, more

than 200 parameters would have to be deﬁned. Fur-

thermore, the values of inertia have to be determined

for each of them.

3.1 Simpliﬁed Dynamic Modeling

To avoid the problem of complexity, a simpliﬁed

model of the robot is presented. As two segments of

Kairo-II are linked by three joints, we would have to

deﬁne 3 · 14 = 42 parameters. We replace the three

real joints by three virtual joints (J

, J

i−1

, J

i−2

), that

are centred at one point just in between two segments

(see Figure 4). The joint’s coordinate systems have

the same origin, and their axes of rotation form an or-

thogonal coordinate system.

In this way the links i−1 and i−2 are zero-links with

mass, inertia and displacement vectors all being zero.

As a result the number of parameters to determine de-

creases from 42 to 20.

This also reduces the enormous number of output val-

ues of our model. With the reduced model all out-

put forces/moments are located either at the center of

mass of the segments or at the location of the virtual

joints which simpliﬁes the interpretation of the values

and the integration into the control scheme.

4 SENSOR SYSTEM

The TJ-HIC control scheme needs information about

forces and moments arising within the real robot. By

fusing this sensor information with data from the dy-

namic model, differential data can be obtained. F

model

− F

sense

. With F

as differential force af-

ter the robot’s contact with the environment. In mini-

mizing F

a movement close to the desired movement

generated by the trajectory planner is achieved.

In installing a sensor system for force feedback, major

effort has to be put into the sensor’s position. Accord-

ing to Figure 4 the sensor’s coordinate systems should

match to the dynamic modeling systems. Therefore, a

sensor system is presented that is able to detect forces

and moments in the model’s coordinate systems.

Three sensor applications fulﬁl these requirements.

They provide information on arising forces and mo-

ments along the axes of the dynamic model or can be

at least transformed easily.

Rotation around x-axis Implicit torque measure-

ment within rotational gears

Forces along y-, z-axis Explicit torque measurement

within mechanic components (ﬂange plate)

Forces along x-axis Explicit torque measurement by

analyzing drive segment motor currents

The biggest impact on constraint motion is provided

by explicit torque measurement along y- and z-axis.

As a result of this, sensory feedback virtual tube can

be adapted to minimize torsions that affect the ma-

nipulator. Gathering this sensory information is de-

scribed in the next sections. Measuring torques and

forces along the x-axis is not covered in this paper.

4.1 Architecture

For a typical robot conﬁguration of 6 drive segments

and 5 joint segments and well-known masses of the

components, a detection of arising torques of about

25 N m to 200 Nm is desirable to be detected. By

making this information available, adaptation of the

virtual tube is possible. The linear structure of the

robot, minding the law of the levers, prefers torques

to forces for analysis. Torques in direction of y- and

z-axes are to be measured. Any combination of those

vectors is valid.

Analyses in (Birkenhofer et al., 2004) have proven

that force and torque primarily affect the ﬂange plate.

Deformations resulting of affecting forces are here to

be measured best. The presented sensor system meets

requested accuracy. It is based on strain gauge tech-

nology.

To detect the direction of affecting moments non-

ambiguously, a sensor array is necessary. Three pairs

of sensors with an angular distance of 60 degree are

installed. Therefore, six pairs of strain gauges are ap-

plied. Opposing strain-gauges in each case make up a

full measuring bridge, providing optimal temperature

compensation. The positions of the single sensors are

named w

1+/−

, w

2+/−

, w

3+/−

. Thereby, three sensor

signals are derived: w

1..3

According to the general strain-gauges equation

∆R

∆U

= k.

∆l

(3)

ICINCO 2006 - ROBOTICS AND AUTOMATION

220

maximal sensor resolution (i.e. minimal detectable

elongation δl) can be achieved by optimizing three

sets of parameters:

• Enhancing circuits voltage U respectively resis-

tance R.

• Scaling down factor k, which is subject to material

properties.

• Minimizing SNR of the sensors circuitry.

While items 1 and 2 underlie mechanical constraints,

major work has been put into SNR reduction of the

electrical circuitry, sensor’s cabling and sensor’s ﬁx-

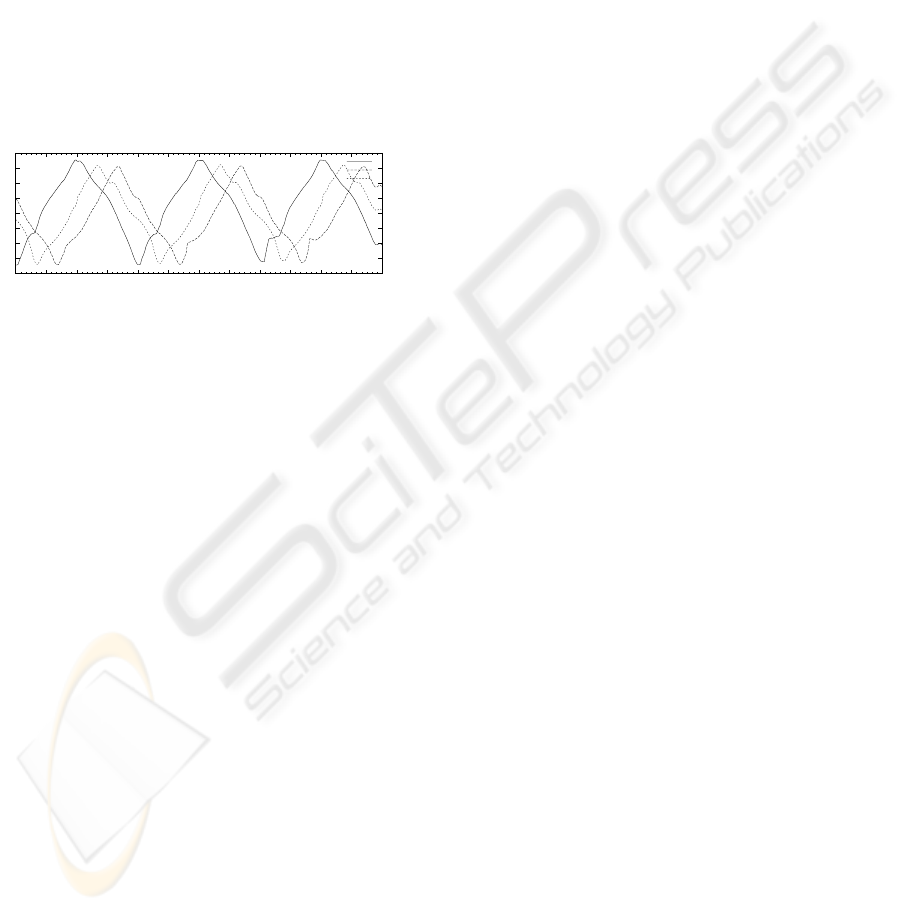
ing. As a result an ampliﬁcation factor of k = 5826

results in a signal’s amplitude of about 4000 LBS

(with noise in a range of 500 LSB).

-4000

-3000

-2000

-1000

1000

2000

3000

4000

0 90 180 270 360 450 540 630 720 810 900 990 1080

-4000

-3000

-2000

-1000

1000

2000

3000

4000

degrees

Strain Data (DS

;CYCLE

auto

)

Figure 5: A constant load that is rotating around the ﬂange

plate causes alternating amplitutes of sensor signals w

1..3

(x-axis: angle in deg, y-axis: sensor value in LSB).

As seen in Figure 5 angular detection of applying

forces are possible. The sensor meets the control

scheme’s demands.

4.2 Signal Optimization

Three primary factors affect sensory accuracy and

therefore reduce measurement reading interpretation

respectively:

Hysteresis Measured magnitude is at a maximum of

about ±1 µm/m strain

Long-term drift is in a range of about ±1.25 µm/m

strain

Temperature compensation’s residual error is

compensated by a linear approach. An auto-ﬁt

algorithm is used, to minimize the error signal q

(

(j) −

+ p

· T (j)

; ∀j

)

(4)

With j as a single tuple in the data series, w

(j)

as current strain value and T (j) as the according

temperature. The algorithm optimizes q

by min-

imizing the least square error e(p

, o

) iteratively.

The algorithm will be aborted after ﬁve iterations,

as the auto-ﬁtting process results then in a remain-

ing residual error in a range of ±50 counted mea-

surands for the falling branch of temperature. This

equals to ±0.25 µm/m, which is close to the de-

sired sensor resolution.

In order to apply torques to the ﬂange plate’s deforma-

tion, the direct sensor model maps three sensor signals

, w

] to moments [M

, M

] according to axes

y,z of the ﬂange plate coordinate system. A calibra-

tion will determine a set of model parameters C for

a provided set of calibration data, comprising l data

tuples [M

, M

, w

]

; 1 ≤ λ ≤ l.

Therefore, we need some approximation with coefﬁ-

cients c

∈ C:

≈ c

1,0

1,1

1,2

+..+c

1,7

.. (5)

≈ c

2,0

2,1

2,2

+..+c

2,7

.. (6)

As this is an over-determined, linear equation sys-

tem, least squares method provides optimal solution

by querying all calibration data tuples for either M

or M

. The vector of variables can be created in dif-

ferent ways. In this work, the expressions (7) and (8)

render best results.

lin

= [ 1 w

] (7)

poly

= [ 1 w

)

...

...(w

)

]

(8)

lin

is simple and stable, W

poly

is better suited to

cope with deformations or harmonics at the inﬂection

points of the strain signals. Vectors which include

cross product terms (as w

· w

) do not respond in

an adequate way.

5 INTEGRATION & RESULTS

In this paper the TJ-HIC control scheme was

presented and identiﬁed as adequate for an imple-

mentation in the multi-segmented inspection robot

Kairo-II. Two major function blocks of this scheme

were presented in detail: dynamic modeling and the

force feedback sensor. Outputs of both are to be

fused in a further function block to close the control

loop.

5.1 Sensor System

Some optimization criteria have been presented to

deal with the sensor’s accuracy. As a result we get an

angular and amplitude decomposition of the signal

which is presented in table 1. The presented results

indicate a good angular resolution (Birkenhofer et al.,

HYBRID IMPEDANCE CONTROL FOR MULTI-SEGMENTED INSPECTION ROBOT Kairo-II

221

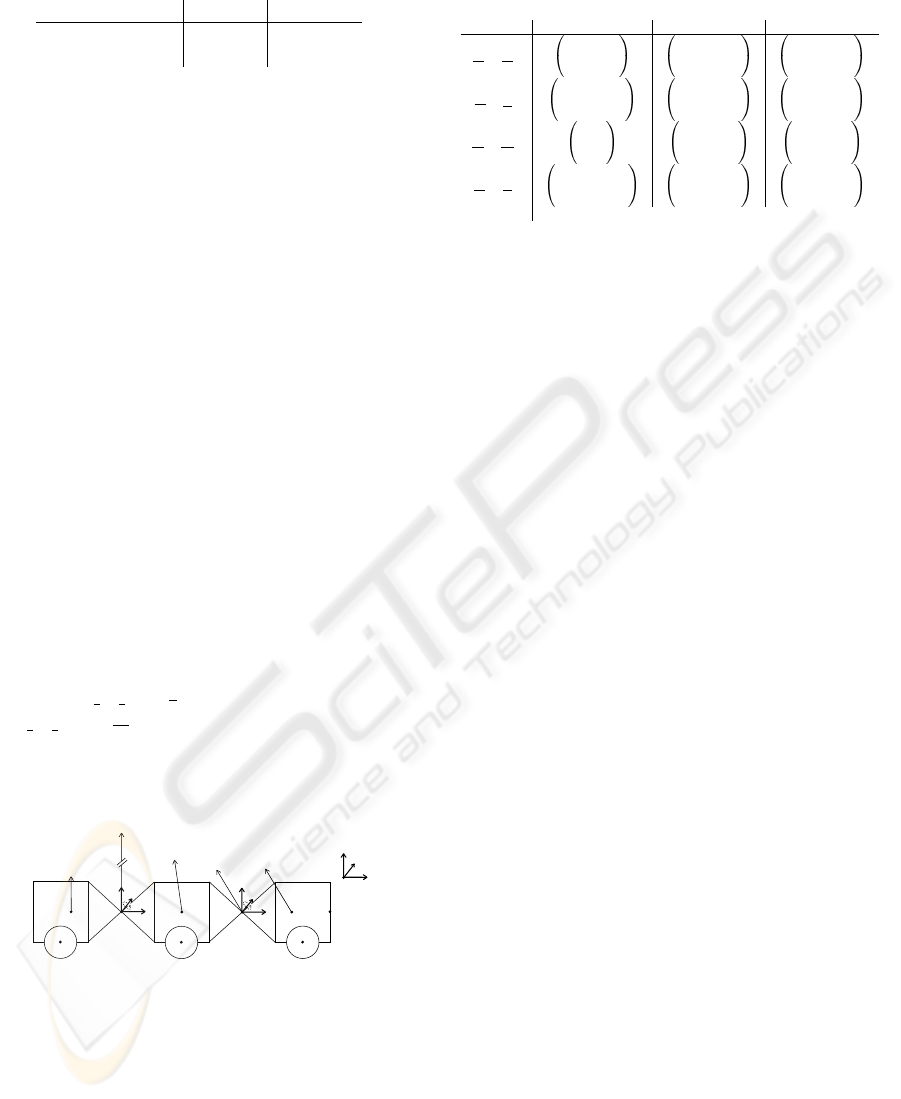
Table 1: Angular and amplitude decomposition.

25 Nm 200 Nm

angular error ±19

◦

±12, 8

◦

amplitude error ±26% ±18, 3%

2005). Amplitude resolution can be optimized by

complex material analyses. As we use the signal

for impedance control, the signal’s quality can be

weighted by impedance control factors M

, B

and

. A focus on the angular resolution signal is

therefore possible. With this method inﬂuence of the

amplitude of the signal can be minimized, whereas

the angular value of the signal gets strengthened.

5.2 Dynamic Modeling

The dynamic modeling of Kairo-II has been realized

as functional block in the software framework MCA.

Appropriate coordinate systems have been identiﬁed

to handle both efﬁcient calculations within the model

and simple sensor fusion with other modules. There-

fore, a simpliﬁed dynamic modeling was introduced

that meets the mechanical requirements and reduces

the number of parameters drastically.

Sensor fusion can be implemented in a new module

easily, as all data sources (dynamic modeling, sensor

system) provide data in similar coordinate systems.

The following example depicts the working prin-

ciple of the algorithm (see Figure 6). All robot

joints are positioned in their nullposition. The robot

is ﬁxed at its left end. In applying joint veloci-

ties (ALPHA M qd) 3

and joint accelerations (AL-

PHA M qdd) 3

to all joints. Forces and moments

within the system arise. They can be calculated ac-

cording to the RNE algorithm. Results are presented

in table 2 and depicted as vectors in Figure 6.

4,0

7,0

4,0

link 7

link 4

1,0

link 1

8,0

COM COM COM

Figure 6: Robot conﬁguration with three segments.

6 CONCLUSION

A control scheme for multi-segmented robots was

presented. As controlling the robot’s redundancy is

both challenging and promising, this scheme can han-

dle the ambiguity of the system. Crucial modules of

the TJ-HIC scheme were identiﬁed and implemented

in this paper. As the other - relevant - modules of the

Table 2: Sensor Outputs of the RNE algorithm (forces [N],

moments [Nm]).

i 1 4 7

i,0

67.17

−14.19

99.47

−50.06

82.85

i,0

−64.25

249.49

−64.25

182.31

−50.06

82.85

i,0

−0.41

−0.34

i,0

−106.28

−54.71

−10.29

control scheme (i.e. trajectory planning and potential

function) are kept to minimal complexity, the control

loop can be closed now.

Future work has to be done in the ﬁeld of not only

handling but using the redundancy of Kairo-II. In do-

ing so, huge driving capabilities are expected. The

system is then able not only to fulﬁll a main task but

also an user-deﬁned subtask like positioning an in-

spection module or avoiding obstacles.

REFERENCES

Birkenhofer, C., Hoffmeister, M., Z

ollner, J.-M., and Dill-

mann, R. (2005). Compliant motion of a multi-

segmented inspection robot. In IRS, Edmonton.

Birkenhofer, C., Scholl, K.-U., Z

ollner, J.-M., and Dill-

mann, R. (2004). A new modular concept for a multi-

joint, autonomous inspection robot. In (IAS 8).

Choset, H. and Henning, W. (1999). A follow-the-leader

approach to serpentine robot motion planning. SCE

Journal of Aerospace Engineering.

Fu, K., Gonzalez, R. C., and Lee, C. G. (1987). Robotics

- Control, Sensing, Viion and Intelligence. McGraw-

Hill International Editions.

Hogan, N. (1985). Impedance control: An approach to ma-

nipulation, parts i - iii. ASME J. Dynam. Syst., Meas.,

Contr., 107:1–24.

Khatib, O. (1987). A uniﬁed approach to motion and force

control of robot manip ulators: The operational space

formulation. IEEE Journal on Robotics and Automa-

tion, 3(1):43–53.

Salisbury, K. (1980). Acitve stiffness control of manipula-

tors in cartesian coordinates. IEEE Int. Conf. Robotics

and Automation, pages 95–100.

Scholl, K.-U., Albiez, J., and Gassmann, B. (2001). Mca -

an expandable modular controller architecture. In 3rd

Real-Time Linux Workshop.

Scholl, K.-U., Kepplin, V., Berns, K., and Dillmann, R.

(2000). Controlling a Multi-joint Robot for Au-

tonomous Sewer Inspection. In ICRA.

Shah, M. and Patel, R. (2005). Transpose jacobian based

hybrid impedance control of redundant manipulators.

In CCA, pages 1367– 1372.

ICINCO 2006 - ROBOTICS AND AUTOMATION

222