
A 16-BIT SWITCHED-CAPACITOR SIGMA-DELTA
MODULATOR MATLAB MODEL EXPLOITING TWO-STEP
QUANTIZATION PROCESS
Lukas Fujcik, Radimir Vrba
Faculty of Electrical Engineering and Communication, Brno University of Technology, Udolni 53, Brno, Czech Republic
Miroslav Sveda
Faculty of Information Technology, Brno University of Technology, Bozetechova 2, Brno, Czech Republic
Keywords: Sigma-delta modulator, switched-capacitor technology, quatization process.
Abstract: This paper presents a novel architecture of high-order single-stage sigma-delta (ΣΔ) converter for sensor
measurement. The two-step quantization technique was utilized to design a novel architecture of ΣΔ
modulator. The time steps are interleaved to achieve resolution improvement without decreasing of
conversion speed. This technique can be useful for low oversampling ratio. The novel architecture was
designed to obtain high dynamic range of input signal, high signal-to-noise ratio and high reliability. The
proposed architecture of switched-capacitor (SC) ΣΔ modulator was simulated with blocks containing
nonidealities, such as sampling jitter, noise, and operational amplifier parameters (white noise, finite dc
gain, finite bandwidth, slew rate and saturation voltages). The novel architecture of SC ΣΔ modulator with
two-step quantization process was designed and simulated in MATLAB SIMULINK.
1 INTRODUCTION
High-resolution analog-to-digital conversion based
on Σ∆ modulation has become commonplace in
many measurement applications including audio,
seismic, biomedical and harsh environment sensing.
Σ∆ methods incorporating oversampling and noise
shaping provide improved resolution over Nyquist-
rate conversion methods by trading component
accuracy for time. However, this AD converter
architecture requires both filtering and
downsampling of the oversampled signal, or
decimation filtering (Norsworthy et al., 1997).
The ΣΔ modulation relies on oversampling, which
means that all operations, like an integration AD and
DA conversion, have to be performed within
roughly the same time. If any operation takes
significantly longer time than others, it will limit the
speed, and consequently dynamic range. ΣΔ
modulators can be implemented either with
continuous-time or with sampled-data techniques.
The most popular approach is based on a sampled-
data solution with SC implementation. For this
reason, we will focus on the case of SC modulators
in this paper. In fact, SC modulators can be
efficiently realized in standard CMOS technology
and included in complete mixed-signal systems
without any performance degradation.
In the design of a high-performance SC
modulator, two main issues have to be addressed by
the designers.
1) Which is the best architecture to fulfill the
application requirements?
2) For a given architecture, which are the
requirements for the building blocks?
2 MODULATOR TOPOLOGY
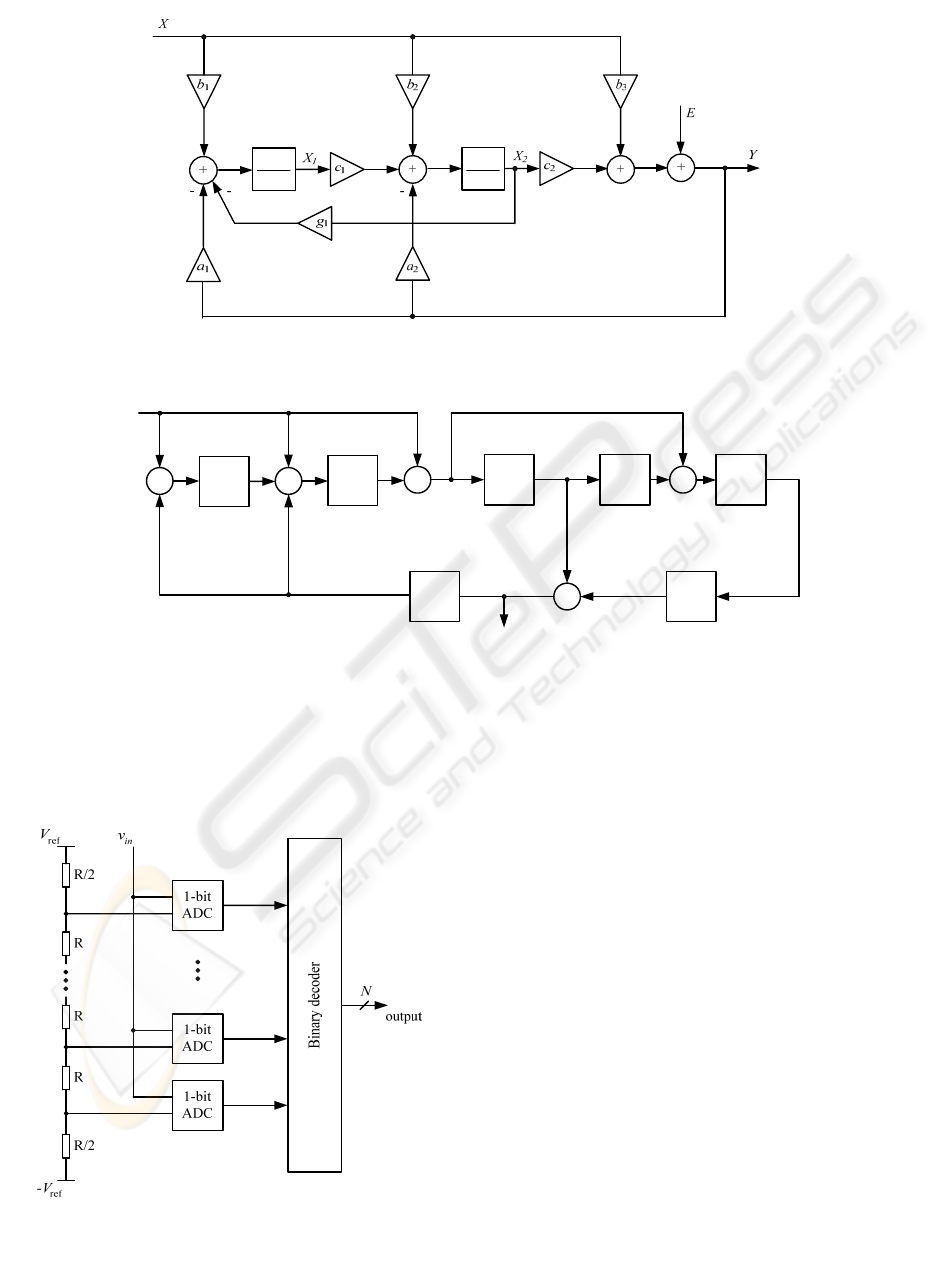
Proposed Architecture. New proposed architecture
of sigma-delta modulator is derived from CIDIDF
second order sigma-delta modulator (Fig. 1).
Multibit ΣΔ modulator with two-step quantization
process (Fig. 2) is based on dividing the AD
142
Fujcik L., Vrba R. and Sveda M. (2006).
A 16-BIT SWITCHED-CAPACITOR SIGMA-DELTA MODULATOR MATLAB MODEL EXPLOITING TWO-STEP QUANTIZATION PROCESS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 142-147
DOI: 10.5220/0001207901420147
Copyright
c
SciTePress
conversion into two steps, which makes the internal
quantization feasible with much higher resolution
than with conventional solution. The all operations,
like integration, AD and DA conversions have to be
executed at the same time in ΣΔ modulators. If any
operation takes significantly longer time than the
others, it will limit the speed and consequently
dynamic range. A flash-type converter with M-bits
resolution performs the first coarse conversion
(ADC1). Difference between the coarse conversion
result and the sampled loop filter output is amplified
by the DAC, and the error is AD converted by an N-
bit flash converter ADC2. The outputs from two
stages are added digitally, resulting in feedback
word M+N bits (
Lindfors et al., 2001).
Expressions of STF and NTF are written as
()
1
2
1
1
2
0
11
1
g
NTF z a
a
−
=
⎧
⎫
⎪
⎪
=
−⇔=
⎨
⎬
⎪
⎪
=
⎩⎭
,
11
22
3
1
1
ba
STF b a
b
=
⎧⎫
⎪⎪
=⇔ =
⎨⎬
⎪⎪
=
⎩⎭
(1)
Internal ADC1 and ADC2 are represented by
flash-type converters (Fig. 3). Each N-bit flash-type
converter needs 2
N
-1 comparators. For example, an
8-bit flash ADC requires 255 comparators. The
same resolution can be achieved with a total of only
30 comparators (4+4 bits). In today’s technologies,
1
1
1
z
−
−
1
1
1
z
z
−
−
−
Figure 1: CIDIDF second order sigma-delta modulator.
H(z)
ADC1 DAC ADC2+
2
-M
+
+
X
Y
M
N
DAC
M+N
-
-
+
H(z)
+
--
Figure 2: A multibit ΣΔ modulator with two-step quantization process.
Figure 3: Flash-type converter with an input digital latch
ΣΔ converter specification.
A 16-BIT SWITCHED-CAPACITOR SIGMA-DELTA MODULATOR MATLAB MODEL EXPLOITING TWO-STEP
QUANTIZATION PROCESS
143

8-bit converters having a reasonable die size and
consuming moderate power are available. For
example, increasing the resolution to 10 bits
increases the die size and power dissipation roughly
four times. In practice, there is a limit to the power
dissipation at the same level as the 8-bit unit.
ΣΔ modulator nonidealities. The main
nonidealities of this circuit which are considered in
this paper are the following (Bourdopoulos et al.,
2003), (Malcovati et al., 2000): clock jitter at input
sampler, switch thermal noise in the SC structure,
operational amplifier noise, operational amplifier
finite gain, operational amplifier BW, operational
amplifier SR, operational amplifier saturation
voltages.
Table I: ΣΔ converter specifications.
Parametr Value
Signal bandwidth 100 kHz
Sampling frequency 16 MHz
Oversampling ratio 64
Modulator order 2
Number of bits of internal quantizer 4 + 4
Bit resolution 16
The use of the SC technique for the
implementation means that all the blocks in an SC
ΣΔ modulator are properly synchronized. Using the
building blocks presented in the following sections,
the simulation of any SC ΣΔ modulator is possible.
The basic concept of the proposed simulation
environment is the evaluation of the output samples
in the time domain. The nonidealities listed above
produce a deviation of the output samples from their
ideal values. The overall performance of the ΣΔ
modulator is then evaluated in the frequency domain
after proper fast Fourier transform (FFT) of the
output samples.
3 TWO-STEP QUANTIZER
Proposed architecture. To avoid some of problems
encountered with a full-flash converter, the two-step
architecture was developed (Fig. 4). This two-step
method uses a coarse and fine quantization to
increase the resolution of the converter (Van de
Plassche et al., 2003).
Accuracy issues related to the two-step internal
quantizer. The overall accuracy of the converter is
dependent on the first ADC. The second flash
should have only the accuracy of a stand-alone Flash
converter. This means that an 8-bit two-step internal
quantizer contains two 4-bit Flash converters, the
Figure 4: Two-step internal quantizer.
+
ADC
DAC
-
ADC
DAC
+
IN
OUT
Κ
1
Κ
2
Κ
4
Κ
3
N/2
N/2
N
d
Figure 5: Model of two-step internal quantizer.
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
144

second Flash needs only to have the resolution of a
4-bit, which is not difficult to achieve.
Figure 6: Symbol of two-step internal quantizer.
However, the first 4-bit Flash should have the
accuracy of an 8-bit Flash, meaning that the worst-
case INL and DNL for the first bit Flash must be
less then ±½ LSB for an 8-bit ADC. Thus, the
resistor matching and comparators contained in the
first ADC must posses the accuracy of the overall
converter. The DAC must also be accurate to within
the resolution of the ADC.
MATLAB model of two-step internal quantizer.
The model of two-step quantization converter bit is
shown in Fig. 5. This model of two-step
quantization converter was designed and simulated
in MATLAB SIMULINK. The symbol of two-step
quantization converter is shown in Fig. 6.
Constants (2) have to be correctly set for two step-
quantization process.
1
2
1
2
N
K = ,
2
2
2
N
K = ,
3
2
1
2
N
K = ,
4
2
1
1
1
2
N
K =
+
(2)
Simulation and results. 4-bit resolution of two-step
quantization converter is shown in Fig. 7. (N=4)
Figure 7: Simulation results of two-step internal
quantizer (4-bit resolution).
a)
b)
Figure 9: Output spectrum of novel multibit SC ΣΔ
modulator with two-step quantization process (N=8).
a) Ideal model, b) real model.
A 16-BIT SWITCHED-CAPACITOR SIGMA-DELTA MODULATOR MATLAB MODEL EXPLOITING TWO-STEP
QUANTIZATION PROCESS
145
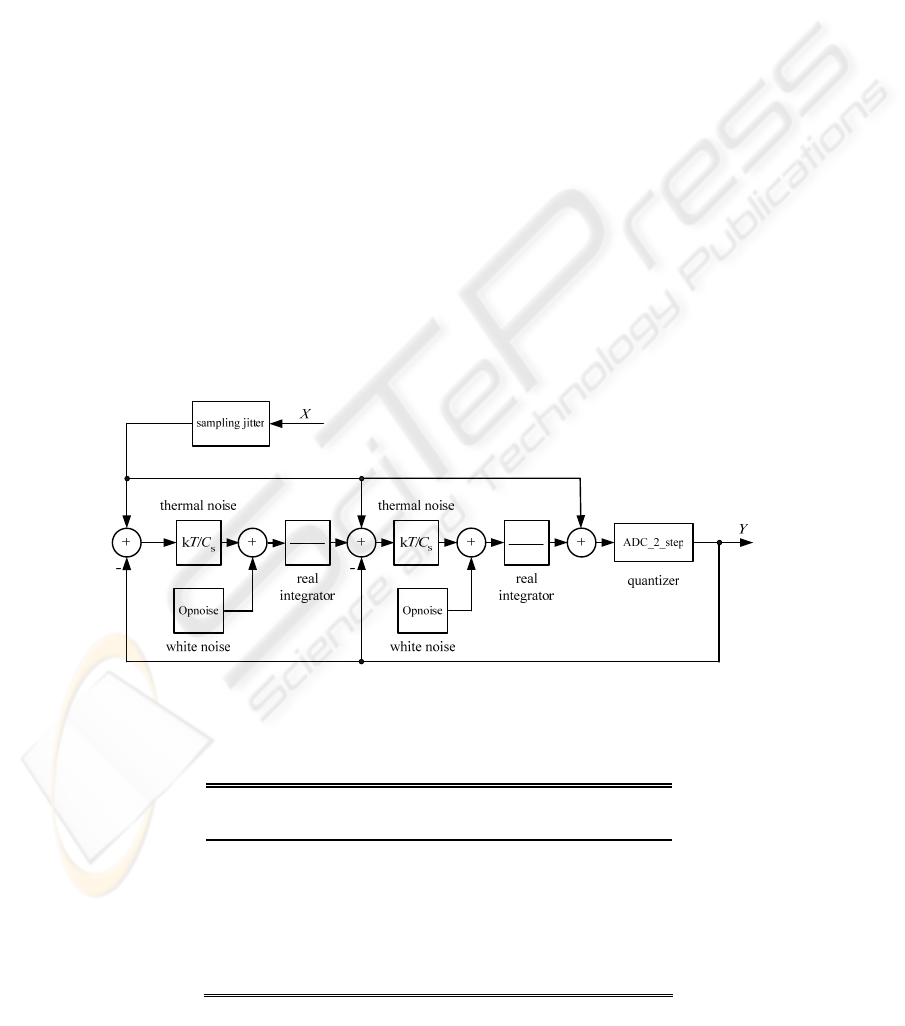
4 MATLAB MODEL OF
MODULATOR
Model topology. Real model of novel multibit SC
ΣΔ modulator with two-step quantization process is
shown in Fig. 8.
Simulation and results. The internal resolution of
two-step quantization converter was set to 8 bits
(4+4 bits) for all calculation of SNR. Output
spectrum of proposed modulator is shown in Fig. 9.
5 CONCLUSION
In this paper, we presented a model of proposed ΣΔ
modulator implemented in the MATLAB
SIMULINK environment suitable for time domain
behavioral simulations of SC ΣΔ modulators.
Specification of the ΣΔ converter is shown in
TABLE I. The output resolution requirement of ΣΔ
converter is 16 bits. We obtained ENOB = 16.38
bits while modeling of real model of novel SC ΣΔ
modulator with two-step quantization process
including all nonidealities. ΣΔ converter
requirements were realized. The comparison of ideal
and real model of novel sigma-delta architecture is
described in this paper.
The next step will be a design and modeling of
novel SC ΣΔ converter in CMOS 0.35 μm
technology in CADENCE software. In future we
will use compensation technique CDS in switched-
capacitor integrator design and dynamic element
matching in DA converters design for two-step
quantization converter.
ACKNOWLEDGMENTS
The research has been supported by the Czech
Ministry of Education in the frame of Research
Program MSM0021630503 MIKROSYN, by the
Czech Grant Agency as the GA102/05/0869 project
AD and DA Converters and GA102/03/H105
project.
1
1
1 z
−
−
1
1
1
z
z
−
−
−
Figure 8: Real model of novel multibit SC ΣΔ modulator with two-step quantization process.
Table II: SNR and resolutuion of SC ΣΔ modulator with two-step quantization process (n = 8).
Modulator parametr
SNR
[dB]
ENOB
[bits]
ideal model 112,1 18,33
thermal noise (Cs = 2,5 pF) 103,0 16,81
sampling jitter (τjit = 220 ps)
107,5 17,57
white noise (V
n
= 34 mV) 104,1 17,01
finite DC gain (H
0
= 104) 108,9 17,80
slew rate (SR = 0,5μV)
109,5 17,90
finite gain bandwidth (GBW = 2 MHz) 109,7 17,93
real model with all nonidealities 100,3 16,38
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
146

REFERENCES
Lindfors, S., Halonen, K. A. I., 2001. Two-step
quantization in multibit ΔΣ modulators. In IEEE
Transactions on Circuits and Systems II: Analog and
Digital Signal Processing. Vol. 48, no. 2, p. 171 –
176, ISSN 1057-713.
Ifeachor, E. C., Jervis, B. W., 2002. Digital Signal
Processing – A practical approach. The book, Pearson
Education Limited. Edinburgh Gate, 2
nd
edition.
Lindfors, S., Halonen, K. A. I., 2000. Two-Step
Quantization Architectures for Multibit DS-
Modulators. In International Symposium on Circuits
and Systems. Geneva, Vol. 2, p. 25 – 28.
Norsworthy, S. R., Schreier, R., Temes, G. C., 1997.
Delta-Sigma Data Converters. Theory, Design, and
Simulation. IEEE Press Marketing. ISBN 0-7803-
1045-4.
Bourdopoulos, G. I., Pnevmatikakis, A., Anastassopoulos,
A., Deliyannis, T. L., 2003. Delta-Sigma
Modulators: Modeling, Design and Applications.
Imperial College Press. ISBN 1-86094-369-1.
Mualik, P. C., Chadha, M. S., Lee, W. L., Crawley, P. J.,
2000. A 16-Bit 250-kHz Delta–Sigma Modulator and
Decimation Filter. In IEEE Journal of Solid-State
Circuits. Vol. 35, no. 4, p. 458-467.
Malcovati, P., Brigati, S., Francesconi, F., Maloberti, F.,
Cusinato, P., Baschirotto, A., 2003. Behavioral
Modeling of Switched-Capacitor Sigma–Delta
Modulators. In IEEE Transactions on Circuits and
Systems I: Fundamental theory and applications. Vol.
50. ISSN 1057-7122, p. 352-364.
Fujcik, L., Kuncheva, A. S., Mougel, T., Vrba, R., 2005.
New VHDL Design of Decimation Filter for Sigma-
delta Modulator. In International Conference On
Sensors and International Conference on New
Techniques in Pharmaceutical and Biomedical
Research. Asiasense 2005, IEEE Malaysia Section,
Malaysie, ISBN 0-7803-9371-6.
Van de Plassche, R., 2003. CMOS Analog-to-Digital and
Digital-to-Analog Converters. The book, Kluwer
Academic Publishers, 2
nd
edition.
A 16-BIT SWITCHED-CAPACITOR SIGMA-DELTA MODULATOR MATLAB MODEL EXPLOITING TWO-STEP
QUANTIZATION PROCESS
147
