
USING THE TRANSFERABLE BELIEF MODEL TO VEHICLE
NAVIGATION SYSTEM
Khalid Touil, Mourad Zribi and Mohammed Benjelloun
Université du Littoral Côte d’Opale, Maison de la recherche Blaise Pascal,
Laboratoire d’Analyse des Systèmes du Littoral, (LASL-EA 2600),
50, rue Ferdinand Buisson, B.P. 699, 62228 Calais Cedex, France.
Keywords: Global Positioning System, Dead Reckoning, a map-matching method, Transferable Belief Model.
Abstract: In general, navigation systems estimating a vehicle position is done either by using the Global Positioning
System (GPS) or the Dead Reckoning (DR) systems. Other modern estimations are based on the
combination of the two systems (GPS/DR). However, the position of a vehicle determined by GPS/DR is far
from being perfect since it produces many errors. To solve this problem, a map-matching method is
proposed in order to reduce the errors of localization caused by GPS/DR. This algorithm, which uses a
digital road map, allows the detection of the correct road where a vehicle moves. In this paper, we introduce
a new map-matching algorithm that employs the Transferable Belief Model (TBM). The TBM presents a
general justification of belief theory and provides a flexible and adapted representation for the measured
beliefs. Experimental results show the effectiveness of the utilization of the TBM to the vehicle navigation
system.
1 INTRODUCTION
The car navigation systems promise to be a valuable
aid for traveler’s drivers of vehicles who need to
reach a variety of destinations as quickly and
efficiently as possible. The main role of a car
navigation system is to find the car position as
precisely as possible. The Global Positioning System
(GPS) sensor is the most attractive one. This is
because the position can be calculated on the globe
if more than four satellites are detected (Parkinson,
1996). Nevertheless GPS suffers from satellite
masks occurring in urban environments, such as
under bridges, tunnels, etc. GPS appears then as an
intermittent positioning system that demands the
help of a DR system. This last estimates the position
by integrating the displacements at every sampling
time. Since this method is subject to major
accumulation of errors caused by wheel slippage,
surface roughness, etc.
In our work, we use the odometer sensor. We
integrate GPS with odometer by employing a
Kalman filter (Chui, 1991; Zhao, 2003). The
estimated position by Kalman filter is proved to be
optimal if the system is linear and the noise is white
Gaussian (Grewal, 1993). It should be noted that as
the noise of the GPS is not white Gaussian and the
system is not linear, the estimated position from
Kalman filter is not optimal. It leads to position
errors. To reduce the error, we suggest using a map-
matching approach (Bernstein, 1998; Greenfeld,
2002). It is a method of using digital map data and
integrated GPS/odometer to locate the vehicle on
proper road relative to digital map. Conventionally,
map-matching is performed using either a geometric
approach or a statistical approach. Geometric map-
matching, as the name suggests, is based on pure
geometric criteria identifying the road segment on
which the vehicle is traveling (Lee, 1998). Statistical
map-matching, is based on curve fitting onto a road
network based on the history of motion (Hummel,
2005). It uses a conditional probability (Taylor,
2001). In this paper, we present a new map-
matching method. This method provides an accurate
position of a vehicle relatively to a digital road map
using the TBM and the Kalman filter. The TBM is a
model that represents quantified beliefs based on the
use of belief functions, as initially proposed by
Shafer (Dempster, 1967; Shafer, 1976). This map-
10
Touil K., Zribi M. and Benjelloun M. (2006).
USING THE TRANSFERABLE BELIEF MODEL TO VEHICLE NAVIGATION SYSTEM.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 10-17
DOI: 10.5220/0001209300100017
Copyright
c
SciTePress

matching method is composed on four steps. Firstly,
a Kalman filter fuses the GPS and the odometric
measurements to estimate a position of the vehicle.
Secondly, we use the estimated position and the
variance-covariance information given by Kalman
filter in order to define a zone in which
Geographical Information System (GIS) will use it
and we preselect the segments on which the vehicle
is likely to be. Thirdly, we select among the
candidate segments the most credible segment one
using the TBM. Finally, we build a map observation
starting from the most credible segment then to
integrate it, in the formalism of Kalman as a second
equation of observation. Here, we are interested in
the second and the third steps of this method which
represent our contribution.
The paper is organized as follows. In section 2, we
recall the main concepts of Belief theory and their
interpretation in the setting of TBM. In section 3, we
present the adaptation of this model for the segment
selection problem. Finally, experimental results will
be presented in section 4.
2 THE TRANSFERABLE BELIEF
MODEL
The Transferable Belief Model (TBM) provides a
flexible and very powerful representation of
quantified beliefs. The model was introduced by
Smets (Smets, 2002) and based on the belief
function theory developed by Shafer (Shafer, 1976).
But, it is completely unrelated for any underlying
probabilistic constraints as it is the case with the
model of Dempster (Dempster, 1967) and for the
hint model (Kohlas, 1995). In the TBM, two-level
model for belief has been proposed: a credal level
where belief is entertained, and a pignistic level
where beliefs are used to make decisions.
2.1 Credal Level: Modeling of
Knowledge
At the credal level, belief is quantified by belief
functions. Let
Θ be a finite set of elements called
the frame of discernment. It is composed of mutually
exclusive elements called hypotheses. By definition,
the mapping bel:
Θ →[0,1] is a belief function if
and only if there exists a basic belief assignment
function (bba) m:
m:
Θ
2
→[0,1] (1)
such that:
0)( 1)(
1
,
===
=Θ⊆∀
∑
∑
≠⊆
⊆
φ
φ
belm(B)Abel
m(A)A
BAB
ΘA
(2)
The values m(A), are called the basic belief mass and
represent the minimal (necessary) support for A and
cannot be associated with any of the sub-
propositions on the basis of available evidence
(Smets, 1994). The belief (bel(A)) of a proposition
A is therefore a sum of all the belief masses
allocated to sub-propositions B. If further the piece
of evidence brought by a source of information
(sensor, agent, etc) shows that
AB ⊆
is true, then
the belief mass
m(A) initially allocated to A is
transferred to
B
A
∩
that is where the name of
TBM comes from. So far we assumed that only one
of the propositions in
Θ
is true (“close-world”
assumption) this can be generalized by letting that
none of the propositions considered in
Θ could be
true (“open-world”). In this case, a positive basic
mass can be given to an empty set
φ
. The term )m(
φ
represents a degree of belief that cannot be given to
any of the propositions in
Θ . The conjunctive rule
of combination of two pieces of evidence on
Θ
represented by the two bba m
1
and m
2
is:
)()()(
2121
Θ⊆∀=⊕
∑
=∩
ACmBmAmm
ACB
(3)
)()()(
2121
∑
=∩
=⊕
φ
φ
CB
CmBmmm
(4)
The value
)(
21
φ
mm ⊕
represents the incoherence
between the different sources of information. It can
be interpreted as a measure of the conflict between
the sources.
2.2 Pignistic Level: Decision Making
At the pignistic level, belief is quantified by
probability functions. For most applications, a
decision is generally, to be taken in favor of a simple
hypothesis. Within the context of the TBM, Smets
defines and justifies the use of the pignistic decision
rule (Shafer, 1976; Smets, 1994). Let
BetP be the
pignistic probability distribution derived from the
basic belief assignment (bba)
m. BetP is defined by:
USING THE TRANSFERABLE BELIEF MODEL TO VEHICLE NAVIGATION SYSTEM
11

))(1)((
)(
)( Θ∈
∑
∈
∀
−
=
A
mAcard
Am
BetP
ω
ω
φ
ω
, (5)
where
card(A) is the cardinality of A.
3 SELECTION METHOD OF
SEGMENT
Vehicle tracking on a given road segment is known
as map-matching (Bernstein, 1998; Greenfeld,
2002). Indeed to localize oneself on a network road,
it is necessary first of all to select the segment on
which the vehicle is actually traveling (Zhao, 1997).
In literature, there are many techniques of selection.
Such as the method proposed by (El Najar, 2005)
which fuses two criteria using Belief theory. Each of
these criterions is characterized by belief function.
In this paper, we propose a method of estimation
treating these belief functions more explicitly than
proposed in (El Najar, 2005). This proposition
allows the reduction of both the position errors (see
figure 6.d) and the conflict (by the addition of a
factor of weakening or discounting see Eq. 9 and Eq.
11) computed in the Dempster-Shafer fusion rule.
3.1 Preselection of the Road
Segments
The first step is to determine which road segments
are candidates for the localization of the vehicle. For
this, the basic characteristic of our algorithm is the
use of an elliptical confidence region around an
estimated position based on error models which are
associated with GPS and odometer sensors. Road
segments that are within the confidence region are
taken as the pseudo candidate segments. These ones
represent the frame of discernment in TBM. If the
confidence region does not contain any segment,
then, it is assumed that the vehicle is not on a
cartographic road. In such a situation, the derived
positions GPS/odometer are used as the final
locations of the vehicle. Many methods are available
for calculating the error region around a fixed
position. Variance-covariance information
associated with GPS receiver outputs is often used to
define an error ellipse. According to (Zhao, 1997),
the error ellipse can be derived as:
222222
4)()(2/1
xyyxyx
ka
σσσσσ
++++=
(6)
222222
4)()(2/1
xyyxyx
kb
σσσσσ
+−−+=
(7)
))
2
arctan((2/1
22
yx
xy
σσ
σ
πγ
−
−=
(8)
where
2
x
σ
and
2
x
σ
are the positional error
variances from the integrated GPS/odometer,
xy
σ
is
the covariance,
a, b are the semi-major axis and
semi-minor axis of the ellipse, γ is the orientation of
the ellipse relative to the North, and k is the
expansion factor. The expansion factor
k is a term
that compensates for the errors associated with GPS,
odometer and digital roadmap sensors. For
simplicity, an error circle can be used instead the
error ellipse. The centre of the circle is the estimate
of the current position and radius
R of this one is
equal to the semi-major axis
a (R=a). The road
segments obtained, thus, form our frame of
discernment
{
}
n
SegSegSeg ,........,,
21
=
Θ
or n is the
total number of the pseudo candidate segments. In
order to select the good road segment up on which a
vehicle moves, we propose a method of selection
based on the Transferable Belief Model (TBM).
3.2 The Proposed Selection Method
The proposed selection method is based on the
fusion of two criteria (proximity and bearing) using
the TBM. The frame of discernment is then
{
}
n
SegSeg ,........,,
1
=
Θ
. In this section, we present the
proximity and the bearing criteria.
1) Proximity criterion: The proximity criterion is
essentially, based on the measure of the Euclidian
distance lying between the estimated position and
each pseudo-candidate segment. Being given the
estimated position
j
P , the belief assignment function
that characterizes this criterion can be obtained as
follows:
⎪
⎩
⎪
⎨
⎧
−−=Θ
−=
∑
=
n
i
ijproximityj
ijproximityji
RdPm
RdPSegm
1
1
1
)/exp(1)/(
)/exp()/(
α
α
(9)
with
proximity
α
is the normalized factor given by:
ICINCO 2006 - ROBOTICS AND AUTOMATION
12

)(/ Θ= card
proximityproximity
β
α
(10)
where
)(Θcard
is the cardinality of Θ and
proximity
β
(
10 ≤≤
proximity
β
) represents the confidence to the
proximity criterion: it reflects our a priori knowledge
on the quality of the GPS and the odometer sensors.
R is the radius of the circle of preselection of the
road segments and
ij
d the distance between the
estimated position
j
P and the candidate segment
i
Seg
.
The distance
ij
d
corresponds to the minimal
distance among the three distances specified in
Figure 1.
Let
j
θ
the estimate of the heading of the vehicle,
and then the belief assignment function
2
m
which
characterizes this criterion is defined by:
[]
[]
(11)
))tan((exp1)/(
))tan((exp)/(
1
2
2
2
2
⎪
⎩
⎪
⎨
⎧
−−−=Θ
−−=
∑
=
n
i
jibearingj
jibearingji
am
aSegm
θαθ
θαθ
where
bearing
α
is the normalized factor defined by:
)(/ Θ= card
bearingbearing
β
α
(12)
which
bearing
β
(
10 ≤≤
bearing
β
) represents the
confidence to the bearing criterion: that value
depends essentially on the speed (Figure 2); and
i
a
is the bearing factor of the segment
i
Seg
.
This way of affecting the belief assignment function
is known under the name of "separate sources"
(
Denoeux, 1997).
Figure 1: Distance between the point and the segment.
2) Bearing criterion: The fusion of GPS and
odometer sensors by Kalman filter provides an
estimate of the probable direction of a vehicle which
would be relevant for the quantification of bearing
criterion. The difference between the heading of a
vehicle and the corresponding value from each
pseudo-candidate segment is used to formulate a
new belief assignment function.
Figure 2: Confidence of the bearing criterion.
In Figure 2, V_threshold represents the threshold of
the speed above of which the bearing criterion is
reliable. That value is determined by the
experimental tests.
3) Fusion and decision: According to the two
criteria, we are in the presence of two belief
assignment functions
1
m
and
2
m
. We apply the
conjunctive rule of combination (Eq. 3) in order to
determine a single belief assignment function which
results from the aggregation of these two assignment
functions. Next, we calculate the conflict given by
Eq. 4. If the conflict is lower than 0.5, we calculate
the pinistic probability (Eq. 5), then we choose the
segment which represents the maximum probability.
If it is higher than 0.5, it is not possible to make a
decision.
The choice of threshold 0.5 is obtained through the
following steps: first, we have simulated many
routes given in Figure 3.a, second, we have tested
our algorithm with different threshold values which
vary between 0.1 up to 0.9, and third, we have
calculated the rate average of selection for each
threshold (see Figure 3.b). According to Figure 3.b,
we notice that threshold 0.5 represents a better
solution in term of rate average of selection 85 %.
bearing
β
1
S
p
eed
V_threshold
1
d
2
d
3
d
j
P
1
d
2
d
2
S
P
j
P
2
S
P
1
S
P
USING THE TRANSFERABLE BELIEF MODEL TO VEHICLE NAVIGATION SYSTEM
13

Figure 3.a: Simulation of many routes.
Figure 3.b: The variation of the rate average of selection according to the thresholds.
ICINCO 2006 - ROBOTICS AND AUTOMATION
14
4 EXPERIMENTAL RESULTS
For the testing of the algorithm, a comprehensive
field test was carried out in Calais (France). A test
vehicle was equipped with a navigation platform
consisting of a 12-channel single frequency GPS
receiver (ProPak-G2), the interfaces require to be
connected to the vehicle Speed sensor (odometer)
and to the digital road map which is used as a
reference that had a resolution of 3.5m. The duration
of collecting data was about 1hr. As already
mentioned, the purposed algorithm is developed in
two steps: the first step is to seek the road segment
where the vehicle moves, and the second step is to
determine the vehicle location on that road segment.
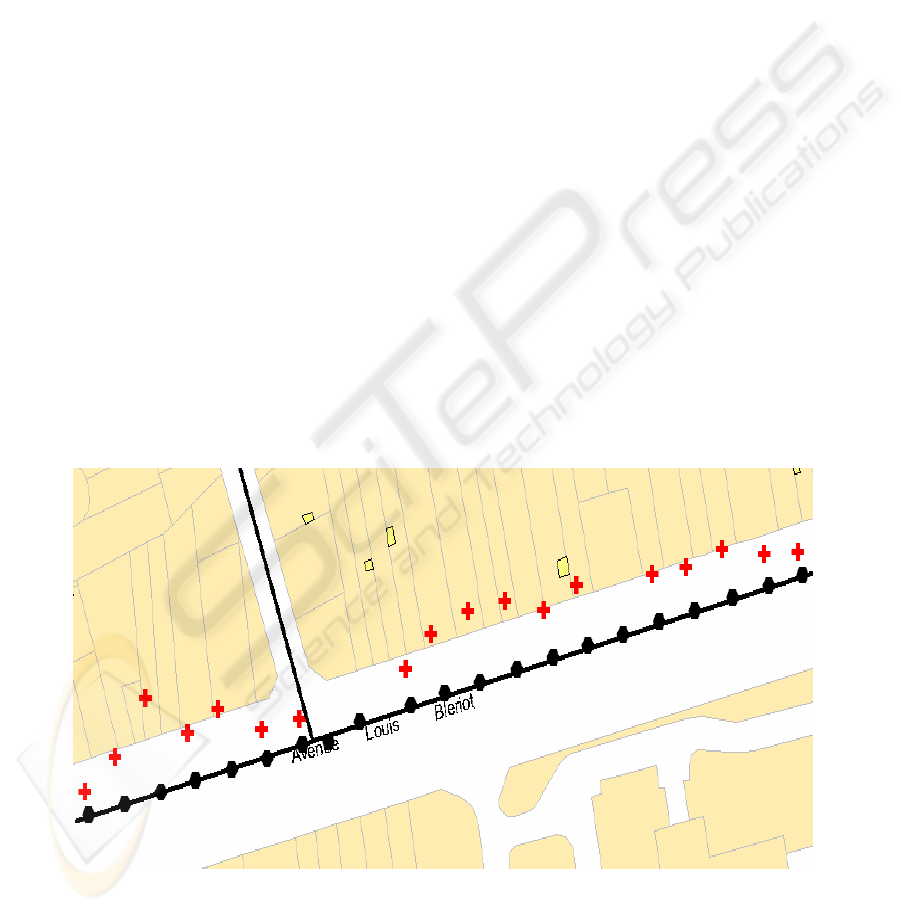
Figure 4 illustrates the results of the algorithm for
the sample routes. The symbols + (red) and o (black)
respectively represent the vehicle position before
and after the application of the algorithm.
In order to evaluate the performance of our
algorithm, we take the case of a problematic
situation standard for example a junction of two
roads (Figure 5). In this figure the circle presents the
zone of preselection that contains three segments
(Seg1, Seg2 and Seg3) which define our frame of
discernment. The two belief assignment functions
which characterize the proximity criterion and the
bearing criterion are defined on this frame.
The figures (Figure 6.a, Figure 6.b, and Figure 6.c)
represent a variation of belief assignment functions
within this frame of discernment. The proximity
criterion (Figure 5.a)
shows that the Seg2 is the most
credible. The bearing criterion (Figure 5.b) affirms
that the segments Seg1 and Seg2 are the most
credible. The combination of both criteria (Figure
5.c) confirms that Seg1 and Seg3 are the most
credible. Such an ambiguous situation can be
resolved if we take into account the information that
Seg1 and Seg3 represent the same road.
Figure 6.d shows the variation of error sigma
(northing) with time for both the integrated
GPS/odometer and the proposed algorithm. The
error sigma associated with the integrated
GPS/odometer is much higher than that associated
with the proposed algorithm. The average standard
deviation before the application of the algorithm is
10 to 15m whereas it is 3 to 4m after its use.
Figure 4: The results of the sample routes.
USING THE TRANSFERABLE BELIEF MODEL TO VEHICLE NAVIGATION SYSTEM
15

Figure 5: Candidates segments at a given moment.
Figure 6.a: Proximity criterion. Figure 6.b: Bearing criterion.
Figure 6.c: Combination of the two criteria. Figure 6.d: Comparison of error sigma.
5 CONCLUSION
In this paper, an algorithm based on the Transferable
Belief Model (TBM) has been developed. This
algorithm has proved to be very efficient, particularly
in difficult operational environments such as
junctions and intersections. In fact, it can be
considered as an excellent tool to quantify the
ambiguousness of a situation. This work has as a
prospect to develop other criteria in order to treat the
ambiguous situations efficiently (for example
problematic situation of two 2 parallel roads).
REFERENCES
Bernstein D. and Kornhauser A., 1998. Map matching for
personal navigation assistants, The Transportation
Research Board, 77
th
Annual Meeting Washington.
ICINCO 2006 - ROBOTICS AND AUTOMATION
16

Chui C.K. and Chen G., 1991. Kalman filtering with real-
time applications, Springer Verlag, second edition.
Dempster A. P., 1967. Upper and lower probabilities
induced by a multivlued mapping, Annals of
Mathematical Statistics, AMS-38, pp. 325-339.
Denoeux T., 1997. Application du modèle des croyances
transférables en reconnaissance de formes, Traitement
du Signal, Vol. 14, n° 5, 443-451.
El Najjar M. and Bonnifait P., 2005. A road-matching
method for precise vehicle localization using belief
theory and Kalman filtering, Autonomous Robots 19,
173-191.
Greenfeld J. S., 2002. Matching GPS observations to
locations on a digital map, Proceeding of the 81th
Annual Meeting of the Transportation Research Board,
Washington D. C.
Grewal M. S. and Andrew A. P., 1993. Kalman Filtering:
Theory and Practice, Englewood Cliffs, NJ: Prentice-
Hall.
Hummel B., Tischler K., 2005. GPS-only Map Matching:
Exploiting Vehicle Position History, Driving
Restriction Information and Road Network Topology in
a Statistical Framework, In Proc. GIS Research UK
(GISRUK), S. 68-77.
Kohlas J. and Monney P. A., 1995. A Mathematical Theory
of Hints: An Approach to Dempster-Shafer Theory of
Evidence, Lecture Notes in Economics and
Mathematical Systems No. 425. Springer-Verlag.
Lee B. C., 1998. A study on the correction of positioning
accuracy of car navigation system and map matching
algorithm, in Proc. of 5th World Congr. Intelligent
Transport Systems, Seoul, Korea.
Parkinson B. W. and al., 1996. Global Positioning System,
Theory and Applications, American Inst, Aeronautics
and Astronautics.
Shafer G., 1976. A mathematical theory of evidence, Vol.
2702. Princeton University Press.
Smets P. and Kennes R., 1994. The Transferable Belief
Model, Artificial Intelligence, 66, pp. 191-234.
Smets P., 2002. Decision Making in a Context where
Uncertainty is Represented by Belief Functions,
Physica-Verlag, Heidelberg, Germany, 17-61.
Smets P., 2005. Decision making in the TBM: the
Necessity of the Pignistic Transformation, International
Journal of Approximate Reasoning, pp. 133–147.
Taylor G., Blewitt G., Steup D., Corbett S., Car A., 2001.
Road reduction filtering for GPS-GIS navigation, Proc.
of 3
rd
AGILE Conference on Geographic Information
Science, Helsinki, Finland, pp. 114-120.
Zhao L., Ochieng W. Y., Quddus M. A. and Noland R. B.,
2003. An Extended Kalman Filter algorithm for
Integrating GPS and low-cost Dead reckoning system
data for vehicle performance and emissions
monitoring, The Journal of Navigation, 56, pp. 257-
275.
Zhao Y., 1997. Intelligent Transportation Systems: Vehicle
Location and Navigation Systems, Artech House, ISBN.
USING THE TRANSFERABLE BELIEF MODEL TO VEHICLE NAVIGATION SYSTEM
17
