
STEREO DISPARITY ESTIMATION USING DISCRETE
ORTHOGONAL MOMENTS
Tomasz Andrysiak and Michał Choraś
Institute of Telecommunications, University of Technology and Agriculture, ATR Bydgoszcz
Keywords: Stereo Disparity, Discrete Orthogonal Moments, Robotics Vision.
Abstract: In the article we present various theoretical and experimental approaches to the problem of stereo matching
and disparity estimation. We propose to calculate stereo disparity in the moments space, but we also present
correlation based method. In order to calculate disparity vector we decided to use discrete orthogonal
moments of Tchebichef, Zernike and Legendre. In our research of stereo disparity estimation all of these
moments were tested and compared. In the article we also propose the original method of determining the
global displacement vector between the stereopair images in order to find the common part of these images
(adequate for matching) and the margins of these stereo images. Experimental results confirm effectiveness
of the presented methods of determining stereo disparity and stereo matching for robotics and machine
vision applications.
1 INTRODUCTION
One of the main research fields in machine and
robotics vision is 3D scene perception based on
techniques of measuring shapes, positions and
relations between 3D objects that are visible in the
scene. There are many known methods of retrieving
information about the scene basing on 3D perception
(Andrysiak and Choraś, 2005a). Those methods are
based on disparity of stereoscopic scene elements
and on information from the common part of stereo
images. After extracting the pair of corresponding
points in two stereo images, which are related to the
same point in the scene, we can define the difference
between coordinates of those points. Then basing on
such differences, it is possible to create depth map
for the visible scene by means of simple
trigonometric transformations.
Recently discrete orthogonal moments have
gained much attention and have been successfully
used in many applications of computer vision (e.g.
pattern recognition) (Makundan et al., 2002, Lio and
Pawlak, 1996). Therefore in our research we decided
to take advantage of discrete orthogonal moments’
properties in order to calculate stereo disparity.
Therefore in our research we used the discrete
orthogonal moments of Tchebichef, Zernike and
Legendre.
In the article we are concerned with the images
acquired from the axe-parallel robotics vision
system. In such system optical axes of both cameras
are parallel to each other, and image planes of
stereoscopic pair are situated within the same
distance from the centre of the scene coordinates
system. Only the common scene area covered by
both cameras is further analysed (even though it is
only a part of each of the image).
In Section 2 the method of displacement vector
calculation in order to determine the margins and
common part of stereo images is presented. Then in
Section 3 two approaches to calculate stereo
disparity are described. In Sections 4 and 5
experiments and conclusion are given.
2 CORRESPONDENCE
PROBLEM - STEREO
DISPLACEMENT SEARCH
In order to find the displacement vector d
t
between
stereopair images we perform calculation of the
discrete orthogonal moments of right I
P
and left I
L
stereo image.
We search for the displacement vector d
t
by
determining the minimum from the set of values:
504
Andrysiak T. and Chora
´
s M. (2006).
STEREO DISPARITY ESTIMATION USING DISCRETE ORTHOGONAL MOMENTS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 504-507
DOI: 10.5220/0001209805040507
Copyright
c
SciTePress
() ()
)}(,...,1,0{
max
t
dUUU (1)
calculated accordingly to (2) characterizing
adequately subtraction of reconstructed images I
L
and I
P
regarding to maximal displacement vector
d
tmax
:
() ( ) ( )
() ()
∑∑∑∑
∑∑
−
−=
−
=
−
=
−
=
−
=
−
=
++
+−+=
11
0
1
0
1
0
0
1
0
,,
,,
N
dNx
N
y
P
d
x
N
y
L
dN
x
N
y
PtLt
t
t
t
yxIyxI
yxIydxIdU
, (2)
where I
L
(x+d
t,
,y) and I
P
(x,y) can be calculated on the
basis of reconstructed intensity function values, for
the Tchebichef, Legrande and Zernike moments,
respectively (Makundan, 2004).
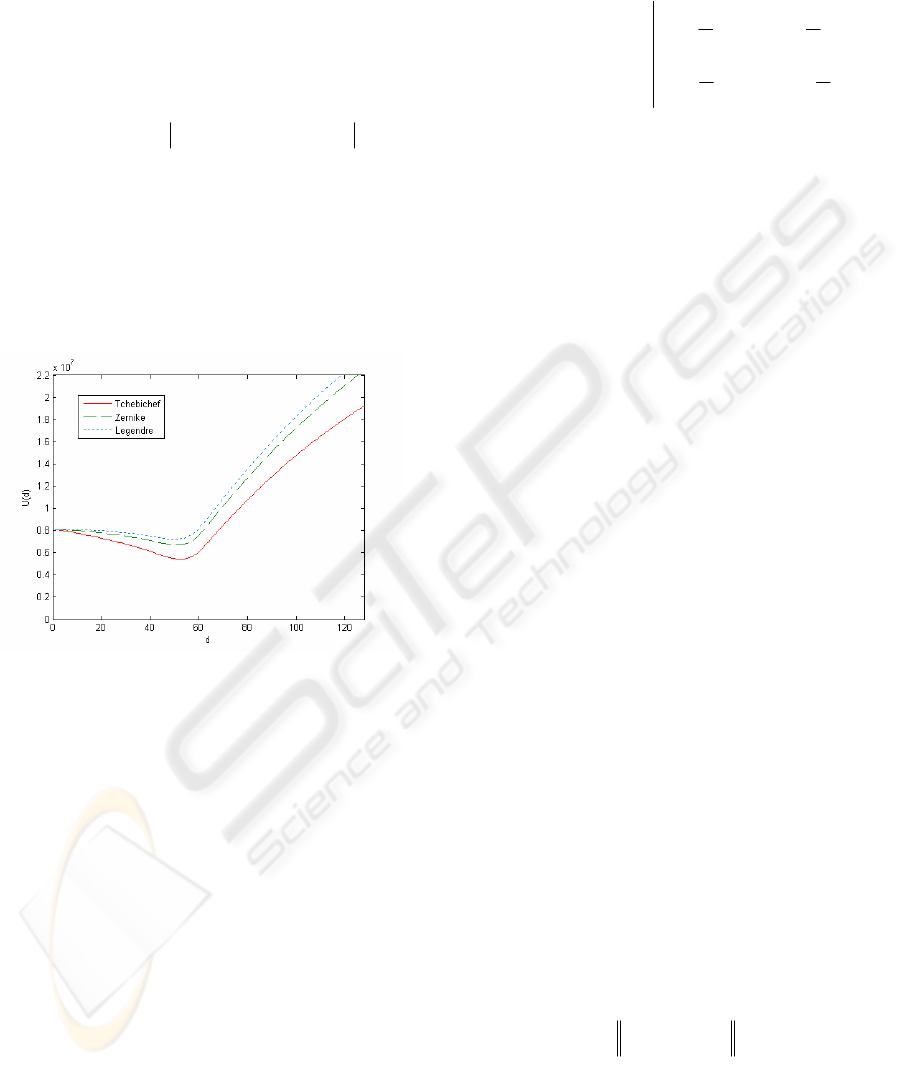
Figure 1: Values of function U(d
t
) for d
t
=0,1,…,128.
3 DISPARITY ESTIMATION
Hereby we present two approaches of solving the
problem of disparity estimation in stereo vision.
These approaches are based on the orthogonal
moments calculation (Mukundan, 2004, Mukundan
et al., 2002)
.
3.1 Stereo Matching Based on
Correlation of Moments
In order to determine the stero disparity d
x
of the
common part of the stereopair, the corresponding
points on the epipolar lines have to be found in the
process of stereo matching.
In practice, in this approach, we search for the
correlation between reconstructed intensity functions
of the images I
L
and I
P
in the regions bounded by the
window function:
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+≤≤−
+≤≤−
=
22
22
,),(
z
yv
z
y
z
xu
z
x
vuyxW
ee
ez
, (3)
where z characterizes the size of window function,
and (u,v) are the coordinates describing the
localization of window W
z
(x,y
e
), where y
e
is the
epipolar line.
The correlation matching process is realized in
the common part of stereopair (determined by the
vector d
t
) according to the following steps:
for each point of the right image I
p
(x,y
e
)
choose its neighbourhood by the window
function W
z
(x,y
e
) where (x,y
e
) is the centre
of the window W
z
,
for all the points from the linear
neighbourhood of the left image I
L
(x)
choose its neighbourhood by the window
function W
z
(x+d
x,
,y
e
) where d
x
characterizes
the stereo disparity interval and d
x
is within
<-d
max
,, d
max
>,
for the determined points and their
neighbourhoods search for the minimum of
the function C
SSD
:
(
)
[
]
∑
∈
+−=
),(),(
2
),(),(
yxWvu
exLePxSSD
z
vduIvuIdC
(4)
The minimum of the C
SSD
function determines the
value of stereo disparity d
x
for the matched points of
the left and right stereopair image.
3.2 Stereo Matching Based on the
Similarity of Vectors in the
Moments Space
An alternative approach to correlation matching
method based on function (4) minimum search can
be similarity search in the feature vector space
according to:
(
)
)()(
min
P
dx
L
x
d
x
x
x
d
+
−=Ψ
λλ
(5)
where
λ
x
(L)
is a vector consisting of moments values
)( L
i
φ
of the intensity function in a given window W
z
STEREO DISPARITY ESTIMATION USING DISCRETE ORTHOGONAL MOMENTS
505

with the centre in point (x,y
e
) on the left image of
stereopair given by:
[
]
),(
)()()(
2
)(
1
)(
,...,...,,
ezi
yxW
L
M
L
i
LLL
x
∈
=
φ
φφφφλ
(6)
and
λ
x+d
(P)
is a vector consisting of moments values
)(P
i
φ
of the intensity function in a given window W
z
with the centre in point (x+d,y
e
) on the right image
of stereopair given by:
[
]
),(
)()()(
2
)(
1
)(
,...,...,,
exzi
x
ydxW
P
M
P
i
PPP
dx
+∈
+
=
φ
φφφφλ
(7)
The similarity measure between the moments is
calculated on the basis of the Euclidean distance.
The obtained minimum of the similarity measure
Ψ(d
x
) determines the stereo disparity d
x
between
points (x,y
e
) on left image and (x+d
x
,y
e
) on the right
stereo image.
4 EXPERIMENTAL RESULTS
In the experiments we used our own stereo images
database of resolution 512×512 and 256 greyscale
levels. All the images were acquired by the well-
calibrated axe-parallel camera system.
Before disparity estimation we calculate the
displacement vector d
t
between image stereopair (we
find the common part of stereo images). This stage
is based on search of the global minimum of the
function U(d
t
) in the interval <0;d
tmax
>, where d
tmax
is set as ¼ of the image resolution.
Figure 2: Stereoscopic image ‘blocks’ with the marked
margins.
Table 1: Displacement vector values.
Reconstraction for
t
d )(
t
dU
Tchebichef 52 0,58
.
10
7
Legendre 59 0,76
.
10
7
Zernike 55 0,71
.
10
7
For sample stereo image ‘blocks’ from our
database (Figure 2), the values of the displacement
vectors d
t
and the values of the function U are
presented in Table 1.
Such situation was caused by imprecise
approximations in the reconstruction formulas and
by the larger sensitivity of Legendre moments on
intensity function deformations in the process of
stereoscopic projections. Moreover the errors were
caused by the high orders of the used moments.
In order to verify the proposed methods of stereo
disparity calculation (sections 5.2-5.3), we use the
normalized disparity error, given by:
()()
max
,
ˆ
,
1
1
0
1
0
x
eex
N
y
N
x
d
yxdyxd
NN
NDE
−
×
=
∑∑
−
=
−
=
,
(8)
where:
(
)
ex
yxd , is the calculated stereo disparity
in the specified point
(
)
e
yx,
;
()
e
yxd ,
ˆ
is the ideal
stereo disparity calculated by other methods (e.g.
correlation matching) and
max
x
d is the maximal
stereo disparity for the given image.
Due to such formula (8), the normalized stereo
disparity error values are varying within the interval
<0;1>.
In the Figure 2 we presented the influence of the
number of the used moments on the NDE. It
decreases with the larger number of the used
moments. Such situation reflects the impact of
moment order on the reconstruction precision of
image intensity function.
Figure 3: Stereo disparity calculation error on the basis of
the correlation of moments.
The results of stereo disparity estimation method
implementation on the basis of the vectors similarity
in the moments space and an interesting
ICINCO 2006 - ROBOTICS AND AUTOMATION
506

phenomenon of moments order adjustment are
shown in the Fig 2. The obtained value of NDE is
optimal for the moments of order 20-25. Then with
the higher order of moments the results become
worse, which is caused by the increased distance
between vectors (5) in the Euclidean space.
Figure 4: Stereo disparity calculation error on the basis of
the similarity of vectors in the feature space.
5 CONCLUSIONS
In the article we presented the idea and
implementation of using discrete orthogonal
moments of Tchebichef, Legendre and Zernike in
the process of matching and stereo disparity
estimation. In order to optimise those procedures, in
the first stage we extracted the common parts of
stereo images (which is important for matching) and
the margins of stereo images.
In the article two approaches to the problem of
stereo disparity estimation were presented and
tested. The first approach was based on the
correlation analysis of the reconstruction of image
intensity function on the basis of discrete orthogonal
moments. In the second approach the problem of
stereo disparity estimation was solved by similarity
search in the vector space for the calculated
moments characterizing the corresponding points of
stereo images.
In the described methods we used the discrete
orthogonal Tchebichef, Legendre and Zernike
moments. After experiments we concluded that
Tchebichef and Zernike were the most appropriate
for stereo estimation moments, respectively. Much
worse results were achieved by Legendre moments.
REFERENCES
Andrysiak T., Choraś M., Multiresolution Matching and
Disparity Calculation of Stereo Images in Frequency
Domain, Information Extraction and Processing, no. 23
(99), 2005.
Andrysiak Tomasz, Choraś Michał, Stereo Matching for
Robotics Vision, Proc. of International Conference
PELINCEC 2005 (10 pages).
Liao S. X., Pawlak M. On image analysis by moments,
IEEE Trans. Pattern Analysis and Machine
Intelligence, vol. 18, pp. 254–266, Mar. 1996.
Mukundan, R., Image Analysis by Tchebichef Moments,
IEEE Trans. on Image Processing, vol. 10, no. 9, 1357-
1364, 2001.
Mukundan R, Ong S.H., Lee P.A., Image Analysis by
Tchebichef moments, IEEE Trans. on Image
Processing, vol. 10, no. 9, 1357-1364, 2001.
Mukundan, R S. H. Ong, P. A. Lee, Image analysis by
Tchebichef moments, IEEE Trans. on Image
Processing 10 (9) 1357{1364, 2001.
Mukundan R, Pang A., Khee N, Stereo Image Analysis: A
New Approach Using Orthogonal Moments, Proc. Of
Asian Technology Conference in Mathematics, 513-
522, 2002.
Mukundan, R., A New Class of Rotational Invariants
Using Discrete Orthogonal Moments, IASTED
Conference Signal and Image Processing, 80-84,
Hawaii, USA, 2004.
Chong C-W,, Paramesran R, and Mukundan R,
“Translation and Scale Invariants of Legendre
Moments,” Pattern Recognition, vol. 37, no. 1, pp.
119- 129, 2004.
Mukundan R, A new class of rotational invariants using
discrete orthogonal moments, in: Proc. of the 6th
IASTED Int. Conf. on Signal and Image Proc. (SIP'04),
pp. 80-84, 2004.
Mukundan R, “Some computational aspects of discrete
orthonormal moments,”, IEEE Trans. on Image
Processing, vol. 13, no. 8, pp. 1055-1059, 2004.
STEREO DISPARITY ESTIMATION USING DISCRETE ORTHOGONAL MOMENTS
507
