VISUAL SPEECH RECOGNITION USING WAVELET TRANSFORM

AND MOMENT BASED FEATURES

Wai C. Yau, Dinesh K. Kumar, Sridhar P. Arjunan and Sanjay Kumar

School of Electrical and Computer Engineering

RMIT University, GPO Box 2476V Melbourne, Victoria 3001, Australia

Keywords:

Visual Speech Recognition, Motion History Image, Discrete Stationary Wavelet Transform, Image Moments,

Artiﬁcial Neural Network.

Abstract:

This paper presents a novel vision based approach to identify utterances consisting of consonants. A view

based method is adopted to represent the 3-D image sequence of the mouth movement in a 2-D space using

grayscale images named as motion history image (MHI). MHI is produced by applying accumulative image

differencing technique on the sequence of images to implicitly capture the temporal information of the mouth

movement. The proposed technique combines Discrete Stationary Wavelet Transform (SWT) and image mo-

ments to classify the MHI. A 2-D SWT at level 1 is applied to decompose MHI to produce one approximate

and three detail sub images. The paper reports on the testing of the classiﬁcation accuracy of three differ-

ent moment-based features, namely Zernike moments, geometric moments and Hu moments computed from

the approximate representation of MHI. Supervised feed forward multilayer perceptron (MLP) type artiﬁcial

neural network (ANN) with back propagation learning algorithm is used to classify the moment-based fea-

tures. The performance and image representation ability of the three moments features are compared in this

paper. The preliminary results show that all these moments can achieve high recognition rate in classiﬁcation

of 3 consonants.

1 INTRODUCTION

Lip Reading for Human Computer Interface

With the rapid advancement in Human Computer In-

teraction (HCI), speech recognition has become one

of the key areas of research among the computer sci-

ence and signal processing community. Speech driven

interfaces are being developed to replace the conven-

tional interfaces such as keyboard and mouse to en-

able users to communicate with the computers using

natural speech. However, these systems are based on

audio signals and are sensitive to signal strength, am-

bient noise and acoustic conditions.

The human speech production and perception sys-

tem is known to be bimodal and consists of the audio

modality and the visual modality(Chen, 2001). The

visual speech information refers to the movement of

the speech articulators such as the tongue, teeth and

lips of the speaker. The complex range of repro-

ducible sounds produced by people is a clear demon-

stration of the dexterity of the human mouth and lips-

the key speech articulators. This project proposes the

use of video data related to lip and mouth movement

for human computer interface applications. The pos-

sible advantages are that such a system is not sensitive

to audio noise and change in acoustic conditions, does

not require the user to make a sound, and provides the

user with a natural feel of speech and the dexterity of

the mouth. Such a system is termed by the authors as

’Audio-less Speech Recognition’ system.

Audio-less speech recognition requires using only

the sensing of the facial movement. There are a

number of options that have been proposed, such as

visual, mechanical sensing of facial movement and

movement of palate, recording facial muscle activ-

ity(Kumar et al., 2004) and facial plethysmogram.

Speech recognition based on visual speech signal is

the least intrusive and this paper reports such a system

for human computer interface applications.The visual

cues contain far less classiﬁcation power for speech

compared to audio data (Potamianos et al., 2003) and

hence it is to be expected that the visual only systems

would have only a small vocabulary.

Visual speech recognition techniques reported in

the literature in the past decade can be catego-

340

C. Yau W., K. Kumar D., P. Arjunan S. and Kumar S. (2006).

VISUAL SPEECH RECOGNITION USING WAVELET TRANSFORM AND MOMENT BASED FEATURES.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 340-345

DOI: 10.5220/0001209903400345

 SciTePress

rized into two main categories -shape-based and the

appearance-based. The shape-based features rely on

the geometric shape of the mouth and lips and can be

represented by a small number of parameters. One

of the early visual speech recognition system was de-

veloped by Petajan(Petajan, 1984) using shape-based

features such as height, width and area of the mouth

from the binary image of the mouth. Appearance-

based features are derived directly from the pixel in-

tensity values of the image around the mouth area

(Liang et al., 2002; Potamianos et al., 2003).

One common difﬁculty with visual systems is that

these systems are ’one size ﬁts all’ approach. Due to

the large variation in the way people speak, especially

if we transgress the national and cultural boundaries,

these have very high error rate, with error of the order

of 90% (Potamianos et al., 2003). This demonstrates

the inability of these systems to be used for such ap-

plications. What is required is a system that is easy

to train for a user, which works in real-time and be

robust under changing conditions (such as position of

the camera, speed of the speech and skin color.)

To achieve the above mentioned goals, this paper

proposes a system where the camera is attached in

place of the microphone to the commonly available

head-sets. The advantage of this is that using this,

it is no longer required to identify the region of in-

terest, reducing the computation required. The video

processing proposed is the use of accumulative image

differencing technique based on the use of motion his-

tory image (MHI) to directly segment the movement

of the speech articulators. MHI is invariant to factors

such as the skin color and texture of the speakers. This

paper reports the use of 2-D stationary wavelet trans-

form (SWT) at level 1 to decompose the MHI into

four sub images, with the approximate image used for

further analysis. This paper proposes to use image

moments as features extracted from the approxima-

tion of MHI and ANN to classify these features. The

fundamental concept of this technique can be traced

to the research reported by Bobick and Davis(Bobick

and Davis, 2001) in classifying human movement and

the work by Kumar et. al(Kumar and Kumar, 2005)

in hand gesture recognition and biometrics identiﬁca-

tion.

2 THEORY

2.1 Motion History Image

Motion history image (MHI) is a view-based ap-

proach and is generated using difference of frames

(DOF) from the video of the speaker. Accumulative

image difference is applied on the image sequence by

subtracting the intensity values between successive

frames to generate the difference of frames (DOFs).

The delimiters for the start and stop of the motion are

manually inserted into the image sequence of every

articulation. The MHI of the video of the lips would

have pixels corresponding to the more recent mouth

movement brighter with larger intensity values.

The intensity value of the MHI at pixel location (x,

y) of the t

frame is deﬁned by

MHI

= max

N −1

[

t=1

B(x, y, t) × t (1)

N is the total number of frames used to capture the

mouth motion. n represents the B(x,y,t) is the binari-

sation of the DOF using the threshold a and B is given

B(x, y, t) =



1 if Diff(x, y, t) ≥ a,

0 otherwise

(2)

a is the predetermined threshold for binarisation of the

DOF and

Diff(x, y, t) = |I(x, y, t) − I(x, y, t − 1)| (3)

I(x, y, t) represents the intensity value of pixel loca-

tion with coordinate (x, y) at the t

frame of the im-

age sequence. Diff(x, y, t) is the DOF of the t

frame.

In Eq. (1), the binarised version of the DOF is multi-

plied with a linear ramp of time to implicitly encode

the timing information of the motion into the MHI.

By computing the MHI values for all the pixels co-

ordinates (x, y) of the image sequence using Eq. (1)

will produce a scalar-valued grayscale image (MHI)

where the brightness of the pixels indicates the re-

cency of motion in the image sequence(Kumar and

Kumar, 2005).

The motivation of using MHI in visual speech

recognition is the ability of MHI to remove static el-

ements from the sequence of images and preserve the

short duration complex mouth movement. MHI is

also invariant to the skin color of the speakers due to

the DOF process. Further, the proposed motion seg-

mentation approach is computationally simple and is

suitable for real time implementation.

MHI is a view sensitive motion representation tech-

nique. Therefore the MHI generated from the se-

quence of images of different consonants is dependent

on factors such as:

• position of the speaker’s mouth normal to the cam-

era optical axis

• orientation of the speaker’s face with respect to the

video camera

• distance of the speaker’s mouth from the camera

• small variation of the mouth movement of the

speaker while uttering the same consonant

VISUAL SPEECH RECOGNITION USING WAVELET TRANSFORM AND MOMENT BASED FEATURES

341

It is difﬁcult to ensure that the position, orienta-

tion and distance of the speaker’s face are constant

from the video camera for every sample taken. Thus,

descriptors that are invariant to translation, rotation

and scale have to be used to represent the MHI for

accurate recognition of the consonants. The features

used to describe the MHI should also be insensitive

to small variation of mouth movement between dif-

ferent samples of the same consonants. This paper

adopts image moments as region-based features to

represent the approximation of the MHI. Image mo-

ments are chosen because they can be normalized to

achieve scale, translation and rotation invariance. Be-

fore extracting the moment-based features, SWT is

applied to MHI to obtain a transform representation

of the MHI that is insensitive to small variations of

the mouth and lip movement.

2.2 Stationary Wavelet Transform

(SWT)

2-D SWT is used for denoising and to minimize the

variations between the different MHI of the same con-

sonant. While the classical discrete wavelet transform

(DWT) is suitable for this, DWT results in transla-

tion variance (Mallat, 1998) where a small shift of the

image in the space domain will yield very different

wavelet coefﬁcients. SWT restores the translation in-

variance of the signal by omitting the downsampling

process of DWT, and results in redundancies.

2-D SWT at level 1 is applied on the MHI to pro-

duce a spatial-frequency representation of the MHI.

SWT decomposition of the MHI generates four im-

ages, namely approximation (LL), horizontal detail

coefﬁcients (LH), vertical detail coefﬁcients (HL) and

diagonal detail coefﬁcients (HH) through iterative ﬁl-

tering using low pass ﬁlters H and high pass ﬁlters

G. The approximate image is the smoothed version

of the MHI and carries the highest amount of infor-

mation content among the four images. LH, HL and

HH sub images show the ﬂuctuations of the pixel in-

tensity values in the horizontal, vertical and diagonal

directions respectively. The image moments features

are computed from the approximate sub image.

2.3 Moment-based Features

Image moments are low dimensional descriptors of

image properties. Image moments features can be

normalized to achieve translation, rotation and scale

invariance(Mukundan and Ramakrishnan, 1998) thus

are suitable to be used as features to represent the

approximation of MHI.

Geometric moments

Geometric moments are the projection of the image

function f(x, y) onto a set monomial function.The reg-

ular geometric moments are not invariant to rotation,

translation and scaling.

Translation invariance of the features can be

achieved by placing the centroid of the image at the

origin of the coordinate system (x, y), this results in

the central moments. The central moments can be fur-

ther normalized to achieve scale invariant. The nor-

malized central moments are invariant to changes in

position and scale of the mouth within the MHI.

The normalized central moments can be derived up

to any order. In this paper, the 49 normalized geomet-

ric moments up through 9th order are computed from

the MHI as one of the feature descriptors to represent

the different consonants. For the purpose of compar-

ison of the different techniques, the total number of

moments has been kept the same. Zernike moments

require 49 moments, and thus this number has been

kept for the geometric moments as well.

Hu moments

Hu (Hu, 1962) introduced seven nonlinear combina-

tions of normalized central moments that are invariant

to translational, scale and rotational differences of the

input patterns known as absolute moments invariants.

The ﬁrst six absolute moment invariants are used in

this approach as features to represent the approximate

image of the MHI for each consonant. The seventh

moment invariant is skew invariant deﬁned to differ-

entiate mirror images and is not used because it is not

required in this application.

Zernike moments

Zernike moments are computed by projecting

the image function f(x, y) onto the orthogonal

Zernike polynomial. The main advantage of Zernike

moments is the simple rotational property of the

features. Zernike moments are also independent

features due to the orthogonality of the Zernike

polynomial(Teague, 1980). This paper uses the

absolute value of the Zernike moments as the rotation

invariant features(Khontazad and Hong, 1990) of the

SWT of MHI. 49 Zernike moments that comprise of

0th order moments up to 12th order moments have

been used as features to represent the approximate

image of the MHI for each consonant.

2.4 Classiﬁcation using Artiﬁcial

Neural Network

Classiﬁcation involves assigning of new inputs to

one of a number of predeﬁned discrete classes.

ICINCO 2006 - ROBOTICS AND AUTOMATION

342

Figure 1: Block Diagram of the proposed visual speech recognition approach.

There are various classiﬁer choices for pattern recog-

nition applications such as Artiﬁcial Neural Net-

work (ANN), Bayesian classiﬁer and Hidden Markov

Model (HMM). In this paper, we present the use of

ANN to classify moment-based feature input into one

of the class of viseme. ANN has been selected be-

cause it can solve complicated problems where the

description for the data is not easy to compute. The

other advantage of the use of ANN is its fault tol-

erance and high computation rate due to the mas-

sive parallelism of its structure (Kulkarni, 1994). The

functionality of the ANN to be less dependent on the

underlying distribution of the classes as opposed to

other classiﬁers such as Bayesian classiﬁer is yet an-

other advantage for using ANN in this application.

A supervised feed-forward multilayer percep-

tron (MLP) ANN classiﬁer with back propagation

learning algorithm is integrated in the visual speech

recognition system described in this paper. The

ANN is provided with number of training vectors

for each class during the training phase. MLP ANN

was selected due to its ability to work with complex

data compared with a single layer network. Due

to the multilayer construction, such a network can

be used to approximate any continuous functional

mapping (Bishop, 1995). The advantage of using

back propagation learning algorithm is that the inputs

are augmented with hidden context units to give

feedback to the hidden layer and extract features

of the data from the training events (Haung, 2001).

Trained ANNs have very fast classiﬁcation speed thus

making them an appropriate classiﬁer choice for real

time visual speech recognition applications.Figure 1

shows the block diagram of the proposed system.

3 METHODOLOGY

Experiments were conducted to evaluate the perfor-

mance of the proposed visual speech recognition ap-

proach. The experiments were approved by the Hu-

man Experiments Ethics Committee of the Univer-

sity. The experiment was designed to test the efﬁ-

ciency of different moments features in classifying 3

consonants when there was none or minimal shift be-

tween the camera and the mouth of the user between

the training and the testing data.

The ﬁrst step of the experiment was to record the

video data from a speaker uttering the three conso-

nants. The three consonants selected were a fricative

/v/, a nasal /m/ and a stop /g/. Each consonant was

repeated for 20 times while the mouth movement of

the speaker was recorded using an inexpensive web

camera. This was done towards having an inexpen-

sive speechless communication system using low res-

olution video recordings. The video camera focused

on the mouth region of the speaker and the camera

was kept stationary throughout the experiment with a

constant window size and view angle. A consistent

background and illumination was maintained in the

experiments. The video data was stored as true color

(.AVI) ﬁles and every AVI ﬁle had a duration of 2 sec-

onds to ensure that the speaker had sufﬁcient time to

utter each consonant. The frame rate of the AVI ﬁles

was 30 frames per second which is within the range of

standard frame rate for video cameras. One MHI was

generated from each AVI ﬁle. A total of 60 MHI were

produced for the 3 consonants, 20 for each consonant.

Example of the MHI for each of the consonants /v/,

/m/ and /g/ are shown in Figure 2.

SWT at level-1 using Haar wavelet was applied on

the MHI and the approximate image was used for

VISUAL SPEECH RECOGNITION USING WAVELET TRANSFORM AND MOMENT BASED FEATURES

343

Figure 2: The three consonants and the MHI for the conso-

nants.

analysis. The moment-based features were extracted

to characterize the different mouth movement of the

approximate image of MHI generated by the SWT. 49

moments -each of Zernike, geometric and ﬁrst six Hu

moments were computed. These features were tested

to determine the efﬁciency of the different moments

in representing the lip movement.

In the experiment, features from 10 MHI (for each

consonant) were used to train the ANN classiﬁer with

back propagation learning algorithm. The architec-

ture of the ANN consisted of two hidden layers and

the numbers of nodes for the two hidden layers were

optimized iteratively during the training of the ANN.

Sigmoid function was the threshold function and the

type of training algorithm for the ANN was gradient

descent and adaptive learning with momentum with a

learning rate of 0.05 to reduce chances of local min-

ima. The trained ANNs were tested by classifying

the remaining 10 MHI of each consonant that were

not used in the training of the ANN to test the perfor-

mance of the proposed approach. The performance

of these three moment-based features was evaluated

in this experiment by comparing the accuracy in the

classiﬁcation during testing.

4 RESULTS AND OBSERVATIONS

The experiment investigates the performance of the

different features in classifying the MHI of the 3 con-

sonants. The classiﬁcation results are tabulated in

Table 1. It is observed that the classiﬁcation accu-

racies of the three features (Zernike moments, geo-

metric moments and Hu moments) are very similar,

with Zernike moments and geometric moments yield-

ing marginally higher recognition rate (100%) com-

pared to Hu moment features. The results also in-

dicate a very high level of accuracy for the system

to identify the spoken consonant from the video data

when there is no relative shift between the camera and

the mouth.

Table 2 summarizes the recognition rates for the

three moment features. The results indicate that the

MHI based technique is able to recognize spoken con-

sonants with a high degree of accuracy.

5 DISCUSSION

The results indicate that the technique provides excel-

lent results for identifying the unspoken sound based

on video data, with error less than 5%. The results

using the three different image moments are all very

comparable. Hu moment has marginally higher er-

ror, but has signiﬁcantly smaller number of moments

used (only 6 moments) to represent the MHI com-

pared with Zernike moments and geometric moments,

which have 49. The higher order moments contain

more information content of the MHI (Teh and Chin,

1988).

While this error rate is far lower than the 90%

error reported in the review by (Potamianos et al.,

2003), the authors believe that it is not appropriate to

compare the work reported there to our work as this

system has only been tested for limited and selected

phones.

The promising results obtained in the experiment

indicate that this approach is suitable for classifying

consonants based on the mouth movement without re-

gard to the static shape of the mouth. The results also

demonstrate that a computationally inexpensive sys-

tem which can easily be developed on a DSP chip

can be used for such an application. At this stage,

it should be pointed that this system is not being de-

signed to provide the ﬂexibility of regular conversa-

tion language, but for a limited dictionary only, and

where the phones are not ﬂowing, but are discrete.

The current systems require the identiﬁcation of the

start and end of the phone, and the authors propose

the use of muscle activity sensors for this aim.

The authors would also like to point out that this

system is part of the overall system. This system is

designed for consonant type of sounds, where there is

facial movement during the phone. The authors have

also designed a separate system that is suitable for

vowels, and the two need to be merged together for

the complete system.

The authors believe that one reason for better re-

sults of this system compared with the other related

works is that it is not only based on lip movement, but

is based on the movement of the mouth. While lips

are important articulators of speech, other parts of the

mouth are also important, and this approach is closer

to the accepted speech models.

ICINCO 2006 - ROBOTICS AND AUTOMATION

344

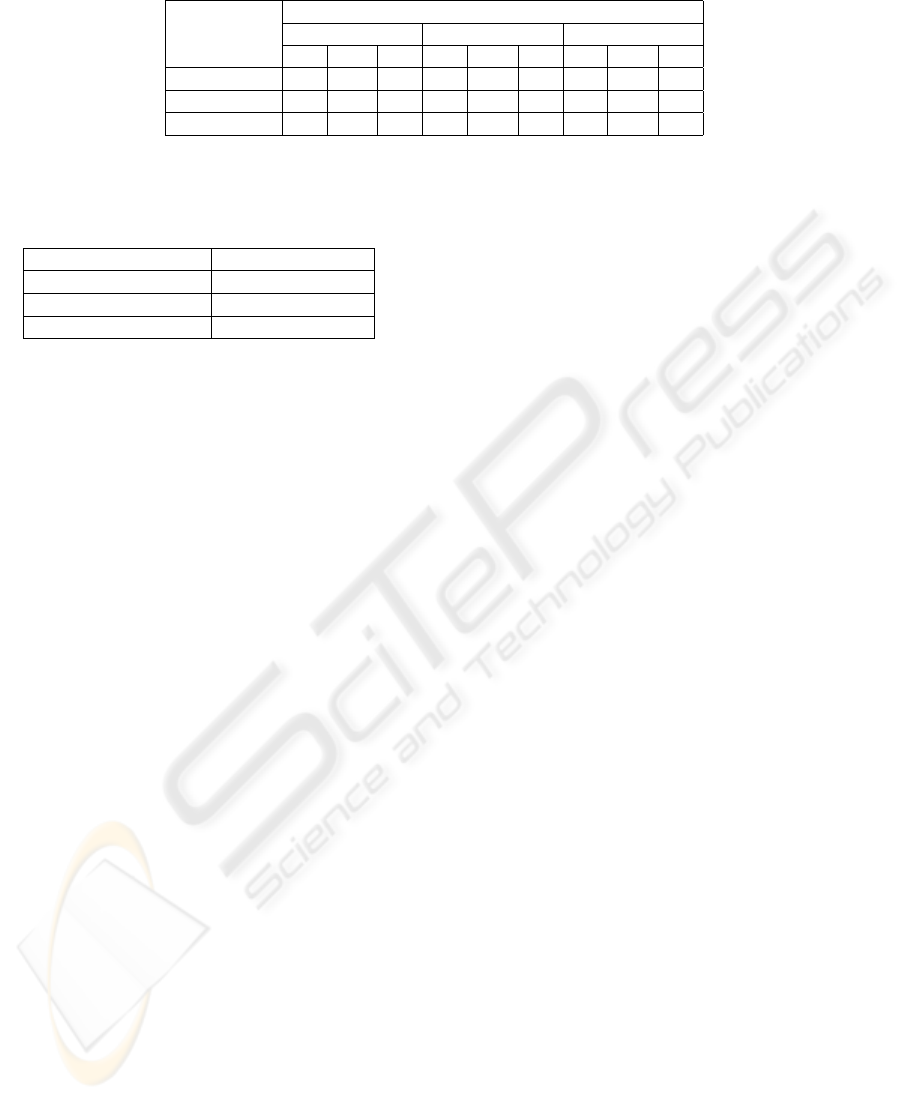
Table 1: Classiﬁcation results for different image moments extracted from the SWT approximate image of the MHI.

Predicted Consonants

Actual Zernike Geometric Hu

Consonants /v/ /m/ /g/ /v/ /m/ /g/ /v/ /m/ /g/

/v/ 10 - - 10 - - 10 - -

/m/ - 10 - - 10 - 1 9 -

/g/ - - 10 - - 10 - - 10

Table 2: Recognition rates for the different moment features

of the MHI.

Type of Moments Recognition Rate

Zernike Moments 100%

Geometric Moments 100%

Hu Moments 96.67%

6 CONCLUSION

This paper describes a visual speech recognition ap-

proach that is based on direct mouth motion represen-

tation and is suitable for real time implementation.

The low complexity of the proposed visual speech

recognition system is achieved by using image differ-

encing technique that represent the mouth motion of

the image sequence using grayscale images, motion

history image (MHI).

This paper focused on classifying English conso-

nants because pronunciation of consonants results in

more visually observable movement of the speech ar-

ticulators as compare to vowels. 2-D SWT and image

moments (Zernike moments, geometric moments and

Hu moments) are used to extract visual speech fea-

tures from the MHI and classiﬁcation of these features

is performed by ANN. The experimental results indi-

cate that such a system can produce high classiﬁca-

tion rate (approximately 100%) using moment based

features extracted from SWT approximate of MHI.

There is a need to identify the limitation of this

technique by testing the system on large number of

sounds, with the intent to determine the possible vo-

cabulary that maybe supported by such a technique.

Such a system could be used to drive computerized

machinery when in noisy environments. The system

may also be used for helping disabled people to use a

computer and for voice-less communication.

REFERENCES

Bishop, C. M. (1995). Neural Networks for Pattern Recog-

nition. Oxford University Press.

Bobick, A. F. and Davis, J. W. (2001). The recognition

of human movement using temporal templates. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 23:257–267.

Chen, T. (2001). Audiovisual speech processing. IEEE Sig-

nal Processing Magazine, 18:9–21.

Haung, K. Y. (2001). Neural network for robust recognition

of seismic patterns. In IIJCNN’01, Int Joint Confer-

ence on Neural Networks.

Hu, M. K. (1962). Visual pattern recognition by moment

invariants. IEEE Transactions on Information Theory,

8:179–187.

Khontazad, A. and Hong, Y. H. (1990). Rotation invariant

image recognition using features selected via a sys-

tematic method. Pattern Recognition, 23:1089–1101.

Kulkarni, A. D. (1994). Artiﬁcial Neural Network for Image

Understanding. Van Nostrand Reinhold.

Kumar, S. and Kumar, D. K. (2005). Visual hand

gesture classiﬁcation using wavelet transform and

moment based features. International Journal of

Wavelets, Multiresolution and Information Process-

ing(IJWMIP), 3(1):79–102.

Kumar, S., Kumar, D. K., Alemu, M., and Burry, M. (2004).

Emg based voice recognition. In Intelligent Sensors,

Sensor Networks and Information Processing Confer-

ence.

Liang, L., Liu, X., Zhao, Y., Pi, X., and Neﬁan, A. V.

(2002). Speaker independent audio-visual continuous

speech recognition. In IEEE Int. Conf. on Multimedia

and Expo.

Mallat, S. (1998). A Wavelet Tour of Signal Processing.

Academic Press.

Mukundan, R. and Ramakrishnan, K. R. (1998). Moment

Functions in Image Analysis : Theory and Applica-

tions. World Scientiﬁc.

Petajan, E. D. (1984). Automatic lip-reading to enhance

speech recognition. In GLOBECOM’84, IEEE Global

Telecommunication Conference.

Potamianos, G., Neti, C., Gravier, G., and Senior, A. W.

(2003). Recent advances in automatic recognition of

audio-visual speech. In Proc. of IEEE, volume 91.

Teague, M. R. (1980). Image analysis via the general theory

of moments. Journal of the Optical Society of Amer-

ica, 70:920–930.

Teh, C. H. and Chin, R. T. (1988). On image analysis by the

methods of moments. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 10:496–513.

VISUAL SPEECH RECOGNITION USING WAVELET TRANSFORM AND MOMENT BASED FEATURES

345