
A PATH PLANNING STRATEGY FOR OBSTACLE AVOIDANCE
Guillaume Blanc, Youcef Mezouar and Philippe Martinet
LASMEA
UBP Clermont II, CNRS - UMR6602
24 Avenue des Landais, 63177 Aubiere, France
Keywords:
Mobile robot, obstacle avoidance, path planning.
Abstract:
This paper presents an obstacle avoidance module dedicated to non-holonomic wheeled mobile robots.
Chained system theory and deformable virtual zone principle are coupled to design an original framework
based on path following formalism. The proposed strategy allows to correct the control output provided by
a navigation module to preserve the robot security while assuring the navigation task. First, local paths and
control inputs are derived from the interaction between virtual zones surrounding the robot and obstacles to ef-
ficiently prevent from collisions. The resulting control inputs and the ones provided by the navigation module
are then adequately merged to ensure the success of the navigation task. Experimental results using a cart-like
mobile robot equipped with a sonar sensors belt confirm the relevance of the approach.
1 INTRODUCTION
Whether a mobile robot uses an internal representa-
tion of its environment or not, the navigation strategy
that it applies can not ignored the risk to meet an un-
known obstacle on its way while performing a navi-
gation task. If such an event happens, the robot has
to react for the best. On one hand it must preserve its
security. On the other hand, it has to perform its main
task.
If the robot navigates according to a geometric map,
which models the free space as a subset of the config-
uration space, it is then possible to describe obstacles
by their configurations into the map. In this context,
a first approach to obstacle avoidance is to consider
it as a path planning problem under geometric con-
straints (Laumond, 1998). The second main approach
consists in confering on the robot a reflex behavior
without explicitly planning any geometric path or tra-
jectory. Typically, it can be done using the potential
field method (Khatib, 1986; Barraquand et al., 1992).
In this approach, the robot motions are under the in-
fluence of an artificial repulsive potential field push-
ing the robot away from the obstacles. This strategy
does not necessarily require geometric models of the
environment and of the obstacles since potential fields
can be defined directly from sensor data (sensor-based
reflex behavior). Generally, a sensor based approach
consits in mapping the robot control inputs with sen-
sor observations through a behavior model. The be-
havior model can be for instance inspired by neuro-
sciences as proposed in (Braitenberg, 1984; Filliat
et al., 1999) or would rather use sensor-based con-
trol formalism as proposed in (Samson et al., 1991).
This last formalism has been intensively exploited in
the context of mobile robotics. However, with such
a strategy, it can be difficult to manage the induced
kinematic constraints (nonholonomy) in presence of
obstacles. This issue is elegantly addressed by Zapata
et al through the DVZ (Deformable Virtual Zone) ap-
proach (Zapata et al., 1994). It consists in surrounding
the robot with a virtual zone which can be deformed
depending on two modes. The first one is called con-
trolled mode. The shape of the zone is modified ac-
cording to the internal state of the robot. The second
mode is the uncontrolled mode of deformation. The
shape of the zone is modified when an obstacle tries to
come into it. The control inputs are computed in order
to minimize the uncontrolled deformation. This pa-
per focuses on an obstacle avoidance module (OAM)
for a nonholonomic mobile robot. The environment
and the obstacles are not supposed explicitly mod-
eled. The navigation module is provided by an ex-
ternal algorithm as for instance the one proposed in
(Blanc et al., 2005). The OAM thus aims to assist the
navigation module by correcting the control inputs to
438
Blanc G., Mezouar Y. and Martinet P. (2006).
A PATH PLANNING STRATEGY FOR OBSTACLE AVOIDANCE.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 438-444
DOI: 10.5220/0001211604380444
Copyright
c
SciTePress

prevent potential collision with obstacles.
In a more general point of view, the OAM can be con-
sidered as a security filter acting on the control inputs
provided by an indepently designed navigation algo-
rithm. The OAM acts according to the local context
of obstacles and consequently, it can be classified as a
reflex obstacle avoidance strategy. As it is done with
the DVZ, a virtual observation zone surrounding the
robot is defined. The shape of this observation zone
varies with the instantaneous kinematic state of the
robot. The goal is to protect this zone from obsta-
cle intrusions. When an obstacle enters the observa-
tion zone, the shape of this zone is deformed to fit
the shape of the obstacle. This new shape is consid-
ered as a path that should be followed for avoidance.
The OAM provides a control vector which should be
applied to follow the planned path, and merges it ad-
equately with the one from the navigation module. In
an original way, the avoidance strategy consists thus
in a reflex action which is performed according to a
local path following based control.
2 MODELING
The OAM consists in acting on the control inputs
to thrust obstacles aside a zone which virtually sur-
rounds the robot. The main idea is to consider the
shape of entering obstacles as a path the robot has to
follow at a given distance which depends on the shape
of the virtual zone.
The proposed formalism is adequated to non-
holonomic mobile robots. It takes advantage of
the exact linearization of the mobile robot kine-
matic model through chained system (Samson, 1995).
Without loss of generality, our framework is illustrate
with a cart-like mobile robot.
2.1 Robot Model
The cart-like robot can be modeled as a unicycle
driven by a control vector composed of two kine-
matic inputs : U = [u
1
, u
2
]. An euclidian frame
F
R
, (O
R
, X
R
, Y
R
, Z
R
) is attached to the robot.
The origin O
R
is the unicycle control point and is
fixed on the wheels axle’s middle point of the cart-like
robot. u
1
and u
2
denotes respectively the longitudi-
nal and the rotational velocities of the unicycle. As
shown by Figure 1, X
R
carries u
1
whereas u
2
is ex-
pressed around Z
R
.
The robot is supposed to roll without slipping.
Whereas the avoidance strategy is based on a path fol-
lowing formalism, the robot kinematic model is ex-
pressed in a Frenet frame F
M
. Let M be the orthogo-
nal projection of O
R
on a curve ζ. We assume that the
distance from O
R
to ζ always remains smaller than
F
M
.
s
e
ρ
e
ϕ
u
1
u
2
O
R
F
R
Y
R
X
R
M
ζ
Figure 1: Robot kinematic model in a Frenet frame.
the minimal value of the curvature radius along ζ. In
this way, M is unique. F
M
is represented on Figure 1,
where s is the curvilinear abscissa associated to M on
ζ. e
ρ
and e
ϕ
are respectively the lateral and the angu-
lar deviations of the robot with respect to ζ. Let c(s)
be the curvature of ζ at M . The robot motions are
described with respect to F
M
by the following kine-
matics equations:
˙s =
u
1
cos e
ϕ
1 − e
ρ
c(s)
˙e
ρ
= u
1
sin e
ϕ
˙e
ϕ
= u
2
− ˙sc(s)
(1)
2.2 Observation Zone
Let us define a virtual zone, called observation zone
and surrounding the robot, as a planar curve ζ
z
lying
on Π , (O
R
, X
R
, Y
R
). The polar coordinates of
each point on Π will be denoted ρ for the module and
θ for the argument.
Let now f
z
be a continuous and derivable function:
f
z
:
[−π, π] 7→ IR
θ −→ ρ = f
z
(θ)
(2)
such that
∀θ ∈ [−π, π] , ρ > 0
f
z
clearly defines a virtual zone that surrounds O
R
in
Π. This virtual zone is a closed curve ζ
z
which marks
off a set Z with O
R
∈ Z
1
:
ζ
z
= inf {ρ > 0 | ρ = f
z
(θ)} (3)
1
given a set A, infA =
max {t ∈ [0 , +∞] | ∀a ∈ A , t < a}
A PATH PLANNING STRATEGY FOR OBSTACLE AVOIDANCE
439

ζ
o
ρ
θ
1c
u
2c
u
P
ζ
z
obstacle
ζ
f
ρ
θ
1c
u
2c
u
P
(a) (b)
Figure 2: Illustration of the definition of: (a) the observation
zone by ζ
z
, the obstacle shape by ζ
o
; (b) the free zone by
ζ
f
.
We assume now that an obstacle is known in F
R
as
a polar function f
o
in Π describing its shape. Let ζ
o
be the corresponding curve:
ζ
o
= inf {ρ > 0 | ρ = f
o
(θ)} (4)
ζ
o
defines the set O which contains the points lying on
the considered obstacle. If we assume that the robot
did not collide with the obstacle then O
R
6∈ O.
Figure 2(a) illustrates above definitions with an el-
liptic virtual zone and a single obstacle.
2.2.1 Uncontrolled Deformations
When an obstacle gets closer to the robot, it may
physically penetrate into the virtual zone. In this case,
Z ∩ O 6= ∅. We define the free set F as:
F = Z − O
Now consider the curve ζ
f
:
ζ
f
= min(ζ
z
, ζ
o
) (5)
ζ
f
is a closed curve, always defined since ζ
z
is also
a closed curve and F is the inner set defined by ζ
f
.
Note that ζ
f
can be considered as the result of the
deformation of ζ
z
by the uncontrolled intrusion of an
obstacle as illustrated by Figure 2(b).
2.2.2 Controlled Deformations
Till now, ζ
z
was only considered as a geometric curve
which did not depends on time since f
z
was fixed.
However, it may be judicious to adapt the shape of
ζ
z
with the navigation context. Remembering that the
robot is guided by a navigation module, ζ
z
may be
deformed in a controlled mode by taking into account
the input control vector U
c
= [u
1
c
, u
2
c
] provided by
this module. Then the definition of f
z
(refer to equa-
tion (2)) has to be modified: ρ = f
z
(θ, U
c
).
For instance, an appropriated deformation should be
to control a scale factor on ζ
z
according to u
1
c
, in
order to extend the observation zone when the robot
goes fast. If the robot goes slowly, it probably navi-
gates in a cluttered or unknown space. In this case, it
has to be reactive to obstacles and its motions should
not be too much constrained so that it can carry on
making progress.
If we now consider the robot as a volumic object in-
stead of a single point, it appears necessary to con-
strain the controlled deformations of ζ
z
with a low
limit. This low limit can be seen as a security zone
that includes the robot.
2.3 Security Zone
As the observation zone ζ
z
(refer to equation (3)), the
security zone is defined as a closed curve ζ
s
. The
associated function f
s
is designed in order that ζ
s
closely fits the area defined by the orthogonal projec-
tion of the robot volume on Π.
ζ
s
is not deformable. From a practical point of view,
it must be designed according to the minimal range
that embedded sensor are able to provide accurately.
No obstacle has normally to come within ζ
s
, but if un-
fortunately it happens, the obstacle must be detected
to adapt the control strategy. This also implies that ζ
s
should be within ζ
z
as illustrated in the Figure 3. The
controlled deformations of ζ
z
are thus limited:
∀θ ∈ [−π, π] , f
z
(θ, U
c
) ≥ f
s
(θ) (6)
Seeing its functional interest, ζ
s
plays an important
rule for the control design.
3 CONTROL DESIGN
3.1 Control Strategy
The avoidance control law aims to drive the robot in
order to get F = Z.
Let M be a point of ζ
f
defined as:
M , min {ζ
f
− ζ
z
} (7)
M is the orthogonal projection of O
R
on the piece
of curve ζ
f
which is not in ζ
z
. Note that if F = Z,
M = ∅. In this case, we consider that the coordinates
of M are not defined; otherwise, we note (ρ
M
, θ
M
, 0)
the coordinates of M in F
R
.
Now let us define the error e
ρ
which models the defor-
mation from ζ
z
to ζ
f
by the following signed distance
(see Figure 4):
e
ρ
= f
z
(θ
M
, U
c
) − ρ
M
(8)
ICINCO 2006 - ROBOTICS AND AUTOMATION
440
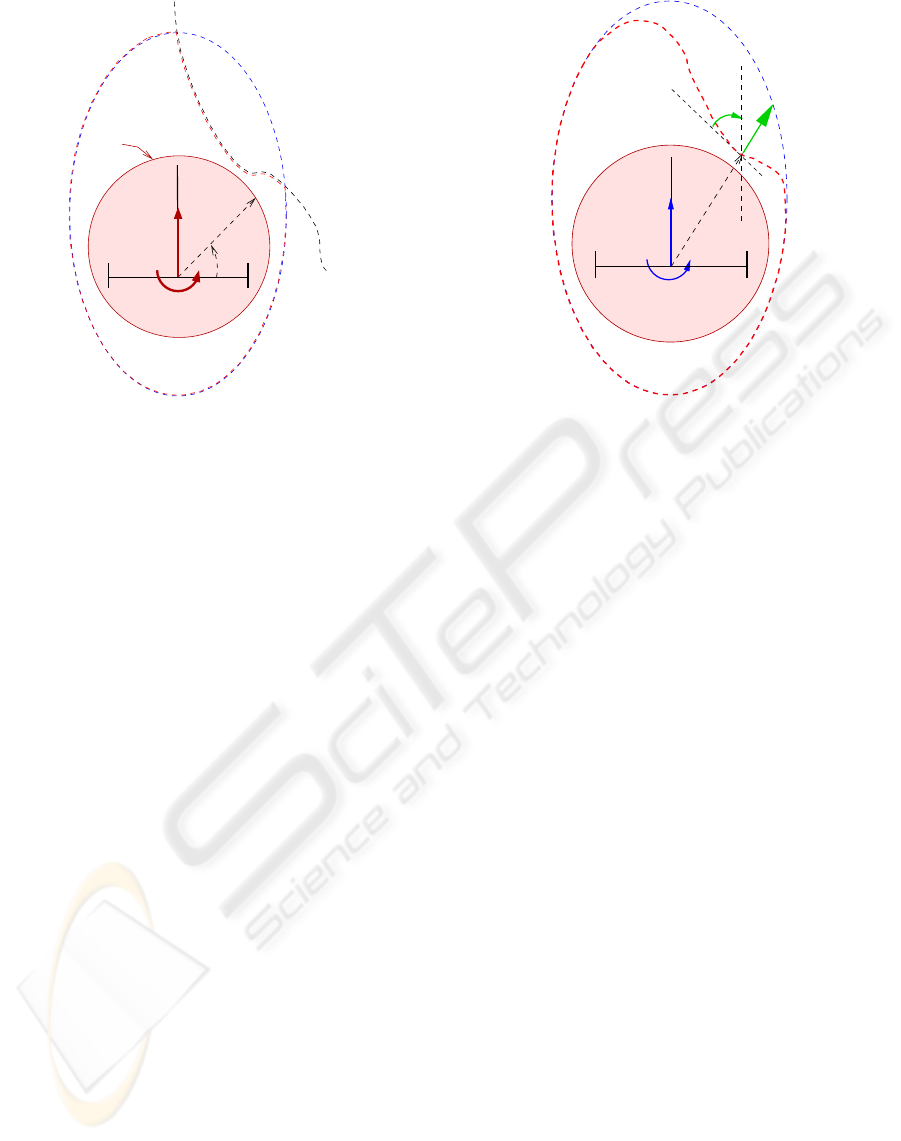
ρ
θ
1c
u
2c
u
P
ζ
s
Figure 3: The security zone ζ
s
.
e
ρ
is a lateral deviation which may be regulated to
zero to push away the obstacles from the virtual zone.
Let us also define the angular deviation e
ϕ
with re-
spect to the longitudinal axis X
R
as the orientation of
the tangent vector to ζ
f
at M . The avoidance con-
trol objective is to stabilize both e
ρ
and e
ϕ
to zero.
This defines a path following problem. In the sequel,
this issue is addressed using the theoretic framework
of chained systems (Samson, 1995).
3.2 Lateral Control
The state space model (1) can be converted into a
chained system of dimension three:
[a
1
, a
2
, a
3
] = [s, e
ρ
, (1 − e
ρ
c(s)) tan e
ϕ
] (9)
with a two dimensional control vector [m
1
, m
2
]
⊤
∈
IR
2
. The derivative of such a chained system with
respect to time is:
(
˙a
1
= m
1
˙a
2
= a
3
m
1
˙a
3
= m
2
(10)
If this state vector is derivated with respect to a
1
, then
it appears that resulting kinematic system is linear. A
simple control which asymptotically stabilizes a
2
and
a
3
thus consists on a proportional state feedback:
m
2
= −m
1
K
p
a
2
− | m
1
| K
d
a
3
, (K
p
, K
d
) ∈ IR
2
+∗
(11)
(K
p
, K
d
) determines the performances of the con-
troller and defines a settling distance for the regula-
tion of a
2
and a
3
to zero. These two gains control the
reactivity of the robot when avoiding an obstacle.
e
ϕ
e
ρ
u
1g
u
2g
M
ρ
M
R
Figure 4: Lateral control: Definition of errors to be regu-
lated for obstacle avoidance.
In equation (11), m
1
appears as a parameter which
does not influence the regulation dynamic. m
1
is di-
rectly linked to u
1
by:
m
1
= ˙s = u
1
cos(e
ϕ
) (12)
The system (10) leads to uncouple the controls m
1
and m
2
. This implies that u
1
and u
2
are also uncou-
pled. The rotational velocity resulting from the lat-
eral regulation of the robot with respect to the obsta-
cle will be denoted u
2
z
in the sequel. Independently
from u
2
z
, a longitudinal velocity u
1
z
can be used to
adapt the longitudinal velocity u
1
c
to the navigation
context.
3.3 Longitudinal Control
The value of the longitudinal velocity does not a
priori influence the lateral regulation performances.
Then, u
1
z
could take any value u
1
c
provided by the
navigation module without any dammage. From a
practical point of view, it is advantageous to reduce
it when the environment seems to become cluttered.
Firstly, this ensures that the robot can stop if an ob-
stacle is detected close to the frontier of the security
zone. Secondly, this allows to get more accurate and
stable data from sensors when obstacles come closer
to the robot. The strategy for longitudinal control
consists on applying an adaptative gain α on u
1
c
in
order to stop the robot if an obstacle is within de
security zone, and to get u
1
z
= u
1
c
if no obstacle is
observed within ̺
z
:
A PATH PLANNING STRATEGY FOR OBSTACLE AVOIDANCE
441

1c
u
ρ
θ
M
M
M
f
z
f
s
Figure 5: Longitudinal control.
α : [−π, π] 7→ [0, 1]
if M 6= ∅
α =
ρ
M
− f
s
(θ
M
)
f
z
(θ
M
) − f
s
(θ
M
)
if ρ
M
≥ f
s
(θ
M
)
α = 0 otherwise
otherwise
α = 1
(13)
and:
u
1
z
= α u
1
c
(14)
Of course, if the robot stops while a dynamic obsta-
cle intends deliberately to run into, the collision will
occur. At present, we do not focuses on this problem.
3.4 Global Control
As exposed in sections (3.2) and (3.3), the OAM pro-
vides a control vector U
z
= [u
1
z
, u
2
z
] which aims to
correct U
c
from a navigation module. u
1
z
is directly
linked to u
1
c
, however the computation of u
2
z
does
not take u
2
c
into account. The OAM must favor the
navigation module outputs if the local configuration
of obstacles allows it. One can confere more impor-
tance to U
z
when an obstacle draws near the security
zone. Let U
g
=
u
1
g
, u
1
g
be the result of the cor-
rection of U
c
by the OAM. U
g
is computed according
to the following equations:
u
1
g
= u
1
z
u
2
g
= γu
2
c
+ (1 − γ)u
2
z
(15)
If γ is taken equal to α, near the frontier of the secu-
rity zone, the importance given to u
2
z
would be max-
imum while u
1
z
tends to zero. In order to get a more
reactive behavior, the definition of f
z
is modified as
follow
∀θ ∈ [−π, π[ , f
z
(θ, U
c
) ≥ f
s
(θ) + ε (16)
where ε is a constant scalar which allows to keep a
zone around ζ
s
when u
1
z
is non-zero and the robot is
exclusively steered by u
2
z
:
γ : [−π, π] 7→ [0, 1]
if M 6= ∅
γ =
ρ
M
− f
s
(θ
M
) + ε
f
z
(θ
M
) − f
s
(θ
M
) + ε
if ρ
M
≥ f
s
(θ
M
) + ε
γ = 0 otherwise
otherwise
γ = 1
(17)
3.5 Singularities
The proposed control design conduces to some sin-
gularities which should not be ignored. They result
from the lateral control strategy. First, the point M
is not necessarily unique. Secondly, the curvature
c(s) is not defined if f
z
is not two times derivable
at θ
M
. Last, e
ϕ
may be equal to ±
π
2
. From a prac-
tical point of view, the first two singularities can be
shunned. Indeed, curves ζ
o
and ζ
f
result from inter-
polation of scanning range sensors data. They are not
usually treated as analytic curves but as a set of sam-
pled points corrupted by measurement noises. Conse-
quently, M is not chosen among many points. How-
ever, if a choice has to be made, criteria can direct
it. The closest point to the X
R
axis, which directs
the longitudinal robot motion, can be privileged. Fur-
thermore, since curves are sampled with a constant
step ∆θ , the k
th
derivative f
k
z
of f
z
are computed as
f
k
z
(θ) =
f
k−1
z
(θ+h)−f
k−1
z
(θ−h)
2h
, where h = n ∆θ and
n is a strictly positive integer. The curvature c(s) is
thus always defined.
The third singularity corresponds to the case where
the robot goes orthogonally to an obstacle. The state
(9) is no more defined and, as a consequence, not ei-
ther the control law (11). It is all the more problem-
atical that m
2
should exponentially increase since e
ϕ
tends to ±
π
2
. To avoid such a configuration, one can
impose m
2
= 0 when e
ϕ
tends to ±
π
2
. In this way,
the longitudinal control law prevents the robot from
colliding with the obstacle.
ICINCO 2006 - ROBOTICS AND AUTOMATION
442

4 IMPLEMENTATION
This section illustrates the proposed approach from a
practical point of view. The framework proposed in
sections (2) and (3) was applied to assist the driving
of an indoor mobile robot equipped with a telemetric
sensors belt.
The OAM has been implemented on an external stan-
dard PC which wireless controls a Pioneer robot. This
robot is equipped with a eight sonars belt. Telemetric
data are acquired at f
e
= 10Hz. The control inputs
are also cadenced at f
e
. Telemetric data are collected
as eight range values, associated respectively to each
sensor. None filtering is processed on these data and
none uncertainty on measures is taken into account.
4.1 Virtual Zones
The two virtual zones ̺
z
and ̺
s
are chosen as two
concentric circles. The diameter of the security zone
is set to φ
s
= 0.6m. In this way, ̺
s
surrounds every
sightless zone between two consecutive sensors. The
parameter ε is fixed to 0.3m. The diameter φ
z
of ̺
z
linearly depends on u
1
c
. It is a priori limited by the
maximum range of sensors (i.e 3m). However, the
maximum value of φ
z
is set to φ
zmax
= 1m in order
to not constrain the robot motion when the obstacles
are far away from ̺
z
. Let u
1
cmax
be the maximum
longitudinal velocity of the robot then φ
z
is given by:
φ
z
= (φ
s
+ 2ε)
1 −
u
1
c
u
1
c
max
+φ
z
max
u
1
c
u
1
c
max
4.2 Planning of a Straight Line
Although it is possible to interpolate the data at
each sample to obtain a smooth curve which roughly
delimits the set of obstacles observate by the sonars,
we refer the avoidance algorithm to a simple straight
line. This line determines ̺
o
. ̺
o
is defined by the
point M and a vector ∆
o
. M is obtained from the
observations at time k : σ
k
= [σ
1
k
, σ
2
k
, . . . , σ
8
k
]
as the closest point to O
R
within the circle ̺
z
. ∆
o
depends on the navigation module outputs.
Let Ω
c
=
u
2
c
f
e
be the instantaneous steering
angle which should have directed the robot if it was
only guided by the navigation module. The vector
Ω
c
z
R
, where z
R
is the unitary vector which directs
the axis Z
R
, represents the directing vector of the
instantaneous robot motion. Let σ
i
k
be the range
data holden to estimate the point M. Another range
data is needed to determine a second point N to
build ̺
o
. The choice falls on σ
i+1
k
if θ
M
≥ Ω
c
or
σ
i−1
k
otherwise. Then let θ
MN
be the argument of
the vector
−−→
MN . If θ
MN
> Ω
c
, then ∆
o
=
−−→
MN .
Otherwise, ∆
o
= Ω
c
z
R
. In this way, we take care
that the OAM does not servo the robot on a line from
which the navigation module would have a tendancy
to get the robot out of the way. If M is obtained from
σ
1
k
or σ
8
k
, N may not exist. Then ∆
o
is forced to
be Ω
c
z
R
.
In the case of a straight line following, we have
∀s, c (s) = 0 which implies a simplification of the
control design exposed in section (3.2). Equation (11)
leads to the following simple control law:
u
2
z
= −u
1
z
cos e
ϕ
3
K
p
e
ρ
− | u
1
z
cos e
ϕ
3
| K
d
tan e
ϕ
This law ruled the robot motion during the experi-
ments which results are presented in the next section.
4.3 Results
We have validated the OAM with two kind of experi-
ments.
The first one consists on a very simple robotic task. It
consists on going forward, with U
c
= [v, 0]
⊤
, where
v is a constant. We have tried for v a range of longitu-
dinal velocities from 0.1m.s
−1
to 0.5m.s
−1
, which is
a respectable value for an indoor robot. Initially, the
robot is placed in order to be directed to a wall, with
an incidence angle of approximately −
π
6
rad. The di-
ameter of the circular security zone is fixed to 0.6m
while ε is set to 0.3m. In these conditions, the OAM
works as it is forecast in such a simple case.
The second task is more interesting. The robot is tele-
operated in offices and corridors of our laboratory and
the operator can not directly see the robot. He only
can see the image provided by an embedded frontal
camera which has an angle of view of 60deg. Im-
ages are wireless transfered, what implies some un-
expected and non constant delays on the visual feed-
back. In this case the OAM ensures the robot secu-
rity and assists the operator. However, circular virtual
zones rapidely appear unadequated. When an obsta-
cle comes closer to the robot from a side, the OAM
tends to correct the trajectory and unexpected oscil-
lations of the robot trajectory are induced. Elliptic
zones should be a solution to this issue.
5 CONCLUSION
This paper has presented the design and an implemen-
tation of an obstacle avoidance module (OAM) which
aims to act on the robot control inputs in order to pre-
serve the security of the robot when it is driven by
a navigation module which does not take explicitely
into account the possible presence of unexpected ob-
stacles.
The OAM is based on an original obstacle avoidance
A PATH PLANNING STRATEGY FOR OBSTACLE AVOIDANCE
443

approach. It consists on assigning to the robot a reac-
tive behavior by following a dynamically computed
path which results from the local observation of the
robot environment. None a priori model of obsta-
cles is needed since their shape can be estimated from
range data when the robot get closer to them. This es-
timated shape serves as reference of a path following
based control law which aims to pushing away obsta-
cles from a virtual zone. This zone is a closed curve
surrounding the robot and its shape can be modified
according to control inputs provided by the naviga-
tion module.
The approach has been illustrated in a simple case.
However, we have put it on the test in much more
complex contexts. Helped by the OAM, a user can
teleoperate the robot from a different room to the one
where the robot is navigating. The user can safely
drive the robot when he has only a limited view of the
cluttered navigation environment from an embedded
camera looking forward.
Although a simple case of implementation, based on
circular virtual zones, has been presented, many dif-
ferent shapes for virtual zones have been tested. No-
tably, ellipses appears as a very judicious choice. The
efficiency of the OAM should be improved by using
sensors as a laser range scanner since it can provide
more numerous and accurate range data. The pro-
posed formalism should then be implemented without
resorting to restrictive practical simplifications.
REFERENCES
Barraquand, J., Langlois, B., and Latombe, J. (1992). Nu-
merical potential field techniques for robot path plan-
ning. IEEE Transactions on System, Man and Cyber-
netics, 22(2):224–241.
Blanc, G., Mezouar, Y., and Martinet, P. (2005). Indoor nav-
igation of a wheeled mobile robot along visual routes.
In IEEE International Conference on Robotics and
Automation, ICRA’05, Barcelona, Spain.
Braitenberg, V. (1984). Vehicles: Experiments in Synthetic
Psychology. The MIT Press, Cambridge, Massa-
chusetts.
Filliat, D., Kodjabachian, J., and Meyer, J.-A. (1999). Evo-
lution of neural controllers for locomotion and obsta-
cle avoidance in a 6-legged robot. Connection Sci-
ence, 11:223–240.
Khatib, O. (1986). Real time obstacle avoidance for ma-
nipulators and mobile robots. Int. Journal of Robotics
Research, 5(1):90–98.
Laumond, J. (1998). Robot motion planning and control,
volume 229, chapter Guidelines in nonholonomic mo-
tion planning, pages 1–54. Springer.
Samson, C. (1995). Control of chained systems. applica-
tion to path following and time-varying stabilization
of mobile robots. IEEE Transactions on Automatic
Control, 40(1):64–77.
Samson, C., Espiau, B., and Borgne, M. L. (1991). Robot
Control : The Task Function Approach. Oxford Uni-
versity Press.
Zapata, R., Lepinay, P., and Thompson, P. (1994). Reactive
behaviors of fast mobile robots. Journal of Robotic
Systems, pages 13–20.
ICINCO 2006 - ROBOTICS AND AUTOMATION
444
