AN OPTIMIZATION ALGORITHM TO IMPROVE SECURITY

OF ELECTRICAL ENERGY SYSTEMS

An hybrid approach based on Linear Programming and Load Flow Calculations

José V. Canto dos Santos, Arthur T. Gómez, Antônio G. Rodriguez

PIPCA – UNISINOS

P O Box 275, 93022-000 – São Leopoldo – RS, Brazil

Keywords: Security Analysis, Power System Restoration, Linear Programming.

Abstract: Power system restoration is one of the main problems in the electrical engineering area, due to the

improving dependency of electricity of the modern industrial society. The restoration of large electrical

power systems after the occurrence of serious blackouts is a complex problem where the basic goal is to

obtain the system configuration in order to supply loads with different priorities. The restoration is done

through stages and in each stage the service is restored to a predetermined set of loads. A method to solve

the basic problem in a real power system restoration process is presented in this work. The solution takes

into account the nonlinear electric network model (AC model) as well as its constraints and operational

limits. The fictitious network concept is extended to the reactive model. Linear programming, a new model

for the linearized power flow and conventional load flow calculation are also used. Results obtained with a

test system and with a large realistic system are presented.

1 INTRODUCTION

The occurrence of blackouts involving large sections

of electric energy systems is a real possibility,

however the remarkable investments for the

improvement of its security made by utilities. The

damages caused to industrial societies by these

blackouts are significant. With the continuous

growth of the complexity of the systems and the

demand for electric energy, it is necessary that the

treatment of systems after the occurrence of

blackouts become a part of operation procedures. In

this context, the power systems restoration (PSR)

has received special attention in the last years. It is

easy to see in the literature that the general solution

to the problem was still not found. The use of

Artificial Intelligence techniques to deal with the

restoration is widespread, with prominence for the

development of expert systems to support the

operators of systems. Some examples are the articles

of Kirschen and Volkman (1991) and Matsumoto et

al. (1992). In this approach, a basic point is the use

of the experience of operators about the electric

network in the construction of rules used in expert

systems, so it is natural that a certain degree of

dependence between the modelled electrical network

and the developed expert system is maintained.

Another approach to the problem is based on

optimization techniques, considered in a minor

number of works, whose distinguished examples are

Wu and Monticelli (1988) and of Huang et al.

(1995). According to Wu and Monticelli (1988) the

problem is non linear with restrictions,

combinatorial and multistage. The authors ponder

that if the restoration procedure will be determined

after the blackout, a basic restriction is the period in

which the system is without energy supply, so the

adopted model must allow the fastest solution to the

problem. There are other publications that focus

important details of the problem, like Adibi et al.

(1992).

In this work a method is presented regarding one

of the basic problems in restoration procedures: the

determination, in each stage of the process, of a

system configuration that accounts for the priority

load attendance. The method considers, in the static

point of view, the active and reactive aspects of the

systems and its main operative limits. The obtained

solutions can be used either for the determination of

restoration procedures during blackouts (on line use)

as well as in the planning of such procedures (off

line use). The presented method improves the PSR

processes; therefore it also improves the security of

operation of the electrical energy systems.

119

V. Canto dos Santos J., T. Gómez A. and G. Rodriguez A. (2006).

AN OPTIMIZATION ALGORITHM TO IMPROVE SECURITY OF ELECTRICAL ENERGY SYSTEMS - An hybrid approach based on Linear Programming

and Load Flow Calculations.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 119-123

DOI: 10.5220/0001212101190123

 SciTePress

2 PROBLEM FORMULATION

Restore a power system means to determine the best

form to guide the system from a state where its

integrity is harmed, after serious contingencies, to

another where priority loads are supplied and

operative limits are respected. This problem is

multistage, being the objective in each stage the

reestablishment of the service to a group of priority

loads. The main constraint is the time gap where

consumers are without energy. The restoration

process is complex, even in its static aspect, because

the high number of involved factors. In these factors

we can list the identification and scheduling of the

available resources of power generation, the

available equipment to be reconnected and the

operative limits of all the equipments installed in a

system.

In this work, the presented method starts in the

point where the electric system (or part of it) is in

blackout. Events that had carried the system for the

restorative state are not analyzed. In each stage of

the process, the priority loads and the equipment in

conditions to be used for the restoration are known.

2.1 Treatment of Disconnected

Systems

In the course of a blackout, the separation of the

system in diverse subsystems (islands) is frequent

due to loss of interconnections. To treat

disconnected systems in this work a fictitious

(dummy) network is used, in a procedure described

previously for electric transmission expansion

planning - Monticelli et al. (1982). In this procedure,

each out of operation branch of the system is

substituted by a fictitious branch with artificially

high impedance. The analyzed network is therefore

always connected (not having singulars matrices in

the solutions of type Ax = b) allowing the

verification of pathways with power flow need.

2.2 Alternative Model of Linearized

Power Flow (DCLF*)

In the PSR, an early problem is to determine which

generator (or generators) will be used to supply the

priority loads. The problem is more critical in the

beginning of the process, when diverse generators

may need to attend a few loads. To prevent a large

optimization problem (generation scheduling) in this

stage, a new model of linearized power flow was

developed. This model automatically determines the

generators near to loads and assigns the requested

power to each generator. As it will be seen ahead,

possible operation limits breakings are treated after.

The detailed electrical description of this model is

out of the scope of this work, but basically, the joint

use of the new model of linearized power flow with

fictitious network allow the work with disconnected

systems and also the verification of the power flows

in the fictitious branches. Thus, we can decide on the

necessity of the reconnection of an equipment, like it

will be seen forward.

3 PROPOSED APPROACH

The solution for each problem stage is obtained

through two main phases. The equipments that can

be returned to operation and loads to be restored are

defined in each stage. Each phase is described in a

summarized way below.

Phase I – DC Problem

It determines which branches have to be

reconnected to consider the active aspect of the

problem. This Phase is composed of 2 steps.

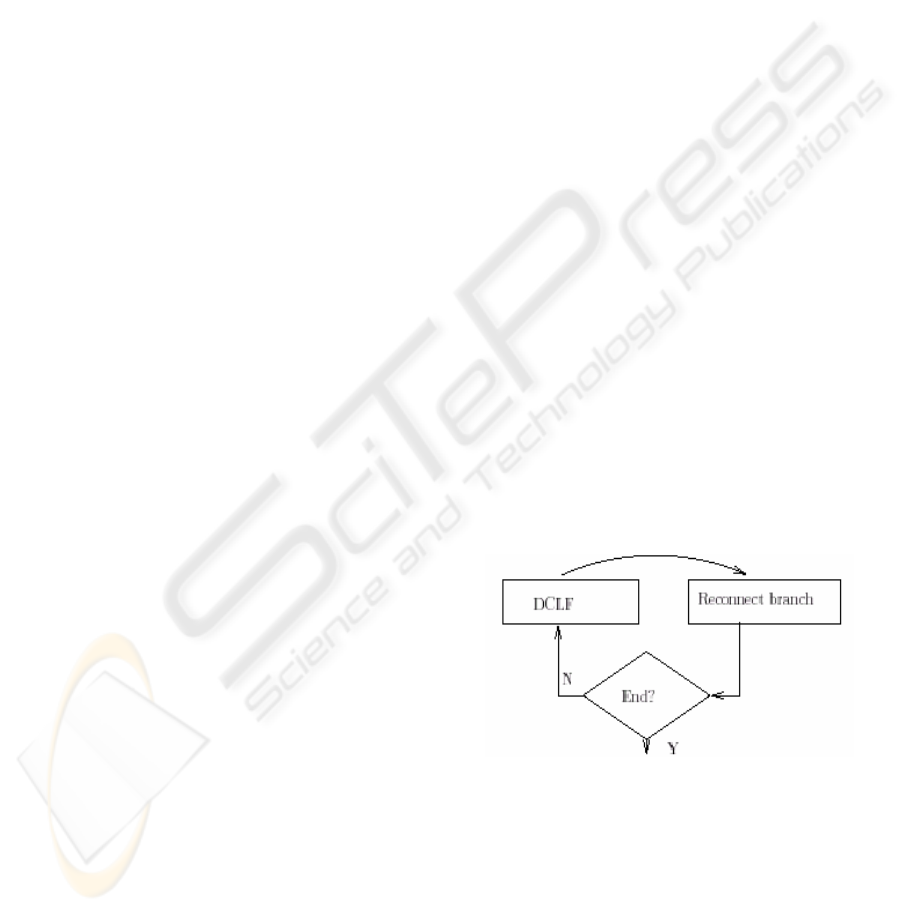
I.1. Determine branches to be reconnected using the

fictitious network and the alternative model of

power flow described in the previous section. A

DCLF* is performed after and the more loaded

fictitious branch is reconnected (when a branch is

reconnected the fictitious parameters are substituted

by the real ones) until there is no more considerable

flow in the fictitious network - see Figure 1.

Figure 1: Simplified vision of the step I.1.

I.2. If there are limit violations in the injections of

the generators or in the branches flows after the I.1

step is finished, a Linear Programming model

(LPM) is performed and, if necessary, new branches

are reconnected. The load cut is not allowed in this

phase, aiming at the integral supply of priority loads,

so the LPM calculation may not be possible. In this

case, the most loaded branch in the last solution of

DCLF* is successively relocated and a new LPM is

executed. When the LPM presents a solution, the

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

120

(1)

(2)

(3)

(4)

(5)

linearized power flow model is the conventional.

The LPM determines how much active power is

needed from each generator assuring that their limits

will be respected. Aiming at maintain the solution

next to the obtained in the I.1 step, the LPM model

looks for a solution where the limits are respected

with a minimum deviation from the current point.

The problem is described as follows.

III

PCPCMin Δ

′

+Δ

′

subject to:

=Δ−Δ

∑∑

0max

.0 PPP

−≤Δ≤

.0 PP

≤Δ≤

0max0min

kmkmkmkmkm

PPPPP −≤Δ≤−

where: nb - number of buses of the system, C - costs,

, and

- increments of increase and reduction

in the injections P

. P

e P

max

.- initial active powers

and maximum limits for injections.

P ,

min

P ,

max

P and

PΔ - flows of active power in

the initial solution, limits and increments for flows.

In the end of this phase we have a composed

network with branches, generators and loads with all

its limits respected.

Phase II - AC Problem

In this stage the network obtained in Phase I is

tested and, if necessary, modified to comprise the

reactive part of the system. Equipment that is not

reconnected is still represented for fictitious

parameters. This phase is executed in three steps, as

seen below.

II.1. A reactive dispatch for the network is

performed having as objective function the use of

reactive sources associated costs. In this dispatch,

the limits for voltage are relaxed in buses not

reconnected that possess non static sources of

reactive power, allowing the algorithm to allocate

reactive power if necessary. The limits for reactive

injections in priority buses are such that the

attendance of these injections is guaranteed. CRIC

Model (Carpentier, 1986) is used in sensitivity

between reactive power and magnitudes of voltage,

providing that the reactive power and the active

problem are managed in a nearly independent form.

II.2 The reconnection necessity of reactive

sources in the network buses configured in Phase I is

verified after step II.1. Later, it is verified if the

constructed network is in operation condition. This

is made using a non linear power flow calculation

with data collected in previous stages. If the solution

is available, end of the stage and beginning of the

next one solution. In contrary, phase II.3 must be

carried through.

II.3 It is verified in this stage the need of reactive

sources situated in buses that had not been

reconnected in Phase I. The bus is incorporated in

the system during this process by the reconnection

of the branches with bigger reactive flow until a bus

already ‘energized’ is reached. The power flow for

the new configured network is then calculated. If

this calculation has solution, end of the stage and

beginning of the next one. In contrary, stage II.1

must be carried through again, with new data.

4 TESTS

Dual Linear Programming and software MINOS was

used in the implementation. The fast decoupled load

flow (Monticelli et al., 1990), version BX, was used

for the non linear case.

4.1 IEEE-14 Test System

The IEEE-14 test system (Freris and Sasson, 1968)

is small, hence is adequate for the obtained results

description. For this system, it was considered an

occurrence of a general blackout and that the

generators of buses 1 and 2 and all the 20 branches

were available for the restoration of the net. Two

stages had been defined, first with priority loads in

the buses 4 and 12, and the second with the supply

of all system load objective.

In the first stage solution was obtained a network

with 5 buses and 4 branches. After, the network was

expanded for 13 buses and 15 branches in the second

stage. In both stages, the objective of supply priority

loads respecting the existing limits was reached. In

first stage solution, stages I.2 and II.3 have not been

needed. This fact has been observed in diverse tests

with different systems. Solution details are supplied

in Tables 1 and 2 and configured network topology

is shown in Figure 2.

AN OPTIMIZATION ALGORITHM TO IMPROVE SECURITY OF ELECTRICAL ENERGY SYSTEMS - An Hybrid

Approach Based on Linear Programming and Load Flow Calculations

121

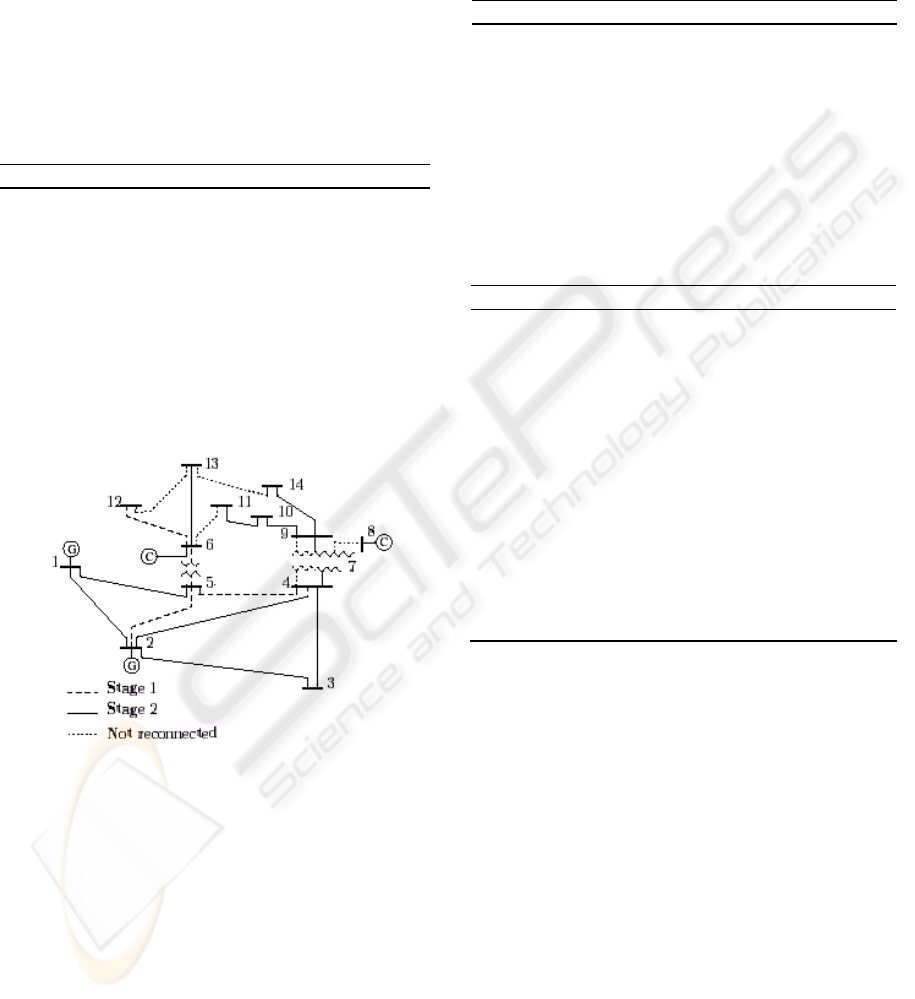
Table 1: Tests with IEEE-14 test system.

Table 2: Tests with IEEE-14 test system.

Figure 2: Solution for IEEE-14 test system.

4.2 Large Realistic System

In this test we used a large realistic system

configuration with 810 buses and 1340 branches.

The test presented here considers the occurrence of a

system blackout and that all its components were

available to be reconnected for operation. Two

stages of restoration has been proceeded. In the first

stage the objective was to supply only two important

loads totalizing 1027 MW. In second and the last

stage the objective was the supply of all the system

loads, of about 40000 MW. In the first stage

solution, the system configuration consisted of 2

sub-nets (assigned as A and B) in independent

operation and it was obtained without necessity of

steps I.2 and II.3. Tables 3 - 4 show the solution for

this test.

Table 3: Tests with a large realistic system.

First stage solution

Number of reconnected buses -

step I.1

Number of reconnected branches

- step I.1

Reconnected equipments– Phase

Load flow calculations – Phase II

Generators in activity 4

Table 4: Tests with a large realistic system.

Second stage solution

Number of reconnected buses - step I.1

747

Number of reconnected branches - step

I.1

1198

Number of reconnected buses - step I.2

Number of reconnected branches - step

I.2

Equipments reconnected – Phase II 6

Load flow calculations – Phase II

Generators in activity

Number of reconnected buses 760

Number of reconnected branches 1223

5 CONCLUSION

In this work a method was presented to assist

processes of power systems restoration, solving one

of the basic problems in such procedures: the

determination of the system configuration adjusted

for the priority load supply in each stage of the

process. Beyond linear programming, the method

uses a new model of linearized power flow and an

expansion of the fictitious net concept. These two

developments can be applied in other areas of

electric energy systems analysis. The developed

approach, simple but robust, is an analytical method

that can be applied to any electric system whose

restoration after a blackout is necessary. Also, it

allows for an easy modeling of typical circumstances

of a system in the restorative state. In the performed

simulations the obtained results had been fully

First stage solution

Reconnected buses - step I.1 2 4 5 6 12

Reconnected branches - step I.1 2-5, 4-5, 5-6, 6-

Reconnected equipments – Phase

Load flow calculations – Phase II 1

Second stage solution

Reconnected buses - step I.1 3 7 9 10 11

13 14

Reconnected branches - step I.1 3-4, 4-7, 7-9,

6-13, 9-10, 9-14,

10-11

Reconnected buses - step I.2 1

Reconnected branches - step I.2 1-2, 2-3, 1-5, 2-4

Equipments reconnected – Phase II -

Load flow calculations – Phase II

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

122

satisfactory and the necessary computational

efficiency for execution in real time was reached.

Results revealed that, in each stage of the restoration

process, depending on the definition of the set

priority loads, the necessary equipment number for

system recompose the can be smaller than the

system total. This fact was expected since most often

the systems operate with a safety margin.

Research in progress points to the necessity of

inclusion in the developed methodology of other

problem aspects still not focused, like an application

of combinatorial optimization procedures.

REFERENCES

Adibi, M. et al. (1992). Special Considerations in Power

System Restoration. IEEE Transactions on PWRS,

EUA, 7(4): 1419-1427.

Carpentier, J. (1986). CRIC, a New Active Reactive

Decupling Process in Load Flows, Optimal Power

Flow and System Control. Proceedings IFAC

Conference on Power Systems and Power Plan

Control, China, p.65-70.

Freris, L., Sasson, A. (1968). Investigation of the Load

Flow Problem. Proceedings of IEE, Inglaterra,

115(10):1459-1470.

Huang, J. et al. (1995). A Systematic Method for Power

System Restoration Planning. IEEE Transactions on

PWRS, EUA, 10(2): 869-875.

Kirschen, D., Volkman, T. (1991). Guiding a Power

System Restoration With an Expert System, IEEE

Transactions on PWRS, EUA, 6(2): 558-566.

Matsumoto, K. et al. (1992). Knowledge-Based Systems

as Operational Aids in Power Systems Restoration.

Proceedings of the IEEE, EUA, 80(5): 689-697.

Monticelli, A. et al. (1982). Interactive Transmission

Network Planning Using a Least-Effort Criterion.

IEEE Transactions on PAS, EUA, 101(10): 3919-

3925.

Monticelli, A. et al. (1990). Fast Decupled Load Flow:

Hypothesis, Derivations and Testing. IEEE

Transactions on PWRS, EUA, 5(4):1425-1431.

Wu, F., Monticelli, A. (1988). Analytical Tools for Power

System Restoration - Conceptual Design. IEEE

Transactions.

AN OPTIMIZATION ALGORITHM TO IMPROVE SECURITY OF ELECTRICAL ENERGY SYSTEMS - An Hybrid

Approach Based on Linear Programming and Load Flow Calculations

123