TOWARDS A SLAM SOLUTION FOR A ROBOTIC AIRSHIP

Cesar Castro, Samuel Bueno

Computer Vision and Robotics Division, CenPRA

Rod. SP 65, km 143.6, 13069-901, Campinas-SP, Brazil

Alessandro Victorino

INRIA-Sophia Antipolis, ICARE project

2004, Route des Lucioles, 06902, Sophia Antipolis , France

Keywords:

SLAM, localization, mapping, Kalman ﬁltering, UAVs.

Abstract:

This article presents the authors ongoing work towards a six degrees of freedom simultaneous localization and

mapping (SLAM) solution for the Project AURORA autonomous robotic airship. While the vehicle’s mission

is being executed in an unknown environment, where neither predeﬁned maps nor satellite help are available,

the airship has to use nothing but its own onboard sensors to capture information from its surroundings and

from itself, locating itself and building a map of the environment it navigates. To achieve this goal, the airship

sensorial input is provided by an inertial measurement unit (IMU), whereas a single onboard camera detects

features of interest in the environment, such as landmark information. The data from both sensors are then

fused using an architecture based on an extended Kalman ﬁlter, which acts as an estimator of the robot pose

and the map. The proposed methodology is validated in a simulation environment, composed of virtual sensors

and the aerial platform simulator of the AURORA project based on a realistic dynamic model. The results are

hereby reported.

1 INTRODUCTION

Beside their use as military surveillance platforms,

Unmanned Aerial Vehicles (UAVs) have a wide spec-

trum of potential civilian observation and data acqui-

sition applications. Usually, unmanned aerial plat-

forms are airplanes, helicopters or, more recently, air-

ships - also known as lighter-than-air (LTA) vehicles.

Unmanned airships have extended airborne capa-

bilities and large payload to weight ratio. They are

therefore best suited for low altitude, low speed or

hovering airborne data gathering missions, where the

vehicle should also take-off and land vertically (Elfes

et al., 1998). In this context, Project AURORA –

Autonomous Unmanned Remote mOnitoring Robotic

Airship – was proposed, aiming the gradual estab-

lishment of the technologies required for autonomous

operation of unmanned robotic airships (Elfes et al.,

1998; Bueno et al., 2002). Presently, AURORA LTA

robotic platform consists of (de Paiva et al., 2006):

i) a 10.5 m long, 34 m

of volume and 10 Kg pay-

load capacity nonrigid airship; ii) an onboard sys-

tem containing a PC/104 CPU with RT Linux, sen-

sors and actuators; iii) a portable PC with RT Linux

ground station for system operation; iv) a communi-

cation system comprising radio modems, analogical

and short range wireless Ethernet video links. The

onboard sensor package mainly includes: a GPS, an

Inertial Measurement Unit (IMU), a single ﬁrewire

IEEE 1394 digital camera and a Wind sensor. Exper-

imental results achieved so far include path following

ﬂight through a set of pre-deﬁned way points under

lateral and longitudinal control; experimental valida-

tion of visual servoing line following strategies are

under way.

Other important research efforts on robotic air-

ships are described in (Kantor et al., 2001; Wimmer

et al., 2002; Hygounenc et al., 2004) and, consider-

ing Planetary Exploration missions, in (Elfes et al.,

2003). Unmanned LTA vehicles are also suited for

stratospheric HALE (High Altitude Long Endurance)

operation, and efforts in this sense have been carried

out in Japan, Korea, Europe and USA, involving in-

dustry and academia.

For UAVs in general, and for AURORA in particu-

lar, an important aspect of the aircraft embedded sys-

tem is to determine the aerial platform position and

orientation in space. To do so, the most common ap-

proach is to use an inertial navigation system (INS) or

external navigational aids (such as a GPS). However,

241

Castro C., Bueno S. and Victorino A. (2006).

TOWARDS A SLAM SOLUTION FOR A ROBOTIC AIRSHIP.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 241-248

DOI: 10.5220/0001213202410248

 SciTePress

Figure 1: The AURORA project robotic aerial platform.

inertial systems diverge over time and GPS informa-

tion might not always be available. Besides, neither

inertial navigation nor satellite systems provide infor-

mation about the surroundings of the airship, which

means localization with respect to the environment is

not possible. So, more important than ﬁnding the pose

of the vehicle is to do so autonomously, using nothing

but its embedded sensors, with no external sensors, no

predeﬁned maps or satellite help. Furthermore, local-

ization in an unknown environment implies not only

pose determination but also incremental map build-

ing. The process in which a mobile robot constructs

a map and, while doing it, locates itself in it, is called

Simultaneous Localization And Mapping (SLAM).

Robotic mapping started with approaches based on

occupancy grids (Elfes, 1987; Elfes, 1989), but it

was only with the work of Smith, Self and Cheese-

man (Smith et al., 1987; Smith et al., 1988) simul-

taneous localization and mapping was ﬁrst formu-

lated as a probabilistic estimation problem. Since

then, interest in SLAM increased and several tech-

niques were developed, taking the extended Kalman

ﬁlter (EKF) approach further (Castellanos et al., 1999;

Castellanos et al., 2001). From the indoors robotics

research community, these solutions were then taken

to open spaces, where the size of the environment

and of the map became a concern (Sukkarieh et al.,

1999; Guivant and Nebot, 2001; Bailey, 2002; Guiv-

ant and Nebot, 2003). Finally, it reached aerial ro-

bots. Some interesting solutions to the SLAM prob-

lem have been posed at the international aerial robot-

ics community, consisting of directly correcting the

IMU readings with the aid of a GPS (Panzieri et al.,

2002) and/or updating the prediction by integrating

the inertial navigation data with observations of the

environment (made by an exteroceptive sensor such as

a range ﬁnder or a camera). The aerial SLAM prob-

lem has received relevant attention from the robotic

community over the last years (Ruiz et al., 2001; Kim,

2004; Langelaan and Rock, 2005; Wu et al., 2005)

but, even though many advances and partial solutions

have been proposed, it remains an open problem when

related to autonomous aerial navigation in unknown

and unstructured environments.

Considering the present status of Project AU-

RORA, in this article we present a ﬁrst effort towards

the establishment of a 3D SLAM solution, with six

degrees of freedom (DoF), speciﬁcally aiming to en-

hance the autonomous capability of the robotic air-

ship. An IMU is used in an inertial navigation model

to calculate the displacement of the airship during a

time interval, while a vision system, in which a single

onboard camera is used to capture landmark informa-

tion from the environment, allows the computation of

the map and of the airship pose with respect to it. An

EKF is used to fuse all the information and calculate

the uncertainty of the estimation.

After this introductory section, the remaining parts

of this article are organized as follows. Section 2

describes the methodology used to achieve SLAM

through an extended Kalman ﬁlter. Section 3 shows

the simulation results of the methodology. Finally,

Section 4 stresses the concluding remarks and the

future work concerning the implementation of such

methodology on the real airship and its evolution.

2 SYSTEM DESCRIPTION

In this section, the mathematical formulation of the

problem is derived. The Kalman ﬁltering approach to

sensor fusion and autonomous localization and map-

ping is presented, along with the equations that de-

ﬁne the airship movement and the observation model,

which will lead to feature matching and state augmen-

tation.

2.1 SLAM Architecture

Suppose that the airship is placed in an unknown lo-

cation, with no prior information about its surround-

ings. It is equipped with an IMU, which provides roll,

pitch and yaw velocities as well as linear accelera-

tions in the body reference frame, and a single cam-

era, which can be used to take relative measurements

between features in the environment (their absolute

locations are not known) and the camera itself. Usu-

ally, the IMU readings are fed to the inertial naviga-

tion system (INS) of the airship that computes the rel-

ative displacement of the vehicle in a geodesic refer-

ence frame. In the present work, as the vehicle moves

around, features are observed by the camera and fused

to the IMU data in order to build a map and minimize

localization errors of both vehicle and map features.

ICINCO 2006 - ROBOTICS AND AUTOMATION

242

The INS equations are inserted in the vehicle kine-

matic model.

An extended Kalman ﬁlter (EKF) is used as a state

estimator for both the vehicle location and the map,

propagating ﬁrst-order uncertainty, in an approach

known as Stochastic Mapping(Smith et al., 1987;

Smith et al., 1988). For a map with N features, the

system state vector

x is deﬁned as the estimate of the

vehicle state vector

augmented with the map state

vector

, so that

x =













. (1)

The state vector is accompanied by a covariance

matrix P, which represents the uncertainty in the state

vector, deﬁned as

P =







v,v

v,m1

. . . P

v,mN

m1,v

m1,m1

. . . P

m1,mN

mN,v

mN,m1

. . . P

mN,mN







(2)

In the following sections, the kinematic model of

the airship using the IMU inputs is derived, along with

the observation model. In the estimation process, the

kinematic model is used to predict the airship pose

and estimate the increase in the pose uncertainty. The

observation model is used to update the previous pre-

diction and reduce the uncertainty of the estimation

based in the observations.

2.2 Kinematic Model

The vehicle state vector is deﬁned as

(3)

where vectors

p and

v are, respectively, the position

and the velocity of the airship in earth reference. The

orientation of the robot is represented by the quater-

nion vector

q. Although it’s a non-mimimal represen-

tation of orientation, a quaternion is used in order to

avoid linearization problems and singularities of other

representations.

The prediction of the robot state

x(k|k − 1) is ob-

tained from its last pose and the signals provided by

the IMU that constitute the input u(k) of the inertial

navigation model, composed of: f , the linear accel-

eration, and ω, the angular velocity, both in frame of

reference ﬁxed in the airship:

(k|k − 1) = f(

(k), u(k), w

(k))

p(k − 1)

v(k − 1)

q(k − 1)

∆p

∆v

∆q

(k)

, (4)

where w(k) represents uncorrelated, zero-mean

process noise errors with covariance Q(k) and

∆p

∆v

∆q





v(k − 1)t + C

f t

(

D ω + ε q(k − 1)) t





, (5)

D =







−q







, (6)

ε = 1 − kq(k − 1)k

. (7)

It is important to notice that C

is the direction co-

sine matrix obtained from

q(k − 1), which takes from

the airship reference frame (B) orientation to the earth

reference frame (W ) orientation, D is also computed

from

q(k − 1), and ε represents an integration correc-

tion gain, which comes into place if the norm of the

quaternion is different than one.

2.3 Observation Model

It is important to investigate how the observations of

the landmarks relate to its actual position. In this

work, it is considered that the visual sensor returns to

the system the relative position between camera and

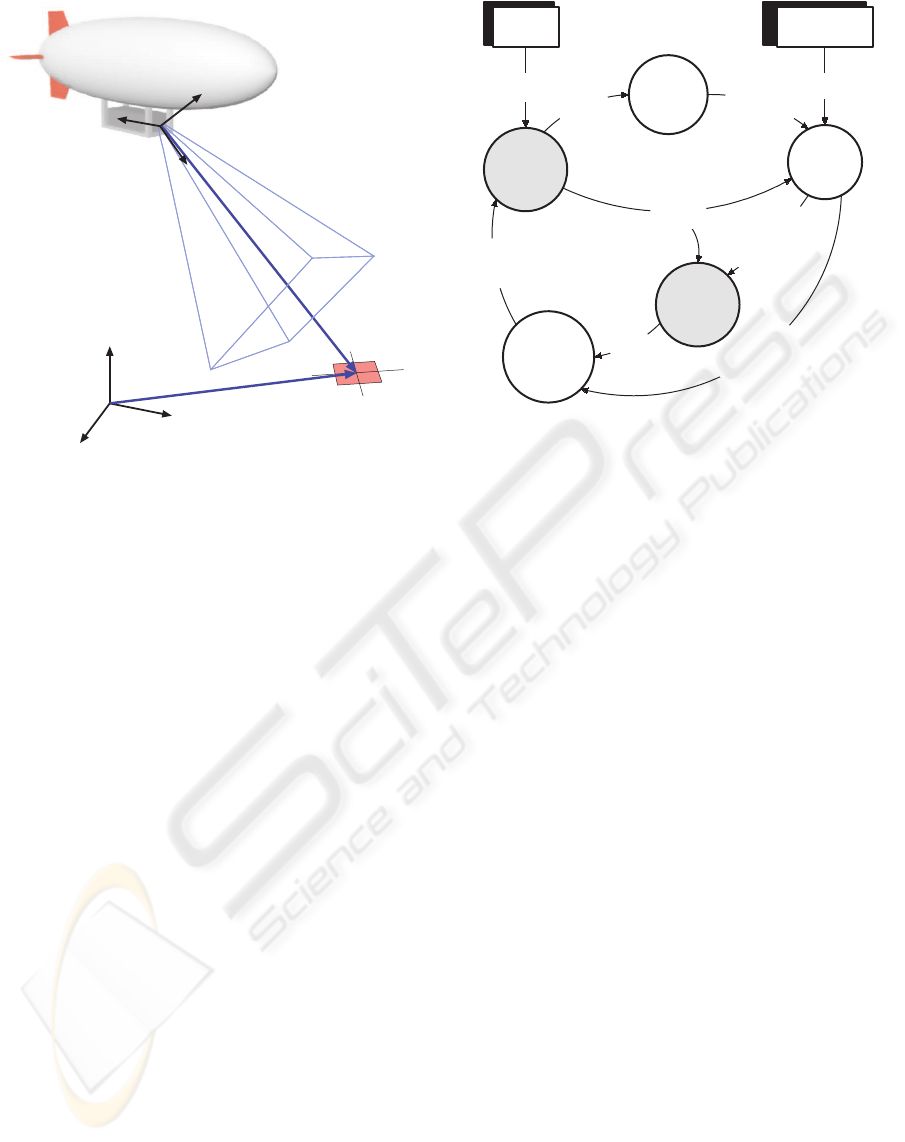
landmark, as shown in ﬁgure 2.

Each map feature is represented by its cartesian

threedimensional coordinates in the earth-ﬁxed frame

W , while the observations consist of the cartesian

threedimensional coordinates of the features in the

camera-ﬁxed frame C. Considering the camera frame

to be a known rotation of the airship body frame B, it

is possible to specify each a map feature as

= g(x

, z

)

= p(k) + R

)), (8)

where R

(·) is a function that uses a quaternion to

rotate from the camera orientation to the body ori-

entation (the airship orientation) and R

(·) rotates

a vector from the body frame to the world frame.

Taking the inverse of the previous equation, the ob-

servations at any instant can be predicted from the

state vector with the resulting observation model:

= h(x

, x

) + v

(k)

= g

−1

, x

) + v

(k)

= R

− p)) + v

(k), (9)

TOWARDS A SLAM SOLUTION FOR A ROBOTIC AIRSHIP

243

Figure 2: The airship observing a landmark.

with the rotation functions following the same nota-

tion already speciﬁed and v

(k) being uncorrelated,

zero mean observation noise with covariance R(k).

2.4 Estimation Process

The general state estimation process using the ex-

tended Kalman ﬁlter is represented in Fig. 3. At the

kth step, the kinematic model of the robot is used,

along with the inputs from the IMU, to compute a

prediction

x(k|k − 1) and the covariance P(k|k − 1).

Because the IMU readings do not contain any map in-

formation, the uncertainty in the inputs is reﬂected in

the vehicle state uncertainty, which should increase.

An observation prediction h(

x(k|k − 1)) is then cal-

culated and compared to the real observation z(k),

obtained from the vision system. From that compar-

ison, the observations are divided into matched and

unmatched observations. The ﬁrst are used to gener-

ate the estimate

x(k|k) and P(k|k) (the uncertainty

should decrease, since the pose with respect to the

map can be corrected), while the second are used to

augment the state vector and the associated covari-

ance matrix with new map entrances.

2.4.1 Prediction

The prediction of the state vector is obtained directly

from (4), derived in section 2.2. Because the map is

considered static with respect to the earth frame, the

map transition equation is

(k|k − 1) =

(k − 1), (10)

Vision System

(EKF )

predict

(EKF )

update

predict

obs

augment

match

obs

matched

observations

unmatched

observations

(

)

Pa(

)

(

)

(

)

-1)

h(x(

-1))

-1)

)

IMU

Figure 3: Structure of the SLAM system.

which leads to the full state transition equation:



(k|k − 1)





(k − 1), u(k), 0)

(k − 1)



(11)

However, as it was already mentioned, the predic-

tion implies an increase of the airship pose uncer-

tainty, since the IMU readings contain errors. There-

fore, the covariance matrix must be recalculated to re-

ﬂect that change. This is done through the following

equation:

P(k|k − 1) = ∇f

P(k − 1) ∇f

+∇f

Q(k) ∇f

, (12)

in which ∇f

and ∇f

are the jacobians of f with

respect to the state vector and the input, respectively.

The diagonal matrix Q(k) represents a model of the

error covariance in the sensor readings.

2.4.2 Update

In order to update the prediction x(k|k − 1), using the

landmarks perceived by the vision system, the equa-

tions derived in section 2.3 are used. From (9), it is

possible to calculate the uncertainty in the observa-

tion prediction at instant k, S(k), which is related to

the system state and the observation errors:

S(k) = ∇h

(k)P(k|k − 1)∇h

(k) + R(k), (13)

where ∇h

(k) is the Jacobian of h(x) with respect to

x(k|k − 1) and R(k) is the sensor uncertainty, mod-

eled as a diagonal matrix.

From (9) and (13), the observations are associated

to their predictions in observation space. A statistical

ICINCO 2006 - ROBOTICS AND AUTOMATION

244

validation gate, the Mahalanobis distance, is used to

match observations. This distance γ is computed by

i,j

= ν

i,j

−1

(k) ν

i,j

, (14)

where S

(k) is the covariance related to the jth pre-

diction and ν

i,j

is the innovation vector, deﬁned as

i,j

= z

− h(

). (15)

If any prediction or observation is matched twice, it is

necessary to resolve the ambiguity. The method used

in the present work is the nearest neighbors data as-

sociation, in which the observation is matched against

the prediction with the smallest value N

i,j

= γ

i,j

+ ln |S

(k)|. (16)

If any match is found, not only the state is updated

but the uncertainty in both airship position and map

can be reduced, according to the following:

x(k) =

x(k|k − 1) + W(k)ν(k), (17)

P(k) = P(k|k − 1)

−W(k)S(k)W(k)

, (18)

where ν(k) is calculated from the union of the

matched predictions and observations, the gain ma-

trix W(k) is obtained from

W(k) = P(k|k − 1)∇h

(k)S

−1

(k) (19)

and S(k) is computed as in (13).

2.4.3 State Augmentation

The unmatched features must be included in the map,

in order for them to be used in the update stage the

next time they are observed. The process of incremen-

tally building the map is known as state augmentation

and is accomplished by the following equation:

aug

(k) = f

(x(k)) =

(k)

g(x

(k), z(k))

, (20)

with g(·, ·) deﬁned in (8). The newly added map fea-

ture is highly correlated to the vehicle state, due to the

fact that position and orientation uncertainty directly

affect the new landmark uncertainty. To accommo-

date that situation, the matrix P(k) must change ac-

cordingly:

aug

(k) = ∇f



P(k) 0

0 R(k)



∇f

(21)

With these equations, the cycle shown in ﬁgure 3

was fully described.

3 RESULTS

In this section, the described methodology is vali-

dated in simulation. The simulation setup and the per-

formance measurements are presented, as well as an

analysis of the results.

3.1 Simulation Setup

The SLAM implementation and studies reported here

were done in a simulation environment for the AS800

airship (Gomes and Ramos, 1998; de Paiva et al.,

1999). In the simulator, the airship 6DoF dynamics

are modeled according to

v = F

(v) + F

+ F

, (22)

where M is the mass matrix which includes both the

actual inertia of the airship and the virtual inertia ele-

ments associated with the dynamics of buoyant vehi-

cles; v = [ u, v, w, p, q, r ]

is the vector of the air-

ship linear and angular velocities; F

is the dynamics

vector containing the Coriolis and centrifugal force

terms, and also the wind-induced forces (Azinheira

et al., 2001); F

is the vector of aerodynamic forces

and moments; F

is the vector of propulsion forces

and moments, and F

represents the gravity forces

and moments.

In order to test the SLAM scheme in different con-

ditions during the simulated ﬂight, the airship is ex-

posed to mild wind and turbulence, also experiencing

different accelerations and turns. Lateral and longitu-

dinal control schemes are used to make the airship fol-

low a trajectory path deﬁned as a sequence of straight

lines between a set of pre-deﬁned points in latitude,

longitude and altitude. The lateral heading/guidance

control uses a PID controller as described in (Azin-

heira et al., 2000). The longitudinal control involves

an altitude state feedback controller with a propor-

tional plus derivative (PD) action, and a simple pro-

portional velocity controller (Bueno et al., 2002).

Virtual implementations of an IMU and a vision

system were developed so that the SLAM algorithms

could be effectively tested. The virtual IMU consists

simply of a module that collects the IMU perfect read-

ings, which are used to describe the error free path of

the airship, and adds a noise with the selected distri-

bution. The virtual vision system includes the simu-

lation of a camera, comprising focus, aspect and the

direction axes (which can be modiﬁed to reﬂect me-

chanical imperfections). With these parameters, im-

ages of the environment can be rendered in a visual-

ization frontend, as shown in Fig. 4. Also, it calcu-

lates the observations based in the environment math-

ematical representation, emulating an algorithm that

can return the relative position of the map landmarks

with respect to the camera. To this relative position, it

adds an error with known distribution to reﬂect other

noise sources.

Before starting the simulation, the airship is placed

at an arbitrary position in the virtual 3D world and the

initial estimate is set at the same pose. Because the

estimate and the map are made relative to the initial

setup of the system, the divergence between the real

TOWARDS A SLAM SOLUTION FOR A ROBOTIC AIRSHIP

245

Figure 4: Renderization of the virtual environment, display-

ing the airship in ﬂight and the landmarks on the ﬁeld.

state of the system and its estimate will directly show

the estimation error.

100

150

200

250

300

350

−200

−150

−100

−50

100

−1000

−500

500

1000

y axis

end →

x axis

← start

z axis

Figure 5: Comparison of the real trajectory (solid line) with

the one obtained from the IMU alone (dotted line). The

estimation diverges unconstrained.

As in the real onboard airship infrastructure (Bueno

et al., 2002; de Paiva et al., 2006), in the simulation

environment, new information from the virtual IMU

and vision system are provided every 0.05 seconds

(20 Hz). The IMU readings contain an error with dis-

tribution N (−0.03, 0.04) in m/s

in the linear accel-

eration f and N(0.01, 0.0025) rad/s in the angular

velocity ω, which means that both of them lead to a

serious drift that, if not corrected, accumulates over

time, generating ever increasing errors, as it is seen in

Fig. 5. The vision system makes observations of land-

marks (which are unknown to the vehicle system) and

detects their relative position with an additional error

with zero mean and a variance of 2.25 m in each of

the coordinates (x

, y

, z

3.2 SLAM System Performance

In what follows, localization and mapping results

of the proposed methodology are presented and dis-

cussed.

In terms of localization, Fig. 6 compares the path

followed by the airship during the experiment and the

trajectory computed by using the SLAM scheme. The

solid line represents the real position of the airship,

while the dotted line represents the estimate of the air-

ship position using the SLAM-EKF methodology. In

contrast to the IMU-only estimate shown in Fig. 5,

the estimation error does not grow indeﬁnitely and is

always small, considering the errors in both the IMU

and the vision system.

100

120

140

160

180

200

220

240

−150

−100

−50

100

end →

← start

x axis

y axis

z axis

Figure 6: Comparison of the real trajectory (solid line) with

its estimate, using the SLAM methodology (dotted line).

The generated map associated to the previous tra-

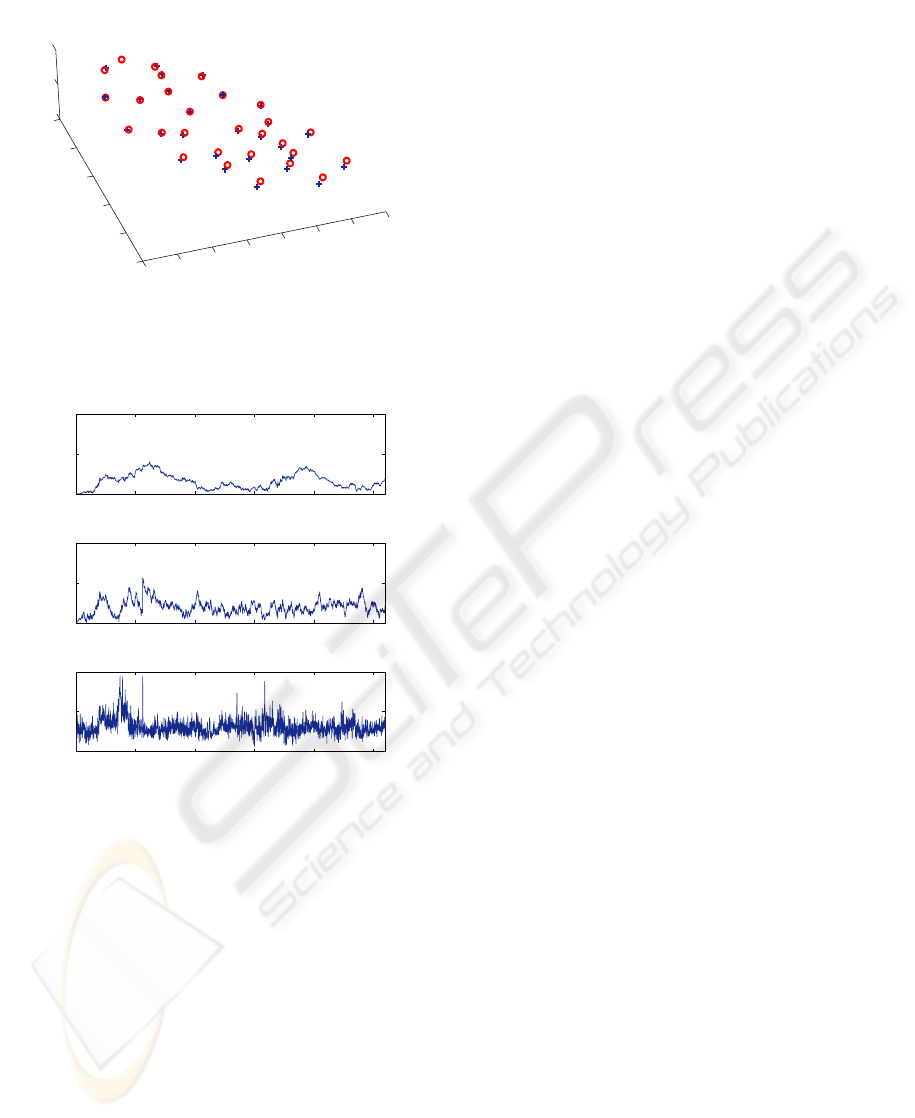
jectory is shown in Fig. 7. The circles represent the

position of the real landmarks, while the crosses show

the map estimate. As in the trajectory, the errors are

small. The mean distance from the estimates to the

real landmarks is 2.26 meters and the maximum dis-

tance is 4.59 m.

The error norm of the vehicle state, separated in

position, velocity and orientation, is shown in Fig.

8, and they demonstrate the overall SLAM conver-

gence. To understand the behavior of these errors

during some points of the ﬂight, it is necessary to an-

alyze the number of feature matches at each obser-

vation and the covariance of the map features. With

less than three matched features, the update stage will

not respond properly, as a unique position of the air-

ship with respect to the matched features cannot be

calculated. Also, when there are too many recently

discovered features being observed, their covariance

is high and the gain matrix W will not favor the up-

date, which means very quick turns and high speeds

will stop the system from working properly.

ICINCO 2006 - ROBOTICS AND AUTOMATION

246

100

150

200

250

300

350

−300

−200

−100

100

200

−40

−20

x axis

y axis

z axis

Figure 7: Real map, represented by circles, and the esti-

mated map, represented by crosses.

0 500 1000 1500 2000 2500

iteration

p error norm

0 500 1000 1500 2000 2500

0.5

iteration

v error norm

0 500 1000 1500 2000 2500

0.02

0.04

iteration

q error norm

Figure 8: On top is the position error norm. In the middle, it

is shown the velocity error norm. Bellow, is the orientation

quaternion error norm.

It is also important to point out that, even in ideal

conditions, the estimation system is always underde-

termined. If N features are matched, the dimension of

the 6Dof SLAM system is 9+3N, while the observa-

tions can provide rank 6 + 3N . This, however, does

not pose a problem to relative positioning and map-

ping. As the system converges, the errors related to

the landmarks will tend to zero, the airship pose with

respect to the map will be updated to its best and the

position of the landmarks will stop being corrected.

4 CONCLUSION

In this article, a methodology to estimate the AU-

RORA aerial platform position and attitude while in-

crementally building a map of the environment was

derived. A strategy to fuse the data provided by the

airship IMU and the vision system – which detects

the relative position between the landmarks and the

camera – using an extended Kalman ﬁlter was pre-

sented. The validation of the proposed methodology

was performed using a realistic simulation environ-

ment that includes the airship dynamic model and au-

tomatic trajectory control used in real ﬂights, a set of

virtual sensors and a visualization frontend.

The obtained results demonstrate the correctness of

the SLAM approach and constitute an important step

in the Project AURORA effort towards the incremen-

tal evolution of robotic airships. Considering the ex-

perimental validation objectives, the SLAM method-

ology hereby presented will be improved and inte-

grated to the airship embedded system for subsequent

experimental validation in real ﬂights. Considering

this objective, further work comprises: i) conclud-

ing the SLAM experiments with the real airship, de-

tecting simple artiﬁcial landmarks placed in the en-

vironment; ii) computational performance optimiza-

tions, aiming for larger maps and the simultaneous

observation of many landmarks; iii) a bearing-only

vision system, comprising a landmark tracking algo-

rithm and an efﬁcient feature initialization approach,

which will allow faster computation of the vehicle and

map state update (Davison, 2003); iv) a visual odom-

etry model where the relative motion of the airship

is recovered by decomposing the Euclidean homog-

raphy, established from projective geometry relation-

ships (Silveira et al., 2006).

ACKNOWLEDGEMENTS

The present work was sponsored by the Brazil-

ian agency FAPESP, under grants 04/13467-5 and

03/13845-7. The authors thank Dr. Ely Paiva, for

his support concerning the airship dynamic model and

control strategies, and Dr. Paulo Valente for his assis-

tance regarding Mr. Castro’s M.Sc. work.

REFERENCES

Azinheira, J. R., de Paiva, E. C., Ramos, J. G., Bueno, S. S.,

and Bergerman, M. (2001). Extended dynamic model

for aurora robotic airship. In 14th AIAA Lighter-Than-

Air Systems Technology Conference.

Azinheira, J. R., de Paiva, E. C., Ramos, J. J. G., and

Bueno, S. S. (2000). Mission path following for an

TOWARDS A SLAM SOLUTION FOR A ROBOTIC AIRSHIP

247

autonomous unmanned airship. In International Con-

ference on Robotics and Automation, San Francisco,

USA.

Bailey, T. (2002). Mobile Robot Localisation and Mapping

in Extensive Outdoor Environments. PhD thesis, Aus-

tralian Centre for Field Robotics, University of Syd-

ney.

Bueno, S. S., Azinheira, J. R., Ramos, J. G., de Paiva,

E. C., Rives, P., Elfes, A., Carvalho, J. R. H., and Sil-

veira, G. F. (2002). Project aurora - towards an au-

tonomous robotic airship. In Workshop on Aerial Ro-

botics. IEEE International Conference on Intelligent

Robot and Systems, Lausanne, Switzerland.

Castellanos, J. A., Montiel, J. M. M., Neira, J., and Tards,

J. D. (1999). The spmap: A probabilistic framework

for simultaneous localization and map building. IEEE

Transactions on Robotics and Automation.

Castellanos, J. A., Neira, J., and Tards, J. D. (2001). Mul-

tisensor fusion for simultaneous localization and map

building. IEEE Transactions on Robotics and Automa-

tion.

Davison, A. (2003). Real-time simultaneous localisation

and mapping with a single camera. In Ninth Intl. Con-

ference on Computer Vision.

de Paiva, E. C., Azinheira, J. R., Ramos, J. G., Moutinho,

A., and Bueno, S. S. (2006). Project aurora: in-

frastructure and ﬂight control experiments for a ro-

botic airship. Journal of Field Robotics. In press.

de Paiva, E. C., Bueno, S. S., Gomes, S. B. V., Ramos, J.

J. G., and Bergerman, M. (1999). A control system de-

velopment environment for aurora’s semi-autonomous

robotic airship. In Int. Conference on Robotics and

Automation.

Elfes, A. (1987). Sonal-based real-world mapping and nav-

igation. IEEE Journal of Robotics and Automation.

Elfes, A. (1989). Occupancy Grids: A Probabilistic Frame-

work for Robot Perception and Navigation. PhD the-

sis, Department of Electrical and Computer Engineer-

ing, Carnegie Mellon University.

Elfes, A., Bueno, S. S., Bergerman, M., and Ramos, J. J. G.

(1998). A semi-autonomous robotic airship for envi-

ronmental monitoring missions. In Int. Conf. on Ro-

botics and Automation.

Elfes, A., Bueno, S. S., Bergman, M., de Paiva, E. C.,

Ramos, G. J., and Azinheira, J. R. (2003). Robotic

airships for exploration of planetary bodies with an

atmosphere: Autonomy challenges. Autonomous Ro-

bots.

Gomes, S. B. V. and Ramos, J. J. G. (1998). Airship

dynamic modeling for autonomous operation. In

Int. Conference on Robotics and Automation, Leuven,

Belgium.

Guivant, J. and Nebot, E. (2001). Optimization of the simul-

taneous localization and map-building for real-time

implementation. IEEE Transactions on Robotics and

Automation.

Guivant, J. and Nebot, E. (2003). Solving computational

and memory requirements of feature-based simultane-

ous localization and mapping algorithms. IEEE Trans-

actions on Robotics and Automation.

Hygounenc, E., Jung, I., Soures, P., and Lacroix, S. (2004).

The autonomous blimp project of laas-cnrs: achieve-

ments in ﬂight control and terrain mapping. Intl. Jour-

nal of Robotics Research.

Kantor, G., Wettergreen, D., Ostrowski, J., and Singh, S.

(2001). Collection of environmental data from and air-

ship platform. In SPIE Conference on Sensor Fusion

and Decentralized Control in Robotic Systems IV.

Kim, J. (2004). Autonomous Navigation for Airborne Ap-

plications. PhD thesis, Australian Centre for Field Ro-

botics, University of Sydney.

Langelaan, J. and Rock, S. (2005). Towards autonomous

uav ﬂight in forests. In AIAA Guidance, Navigation

and Control Conference.

Panzieri, S., Pascucci, F., and Ulivi, G. (2002). An out-

door navigation system using gps and inertial plat-

form. IEEE/ASME Transactions on Mechatronics.

Ruiz, I. T., Pelillot, Y., Lane, D. M., and Salson, C. (2001).

Feature extraction and data association for auv con-

current mapping and localisation. In IEEE Interna-

tional Conference on Robotics and Automation.

Silveira, G., Malis, E., and Rives, P. (2006). Visual servo-

ing over unknown, unstructured, large-scale scenes. In

IEEE International Conference on Robotics and Au-

tomation, Orlando, USA.

Smith, R., Self, M., and Cheeseman, P. (1987). A stochas-

tic map for uncertain spatial relationships. In Fourth

International Symposium on Robotics Research.

Smith, R., Self, M., and Cheeseman, P. (1988). Estimat-

ing uncertain spatial relationships in robotics. In Au-

tonomous Robot Vehicles. Springer Verlag.

Sukkarieh, S., Nebot, E., and Durrant-Whyte, H. (1999).

A high integrity imu/gps navigation loop for au-

tonomous land vehicle applications. IEEE Transac-

tions on Robotics and Automation.

Wimmer, D., Bildstein, M., Well, K. H., Schlenker, M.,

Kingl, P., and Krplin, B. (2002). Research airship

”lotte”: development and operation of controllers for

autonomous ﬂight phases. In IEEE/RSJ Int. Confer-

ence on Intelligent Robots and Systems.

Wu, A., Johnson, E., and Proctor, A. (2005). Vision-aided

inertial navigation for ﬂight control. In AIAA Guid-

ance, Navigation and Control Conference.

ICINCO 2006 - ROBOTICS AND AUTOMATION

248