TIMED DISCRETE-EVENT SYSTEM SUPERVISORY CONTROL

FOR UNDER-LOAD TAP-CHANGING TRANSFORMERS

A. Afzalian

Department of Control Systems Engineering, Shahid Abbaspour University of Technology,

PO Box 16765-1719, Tehran, Iran

A. Saadatpoor and W. M. Wonham

Department of Electrical and Computer Engineering, University of Toronto

10 King’s College Road Toronto, Ontario M5S3G4, Canada

Keywords:

Supervisory Control, Timed Discrete-Event Systems, Automatic Voltage Control, Tap-Changer Transformer.

Abstract:

Timed discrete-event systems (TDES) have so far not been used for modelling and control of electrical power

system. Since these systems have both logical and temporal behavior, we propose to use TDES to address

their control problems. Under-load tap-changing transformers (ULTC) which obviously have discrete-event

behavior are widely used in transmission systems to take care of instantaneous variations in the load conditions

in substations. ULTC may be controlled either automatically or manually. This paper discusses the modelling

and synthesis of a timed discrete-event system supervisory controller for ULTC. Different modes of operation

are considered and it is shown that the speciﬁcations are controllable and the closed loop control system is

non-blocking. Protective system designers in electrical power systems can use the proposed approach to verify

their required temporal and logical behavior.

1 INTRODUCTION

In the last two decades, Discrete Event Systems

(DES) have been studied by researchers from differ-

ent ﬁelds, with respect to modeling, analysis and con-

trol. Several models have been proposed and inves-

tigated. These models can be classiﬁed as untimed

DES models and timed DES models.

In an untimed model, when considering the state evo-

lution, only the sequence of states visited is of con-

cern. That is, we are only interested in the logical

behavior of the system.

In a timed model, both logical behavior and timing

information are considered. Brandin and Wonham

(Brandin and Wonham, 1994) adjoin to the struc-

ture of (Ramadge and Wonham, 1987) the timing

features of timed transition models (TTM)(Ostroff,

1990). The BW framework, which we use in this

paper, retains the concept of maximally permissive

supervision introduced in (Ramadge and Wonham,

1987) , allows the timed modelling of DES, admits

subsystem composition, and admits forcing and dis-

ablement as means of control.

In the Ramadge-Wonham framework(Ramadge and

Wonham, 1987), an automaton (in practice, ﬁnite) is

used to model both the plant to be controlled and the

speciﬁcation. The RW approach successfully treats

the existence and theoretical synthesis procedure of

the nonblocking supervisory controller. Different

synthesis methods have been developed and imple-

mented as software TCT (Wonham, 2005) for un-

timed models and TTCT (Wonham, 2005) for timed

models to compute controllers that are optimal in the

sense that the controlled system not only satisﬁes the

speciﬁcations but is also as permissive as possible.

Electrical power systems frequently exhibit inter-

actions between continuous dynamics and discrete

events. The power system, in its simplest represen-

tation, comprises a set of lines intersecting at nodes

(buses). Energy is injected at buses by generators,

and loads can be considered as negative injections.

The ﬂow of power along lines to and from buses is a

phenomenon of primary interest in power system op-

eration and control. Transformers with tap-changing

facilities constitute an important means of control-

ling voltage throughout electrical power systems at

all voltage levels. Transformers with off-load tap-

changing facilities can help to maintain satisfactory

voltage proﬁles, while under-load tap-changing trans-

formers (ULTC) can be used to take care of daily,

hourly, and minute-by-minute variations in system

conditions. ULTC may be controlled either automati-

cally or manually (Kundur, 1994).

Since emergence of DES, they have been applied to

Afzalian A., Saadatpoor A. and M. Wonham W. (2006).

TIMED DISCRETE-EVENT SYSTEM SUPERVISORY CONTROL FOR UNDER-LOAD TAP-CHANGING TRANSFORMERS.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 85-90

DOI: 10.5220/0001213400850090

 SciTePress

some problems in electrical power systems (Prosser,

1995)(Lin et al., 2004)(Afzalian and Wonham, 2006).

These applications include: supervisory control,

modelling and analysis, and monitoring and diagno-

sis of power systems. The present paper discusses

the timed DES approach to design a supervisory con-

trol for ULTC. Section 2 reviews the supervisory con-

trol of timed DES. Tap-changing transformers and the

logic for controlling the feeder voltage are discussed

in section 3. A typical tap-changer and a set of con-

trol speciﬁcations are also modeled as some automata

in section 3. The TDES models of the plant and con-

trol speciﬁcation have been used to synthesize non-

blocking optimal supervisors for the tap-changer in

different modes of operation in section 4 as an imple-

mentation study.

2 SUPERVISORY CONTROL OF

TDES

In this section, we brieﬂy review the TDES model

proposed by Brandin and Wonham (Brandin and

Wonham, 1994). First, we introduce a ﬁnite automa-

ton G

act

= (A, Σ

act

, δ

act

, a

, A

), called an activ-

ity transition graph (ATG) to describe the untimed be-

havior of the system. In G

act

, A is the ﬁnite set of ac-

tivities, Σ

act

is the ﬁnite set of events, a partial func-

tion δ

act

: A × Σ

act

−→ A is the activity transition

function, a

∈ A is the initial activity, and A

⊆ A

is the set of marked activities.

In order to construct a TDES model, timing infor-

mation is introduced into G

act

. Let N denote the

nonnegative integers. In Σ

act

, each event σ will be

equipped with a lower time bound l

∈ N and an up-

per time bound u

∈ N ∪ {∞} such that l

≤ u

Then the set of events is decomposed into two sub-

sets Σ

spe

= {σ ∈ Σ

act

∈ N} and Σ

rem

= {σ ∈

act

= ∞}. The lower time bound would typi-

cally represent a delay, while an upper time bound is

a hard deadline.

For each σ ∈ Σ

act

, the timer interval T

is deﬁned as



[0, u

] if σ ∈ Σ

spe

[0, l

] if σ ∈ Σ

rem

. The TDES deﬁned

by Brandin and Wonham (Brandin and Wonham,

1994) is a ﬁnite automaton G = (Q, Σ, δ, q

, Q

)

which can be displayed by its timed transition graph

(TTG). The state set Q is deﬁned as Q = A ×

|σ ∈ Σ

act

}. A state q ∈ Q is of the form q =

(a, {t

|σ ∈ Σ

act

}), where a ∈ A and t

∈ T

. The

initial state q

∈ Q is deﬁned as q

= (a

, {t

σ,0

|σ ∈

act

}), where t

σ,0



, if σ ∈ Σ

spe

, if σ ∈ Σ

rem

. The

set Q

⊆ Q is given by a subset of A

|σ ∈

act

}. The event set Σ is deﬁned as Σ = Σ

act

∪

{tick},where the additional event tick represents the

passage of one time unit. The state transition func-

tion δ : Q × Σ −→ Q is deﬁned as follows. For any

σ ∈ Σ and any q = (a, {t

|τ ∈ Σ

act

}) ∈ Q, δ(q, σ)

is deﬁned, written δ(q, σ)!, if and only if one of the

following conditions holds:

• σ = tick and ∀τ ∈ Σ

spe

; δ

act

(a, τ )! ⇒ t

> 0

• σ ∈ Σ

spe

and δ

act

(a, σ)! and 0 ≤ t

≤ u

− l

• σ ∈ Σ

rem

and δ

act

(a, σ)! and t

= 0

When δ(q, σ)!, q

′

= δ(q, σ) = (a

′

, {t

′

|τ ∈ Σ

act

}) is

deﬁned as follows:

• if σ = tick then a

′

= a and for all τ ∈ Σ

act

′



− 1, if δ

act

(a, τ )! and t

> 0

, otherwise

• if σ ∈ Σ

act

then a

′

= δ

act

(a, σ), t

′

= t

σ,0

, and for

τ ∈ Σ

act

if τ 6= σ then

′



, if δ

act

′

, τ )!

τ,0

, otherwise

Let Σ

∗

be the set of all ﬁnite strings of elements in

Σ, including the empty string ε. The function δ is

extended to δ : Q × Σ

∗

→ Q in the natural way.

The closed behavior, the strings that are generated by

G, and marked behavior, the strings that are gener-

ated by G and lead to a marker state, of the TDES

G are deﬁned by L(G) = {s ∈ Σ

∗

| δ(q

, s)!} and

(G) = {s ∈ Σ

∗

| δ(q

, s) ∈ Q

}, respectively.

G is called nonblocking if

(G) = L(G).

As in untimed supervisory control, the set Σ

act

is par-

titioned into two subsets Σ

and Σ

of controllable

and uncontrollable events. An event σ ∈ Σ

act

that

can preempt the event tick is called a forcible event.

The set of forcible events is denoted by Σ

for

. A

forcible event can be either controllable or uncontrol-

lable. By forcing an enabled event in Σ

for

to occur,

we can disable the event tick. In this framework a su-

pervisor repeatedly decides to disable or enable each

event in Σ

∪ {tick}.

The simplest way to visualize the behavior of a TDES

G under supervision is ﬁrst to consider the inﬁnite

reachability tree of G before any control is opera-

tive (Wonham, 2005). Each node of the tree corre-

sponds to a unique string s of L(G). At each node

of the tree we can deﬁne the subset of eligible events

by Elig

(s) := {σ ∈ Σ| sσ ∈ L(G)}. In order

to deﬁne the notion of controllability we consider a

language K ⊆ L(G) and write Elig

(s) := {σ ∈

Σ| sσ ∈

K)}. K is controllable with respect to G if,

for all s ∈

Elig

(s) ⊇



Elig

(s) ∩ (Σ

∪ {tick}), Elig

(s) ∩ Σ

for

= ∅

Elig

(s) ∩ Σ

, Elig

(s) ∩ Σ

for

6= ∅

Our control objective is, for the given plant lan-

guage L(G

) and the speciﬁcation language L(G

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

to ﬁnd a supervisor such that the closed loop lan-

guage is, in the sense of set inclusion, the largest

sublanguage of L

) ∩ L

) which is con-

trollable w.r.t G

and also nonblocking, written

supC(L

), L

)).

3 TAP-CHANGING

TRANSFORMERS

Transformers with tap-changing facilities constitute

an important means of controlling voltage throughout

electrical power systems at all voltage levels. Trans-

formers with ULTC are widely used in transmission

systems. For example, Ontario Hydro provided ULTC

facilities on most 500/230 kV autotransformers and

on all “area supply” transformers stepping down from

230 kV or 115 kV to 44 kV, 27.6 kV, or 13.8 kV (Kun-

dur, 1994). Whereas many articles considered ULTC

as a nonlinear element in the power system model for

voltage stability studies, a model in Petri net form

for tap-changer has been used in a framework of dif-

ferential, switched algebraic and state-reset equations

(Hiskens and Sokolowski, 2001).

3.1 Tap-Changer Control Logic

The control logic for tap-changer transformers can be

found in the literature (Kundur, 1994),(Ohtsuki et al.,

1991),(Otomega et al., 2003) as well as in manufac-

turers’ catalogues (e.g. (GE, 2005))in different detail.

The ULTC control logic can be summarized as fol-

lows. When the voltage is not “normal” ( i.e. is out-

side a desired limit) then the controller changes tap

ratio after a time delay to restore the voltage i.e. bring

it back into its dead-band. The delay time is used to

prevent unnecessary tap changes in response to tran-

sient voltage variations and to introduce the desired

time delay before a tap movement. Existence of this

delay in temporal behavior of the LTC motivates us-

ing TDES framework for this control problem.

3.2 TDES Modelling of the Plant

In this section the timed DES models of the plant and

the control logic governing the ULTC are discussed.

The models will be used later to study implementa-

tion of supervisory controller.

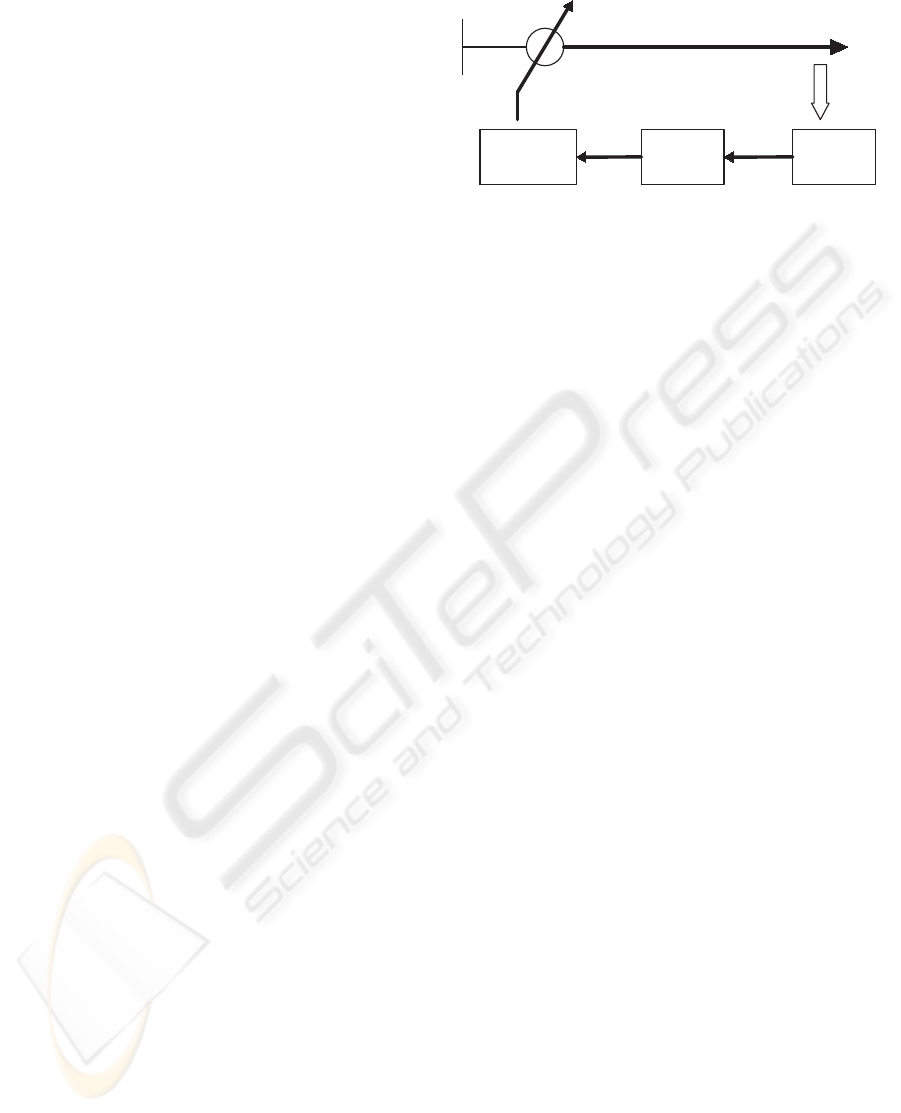
The block diagram of the control system for auto-

matic changing of transformer taps is shown in Figure

1. Each component is modeled as a TDES. Then the

TDES models of the plant components are composed

to form the plant model.

As discussed in Section 2, we ﬁrst model the

system components by the corresponding ATGs for

Voltage

Sensor

Tap-Changing

Motor

Supervisory

controller

Source

Feeder

Figure 1: Block diagram of control system for automatic

changing of transformer taps.

their untimed behavior. For adding time features we

deﬁne the time bounds (lower and upper) for the

events of the system. The plant consists of two main

components:

- Voltmeter

The load voltage must be within a dead-band

± ID). where V

is “set point”,V

is “(measured)

Load Voltage”, △V = V

−V

is “Voltage Deviation”

and ID is “Insensitivity Degree” which is deﬁned

as the maximum admissible variation of the voltage

before originating a command to change the tap.

Voltmeter reports events associated with the load

voltage using these events :

Initialize Voltmeter (ev11 , [0,inf])

Report |△V | > ID and △V > 0 (ev12 , [0,inf])

Report |△V | > ID and △V < 0 (ev14 , [0,inf] )

Report |△V | < ID— i.e. Voltage Recovered (ev16 ,

[0,inf])

Report Voltage exceeds V

max

(ev18 , [0,inf])

- Tap Changer

The transformer tap changer controls the transformer

ratio “manually” or “automatically” in order to keep

the power supply voltage practically constant, inde-

pendently of the load. If the tap increase (decrease)

is successful, the system returns to a state and waits

for another command. If the tap increase (decrease)

operation fails, the controller changes to the Manual

mode, and waits for another command.

It is assumed here that the tap-changer has 5 steps.

Events associated with the Tap Changer are:

Tap up command (ev31 [5, inf] ),

Tap up successful (ev30 [0, inf] ),

Tap up failed (ev32 [0, inf]),

Tap down command with 5s delay (ev33 [5, inf]),

Tap down command without delay (ev35 [0, inf]),

Tap down successful (ev34 [0, inf]),

Tap down failed (ev36 [0, inf]).

The ATGs for the voltmeter and tap changer are

shown in Figure 2. In order to ﬁnd the whole sys-

tem’s model, we ﬁrst ﬁnd the composition (analogous

to synchronous product in untimed DES) of the ATGs

TIMED DISCRETE-EVENT SYSTEM SUPERVISORY CONTROL FOR UNDER-LOAD TAP-CHANGING

TRANSFORMERS

of the system, then ﬁnd the TTG of the plant by con-

verting the ATG to TTG.

31

30

33,35

34

36

32

11

12,14,16,18

(a)

(b)

Figure 2: ATGs for (a) Voltmeter (b) Tap Changer.

3.3 TDES representation of Control

Speciﬁcations

There are two modes of operation: “Automatic” and

“Manual”.

1) Automatic Mode

The tap-changer works in Automatic mode according

to the following logic (control speciﬁcations):

a. If the voltage deviation |△V | > ID and △V is

Negative (ev14) then the timer will start and when it

times out i.e. the time delay in occurrence of ev31

elapses then a “tap increase ” event (ev31) will occur

and the timer will reset.

b. If the voltage deviation |△V | > ID and △V is

Positive (ev12) then the timer will start and when it

times out then a “tap decrease ” (ev33) will occur and

the timer will reset.

c. If the voltage returns to the dead-band (ev16), be-

cause of smooth system dynamics or a tap change or

some other system events, then no tap change will oc-

cur.

d. If the voltage exceeds the value set for ”Quick

Lowering” (ev18), then the lowering tap command

without delay (ev35) happens instantaneously.

Figure 3 shows the TDES model of the control

speciﬁcation in the Automatic mode. It actually im-

plements all the above logic in a single TDES. We

should mention that because in these speciﬁcations

we need the events tap up/down command ( 31,33,35)

to preempt tick in some states of the speciﬁcation

TDES, we should deﬁne these events as “forcible”

events. (Section 2 )

31,

16

tt t

33,

16

t

tttt t

16 16 16 16

16

14

12

3518

16

t

1616

16

Figure 3: TTG of the control speciﬁcations in Automatic

Mode.

2) Auto/Manual Mode

In this mode of operation, we need a model for the

operator action to switch the modes and to override in

abnormal situations. Events 41 and 43 are deﬁned for

operator actions:

Enter “Automatic” Mode (ev41, [0,inf]),

Enter “Manual” Mode (ev43, [0,inf])

The operator can force the system from Automatic to

Manual mode at any time (ev43). System switches

to Manual mode from Automatic mode by a “Man-

ual” command from operator (ev43), or an abnormal

situation such as, failed tap up/tap down. In manual

mode the system is waiting for “Tap-up”, “Tap-down”

or “Automatic” commands. On returning to Auto-

matic mode the controller is reinitialized at state 0 of

the Automatic speciﬁcation (Fig. 3). A speciﬁcation

for the Auto/Manual mode (SPEC2) can be achieved

by inserting suitable transitions after the occurrence

of ev31 and ev33 and also by adding a new state as

the “Manual-operation” state. The “Manual” com-

mand (ev43) takes the system from any state (*) to

the Manual-operation state. Then ev41 takes this state

back to the initial state. Fig. 4 shows the TDES model

(TTG) for the control speciﬁcation in Auto/Manual

mode.

4 IMPLEMENTATION STUDY

The plant and the speciﬁcation TDES models are im-

plemented in the TTCT software. The supervisory

controller has been designed for the Automatic and

Auto/Manual modes of operation separately.

A. Automatic Mode

The supervisor and the control data for the ULTC in

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

tt t t

tttt t

16 16 16

16

14 12

35

18

16

t

1616

16

1616

34

36

31

32

30

36

34

33

41

*

43

Figure 4: TTG of the control speciﬁcations in Auto/Manual

Mode. The transition 43 from * represent similar transitions

from all states to the “manual operation” state.

the Automatic mode are calculated using TTCT.

SUPER1 = Supcon(PLANT1,SPEC1) (199,301)

MINSUPER1 = Minstate(SUPER1) (52,79)

So we have found a supervisory controller for the

Automatic mode of operation with 52 states and 79

transitions.

B. Auto/Manual Mode

The operator override is incorporated in the model

by the control speciﬁcation shown in Figure 4. Using

this speciﬁcation and the new plant model which

is composed by the “Operator” ATG (which has

one state and two transitions i.e. 41 and 43 ), the

supervisory control is synthesized:

SUPER2 = Supcon(PLANT2,SPEC2) (233,547)

MINSUPER2 = Minstate(SUPER2) (56,130)

PMINSUP = Project(MINSUPER2, ‘tick’) (26,53)

As can be seen, the supervisor state-transition size is

(56,130) after applying the “Minstate” operation. By

projecting out tick from the supervisor we can dis-

play its transition structure as the timed activity transi-

tion graph (TATG)(Wonham, 2005). While the TATG

suppresses tick, it does incorporate the constraints on

ordering of activities induced by time bounds. The

TATG of the supervisor for Auto/Manual mode is

shown in Figure 5.

5 CONCLUSION

Synthesis of timed discrete-event based supervisory

control for a tap-changing transformer was discussed

in this work. The tap-changer components and its

logical and temporal behavior have been modeled as

TDES. Controllability of the speciﬁcation is evalu-

ated and supervisory controllers have been designed

for two different modes of operation using the TTCT

software. It is guaranteed by the synthesis procedure

that the designed supervisors are optimal and non-

blocking. The state size of the supervisory controller

has been reduced for easier implementation. The fol-

lowing topics can be considered for future research

work:

- Implementation of the synthesized supervisory con-

troller on programmable logic controllers (PLC).

- Construction of a hierarchical framework for the

supervisory control problem in a micro-grid electrical

power system containing a tap-changer transformer

and other discrete and continuous elements.

REFERENCES

Afzalian, A. and Wonham, W. M. (2006). Discrete-event

system supervisory controller design for an electrical

power transmission network. In 14th Iranian Confer-

ence on Electrical Engineering (ICEE’06), Tehran.

Brandin, B. and Wonham, W. M. (1994). Supervisory con-

trol of timed discrete event systems. IEEE Transac-

tions on Automatic Control, 39(2):329–342.

GE (2005). Consumer Industrial, DTR - Digital

Tap Changer Controller Instruction Manual GEK-

106305A. p. 7-12.

Hiskens, I. A. and Sokolowski, P. J. (2001). System-

atic modeling and symbolically assisted simulation of

power systems. IEEE Transactions on Power Systems,

16(2): p. 229-234.

Kundur, P. (1994). Power System Stability and Control.

McGraw-Hill.

Lin, S.-Y., Ho, Y.-C., and Lin, C. I.-H. (2004). An ordinal

optimization theory-based algorithm for solving the

optimal power ﬂow problem with discrete control vari-

ables. IEEE Transactions on Power Systems, 19(1): p.

276-286.

Ohtsuki, H., Yokoyama, A., and Sekine, Y. (1991). Reverse

action of on-load tap changer in association with volt-

age collapse. IEEE Transactions on Power Systems,

6(1): p. 300-306.

Ostroff, J. S. (1990). Deciding properties of timed transi-

tion models. IEEE Transactions on Parallel and Dis-

tributed Systems, 1(2):170–183.

Otomega, B., Sermanson, V., and Cutsem, T. V. (2003).

Reverse-logic control of load tap changers in emer-

gency voltage conditions. in Proceedings of Power

Tech Conference, Bologna.

Prosser, J. (1995). Supervisory control of electric power

transmission networks. IEEE Transactions on Power

Systems, 10(2): p. 1104-1110.

Ramadge, P. J. and Wonham, W. M. (1987). Supervisory

control of a class of discrete event processes. SIAM J.

Contr. Optim., 25(1):206–230.

Wonham, W. M. (2005). Supervisory Control of Discrete-

Event Systems. Department of Electrical and Com-

puter Engineering, University of Toronto, available at

http://www.control.utoronto.ca/DES.

TIMED DISCRETE-EVENT SYSTEM SUPERVISORY CONTROL FOR UNDER-LOAD TAP-CHANGING

TRANSFORMERS

Figure 5: TATG of the supervisory controller for Auto/Manual mode of operation.

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL