
GLOBAL OPTIMIZATION OF PERFORMANCE OF A 2PRR
PARALLEL MANIPULATOR FOR COOPERATIVE TASKS *
Héctor A. Moreno, J. Alfonso Pámanes
Instituto Tecnológico de la Laguna (ITLag), Blvd. Revolución y Cuauhtémoc; Torreón, México
Philippe Wenger, Damien Chablat
Institut de Recherche en Communications et Cybernétique de Nantes (IRCCyN), BP 92101
44321 Nantes CEDEX 3 France
Keywords: Optimization of performance, parallel manipulators, cooperative manipulators, trajectory planning.
Abstract: In this paper the trajectory planning problem is solved for a 2P
RR parallel manipulator which works in
cooperation with a 1 degree-of-freedom (dof) platform. The whole kinematic chain is considered as a
redundant 3-dof manipulator, and an algorithm is presented to solve the redundancy by using the joint
velocities in the null space of the jacobian matrix. The internal motion of the assisted manipulator allows
globally optimize the condition number of the jacobian matrix during the accomplishment of a desired task.
Consequently, the accuracy of the manipulator is maximized and singular or degenerate poses are avoided.
A case of study is presented to show the effectiveness of our approach.
1 INTRODUCTION
A parallel manipulator is a linkage mechanism
whose end-effector is connected to a fixed frame
through several independent kinematic chains. For
certain applications the parallel manipulators have
particularly interesting features. In fact, because of
the significant global rigidity of parallel
manipulators, they become more efficient for
machining applications than serial manipulators.
Nevertheless, the workspace of a parallel
manipulator is typically too small for such
applications. This handicap, however, can be
overcame by incorporating a secondary cooperative
manipulator to aid the main one (the parallel) to
achieve the task. The secondary manipulator should
continuously relocate the work-piece to the main one
in such a way that the kinematic performance of the
chain is enhanced.
The strategy in which a positional device is
incorporated to aid a main manipulator has been
applied in previous works. In one paper (Hemmerle
and Prinz, 1991) the main manipulator was
redundant, and the secondary was non redundant.
Both manipulators cooperate to achieve a welding
task: the main one (right hand) moves the welding
torch and the positioner (left hand) continuously
relocates the work-pieces. The redundancy should be
solved for the main manipulator whereas a suitable
trajectory of the positioner must be established. The
solution to both problems was based on two criteria:
in the former, the joint variables are moved as far as
possible from its limits; in the second criterion, the
joint displacements are minimized. The approach
proposed in the aforementioned reference was not
extended for parallel manipulators. Works were not
found dealing with the synthesis of trajectories of
cooperative parallel manipulators.
The trajectory planning problem of a 2P
RR
parallel manipulator operating in cooperation with a
1 dof platform is studied in this paper. A formulation
is proposed to solve the problem in such a way that a
manipulator’s kinetostatic index of performance is
optimized during the achievement of a desired task.
In our formulation the whole kinematic chain is
considered as being equivalent to a redundant three
degree-of-freedom manipulator. Then, the joint
* Research completed by the IRCCyN and the ITLag in the
Franco-Mexican Laboratory of Applied Automatics
(
LAFMAA) and supported by the CNRS and the CONACYT.
516
A. Moreno H., Alfonso Pámanes J., Wenger P. and Chablat D. (2006).
GLOBAL OPTIMIZATION OF PERFORMANCE OF A 2PRR PARALLEL MANIPULATOR FOR COOPERATIVE TASKS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 516-522
DOI: 10.5220/0001213505160522
Copyright
c
SciTePress
velocities in the null space of the Jacobian matrix are
used to globally optimize both the manipulability
and the condition number of the manipulator.
2 THE 2-DOF ORTHOGLIDE
MANIPULATOR
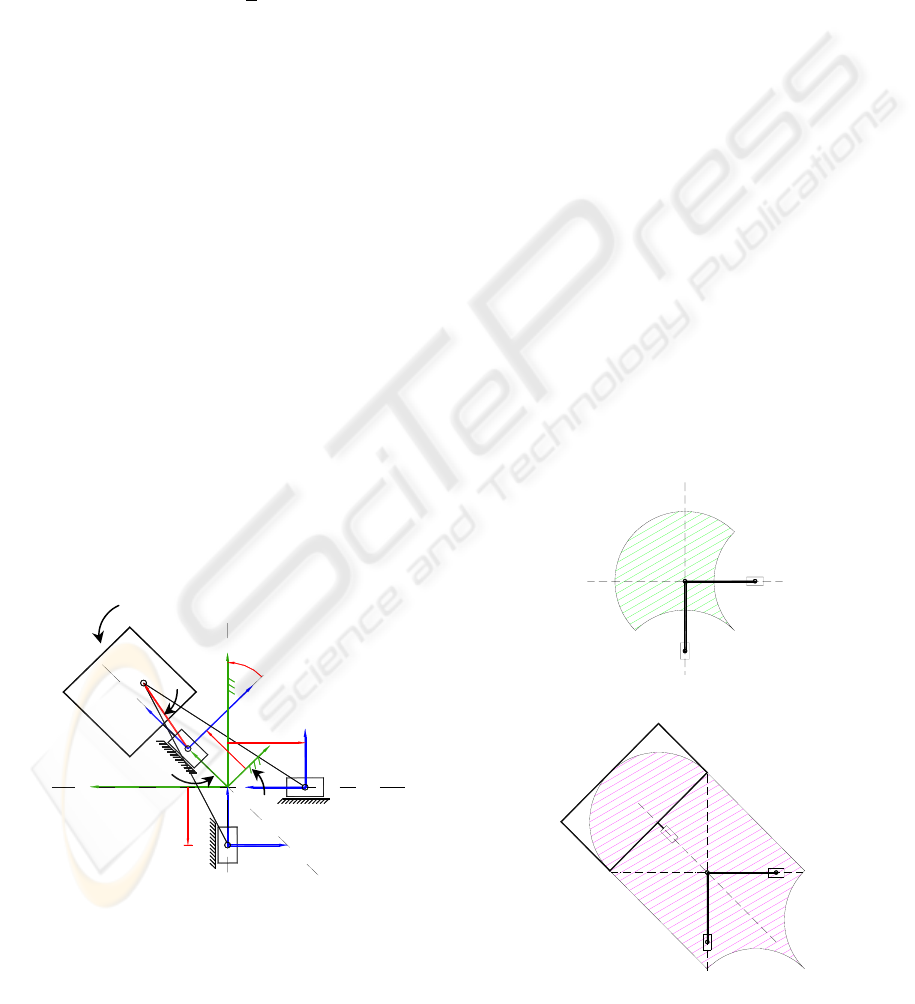
A kinematic scheme of the 2PRR manipulator and
the cooperative platform is presented in Figure 1. As
observed, the manipulator is composed of two
actuated sliding blocks which are coupled to the
fixed frame. On the other hand, the blocks are
connected to the links AC and BC by the revolute
joints A and B, respectively. Such links are finally
connected by the revolute joint C. All the revolute
joints are passives. The axes of the prismatic joints
are orthogonal. This mechanism, termed 2-dof
Orthoglide, has been analyzed in previous works
(Wenger et. al., 2001; Majou et. al., 2002).
We consider the lengths of bars AC and BC as
being L=1 m. The values of the joint variables are
constrained as follows:
m11-
1
≤≤
ρ
,
m1.50
2
≤≤
ρ
and
m1.50
3
≤≤
ρ
. These intervals define the
domain of admissible configurations in the joint
space of the manipulator.
We assume that the tasks to be carried out by the
2-dof Orthoglide are in machining operations. So, in
order to enlarge its workspace, we integrate a
cooperative manipulator which should move the
work-pieces. This secondary manipulator consists of
a 1-dof table having translational motion on an axis
whose direction is defined by θ
1
in Figure 1.
3 KINEMATICS AND
SINGULARTIES OF THE
MANIPULATOR
It can be observed in Figure 2 that the manipulator’s
workspace is increased by incorporating a
cooperative platform. By doing this, however, the
trajectory planning of the manipulator in
coordination with the platform becomes a complex
issue. Indeed, from the point of view of the relative
motion manipulator-platform, the manipulator
becomes kinematically redundant; i.e. that infinity of
relative motions between the manipulator and the
platform allow the achievement of the task. Thus, an
optimal solution should be found in order to solve
the redundancy. In this paper, the parallel
manipulator with the cooperative platform will be
termed assisted manipulator.
3.1 Kinematics of the Assisted
Manipulator
The joint and operational velocities vectors,
•
ρ
and
t, respectively, of a parallel manipulator are related
as follows:
•
= ρBAt
(1)
m1.50
2
≤≤
ρ
m1.50
3
≤≤
ρ
m 11-
1
≤≤
ρ
m1.50
2
≤≤
ρ
m1.50
3
≤≤
ρ
(a) Without cooperative platform.
(b) With a cooperative platform.
Figure 2: Workspace of the 2 dof Orthoglide Manipulator.
1
θ
1'
y
1'
x
0
c
r
0
y
0
x
1
x
1
y
A
B
C
ρ
1
ρ
2
ρ
3
Figure 1: Kinematic scheme of the 2 dof Orthoglide
manipulator.
Cooperative platform
GLOBAL OPTIMIZATION OF PERFORMANCE OF A 2PRR PARALLEL MANIPULATOR FOR COOPERATIVE
TASKS
517

In Equation 1, A and B are, respectively, the
parallel and serial Jacobian matrices, (Gosselin and
Angeles, 1990). The entries of these matrices depend
on both the design variables and manipulator pose.
For the assisted manipulator, the joint velocity
vector is given by
[]
123
T
ρρρ
=ρ
and the
operational velocity vector is
T
][t
cycx
r,r
••
=
. The
scalars r
cx
and r
cy
are the orthogonal components of
the position vector
0
r
c
(corresponding to point C)
referred to a frame x
0
-y
0
attached to the translational
platform (Figure 1). For the assisted manipulator we
have:
⎥
⎦
⎤
⎢
⎣
⎡
=
T
5
0
T
4
0
r
ˆ
r
ˆ
A
(2)
⎥
⎦
⎤
⎢
⎣
⎡
=
5
T
35
T
1
4
T
24
T
1
r
ˆ
r
ˆ
0r
ˆ
r
ˆ
0r
ˆ
r
ˆ
r
ˆ
r
ˆ
B
(3)
The symbol ^ on a vectorial term of these
equations designates unit vector. In matrices (2) and
(3) the unit vectors correspond to the position
vectors associated with manipulator’s links, as
shown in Figure 3.
The velocity of point C (end-effector) of the
manipulator relative to the table is obtained from
Equation 1 as
•
−
= ρBAt
1
(4)
On the other hand, since the assisted manipulator
can be considered as a redundant one, the general
solution of the inverse kinematic problem is written
as follows:
zJ)J(ItJρ
++
•
−+=
, (5)
where:
BAJ
1−
=
(6)
In Equation (5),
J
+
is the pseudo inverse matrix
of
J, z is an arbitrary vector
3
R
∈
, and I is the unit
matrix
33
R
x
∈
. The term
tJ
+
is the least norm
solution of the inverse kinematic problem which
provides the least norm vector
•
ρ
that allows the
end-effector to satisfy the specified velocity
t. The
expression
(I J J)−
+
z
, is the homogenous solution,
which represents the projection of z on the null
space of
J; it is a joint velocity vector which
produces only internal motion of the manipulator in
direction of z. This internal motion could be used to
improve the kinetostatic performances as much as
possible. To do that, the vector z may be defined as
follows:
)H(kz ρ∇
=
, (7)
where:
)H( ρ
∇
is the gradient of the kinetostatic index
of performance to be optimized.
k is a scale factor of the vector
)H( ρ∇
; it
is defined positive if the index
)H(ρ
must be maximized, or negative if this
one will be minimized.
To improve the accuracy of the manipulator as
much as possible the term
)H(ρ
will be defined as
the condition number of the Jacobian matrix
J. In
addition, the minimization of such index allows
preserving the manipulator’s configurations as far as
possible from singularities of
A and B. If such
singularities arise then the velocity of the end-
effector cannot be controlled. Parallel or serial
singularities of the manipulator may occur if
A or B,
respectively, are not full-rank matrices. More details
on the condition number are given in Section 4.
(c)
A
C
A
B
B
C
(a) (b)
C
A, B
Figure 4: Parallel (a, b) and serial (c) singularities o
f
the manipulator.
1'
4
r
4
r
1'
4
r
5
r
1'
4
r
3
r
1'
4
r
2
r
φ
r
1
r
C
A
C
B
Figure 3: Vectors associated to the manipulator's links.
ICINCO 2006 - ROBOTICS AND AUTOMATION
518

3.2 Singular Configurations
It can be shown that matrix A is singular when
vectors
r
4
and r
5
(i.e. links AC and BC) are parallels;
in such case the manipulator is on a parallel
singularity. On the other hand, in Equation 3 it can
be observed that matrix
B losses its full rank when
r
2
and r
4
, or r
3
and r
5
, become orthogonal and the
manipulator verifies a serial singularity. These
conditions are satisfied by the singular
configurations shown in Figure 4. In cases (a) and
(b) of this Figure, which correspond to parallel
singularities, we observe that not any component of
force being perpendicular to the links AC and BC
can be supported by the point C of the manipulator;
consequently such point could move, even if the
actuators are braked. On the other hand, in case (c),
when the manipulator is on a serial singularity, the
point C cannot be displaced by the manipulator.
Clearly, the aforementioned difficulties to control
the manipulator, associated with both categories of
singularities, are not desirables during the
completion of a task and they should be avoided.
It can also be noted on the one hand that
r
1
has
no influence on matrix A; and on the other hand,
such a vector cannot produce a reduction of the rank
of
B.
4 KINETOSTATIC INDEX OF
PERFORMANCE
The behavior of the Condition Number of the
Jacobian matrix for the assisted manipulator is
examined in this Section. This index has been
largely applied in both parallel and serial
manipulators (i.e. Angeles and Lopez-Cajun, 1992;
Majou et. al., 2002); it bounds the error propagation
from the joint velocities to the operational velocities.
Consequently, it should be minimized in order to
preserve a suitable accuracy of velocity and applied
force of the end effector.
For the assisted manipulator, we analyze the
condition number of
J=A
-1
B, which can be
obtained from:
m
M
λ
λ
κ
=(J)
, (8)
where
M
λ
and
m
λ
are, respectively, the maximum
and the minimum singular values of
J. When κ(J)
becomes one, then the Jacobian matrix is qualified
as isotropic, and the manipulator achieves an ideal
configuration since its accuracy is the best.
On the other hand, the condition number becomes
infinity on singular configurations. The ideal value
of κ(
J) can be obtained by the optimal configuration
only if the design of the manipulator is isotropic
(Angeles and Lopez-Cajun, 1992).
5 TRAJECTORY PLANNING
The trajectory planning problem as considered here
is established as follows: given a main task for the
assisted manipulator specified by a desired
trajectory of the end-effector referred to the mobile
platform, to obtain the joint trajectories in such a
way that the manipulator’s configurations define
values of the condition number of
J as small as
possible during the execution of the task.
It is assumed that the task is specified in a
discrete way by a sufficiently large sample of points
of the desired trajectory. Thus, the process of
solution can be carried out in the following steps for
each path-point:
i) For the point p
i
of the desired path, propose an
arbitrary value of the first joint variable ρ
1i
which
is a member of the admissible domain of
configurations.
ii) For the current point p
i
of the path, solve the
inverse problem of position to find the values of
ρ
2i
and ρ
3i
corresponding to the proposed value
of ρ
1i
. Note that the pose obtained in this step is
completely arbitrary. This one, however, will be
successively improved as described in the next
step.
iii) Find the optimum pose
ρ
i
which satisfies the
current path point p
i
and minimizes the condition
number of the jacobian matrix. In order to do
that, in an internal process of this step,
successively optimal vectors of joint velocities
z’
i
in the null space of the jacobian matrix must
be obtained which allows sequentially improve
the manipulator’s configuration (starting with
that obtained in step ii ) satisfying the current
point p
i
until obtaining of the optimal pose ρ
i opt
.
An optimal vector z’
i
is such that the decreasing
rate of κ
i
(J
i
) is as large as possible. For each
optimal vector z’
i
found in the internal process,
an improved pose is computed by
tΔ+=
•
hi
ii
' ρρρ
, (9)
where
Δ
t
is an arbitrary small time interval, and
hi
•
ρ
is computed by applying the projection of the
GLOBAL OPTIMIZATION OF PERFORMANCE OF A 2PRR PARALLEL MANIPULATOR FOR COOPERATIVE
TASKS
519

optimal vector z’
i
on the null space of J as
follows:
i
hi
z')JJ(Iρ
ii
+
•
−=
(10)
Note that vectors obtained in the internal process
are equivalent to the gradient of the condition
number κ(
J).
When the optimal configuration has been
determined for the actual point p
i
, then the user
changes to the next path-point until arriving at the
last one.
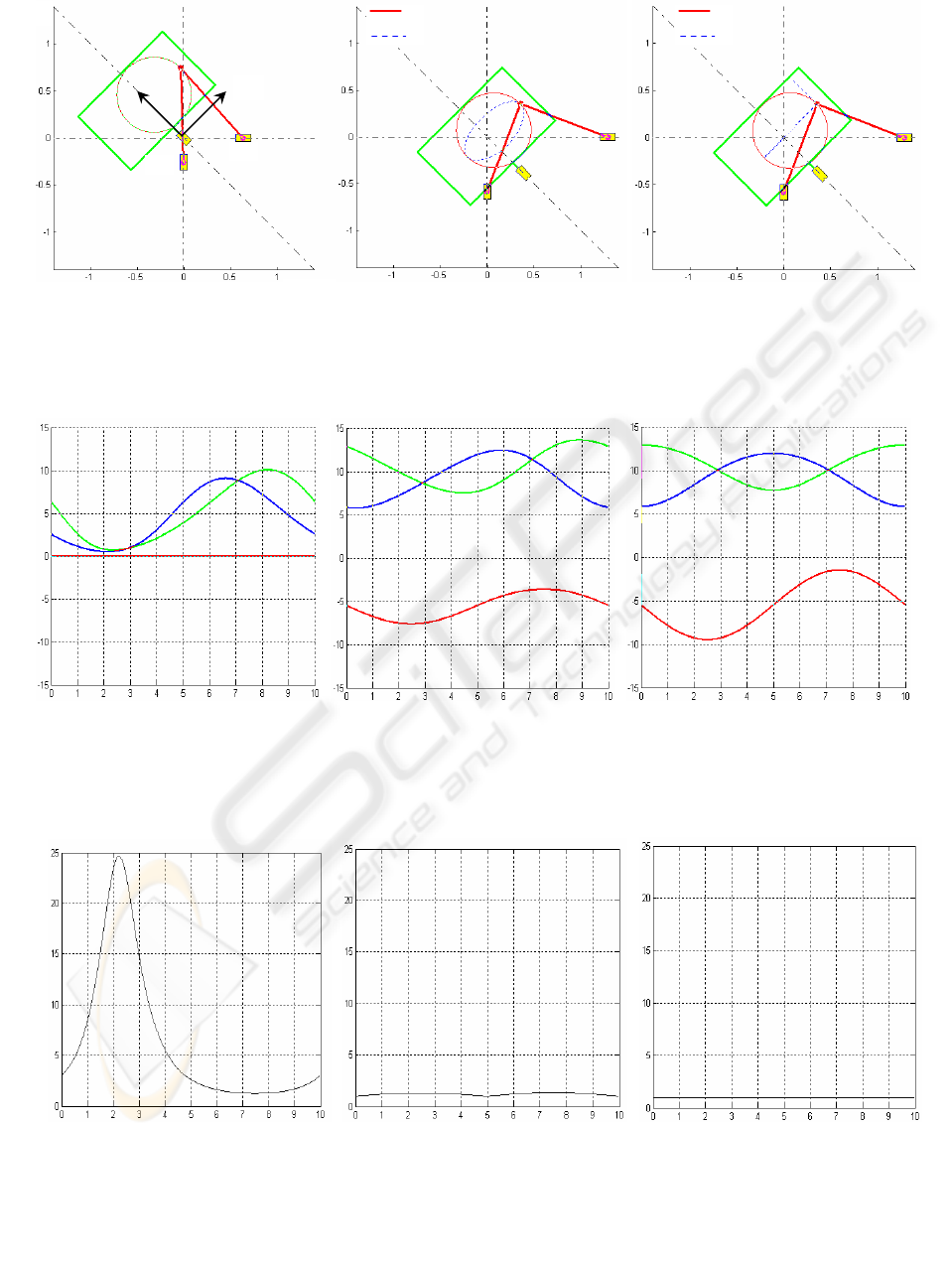
6 CASES OF STUDY
We apply the proposed procedure to the trajectory
planning of the assisted manipulator for a circular
path to be followed by the end-effector for a period
of 10 seconds. The objective of the trajectory
planning consists in the global minimization of the
condition number of the Jacobian matrix during the
execution of the desired task. In order to evaluate the
usefulness of our method, for the same task we study
first the behavior of the condition number in two
additional cases: (a) without motion of the
cooperative platform; and (b) using only the least
norm solution of the inverse kinematic problem.
The diameter of the circular path is 0.8 m and the
coordinates of the center are x=0.1 m and y=0.55 m
relative to the frame attached to the platform. The
software for computations to solve the problem was
developed in Matlab
©
. The algorithm proposed in
Section 5 for optimization of the index of
performance was applied only for the case (c).
Figures 5, 6 and 7 show the initial poses used by
the assisted manipulator for each case. The path
followed by the point C on both the mobile platform
and the fixed frame when the manipulator carries out
its task are also illustrated in these figures. The
obtained joint trajectories are shown in figures 8, 9
and 10, and the behaviors of the condition number
for the three cases are shown in figures 11, 12 and
13.
The expected benefits concerning the kinetostatic
performance of the 2 dof Orthoglide with the
cooperative platform were demonstrated. In the case
of the fixed platform, it can be observed that poor
values of κ(
J) were obtained from 0.5 to 4 sec. The
manipulator is near to singularities when time is
around of 2.2 sec. An improvement of the index was
observed after 4 sec.
Interesting improvements of the manipulator’s
index of performance were observed by
incorporating the cooperative table. Better results
were obtained in the case of the global optimization.
7 CONCLUSION
The performance of a parallel 2 dof manipulator
assisted by a mobile platform was studied in this
paper. The mobile platform was incorporated in the
workstation of the parallel manipulator in order to
increase the manipulator’s workspace and to aid in
improving the performances of the manipulator.
Then an approach was proposed for the global
optimization of the performance of the assisted
parallel manipulator. In fact, our approach allows the
coordination of motion of both the parallel
manipulator and the mobile platform in such a way
that an efficient control was obtained on the
condition number of the jacobian matrix. Thus, a
high level of accuracy of the manipulator can be
preserved during the achievement of the desired
task. The proposed approach is an extension of a
previous method applied to non-cooperative parallel
robots (Alba et al., 2004).
The efficiency of our approach was shown by
applying it to a case of study. The global
optimization of the condition number for the assisted
manipulator was obtained during the execution of a
circular path: only isotropic poses were determined
to achieve the task.
The level of performance obtained by using our
method was compared to that attained in two
supplementary cases of the manipulator: without
mobile platform (Case a), and with platform by
using only the least norm solution of the assisted
manipulator (Case b). The cases b and c have shown
the advantages that can be obtained by using a
collaborative device with a parallel manipulator. A
poor behavior of the condition number was obtained
in Case (a). On the other hand, in Case (b) an
adequate behavior of the index was established:
values near to one were obtained for the complete
path. Nevertheless the more effective control on the
behavior on the index was obtained by applying our
approach.
Even if the least norm solution gave satisfactory
results for the considered path, some difficulties
could be found in paths having other geometries and
the risk of configuration degeneration could arise.
Our approach was developed for the 2 dof
Orthoglide and a 1P cooperative platform; however
ICINCO 2006 - ROBOTICS AND AUTOMATION
520
2
ρ
3
ρ
A
x
0
y
0
B
C
Figure 5: Initial configuration and path
followed without cooperative platform.
Figure 6: Initial (optimal) configuration
and path followed by using the Least
N
orm Solution.
Figure 7: Initial (optimal) configuration,
and path followed by applying Global
Minimization of κ(J).
Trajectory on the mobile platform
Trajectory on the fixed platform
(m)
(m)
(m) (m)
(m) (m)
Trajectory on the mobile platform
Trajectory on the fixed platform
Figure 8: Joint trajectories without
cooperative platform.
t (seg)
t (seg)
t (seg)
ρ
(
d
m
)
ρ
2
ρ
1
ρ
3
ρ
1
ρ
1
ρ
2
ρ
2
ρ
3
ρ
3
ρ
(
d
m
)
ρ
(
d
m
)
Figure 9: Joint trajectories by using
Least Norm Solution.
Figure 10: Joint trajectories
b
y using
Global Minimization of κ(J).
Figure 11: Behavior of κ(J) without
cooperative platform.
t (seg)
κ(J)
Figure 12: Behavior of κ(J) by using
Least Norm Solution.
t (seg)
κ(J)
Figure 13: Behavior of κ(J) by using
Global Minimization of
κ(J).
t (seg)
GLOBAL OPTIMIZATION OF PERFORMANCE OF A 2PRR PARALLEL MANIPULATOR FOR COOPERATIVE
TASKS
521

it could be extended for assisted parallel
manipulators having different architectures. Notice
that, depending on the architecture, unit mismatch
could arise in the Jacobian matrix. In such a case,
this matrix must be homogenized by using a
characteristic length (Daniali et. al., 1995, Alba-
Gomez et al, 2005).
ACKNOWLEDGEMENTS
This work is a part of a project of LAFMAA, which
is supported by CNRS and CONACYT.
REFERENCES
Alba G. O., Pámanes G. J. A., Wenger P. Optimación
Global del Desempeño de Manipuladores Paralelos
Redundantes en la Ejecución de Trayectorias
Especificadas;
Proceedings of the 2004 Mexican
Congress of Robotics
, pp. 45-50; Torreón, México,
2004.
Alba G. O., Pámanes G. J. A., Wenger P. Consistent
kinetostatic indices for planar 3-DOF parallel
manipulators: application to the optimal kinematic
inversion;
Proceedings of the 2005 ASME
International Design Engineering Technical
Conference & Computer and Information in
Engineering Conference
; paper DETC 2005-84326,
2005.
Angeles J. , López-Cajún C. 1992. Kinematic
Isotropy and Conditioning Index of Serial Robotic
Manipulators; Int. J. Robotics Research; 11 (6), pp.
560-571.
Daniali H., Zsombor-Murray P, Angeles J. The isotropic
design of two general classes of parallel manipulators;
Journal of Robotics Systems, Vol. 12, No. 12, pp 785-
805, 1995.
Gosselin C., Angeles J., 1990. Singularity analysis of
closed-loop kinematic chains.
Proceedings of the 1990
IEEE International Conference of Robotics and
Automation
.
Hemmerle J.S., Prinz F.B., 1991. Optimal Path
Placement for Kinematically Redundant Manipulators.
Proceedings of the 1991 IEEE International
Conference of Robotics and Automation
; pp.1234-
1243.
Majou F., Wenger P., Chablat D., 2002. Design of 2-DOF
Parallel Mechanisms for Machining Applications.
Advances in Robot Kinematics: Theory and
Applications
; Kluwer Academic Publishers. Edited by
J. Lenarcic and F. Thomas; pp. 319-328.
Moreno A. H., Modelado y Planificación de Trayectorias
de Robots Paralelos: Estudio de Tres Casos.
Thesis of
Master in Sciences.
Instituto Tecnológico de la
Laguna, 2006.
Wenger P., Gosselin C., Chablat D., 2001. A comparative
study of parallel kinematic architectures for machining
applications; 2
nd
Workshop on Computational
Kinematics, Seoul South Korea.
ICINCO 2006 - ROBOTICS AND AUTOMATION
522
