
DESIGN OF MAX-PLUS CONTROL LAWS TO MEET
TEMPORAL CONSTRAINTS IN TIMED EVENT GRAPHS
Saïd Amari, Jean Jacques Loiseau, Claude Martinez
IRCCyN, UMR CNRS 6597, 1 rue de la Noë 44321 Nantes, France
Isabel Demongodin
LISA, 62 av. Notre Dame du Lac 49000 Angers, France
Keywords: Timed Event graph, Max-Plus algebra, Temporal constraints, Control.
Abstract: The aim of the work presented is the control of timed event graph in order to meet tight temporal
constraints. The temporal constraint represents the maximal duration of a chemical or thermal treatment, for
instance. We formulate the problem in terms of control of linear Max-Plus models. A method for the
synthesis of a control law ensuring the meeting of constraints is first described for a single input single
constraint. Then, the single input multi constraint problem is tackled and finally, the method is extended to
the multi inputs, multi constraints problem. The proposed method is illustrated on an example.
1 INTRODUCTION
We consider in the sequel a class of deterministic
controlled processes subject to strict time
constraints. Such time critical systems are frequent
in the industry, for instance in the case of a thermal
or chemical treatment, in the car industry for the
rubber parts, in the semiconductor industry and also
in the food industry. Of course the question is to
validate some temporal conditions (see for instance
(Berthomieu and al., 1991), (Ghezzi and al., 1991),
(Bonhomme and al., 2001), (Cofer and Garg, 1995)).
In the present contribution, we formulate this
problem in terms of a control problem, assuming
that some inputs of the process can be controlled (it
is generally the case). We propose a method to solve
the inverse problem, synthesizing a control law so
that the temporal constraint is validated. We use the
formalism of timed event graph, and their algebraic
models which are linear over dioids (Baccelli and
al., 1992).
The timed event graph behavior is modeled with
Max-Plus equations, and the temporal constraints
meeting problem is represented with inequalities,
also in the so-called Max-Plus algebra. The control
approach that we propose is quite different from that
considered within the so-called supervisory control
framework ((Holloway and al., 1997), (Moody and
al., 1996)). Here the time is explicitly taken into
account. Timed event graphs and dioids formalism
has been used by ((Lahaye et al., 2004), (Atto et al.,
2006)) to treat slightly different timed constraint
problems. In (Lahaye et al., 2004), the question is
formulated as a model matching problem and the
temporal constraint appeared as an additional
requirement. (Atto et al., 2006) are interested to
particular temporal constraints and they suppose that
the places subjected to these constraints are initial
marking null. Our work also differs from the
existing literature on the control of (timed) discrete
event systems, since the control laws we consider
may involve some delays.
In the present paper, we propose a method for the
synthesis of control law that permits to meet a given
set of time constraints. The resulting control law
itself is finally defined a Max-Plus linear difference
equation, involving a finite number of delays. Such
an equation corresponds to feedback that is also a
timed event graph. A first approach of control for
timed event graph under strict temporal constraints
was presented in (Amari and al., 2005). This
approach has been developed in the Min-Plus
algebra, under the hypothesis that all temporizations
of the considered graph are integers. In this present
contribution, this condition is not required, we
91
Amari S., Jacques Loiseau J., Martinez C. and Demongodin I. (2006).
DESIGN OF MAX-PLUS CONTROL LAWS TO MEET TEMPORAL CONSTRAINTS IN TIMED EVENT GRAPHS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 91-98
DOI: 10.5220/0001214700910098
Copyright
c
SciTePress

consider a timed event graph with temporizations
that may be real numbers.
The paper is organized as follows. In Section 2,
some backgrounds are recalled, featuring some
notations concerning the Max-Plus semiring, the
timed event graphs and their Max-Plus linear
models, the concept of a state equation. The
problem, of finding a causal control verifying
critical time constraints, is formulated in Section 3.
We propose in Section 4 a procedure for the control
synthesis, considering first the case of a single input
system with a single temporal constraint. Two
conditions are proposed, which are sufficient for
ensuring the existence of a solution. A simpler
condition, which is satisfied in many practical cases,
and is simpler to check, is also provided. Then we
extend the method to the case of many different
constraints. The multivariable case is examined in
Section 5 and Section 6 is devoted to illustrative
example. Finally Section 7 is devoted to the
conclusion.
2 BACKGROUNDS
2.1 Max-Plus Algebra
A monoid is a set, say
D , endowed with an internal
law, noted
⊕
, which is associative and has a neutral
element, denoted
ε , ,.aDa a aεε∀∈ ⊕=⊕ = A
semiring is a commutative monoid endowed with a
second internal law, denoted
⊗ , which is
associative, distributive with respect to the first law
⊕
, has a neutral element, denoted e , and admits ε
as absorbing element:
,.aDa aεε ε∀∈ ⊗=⊗ =
A dioid is a semiring with an idempotent addition:
,.aDaa a∀∈ ⊕ = The dioid is called commutative
if the second law
⊗ is commutative.
We shall consider in the sequel the so-called Max-
Plus algebra that is
{
}
{
}
(,max,)∪−∞∪+∞ +\
. The
Max–Plus algebra, denoted
max
\ is a commutative
dioid, the law
⊕ is the operation max, having the
neutral element
ε
=−∞ and the second law
⊗
is
the usual addition, with neutral element
0e =
.
If
n ∈ ` and
max
,
n
vw∈ \ , we denote vw⊕ the
vector with components
max( , )
ii ii
vw vw⊕= for
1i = to n. If no confusion can arise, when ,pq
∈
` ,
max
p
n
A
×
∈ \ and
max
nq
B
×
∈ \ are given matrices,
A
B⊗
(or just
.
A
B ) will denote the matrix multiplication
in
max
\
, defined by the following expression:
1
(.) ( ) max( ).
n
ij ik kj ik kj
k
k
A
BAB AB
=
=⊕ ⊗ = +
The Kleene star of a square matrix
max
nn
M
×
∈ \ ,
denoted
M
∗
is defined by
i
i
M
M
∗
∈
=⊕
`
, where
0
M
equals the unit matrix, which entries equal
e on the
diagonal, and
ε elsewhere. Let us recall that
max
n
v ∈ \ then
.
x
Mv
∗
=
is the maximal solution of
both the inequality,
.
x
Mx v≥⊕
,
and the equality,
.
x
Mx v=⊕, (Baccelli and al., 1992).
2.2 Timed Event Graphs, Linear
Max-Plus Models
An event graph is an ordinary Petri net where each
place has exactly one upstream transition and one
downstream transition. A timed event graph is
obtained by associating delays to the places or to
transitions of an event graph. In our case, the delays
are associated to places. We note n the number of
transitions having at least one upstream place, and
m
stands for the number of source transitions, noted
tu, having no upstream place. The unique place
relying
j
t to
i
t is denoted
ij
p , if any, the
corresponding delay is denoted
ij
τ
and its marking
is denoted
ij
m .
A transition
j
t is controllable, if there exist a path,
denoted
α
, from transition tu to transition
j
t . This
path
is a sequence of transitions and places, of the
form
11 12 2
( , , , , ,..., )
uk k k k k j
tu p t p t t
. We denote m
α
the
sum of marking along the path
α
,
kl
kl
kl kl
p
p
mmm
α
α
α
∈
∈
=⊗ =
∑
.
To represent the dynamic of the timed event graph in
Max-Plus algebra, we associate to each transition a
firing time for the
k
th
occurrence. We note ()
s
uk,
for source transitions
s
tu and ()
i
k
θ
for other
transitions
i
t .
Example:
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
92

Figure 1: Example.
The timed event graph for the Figure 1, leads to the
following equation:
3 31 1 31 32 2 32
( ) max( ( ), ( )),kukmukmθτ τ=+−+−
which, in Max-Plus algebra appears to be linear:
3 31 1 31 32 2 32
() ( ) ( ).kukm ukmθτ τ=⊗ − ⊕⊗ −
,
In general, the dynamical behavior of a timed event
graph can be expressed by means of a linear
equation in Max-Plus algebra, as follow,
0
( ) ( . ( ) . ( )),
mm
m
k A km Bukm
θθ
≥
=⊕ − ⊕ − (1)
where the components of the vector
()k
θ
are the
firing times of the
n transitions t
i
, the components of
u(k) is the firing dates of the source transitions tu.
The matrix
m
A
that belongs to dioid
max
nn
×
\ , is a
matrix which entry
,mij
A
equals to
ij
τ , the delay
associated to place
ij
p , if this place exists and the
associated delay is
ij
τ
, and
ε
else. Similarly, the
entries of matrices
max
nm
m
B
×
∈ \
correspond to the
delays of the places following source transitions.
Equation (1) is implicit in general. It is worth
replacing it by the following explicit equation,
00
0
() ( . .( ) . .( ))
mm
m
kAAkmABukm
θθ
∗∗
>
=⊕ − ⊕ −
, (2)
where
0
A
∗
is the Kleene star of
0
A
, defined in the
previous section. (See (Baccelli and al., 1992)).
Analogously to the case of usual linear systems, the
explicit equation 2 can be brought in state space
form. In order to obtain a state space model, one first
expands all the places with marking
1m > into
m
places with marking equal to 1. Hence one adds
(1)m − intermediate transitions. One has then the
resulting extended state vector
()
x
k , which belongs
to
max
N
\
, with 'Nnn
=
+ and n’ is the number of
added intermediate transitions.
The dynamic behavior of the expanded timed event
graph is then described by an equation of the form
01
ˆˆ
ˆ
() .() .( 1) .()
x
kAxkAxk Buk=⊕−⊕,
which can be rewritten into the following explicit
form, where
01
ˆˆ
.
A
AA
∗
= and
0
ˆ
ˆ
.
BAB
∗
= ,
() .( 1) .()
x
kAxk Buk
=
−⊕ . (3)
All these formulations permit to point out that the
behaviour of a controlled timed event graph is
deterministic, depending on the input
()uk and on
some initial conditions. This dependence can be
explicated, and we shall make use of the following
formulation:
1
'
'0
() .( ) . .( ')
k
k
x
kAxk ABukk
ϕ
ϕ
ϕ
−
=
⎡
⎤
=−⊕⊕ −
⎢
⎥
⎣
⎦
, (4)
which holds true, for each integer
1
ϕ
≥ .
In the following, we shall assume that the input
u(k)
is actually a control, which can be arbitrarily
assigned. For instance in a production process, the
input corresponds to the authorization of performing
a certain operation. Typically the beginning of a task
performed by a robot, for instance, is subject to such
a control input.
3 PROBLEM OF TEMPORAL
CONSTRAINTS
Strict time constraints are frequent in flexible
manufacturing system (Amari and al., 2004) and
semiconductor manufacturing (Kim and al., 2003).
One can for instance consider the example of a
production process with a furnace for realizing a
thermal treatment. The duration of any treatment in
the furnace is fixed, or defined by a time interval.
One wants to control the system to respect this
constraint.
The definition of a timed event graph already takes
into account a delay on each place that corresponds
to a minimal holding time. The maximal duration
appears as an additional constraint that the system
should meet. Rather than a verification problem, we
formulate the question as a control problem.
t
3
tu
2
m
32
m
31
31
τ
32
τ
tu
1
DESIGN OF MAX-PLUS CONTROL LAWS TO MEET TEMPORAL CONSTRAINTS IN TIMED EVENT GRAPHS
93
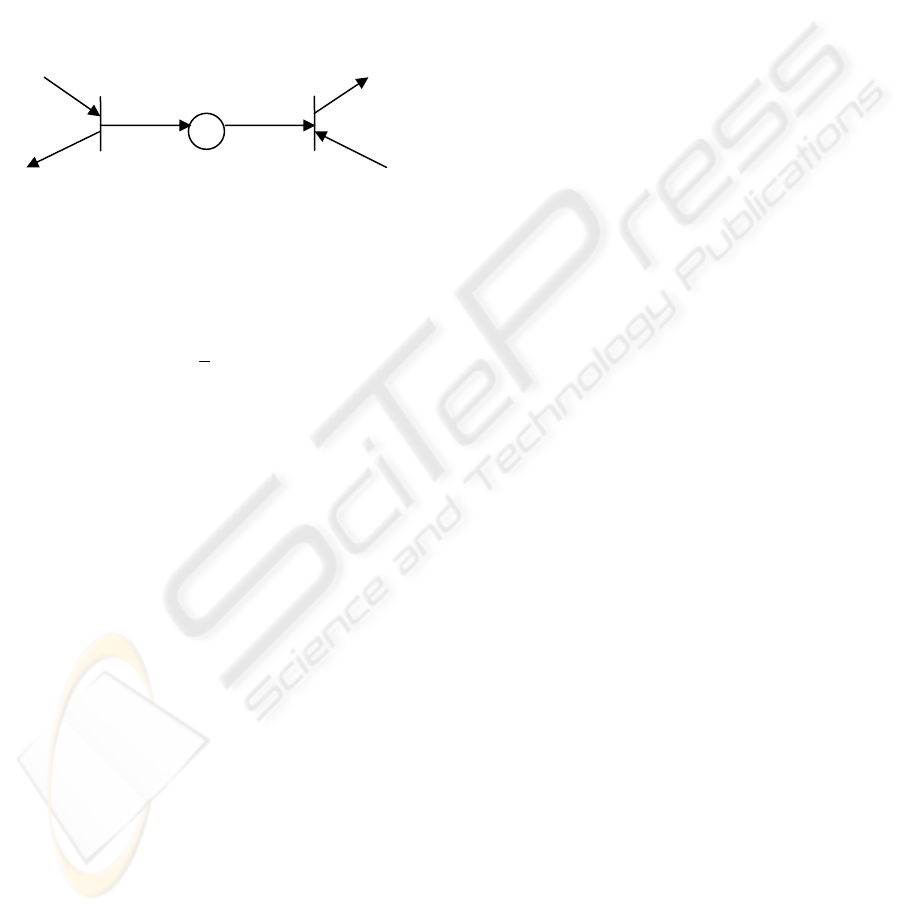
3.1 Temporal Constraint
In general, the sojourn time of the tokens in place
ij
p
can be higher or equal to
ij
τ
. In our case, one
imposes a maximum sojourn time, noted
max
ij
τ
.
Hence
ij
p
is a place subject to a strict time
constraint, an interval of time
,
max
ij ij
ττ
⎡⎤
⎣⎦
is
associated to the place
ij
p
. See Figure 2.
Figure 2: Temporal constraint.
This additional temporal constraint is expressed
through the following inequality:
max
() . ( ),
iijjij
x
kxkm
τ
≤− (5)
where the product is over
max
\ .
3.2 Causal Feedback
We consider a process modelled by (3), subject to
the additional constraint (5). We want to determine a
control
()uk that satisfies the constraint (5) for
0k > . We shall a priori research this control in the
form of a well posed causal feedback of the form,
() .( 1)uk Fxk=−, with 1k > .
Remark 1:
Let us note that a static control law
() .()uk Gxk= could lead to implicit loops. For
example, given a system with state equation
() ()
x
kuk= (() .( 1) .()
x
kAxk Buk=−⊕ , with
A
ε
= and Be= ), the control law equation would
be
() ()uk xk= . On one hand, a badly posed
feedback may appear using
() .()uk Gxk= , and the
other hand a feedback of the form
() .( 1)uk Fxk=−
is always well posed, leading to the closed loop
() ( . ).( 1)xk A BF xk=⊕ −. Furthermore, given a
system
() .( 1) .()
x
kAxk Buk=−⊕ , one can always
build a well posed feedback of the form
() .()uk Gxk
=
, with (.(.).)
F
GBG A
∗
= . Therefore, it
is not restrictive to suppose that the feedback is of
the form
() .( 1)uk Fxk
=
− , with
(.(.).)
F
GBG A
∗
=
.
4 SINGLE CONTROL
4.1 Single Constraint
We have in this case a timed event graph modelled
by the linear Max-Plus equation (3) and subject to a
single temporal constraint (5). We propose a method
for the synthesis of a control law solving the
problem of temporal constraint, provided that the
following additional hypothesis is satisfied.
We suppose that the transition
j
t is controllable, i.e.
there exists a path
α
from tu to
j
t . One note m
α
the cumulated markings along this path.
The j
th
component ()
j
x
k satisfies (6):
(.).( ) ()
m
jj
A
Bukm xk
α
α
−≤ (6)
Inequality (6) translate the relation between
tu and
j
t
.
According to equation (4), the i
th
component of the
vector
()
x
k is given by the following explicit
expression:
1
'
1'0
() ( ). ( ) ( .).( ')
N
k
iirr i
rk
x
kAxk ABukk
ϕ
ϕ
ϕ
−
==
⎡⎤
⎢⎥
=⊕ − ⊕ ⊕ −
⎢⎥
⎣⎦
(7)
for every integer
1ϕ ≥
.
Taking (7) into account, it appears that the constraint
(5) is satisfied if the two following inequalities hold,
max
1
().( ) .( )
N
ir r ij j ij
r
A
xk xk m
ϕ
ϕτ
=
⊕−≤−, (8)
1
'max
'0
(.).( ') .( )
k
iijjij
k
A
Buk k xk m
ϕ
τ
−
=
⊕−≤−. (9)
Further, taking (6) into account, we have
max
1
().( ) .( .).( )
ij
N
m
ir r j ij
r
A
xk A B uk m m
α
ϕ
α
ϕτ
=
⊕−≤ −− (10)
1
'max
'0
(.).( ') .( .).( )
ij
m
k
ijij
k
A
Buk k A B uk m m
α
ϕ
α
τ
−
=
⊕−≤ −−
(11)
max
,
ij ij
ττ
⎡⎤
⎣⎦
t
i
t
j
m
ij
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
94

If inequalities (10) and (11) hold, then (8) and (9)
are satisfied. Condition (10) holds true for all
controls:
max
1
( ) (( ) ( . ) ). ( 1)
ij
N
m
ir j r
r
uk A A B x k
α
ϕ
τ
=
≥⊕ − − − ,
with
(1)
ij
mm
α
ϕ =++. If condition (12) holds for
all
()
ir
A
ϕ
ε≠ , therefore the former expression
define suitable causal control laws u(k).
max
() .( .)
ij
m
ir j
A
AB
α
ϕ
τ≥ , (12)
with
1r = to N . Inequality (11) is satisfied if the
inequalities (13) and (14) are respected.
'max
(.) .( .)
ij
m
k
ij
A
BAB
α
τ≤ , (13)
(')( )
ij
uk k uk m m
α
−≤ −− , (14)
with
'0k = to 1ϕ − .
Inequality (13) is a condition which depends on
temporizations of the considered timed event graph.
As the function
()uk is non decreasing, then
inequality (14) is checked if and only if the
following inequality is satisfied:
for ' 0k
= to
1ϕ −
, '
ij
kmm
α
≤+.
This last inequality is true for
(0).
ij
mm
α
==
The conditions (12), (13) and the hypothesis
(0)
ij
mm
α
== are sufficient to ensure the existence
of feedbacks which guarantee the meeting of the
temporal constraint.
Theorem 1:
The control laws defined by the inequality:
max
1
() ( ). ( 1),
ij
N
ir j r
r
uk A B x kτ
=
⎡⎤
≥⊕ − − −
⎢⎥
⎣⎦
guarantee the meeting of the temporal constraint (5)
if the hypothesis ( 0)
ij
mm
α
== holds and if
conditions (12) and (13) are satisfied.
Proof:
Previously, we saw that the two inequalities (10) and
(11) imply the temporal constraint (5). As specified
in Theorem 1, the condition (12) is satisfied, and
then feedback given as in the theorem ensures the
respect of the condition (10). We have the
hypothesis
(0)
ij
mm
α
== and 1ϕ = , then the
inequality (11) is written as follows:
max
.() . .()
ij
ij
Buk B ukτ≤
This last inequality is equivalent to (13) which is
checked by hypothesis.
,
4.2 Multiple Constraints
We consider now the case of a timed event graph,
having one source transition which is a control, but
Z
places are constrained, noted
z
p
, for
1z =
to
Z
. For each constrained place
z
p
, let
z
m
,
z
τ
and
max
z
τ
respectively denote the initial marking, the
minimal and maximal delays. Further, let
z
t and
'
z
t
respectively denote the input and output transitions
of the place,
()
z
x
k and
'
()
z
x
k denote the
corresponding firing dates, and
z
m
α
denote the
cumulated marking along a path
z
α
going from the
source transition
tu
to
z
t . These added temporal
constraints are expressed by the inequalities:
max
'
() . ( )
z
zz z
x
kxkmτ≤− (15)
for
1z =
to
Z
.
We denote
()
z
uk the control law calculated as in the
previous section to satisfy the z
th
temporal constraint.
The following Theorem defines a causal feedback
which ensures the respect of all Z temporal
constraints.
Theorem 2:
The equation
1
() (),
Z
z
z
uk u k
=
=⊕
with
max
'
1
() ( ). ( 1)
z
N
zzrzr
r
uk A B xkτ
=
=⊕ − − − ,
defines a causal control which ensures the meeting
of all the temporal constraints (15), if the following
conditions are satisfied: for z=1 to Z,
0
z
z
mm
α
==
,
max
'
.,
z
z
z
BBτ≤
and
max
'
.,
z
z
rz
A
Bτ≥ for r=1 to N.
Proof:
DESIGN OF MAX-PLUS CONTROL LAWS TO MEET TEMPORAL CONSTRAINTS IN TIMED EVENT GRAPHS
95

The conditions quoted in this theorem are sufficient
so that the feedback
()
z
uk satisfies the z
th
temporal
constraint. The following inequality:
1
() (),
Z
zz
z
uk uk
=
⊕≥
is true for z=1 to Z.
It is finally clear that
1
() ()
Z
zz
uk u k
=
=⊕ validates all
the Z temporal constraints.
,
5 MULTIVARIABLE CONTROL
In this section, a considered timed event graph
contains m source transitions, with
1m ≥ . Its
dynamical behaviour is represented by a linear
Max-Plus system (3). The control law is a vector of
m components. Firstly, we suppose that
ij
p is the
single place subjected to an additional temporal
constraint (5). We calculate a vector
max
()
m
uk ∈ \ ,
with
1m ≥ , which is a control law that must satisfy
the constraint (5). The components of
()uk are
noted
(),
s
uk for 1s = to m . We note by
s
m
α
, the
cumulated markings along a path
s
α
from
s
tu to
j
t .
We suppose that
0
s
ij
mm
α
==
, i.e. the initial
marking of the place
ij
p and along equal zero the
path
s
α
.
This hypothesis is translated by the following
inequality:
.() ().
js s j
Buk xk≤
(16)
Theorem 3:
The meeting of the temporal constraint (5) is
guaranteed if:
(a) There exits
s such that:
max
1
() ( ). ( 1)
N
sirjsijr
r
uk A B xkτ
=
⎡⎤
≥⊕ − − −
⎢⎥
⎣⎦
,
and
()
l
uk ε==−∞ for ls≠ , and
(b) The both following sets of conditions are
satisfied:
(i)
ma x
.
ir ij js
A
B
τ
≥ for r=1 to N and .
ir
A
ε
≠
(ii)
ma x
.
is ij js
B
B
τ
≤ for s=1 to m.
Proof.
Applying (3), the i
th
component of ()
x
k is
11
() . ( 1) . ()
Nm
iirr iss
rs
x
kAxk Buk
==
⎡
⎤⎡ ⎤
=⊕ − ⊕⊕
⎢
⎥⎢ ⎥
⎣
⎦⎣ ⎦
. (17)
Taking (17) into account, it appears that constraint
(5) (with 0
ij
m
=
) is satisfied if both following
conditions hold,
ma x
1
.( 1) .()
N
ir r ij j
r
A
xk xk
τ
=
⊕−≤
and
ma x
1
.() .().
m
is s ij j
s
Bu k x k
τ
=
⊕≤
Futher, taking (16) into account, these conditions
become
ma x
1
.( 1) . .()
N
ir r ij js s
r
A
xk Buk
τ
=
⊕−≤
and
ma x
1
.() . .().
m
is s ij js s
s
Bu k Bu k
τ
=
⊕≤
Conditions (i) and (ii) being verified, and the control
law satisfying the inequality of the Theorem 3, one
can check that the constraint (5) is satisfied.
,
Corollary:
Let a timed event graph with m source transitions
(
1m ≥ ) and Z additional temporal constraints (15).
The causal control law which guarantees the respect
of the
Z
constraints is defined by:
1
() ()
z
Z
s
z
uk u k
=
=⊕ ,
where ( )
z
s
uk is the control law, calculated by
Theorem 3, to check the z
th
constraint.
Proof:
A control law ( )
z
s
uk, validates the z
th
constraint, if
conditions (i) and (ii) of Theorem 3 are satisfied.
Thus, we have, for
1z
=
to Z,
1
() ()
zz
Z
ss
z
uk uk
=
≤⊕ .
According to Theorem 3, it is clear that the control
law
1
() ()
z
s
Z
z
uk u k
=
=⊕ guarantees the respect of all
Z
temporal constraints. ,
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
96

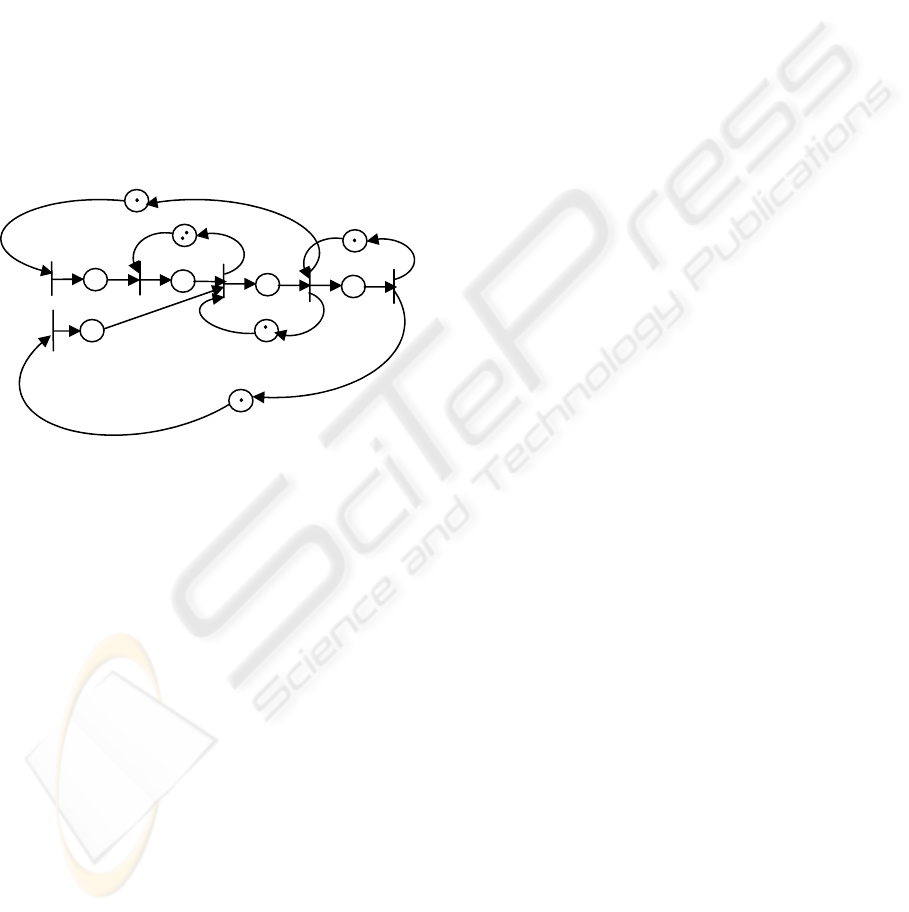
6 EXAMPLE
Consider the timed event graph of Figure 3. This
graph contains two source transitions modelling
respectively, control
1
()uk and control
2
()uk,
(2)m = .
Figure 3: Timed event graph.
Two additional temporal constraints are added to
this graph, and
are expressed respectively by the
following inequalities:
21
() 1. (),
x
kxk≤
32
() 1. ().
x
kxk≤
The problem consists in calculating a control vector,
1
2
()
() ,
()
uk
uk
uk
⎛⎞
=
⎜⎟
⎝⎠
which satisfies these both constraints.
By applying our approach, the previous graph has
been transformed into the graph Figure 4, with
max
1m = . To do so, place
12
p marked to 2 has been
split into two places marked to 1 and the
intermediate transition
5
t is added.
Figure 4: Extended equivalent graph.
The state equation associated with this new timed
event graph is:
11 1
() .( 1) .(),
212 21
545 54
1
ee
e
x
kxkuk
ee
εεεε ε
εε ε
εε
εε
εεε ε
⎛⎞⎛⎞
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎟⎟
⎜⎜
=−⊕
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎟⎟
⎟⎟
⎜⎜
⎟⎟
⎜⎜
⎝⎠⎝⎠
⎟⎟
⎜⎜
where the components of
()
x
k are the firing times
of the transitions
1
t ,
2
t ,
3
t ,
4
t and
5
t , and the vector
()uk is the control law. We shall then apply
Corollary to calculate a control
()uk which
guarantees the meeting of both temporal constraints.
This example, it is enough to find, for each temporal
constraint, only one component of the vector
()uk
to guarantee the meeting of this constraint
.
Firstly, by applying of Theorem 3, we determine a
component of the vector
()uk , which satisfies the
first constraint. We have
max max
21
1
ij
ττ
== and the
initial marking of the place
21
p is
21
0m = . It exist a
path
1
α
from transition
1
tu to transition
1
t and its
initial marking is
1
0m
α
=
. We can check that one
has
ma x ma x
21 11
1
ij js
BB
ττ
+
=+=
, and
2
(11)
ir r
AA
ε
εε
=
= , hence the condition (i) of
Theorem 3 holds. Similarly, we check that
21
1
is
BB
=
= , so that the condition (ii) of Theorem 3
holds too. Thus, the component of
()uk which
guarantees the meeting of the first constraint is
[]
5
12 35
1
() ( 1). ( 1) ( 1) ( 1)
rr
r
uk A xk xk xk
=
=
⊕− −=−⊕−
.
Secondly, we determine also by Theorem 3 a
component of the vector
()uk , which satisfies the
second constraint. In this case, we have,
max max
32
1
ij
ττ
=
=
and the initial marking of the place
32
p is
32
0m
=
. It exist a path
2
α
from transition
2
tu to transition
2
t and its initial marking is
2
0m
α
=
. We can check that one has
ma x ma x
32 22
1
ij js
BB
ττ
+
=+=, and
3
(212)
ir r
AA
ε
ε
== ,
hence the condition (i) of Theorem 3 holds. We
check also that
32
1
is
BB
=
= , so that the condition (ii)
of Theorem 3 holds too. Thus, the component of
()uk which guarantees the respect of the second
constraint is
[]
5
23
1
34 5
() ( 1). ( 1)
1. ( 1) ( 1) 1. ( 1).
rr
r
uk A xk
xk xk xk
=
=⊕ − −
=
−⊕ −⊕ −
t
4
1
tu
1
t
1
t
2
1
t
3
1
1
3
0
tu
2
0
0
0
t
5
tu
1
1
0
t
1
t
2
1
t
3
1
1
3
0
tu
2
0
t
4
DESIGN OF MAX-PLUS CONTROL LAWS TO MEET TEMPORAL CONSTRAINTS IN TIMED EVENT GRAPHS
97
Finally, according to Corollary, the control law
which guarantees the meeting of both temporal
constraints is given by the following vector:
35
34 5
(1) (1)
() .
1. ( 1) ( 1) 1. ( 1)
xk xk
uk
xk xk xk
−⊕ −
⎛⎞
=
⎜⎟
−⊕ −⊕ −
⎝⎠
After comparison between the terms of each
component of the vector, the control law is
simplified to:
3
4
(1)
() .
(1)
xk
uk
xk
−
⎛⎞
=
⎜⎟
−
⎝⎠
This feedback can be interpreted by two places of
control connected to the timed event graph to
guarantee the respect of the temporal constraints.
The controlled graph is given in Figure 5.
Figure 5: Controlled timed event graph.
Remark 2:
The same example was treated with the method
developed in Min-Plus algebra (Amari and al.,
2005). It is worth noting that the synthesis of the
Max-Plus control is easier than that in the Min-Plus
algebra. In this case, there are not necessary
compute of power for the matrix.
7 CONCLUSION
We have developed a method for control synthesis
of timed event graphs subject to strict temporal
constraints. A generalization for timed event graphs
with multivariable control has been proposed in this
paper. This method is illustrated on an example. The
conditions (12) and (13) are shown here to be
sufficient conditions, we are investigating actually
the existence of necessary and sufficient conditions
for the synthesis of control laws which ensure the
meeting of the temporal constraints. We will
continue the comparison of this method with those
developed in (Lahaye et al., 2004) and (Atto and al.,
2006). We hope to apply this method for real
systems, notably for the verification and validation
of automated systems as well as telecommunication
processes and real-time software.
REFERENCES
Amari S., I. Demongodin and J.J. Loiseau, Sizing, cycle
time and plant control using dioid algebra,
Chapter 6
in Supply Chain Optimisation, Series Applied
Optimization, Springer. pp. 71-85, 2004.
Amari S., I. Demongodin and J.J. Loiseau, Control of
Linear Min-Plus Systems under Temporal
Constraints.
44
th
IEEE Conference on Decision and
Control and European Control Conference
, Seville,
2005.
Atto A.M, C. Martinez et S. Amari, Synthèse de
superviseur pour la commande des systèmes à
événements discrets soumis à des contraintes de temps
strictes. Soumis à la revue ARIMA, INRIA, ISSN
1638-5713, 2006.
Baccelli F., G. Cohen, G.J. Olsder, and J.-P. Quadrat,
Synchronization and Linearity:
An algebra for
Discrete Event Systems,
Wiley, 1992.
Berthomieu B. and M. Diaz, Modelling and verification of
time dependant systems using time Petri nets
, IEEE
Transactions on Software Engineering,
Vol. 17, No. 3,
pp. 259-273, 1991.
Bonhomme P., P Aygalin and S. Calvez, Systèmes à
contraintes de temps : Validation, Evaluation et
contrôle
, MSR, Toulouse, 2001.
Cofer D. D., Garg V.K., Control of event separation times
in discrete event systems.
In Proceedings 34th IEEE
Conference on Decision and Control
, pp. 2005 – 2010,
New Orleans, 1995.
Ghezzi C., D. Mandrioli, S. Morasca and M. Pezze, A
unified high-level Petri net formalism for time critical
systems,
IEEE Transactions on Software Engineering,
Vol. 17, No. 2, pp. 160-172, 1991.
Holloway L.E., B.H. Krogh and A. Giua, A survey of Petri
net methods for controlled discrete event systems,
Kluwer Academic Publishers pp.151-190, Boston,
1997.
Kim J.H, T.E Lee and H.Y Lee, Scheduling Analysis of
Time-Constrained Dual-Armed Cluster Tools,
IEEE
Transactions on Semiconductor Manufacturing, vol.
16, no. 3, august 2003.
Lahaye S., B. Cottenceau and A. Correïa, Commande des
graphes d’événements temporisés avec contraintes de
temps critique,
CIFA’04, Tunisie, 2004.
Moody J., K. Yamalidou, M. Lemmon and P. Antsaklis,
Feedback control of Petri nets based on place
invariants,
Automatica, vol 32, pp. 15-28, 1996.
0
t
3
1
1
3
1
t
4
tu
0
0
t
1
t
2
1
tu
0
0
ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
98
