
ACO BASED METHOD COMPARATION APPLIED TO FLEET
MANAGEMENT PROBLEM
M. Antón-Rodríguez
1
, D. Boto-Giralda
2
, F. J. Díaz Pernas
3
, J. F. Díez Higuera
4
Signal Theory, Communications and Telematic Engineering Department, ETSIT,
University of Valladolid, Campus Miguel Delibes, 47011 Valladolid, Spain
Keywords: Route calculation, resource allocation, ACO meta-heuristic, optimization.
Abstract: Road Transport enterprises do have the need of fleet management applications in order to upgrade their
efficiency; the fulfilment of that need takes us in the search of optimization algorithms whose performance
better suits not only the optimal route search problem, but the resource allocation too. ACO (Ant Colony
Optimization) meta-heuristic has proven to be very useful when solving similar problems, but as ACO
comes in several different flavours, to make the right algorithm choice is the first step in the search for a
solution. This document presents a performance study made upon several ACO algorithms over the fleet
management problem, with the objective of determining which one is the best finding the optimal solution
in a reasonable amount of time.
1 INTRODUCTION
The heavy overburden suffered by the road networks
of almost all first world countries makes daily
mobility to be strongly restricted. Those restrictions
are quite stressed when other adverse conditions
concur. Conditions like bad weather, accidents or
road works add higher levels of inconvenience.
Those facts affect transport enterprises deeply,
downgrading their quality of service and increasing
costs. This is a reason why road transport fleet
management applications, capable of finding the
best possible route and assigning each freight to the
right vehicle of the fleet can be a key resource for
this kind of companies, helping them to minimize
costs and to upgrade the safety of their employees
and the quality of the services offered to their
clients.
Both the route calculation and the resource
assignment are very good NP-hard problem samples;
as such, the number of possible solutions grows
exponentially with the problem's dimensions. These
increasingly high numbers of solutions demand great
calculation resources. This is why the use of those
methods that give an exact solution to the problem is
not recommended. Instead heuristic and
metaheuristic methods are favoured, methods
capable of solving the problem in an almost exact
way in a reasonable amount of time.
ACO (Ant Colony Optimization) metaheuristic
(Asmar et al, 2005) has proven to be especially
useful when solving problems like TSP, QAP, SP…
ACO is directly inspired in the behaviour shown by
ant colonies when they are foraging (Corne et al,
1999). So we can accurately suppose that ACO is
also effective when applied to the complete road
transport fleet management problem. There are
several different ACO algorithms that can be used
when solving this problem, so our first objective will
be to find the one that better suits each one of the
two parts into which we have divided the fleet
management problem (route calculation and
resource assignment).
The study we performed and now feature in this
document is focused in the comparative analysis of
each one of the ACO algorithms and in their
practical implementation in order to solve the above
mentioned problems. Once they have been analysed
we will be able to pick the most efficient algorithm
for the given task, ready to face the challenge. In
those first steps of the investigation we will restrict
to the use of static parameters, in order to later
535
Antón-Rodríguez M., Boto-Giralda D., J. Díaz Pernas F. and F. Díez Higuera J. (2006).
ACO BASED METHOD COMPARATION APPLIED TO FLEET MANAGEMENT PROBLEM.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 535-539
DOI: 10.5220/0001216105350539
Copyright
c
SciTePress

introduce the dynamic features that better show the
always changing conditions of the road ways.
After briefly introducing this document’s
framework, some of the main characteristics of the
problem will be described (below in §2). Later, in
§3, we will see the efficiency trials taken, their
results and, finally, the conclusions derived from
them (in §4).
2 PROBLEM’S DESCRIPTION
The problem to solve can be described as the need
of, given a number of freights that have to be carried
from some places to others (e.g. from a warehouse to
clients, from one client to another, etc) and a fleet of
transport vehicles, perform the given task with the
minimal possible cost. In other words, it is intended
to find the best possible routes (in this first phase,
just distance will be used to consider), and then
assigning them in an efficient way to the transport
freighters (Perozo, 2002).
The route calculation problem, going over a non-
oriented weighted graph used to represent the
Spanish roadways (with 1.26 arcs per node and a
mean distance of 12 km per arc) consists of
searching the minimum cost routes from their
posting places to the final delivery points, from the
vehicles’ starting point to the freights posting places,
and from the delivery points of each freight to the
pick up places. This makes necessary the solving of
many problems. In particular, given n loads and m
transports, it is required the solving of n · (n + m)
different sub-problems, so finding an exact solution
would be a time and resources consuming task.
Once all possible routes are known, it will be
necessary to select the best combination of them, so
it would allow the optimal delivery of the freights
(minimum cost). This part can also be portrayed
using a graph, where the minimal distances are the
arcs’ weights and the nodes are either loads or
trucks. The described graph will have some nodes
representing trucks (one-way only and not reachable
from other nodes) that can get to any load, and from
those loads they can access to any other. It must be
taken into account that distances (costs) are
asymmetrical. For easing the problem, each truck
will only have capacity for a load at a time, so it will
have to complete a delivery in order to pick up the
next one.
The final solution to the problem must include the
resource allocation data (which freight and in which
order are they picked up by the transport), the
sequence of roadway points travelled, the distance
traversed by each truck and by the fleet as a whole
(being this last one the parameter to optimize).
The problem’s solution will be sought using a newly
developed meta-heuristic known as Ant Colony
Optimization (ACO). This is based on the imitation
of social insect’s behavioural patterns or Swarm
Intelligence (Bonabeau et al, 1999). Ant System (AS)
is an ACO algorithm proposed by Marco Dorigo
(Dorigo et al, 2004) as a useful way of finding a
heuristic solution to combinational problems. AS
can be adapted and optimized to face many
combinational problems, creating new versions of
the algorithm in the process: Elitist Ant System
(EAS) (Dorigo et al, 2004), Rank-Based Ant System
(AS
rank
) (Bullnheimer et al, 1997), MAX-MIN Ant
System (MMAS) (Stützle et al, 1999), Best-Worst
Ant System (BWAS) (Cordón et al, 2000), Ant
Colony System (ACS) (Dorigo et al, 1997). All those
algorithms share the inspirited use they make of the
stigmergy, which is the way ants communicate to
one another.
3 PERFORMANCE TESTS
The developed application is a software program
written in C language and is destined to implement
some ACO algorithms over a basic road network
(not considering, by now, dynamic conditions and
supposing some reasonable restrictions for the sake
of simplicity), with the objective in mind of
obtaining a systematic performance measure system
in the resolution of the cost-optimal route calculation
and resource allocation.
All testing has been conducted using a 1.5GHz
Pentium Mobile equipped computer, with 512Mb
DDR and running on MS Windows XP.
As the given objective was the performance measure
of the different ACO algorithms, some relatively
reduced size graphs have been used (smaller sections
of the general graph which depicts the Spanish road
network). Those graphs come in growing sizes, they
comprise from a small piece of a province up to a
size lager than several regions.
ICINCO 2006 - ROBOTICS AND AUTOMATION
536
The output data will provide the routes (a sequence
of nodes) found for each one of the sub-problems,
alongside the distance calculated for this route.
Because it is statistically interesting, some info
about the algorithm used is also given, execution
time, colony’s size, and values of some relevant
parameters, the total distance (sum of all routes) and
the total number of ants needed to give the proposed
solutions.
3.1 Route Calculation Module
The first step must be to find out the quality of the
found solution. This is the main determining
parameter, as our final objective is to minimize the
cost associated to that solution. By taking into
account the sum of distances of all best solutions
found at each sub-problem, we come by the graphic
shown below:
Figure 1: Sum of all problems’ solutions.
As it can be seen in Figure 1, with a sufficiently high
number of ants per iteration the differences between
algorithms are scarce, but we see that AS
rank
and
EAS are the most effective because of the quality of
their solutions. On the other hand ACS seems to
have a worse global behaviour (the worst solution).
Moreover, there is also some irregular conduct
depending on the colony’s size: almost all the
algorithms (in the global) trace asymptotic curves
towards what is considered to be the ideal solution,
but there are some variations to that trend. This is
the case of ACS, finding a worse solution with 256
agents than the one found with just 128.
In both cases, ACS offers the worst behaviour. This
is due to how the algorithm works, diminishing the
pheromone quantity in an arc previously used by any
agent, choosing, generally, the one which provides
the most info. This is good if there are many
possible arcs, as the sooner some pheromone is
withdrawn from any of them, the quicker some of
the remaining others would become the one with a
maximum value of combined information. However,
in our problems, the number of neighbours is scarce;
so it would take many agents in order to have a
significant reduction in the trail. If this process is
repeated in many nodes, this algorithm can get to be
quite inefficient as it can be seen in our results.
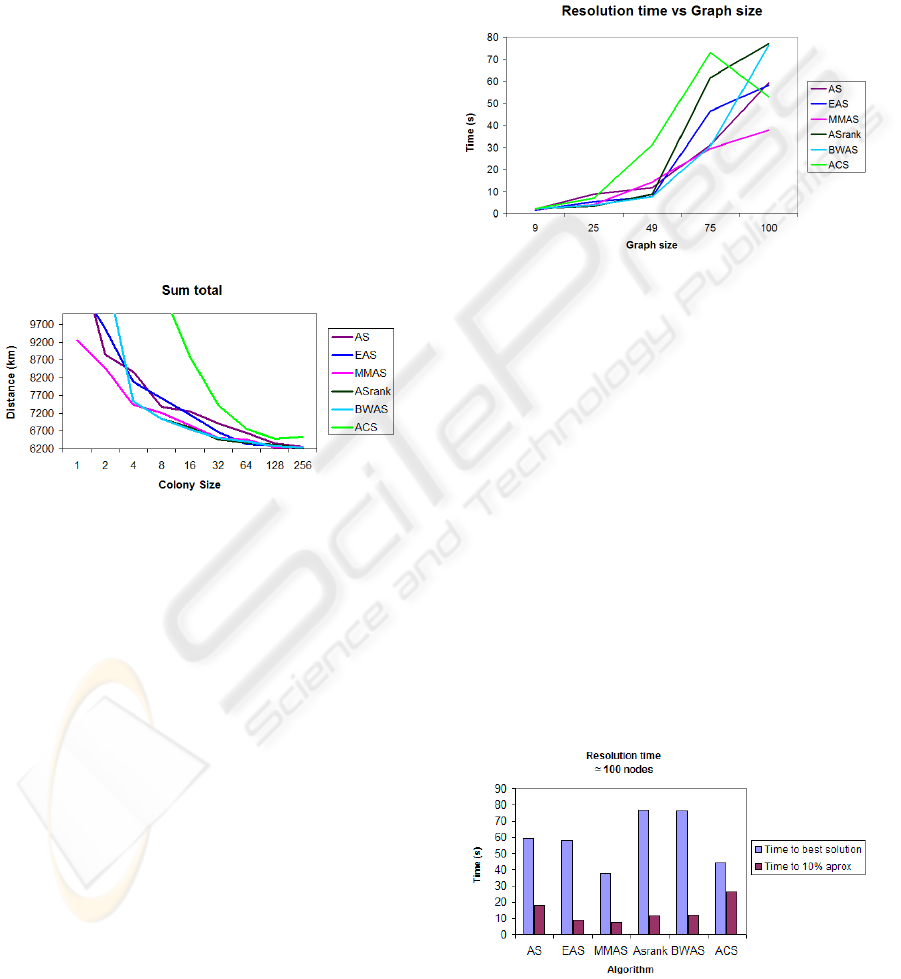
Figure 2: Time taken to find the best solution.
Checking the time taken in each one of the graphs in
order to reach the best solution (Figure 2), it can be
seen that MMAS is the fastest in the last two graphs.
However, AS
rank
, is the algorithm obtaining the
highest quality solutions but takes too much time to
reach a solution due to the need of classifying the
colony’s ants depending on the quality of their
proposed solution; this has a great computational
cost if the colony is composed of many agents.
BWAS also suffers from the same problem.
As the graph which provides us with the most
information is the larger one, two graphics are
shown below with the results. The first one depicts
the resolution times over this graph (the time it takes
the algorithm to find the best solution it is capable
of, and then a solution which differs only in a 10%
from the original one) and in the second, some data
about time and the quality of the solution are shown.
Figure 3: Times for the 100 nodes problem.
ACO BASED METHOD COMPARATION APPLIED TO FLEET MANAGEMENT PROBLEM
537

Figure 4: Time-solution for the 100 nodes problem.
Watching both graphics (Figure 3 and Figure 4)
corroborates the already reached conclusions:
• The algorithm with the best performance
(quality of the solutions found) is AS
rank
even if
the resources and time expense are higher than
in the rest of the algorithms.
• ACS presents a far from ideal behaviour due to
the own nature of the problem: this algorithm
tends to show better performances in problems
with a higher number of arcs per node.
• EAS and MMAS perform well as they have the
shortest execution times, but their solutions, not
being too bad, are not the best found.
3.2 Resource Allocation Module
All data used in this module’s performance study
have been obtained from the 100 nodes graph (4
trucks and 10 loads), as it is the one which provides
us with the most information. The solutions
corresponding to the shortest distance route have
been obtained with AS
rank
(8 ants, rank 6, α=1, β=2,
ρ=0.1) and this very same solution space will be
used as the allocation module entry block.
Figure 5: Distances run in allocations performed with
different colony’s sizes.
For those big enough colonies, all of the algorithms
present reasonably good solutions. However, as can
be seen in Figure 5, the quality of the solutions
frequently shifts with the number of ants used in
each iteration. In some cases the lack of stability is
showy, as is the case of MMAS, AS
rank
and BWAS
algorithms which offer a very changing behaviour.
ACS instead does not only manage to get the best
solution (using a reasonable number of agents), but
it also maintains its stability, this is to say: a bigger
colony means a better solution.
The explanation to this behaviour is the same given
when the algorithm offered the worst performance in
the optimal route calculation module: it is the
relation among the number of nodes and arcs. In the
case of this road network, there is a mean value of
1.26 arcs per node, offering the agents relatively few
options when advancing to the next node.
Nevertheless, in the case of the 100 node graph with
4 trucks and 10 loads there are 130 arcs for a total of
14 nodes. Therefore, the exploration capabilities of
the ACS are ideal for this kind of graph, emphasized
by the random nature of the trucks’ selection: as
some pheromone is withdrawn from each arc as
soon as it is travelled, the possibility of the next
agent searching a new destination is highly powered.
This way, the exploration of a high number of
possibly optimal combinations is quite extensive.
Figure 6: Distance sum of the found solutions.
This good behaviour’s stability can be seen in Figure
6 where the sum of all solutions obtained for all the
different colonies’ sizes, in this ACS offers the best
performance, while all the rest of them offer a
slightly worse behaviour (up to a 1.5% in the case of
BWAS).
Generally, those algorithms that comprehensively
exploit the best solution found do have a more
irregular behaviour than those with wider search
options. This is partly due to the resource (vehicles)
allocation system used. This way, if in the first
iterations some not very good solutions are found,
the trend will be to look for better ones around those,
ICINCO 2006 - ROBOTICS AND AUTOMATION
538

this is why other solutions will not be quite
traversed, creating lock situations around not so
optimal solutions.
Figure 7: Solving time sum for every algorithm.
In Figure 7 it can be seen as all the algorithms show
similar resolution times, with the exception of
AS
rank
, but this is quite logical due to the nature of
the algorithm, as it ranks groups of ants, which of
course takes some calculation power in the ordering
and selection of the agents depending on the quality
of the solution found.
4 CONCLUSIONS
The many daily problems that appear in road
transport show the great need of applications
destined to help in the management of road fleets;
applications capable of finding the best possible
routes, and assigning them efficiently to the different
vehicles that form up the fleet. This is why it is
important to make the right choice of the algorithm
better suited for the problem to solve.
ACO meta-heuristic has some very beneficial
features for the resolution of this kind of situations:
it is capable of finding and optimal or quasi-optimal
solution in a reasonable time, it can optimize
multiple criteria simultaneously and it can be
adapted to work in a dynamic environment. But
these optimization techniques present themselves
under several different algorithms; this is why we
will have to choose what algorithm use in order to
solve each part of the problem.
Once all performance testing and the studies of those
algorithms over the solution of the transport fleet
management problem (both the optimal route
calculation and the resource allocation) were over
we were able to see that there are two algorithms
whose solutions’ quality stood out from the rest:
• The AS
rank
algorithm finds the best solution to
the route calculation problem, but its time and
resources consumption is something higher than
the rest of the algorithms (it can get better using
other ordering faster method). However when it
gets to the resource allocation module, it shows
a more irregular behaviour, spends more time
than the rest and does not easily find the optimal
solution.
• ACS is far from ideal in the route calculation
module; it is however the best in the allocation
part: it finds the higher quality solutions; it is
quite stable and offers a reasonable execution
time.
After analyzing the conclusions shown in this
document, the next step will be the incorporation of
dynamic parameters to the system (road network
status, weather conditions, etc.) when determining
the optimal route.
REFERENCES
Asmar, D. C., Elshamli, A., Areibi, S. A Comparative
Assessment of ACO Algorithms Within a TSP
Environment. DCDIS 2005, Guelph, Ontario, Canada.
July 2005.
Bonabeau, E., Dorigo, M. and Theraulaz, G. Swarm
Intelligence: From Natural to Artificial Systems,
Oxford University Press, 1999.
Bullnheimer, B., Hartl, R. F., Strauβ, C. A new Rank-
Based Version of the Ant System – A Computational
Study. Technical Report, Institute of Management
Science, University of Vienna, 1997.
Cordón, O., Fernández, I., Herrera, F. and Moreno, L. A
New ACO Model Integrating Evolutionary
Computation Concepts: The Best-Worst Ant System.
From Ant Colonies to Artificial Ants: Second
International Workshop on Ant Algorithms
(ANTS'2000), pp. 22-29. Brussels (Belgium), 2000.
Corne, D., Dorigo, M. and Glover, F. New Ideas in
Optimization, McGraw-Hill. 1999.
Dorigo, M. and Di Caro, G. and Gambardella, L. M. Ant
Algorithms for Discrete Optimization. Artificial Life,
5(2), 137-172. 1999.
Dorigo, M. and Gambardella, L.M. Ant colony system: a
cooperative learning approach to the travelling
salesman problem. IEEE Transactions on Evolutionary
Computation,1(1):53-66. 1997.
Dorigo, M. and Stützle, T. Ant Colony Optimization.
Massachussets Institute of Technology. 2004.
Perozo Rondón, F. J. Sistema de gestión dinámica de
flotas usando localización GPS/GSM y programación
evolutiva para la optimización de recursos. Tesis
doctoral. University of Valladolid, 2002.
Stützle, T. and Hoss, H. MAX-MIN Ant System. Preprint
submitted to Elsevier Science, 5. November 1999.
ACO BASED METHOD COMPARATION APPLIED TO FLEET MANAGEMENT PROBLEM
539
