NEURAL NETWORK BASED DATA FILTERING FOR POSITION

TRACKING OF AN UNDERWATER VEHICLE

M. Ufuk Altunkaya, Serhat İkizoğlu

Electrical Engineering Dept., Istanbul Technical University, Istanbul, Turkey

Fikret Gürgen

Computer Eng. Dept., Boğaziçi University Istanbul, Turkey

Keywords: INS, inertial navigation, piecewise neural networks, acceleration data, filtering, backpropagation, radial

basis, position estimation.

Abstract: As a side effect of the developments in the mobile robotics, navigational technology has gained a leap

recently. Although the most popular navigational aid for trajectory tracking is the Global Positioning

System (GPS), it has also some disadvantages. Therefore attentions are drawn to other navigational devices

such as Inertial Navigation Systems. Taking the underwater implementations of vehicle navigation into

account, INS becomes a necessity due to communicational problems between the GPS and the satellites. On

underwater vehicles Inertial Navigation Systems consisting of Inertial Measurement Units (IMU) such as

accelerometers and gyros are used combined with other navigational devices like GPS or sonar. The error of

the IMU output makes it necessary to be accompanied by an additional device. In this paper a neural

network based filtering system is introduced that is planned to be used for the trajectory tracking of an

underwater vehicle.

1 INTRODUCTION

Today several systems are used for accurate position

tracking of vehicles. Among them the most

commonly used one is the Global Positioning

System (GPS). But even this system is not perfect,

and some additional units are employed to correct

the data given by the GPS. Generally an Inertial

Measurement Unit (IMU) is utilized for this

purpose. The whole system is called an Inertial

Navigation System (INS). Recently there is a trend

to omit the GPS due to its unreliability at certain

situations. As GPS uses satellites, it cannot be used

whenever the connection with the satellites is

corrupted (due to poor satellite geometry, high

electromagnetic interference, high multipath

environments, or obstructed satellite signals). In

addition, the INS system provides much higher

update positioning rates compared with the output

rate conventionally available from GPS (Hiliuta et

al, 2004). Also this system is strategically dangerous

as it is used for military purposes.

2 THE SYSTEM

Our aim in this study is the accurate tracking of an

underwater vehicle which can travel without any

external guidance. Therefore, an IMU (Microstrain

3DM-G) that consists of a 3D-accelerometer, a 3D-

gyroscope and a 3D-magnetometer is chosen for this

purpose. Using this device, the position tracking can

be done by double integrating the acceleration data.

But if there is any noise or bias at the output data of

the accelerometer, then this error will increase with

each integration step. To overcome this problem the

output data must be filtered. There are different

methods used for filtering the sensor data, from

conventional filters to Kalman filtering. This paper

introduces the study of a signal filtering method

depending on neural network methodology. For this

purpose Matlab and Simulink programs are used.

Both the reading process of the acceleration data and

teaching the neural network are done by Matlab

while Simulink is used for the simulation of the

197

Ufuk Altunkaya M., Ä

rkizo

glu S. and Gürgen F. (2006).

NEURAL NETWORK BASED DATA FILTERING FOR POSITION TRACKING OF AN UNDERWATER VEHICLE.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 197-200

DOI: 10.5220/0001216901970200

 SciTePress

position tracking for the previously prepared neural

network models.

2.1 Errors of the Inertial Sensors

In the IMU, there are two main sources of error that

occur at the inertial sensors: The sensor bias and the

noise of the sensor data. (Other errors are scale

factor and axes misalignment, (Hou, 2004)).The

bias for accelerometers and gyros is described as the

output value for zero input. The effect of the bias of

an accelerometer on the velocity and position

calculations is:

∫∫

∫

===

21 tbtdtbvdtpe

tbdtbve

(1)

where

pebve

stand for velocity error, sensor bias

and position error respectively. Also the effect of the

noise upon the position calculation is similar. Since

ve and pe would increase with time, it is very

important to filter the disturbing signals.

2.2 Filtering Methods

Advanced filtering methods like the Kalman Filter

are mostly preferred for high precision filtering. By

these methods, also called the Stochastic Modeling

Methods, first the error is modeled, and then this

calculated error is filtered. Haiying Hou (2004) has

made a comparison of the Kalman Filter and some

other stochastic modeling methodologies.

Great care must be taken for determining the

coefficients of the Kalman Filter and modeling.

Since in our system the sampling rate is determined

due to the performance of the computer Matlab is

running on, it’s hard to model the system from the

samples taken. On the other hand, as our aim is to

design a system that can be employed in different

environments and on different types of vehicles, we

prefer a model-free concept. Thus, using a neural

network based learning algorithm that can be trained

in the form of the real data would result in a better

filtering.

3 THE STUDY: NEURAL

NETWORK BASED FILTERING

Although neural network based systems are recently

used for trajectory tracking they are mostly

employed in INS-GPS integrated applications

(

Noureldin et al, 2004, Kaygisiz et al, 2003). In these

applications neural networks are trained to follow up

the position of the vehicle and are aimed to converge

to the INS position data in order to trace the route in

the absence of the GPS.

3.1 Algorithm Comparison

In our study we first compared network architectures

using the two main algorithms: The Multi-layer

Perceptron Backpropagation Feed-forward Networks

and the Radial Basis Neural Networks.

In order to compare the algorithms we need a

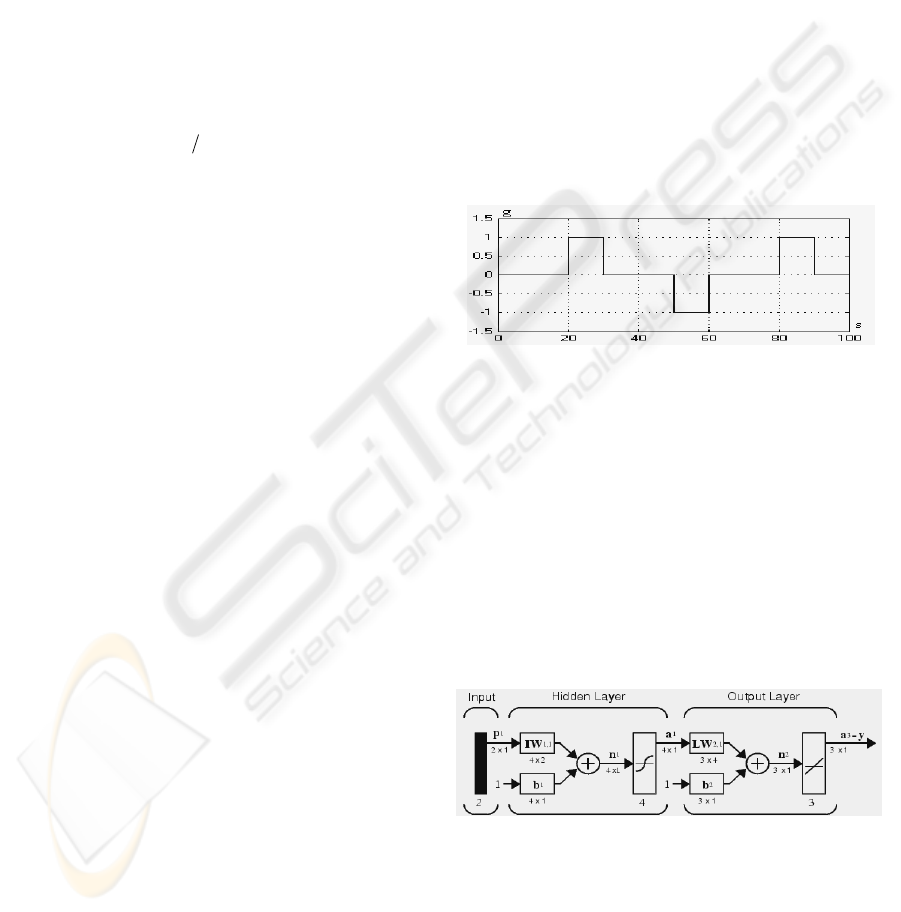
“known” signal and a noisy one. The signal with 1g

amplitude in Figure 1 forms our “known” signal.

The noisy signal is constructed as the superposition

of the known signal and the output data of the sensor

for the steady state that constitutes the noise-data.

Figure 1: The “known” acceleration data.

3.1.1 The Backpropagation Algorithm

The Back-propagation method, sometimes also

called the generalized delta rule, is commonly

applied to feedforward multilayer networks. Here

the weights and the biases are adjusted by error-

derivative (delta) vectors back-propagated through

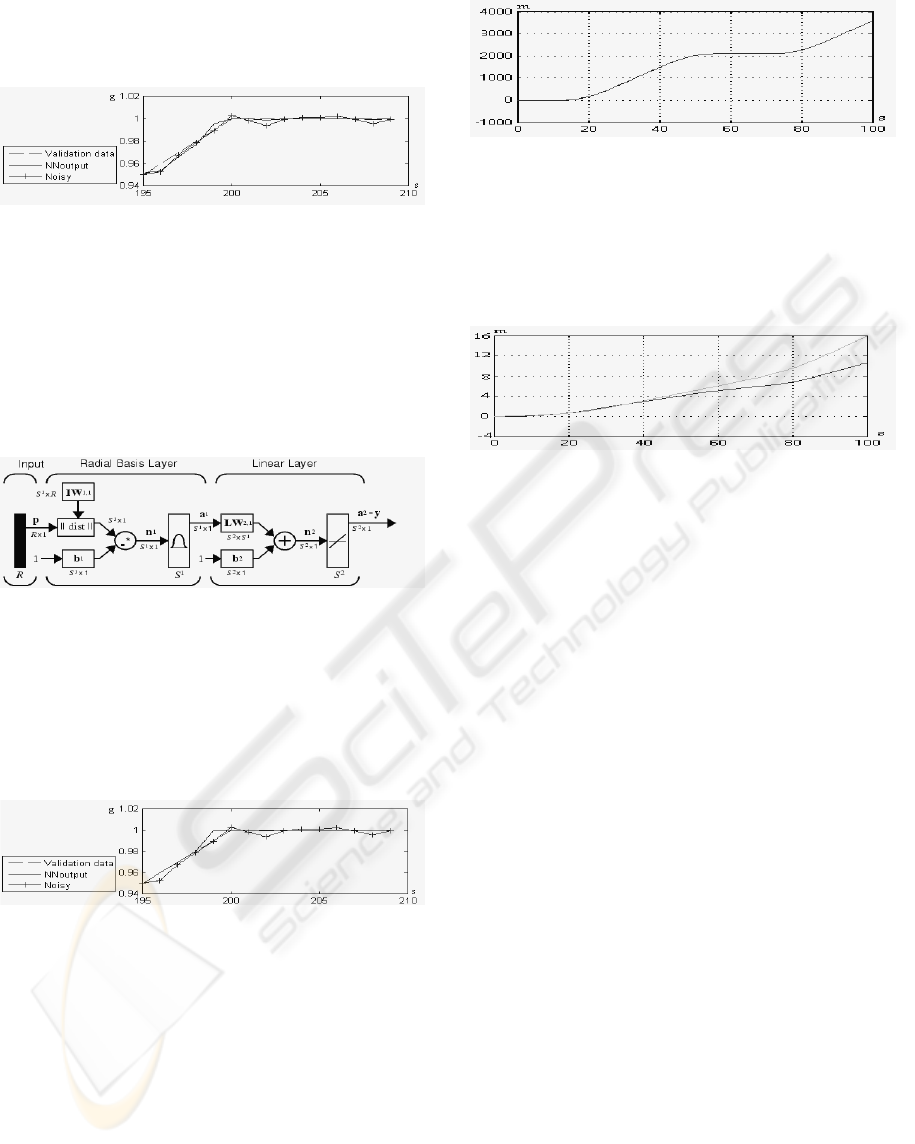
the network. Figure 2 shows the architecture of a

feedforward neural network using the

backpropagation algorithm with one hidden layer of

sigmoid neurons and an output layer of linear

neurons.

Figure 2: Back-propagation Neural Network Architecture.

In this study following network architectures

using back-propagation algorithms are trained and

compared: Gradient Descent (GD), Gradient

Descent with Momentum Back- Propagation

(GDM), Gradient Descent with Adaptive Learning

Rate Back Propagation (GDX) and Levenberg-

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

198

Marquardt Back Propagation (LM). Among these

Levenberg-Marquardt methodology has given the

best result (Figure 3).

Figure 3: Training with Levenberg-Marquardt Algorithm.

3.1.2 The Radial Basis Neural Network

The Radial Basis Function is a curve fitting method

applied in multi-dimensional space. A radial basis

neuron acts as a detector that produces 1 whenever

the input p is identical to its weight vector w. The

bias b allows the sensitivity of the neuron in the

radial basis layer to be adjusted (Figure 4).

Figure 4: Radial Basis Neural Network Algorithm.

For comparison, Radial Basis Network (RB),

Exact Radial Basis Network (RBE) and

Generalized

Regression Neural Network (GRNN) architectures

are trained. Due to the comparison the Generalized

Regression Neural Network has given the best

convergence as shown at Figure 5.

Figure 5: Training with Generalized Regression

Algorithm.

3.1.3 Back-Propagation vs. Radial Basis

Neural Network

The two best trained architectures using different

algorithms are compared within the Matlab/Simulink

model of the system.

The position data obtained by double integrating

the “known” acceleration data is given in Figure 6:

Figure 6: The true position data.

Comparing the two networks denotes that

filtering with the backpropagation neural network

(lighter line) ends up with an error of about 5m more

than the one using the radial basis network (darker

line) over a 4000m distance (Figure 7).

Figure 7: Errors of the radial basis and the back-

propagation network outputs for position data.

Although they may require more neurons

comparatively, the Radial Basis Networks can be

trained in a much shorter time than the standard

feedforward networks. Therefore we have chosen

Radial Basis Neural Network architecture as the

optimum network for our study.

3.2 Methods to Obtain Accurate

Position Tracking Using Neural

Network Based Optimisation

After choosing the optimum neural network

algorithm, we designed different filtering

architectures to get the best position estimation using

the acceleration data of the vehicle.

Whilst filtering the noise on the acceleration

output, the true data also deforms causing an error

which increases with each integration. Therefore, we

decided to compare the results for filtering the

velocity and position data respectively.

3.2.1 Velocity-Data Filtering

After filtering the noisy velocity data, position

estimation is obtained by integrating the velocity

data once. The errors of the filtered and the noisy

data are given in Figure 8, the darker line

representing the filter output.

NEURAL NETWORK BASED DATA FILTERING FOR POSITION TRACKING OF AN UNDERWATER VEHICLE

199

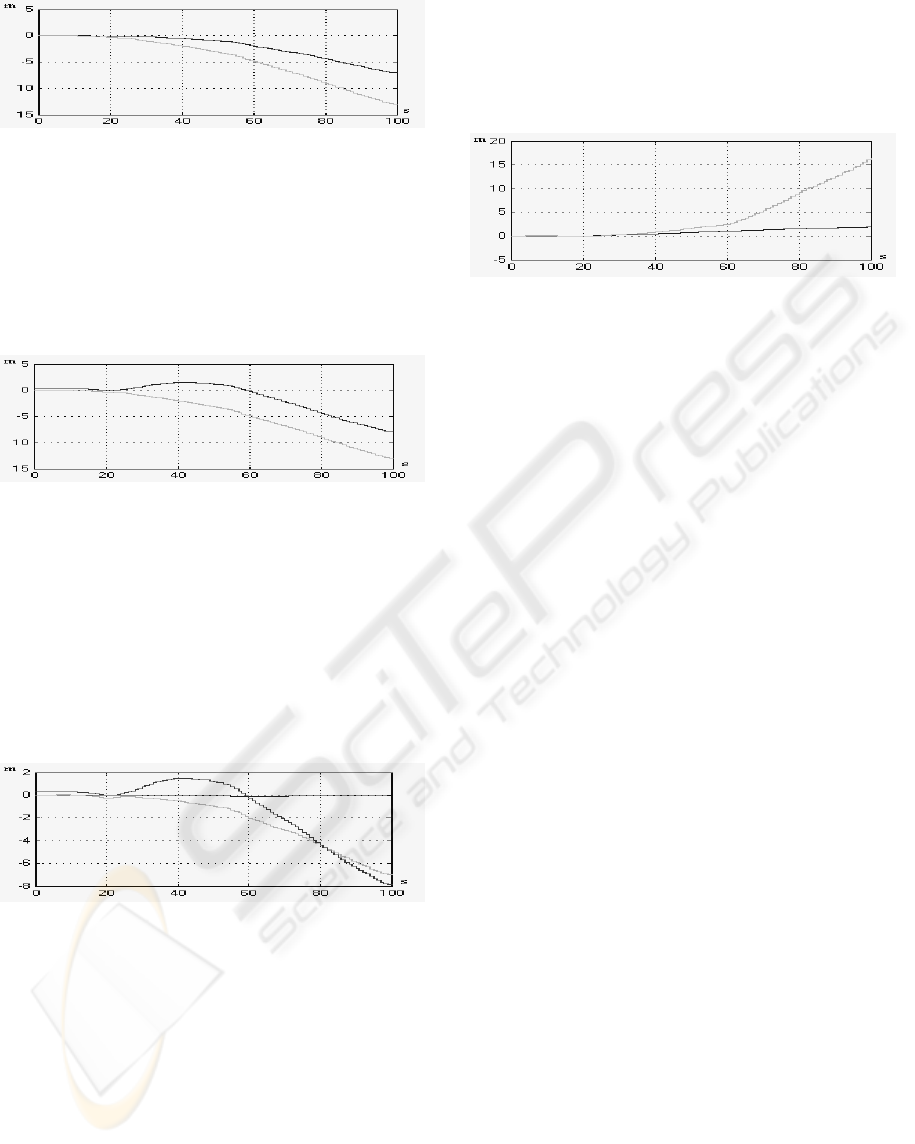
Figure 8: Position errors of the integrated noisy and filtered

velocity data.

3.2.2 Position-Data Filtering

The errors given in Figure 9 belong to the noisy

position data obtained by double integrating the

noisy acceleration data, and the filtered noisy data.

(The dark line represents the filtered signal.)

Figure 9: Errors of the noisy and filtered position data.

The comparison of the three filtering processes

applied for different versions of the data leads to the

conclusion that filtering the acceleration data gives

the best result (Fig. 10). The closest (light) line to

the horizontal axis at zero value represents the

output of acceleration filtering. The data with

positive hunch values correspond to the output of

position filtering and the third curve describes the

output of velocity filtering.

Figure 10: Comparison of position data obtained from

acceleration, velocity and position filtering.

3.2.3 Filtering with Piecewise Trained

Networks

Constructing a system composed of neural networks

each of which is trained for a special situation can

provide dynamic position estimation.

A switching model, containing neural networks

trained for different phases of input as zero input,

increasing / decreasing input and non-zero constant

value input is designed. The system uses the specific

neural network to filter for the specific part of the

data whenever the system detects the input in any of

these forms. Thus the system can adapt to different

trajectories of the vehicle.

The system tested with the “known”

acceleration data (Figure 1) is observed to filter the

noise with a high accuracy as seen in Figure 11.

Figure 11: Position errors of the Piecewise Neural

Network (darker line) and the noisy data.

4 CONCLUSION

In this study neural network based filtering models

are tested using data sets constructed from the

readouts of an IMU and user-defined signals in order

to simulate the trajectory of an underwater vehicle

with good estimations of position data. As the

piecewise neural network filter offers the best

performance among all and also gives satisfactory

results, we have decided to use this method for our

further practical studies.

REFERENCES

Hiliuta, A., Landry, R. JR., Gagnon, F., 2004. Fuzzy

Corrections in a GPS-INS Hybrid Navigation System.

In IEEE Transactions on Aerospace and Elecronic

Systems Vol. 40, No.2.

Hou, Haiying (2004) Modeling Inertial Sensors Errors

Using Allan Variance, Department of Geomatics

Engineering, The University of Calgary, Calgary,

Canada.

Kaygisiz, B.H.; Erkmen, A.M.; Erkmen, I. 2003 GPS/INS

Enhancement Using Neural Networks For

Autonomous Ground Vehicle Applications. Intelligent

Robots and Systems, (IROS 2003)

Noureldin, Aboelmagd; Osman, Ahmed, El-Sheimy,

Naser 2004 A Neuro-Wavelet Method For Multi-

sensor System Integration For Vehicular Navigation.

Journal of Measurement Science and Technology,

Volume 15, Issue 2, pages 404-412.

ICINCO 2006 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

200