
FINDING A COMMON QUADRATIC LYAPUNOV FUNCTION
USING CONICAL HULLS
Rianto Adhy Sasongko
Control and Power Group, Department of Electrical and Electronic Engineering, South Kensington Campus,
Imperial College London, London SW7 2AZ, United Kingdom
J. C. Allwright
Control and Power Group, Department of Electrical and Electronic Engineering & Centre for Process Systems Engineering,
South Kensington Campus, Imperial College London, London SW7 2AZ, United Kingdom
Keywords:
Positive semidefinite matrices, cone, conicall hull.
Abstract:
Consider a set of linear time-invariant continuous-time systems that is a convex hull with vertices formed by a
given set of systems. The problem of finding a common Lyapunov function v, specified in terms of a symmetric
positive definite matrix, for the convex hull of systems is tackled by searching for a symmetric positive definite
(PD) matrix P which causes dv/dt to be negative definite for each vertex system. The approach involves an
extension of an existing method for solving optimization problems for positive semidefinite (PSD) matrices
that is based on a representation of the cone of PSD matrices as a conical hull. The condition that the derivative
of the Lyapunov function for each vertex system is negative definite is converted naturally into the condition
that the matrix P belongs to the interior of the intersection of several conical hulls: one for each vertex system
to ensure dv/dt for it is negative definite. The determination of a P in the intersection is viewed as the
solution of a quadratic programme on the product space of the cones. Then the existing theory and algorithms
for conical hull problems are adapted to the solution of the quadratic programme. The numerical results
suggest that the proposed algorithm is faster than the projective method used in MATLAB for small problems.
Effort is being devoted to improve it for larger problem.
1 INTRODUCTION
For a family of dynamical linear continuous-time sys-
tems, obtaining a common Lyapunov function (CLF)
is desirable to ensure stability of all systems in the
convex hull of that set of systems or stability when the
system transits from one vertex of the convex hull to
another at any time (D.Liberzon, 2003). The impor-
tance of a common Lyapunov function for stabiliza-
tion of switched linear systems is discussed in (G.Xie,
2004), and the existence of a common Lyapunov
function for a set of asymptotically stable systems is
examined in (N.A.Bobylev, 2002) and (R.N.Shorten,
2003). An algorithm for obtaining a common Lya-
punov function, called the gradient method, is dis-
cussed in (D.Liberzon, 2003). A semidefinite pro-
gramming algorithm, called the projective method,
(A.Nemirovskii, 1994) can also be used for solving
such problems.
Here a new algorithm is proposed for finding a
common Lyapunov function; it is based on the con-
ical hull approach to the description of the set of sym-
metric positive semidefinite matrices, which will be
introduced later.
Let S denote the set of symmetric matrices from
R
n×n
. Let S
≥
be the set of positive semidefinite ma-
trices, and S
>
the subset of positive definite matrices,
from S.
For a set of N stable A
i
∈ R
n×n
, i = 1 : N ,
the function v(x) = x
T
P x is a common Lyapunov
function for the A
i
if P ∈ S satisfies
A
T
i
P + P A
i
< 0, ∀i ∈ [1 : N]
(1)
Solving (1) for such a P is a semidefinite program-
ming problem with the symmetric positive definite
matrix P as the variable.
In the following analysis, it will be convenient to
describe such P by vec(P), which is the vector con-
sisting of the entries of P in a certain order. In de-
tail, vec(P ) = [P (1, :)
T
; P (2, :)
T
; . . . ; P (n, :)
T
] ∈
R
n
2
(using MATLAB notation). Of course, P =
vec
−1
(p). Consequently condition (1) can be written
as:
M
i
p ∈ vec(S
>
) , ∀i ∈ [1 : N]
p ∈ vec(S
>
)
(2)
for
M
i
= −(A
T
i
⊗ I + I ⊗ A
T
i
) ∈ R
n
2
×n
2
(3)
113
Adhy Sasongko R. and C. Allwright J. (2006).
FINDING A COMMON QUADRATIC LYAPUNOV FUNCTION USING CONICAL HULLS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 113-118
DOI: 10.5220/0001218001130118
Copyright
c
SciTePress

where ⊗ denotes the Kronecker product.
Since the A
i
are asymptotically stable, the M
i
are
non-singular. Therefore P = vec
−1
(p) solves (1) if
and only if
p ∈ M
−1
i
vec(S
>
), ∀i ∈ 1 : N
p ∈ vec(S
>
) ,
(4)
or if and only if p ∈ int(I), the interior of I, where I
is defined by
I =
(
N
\
i=1
M
−1
i
vec(S
>
)
)
(5)
The solution p needs to be in the interior of I to guar-
antee the positive definiteness of the corresponding
matrix P = vec
−1
(p).
Hence, there is a CLF of the form v(x) = x
T
P x if
and only if
I 6= ∅ (6)
and the problem of solving (1) is equivalent to that of
finding an interior point p of the intersection I, assum-
ing it has one.
The main contribution here is the development of
a computational method for finding a vector p in
interior(I), if there is one.
We have chosen to investigate the above formula-
tion since the other obvious formulation
min
P
i
∈S
≥
i=[0:N]
N
X
i=1
kP
i
+A
T
i
P
0
+P
T
0
A
i
k
2
+kP
0
−βIk
2
(7)
leads to one additional conical hull being involved
(the purpose of β, a positive scalar, will become clear
near (22)).
The material is presented in the following way.
Some descriptions and properties of a conical hull
representation of the set of symmetric PSD matrices
is given in Section 2. An approach for finding a point
in the interior of I using the conical hull approach is
outlined in Section 3. More detail about the solution
of the CLF problem using conical hulls is also given
in this section. Numerical procedure and some results
for the CLF problem are given in Section 4. Finally,
the conclusions are given in Section 5.
2 A CONICAL HULL FOR PSD
MATRICES
2.1 Conical Hull Characterization
for Symmetric PSD Matrices
The background theory of symmetric matrices can
be found in various references, some of them are
(R.A.Horn, 1985) and (G.Strang, 1988). The de-
finitions of this section and the basic conical hull
theory and approach used throughout this paper
are from (J.C.Allwright, 1988) and (J.C.Allwright,
1989); most of the proofs can be found in these pa-
pers.
Symmetric PSD matrices are defined uniquely by
their diagonal and upper triangle of elements, so
vec(S) = {vec(A) : A ∈ S} is a subset of a linear
subspace of R
n
2
that has dimension r = n(n + 1)/2.
An orthonormal basis for that subspace can easily be
found. For instance, for the case n = 3, suitable ba-
sis vectors are w
1
= e
1
, w
2
= (e
2
+ e
4
)/
√
2, w
3
=
(e
3
+e
7
)/
√
2, w
4
= e
5
, w
5
= (e
6
+e
8
)/
√
2, w
6
= e
9
where e
i
= [0 0 . . . 0 1 0 . . . 0]
0
with the 1 in row i.
The corresponding basis matrix is
W = [w
1
w
2
. . . w
r
] ∈ R
n
2
×r
(8)
and it is easy to check that W
T
W = I
r
, R[W
T
] =
R
r
and R[W] = vec(S).
Using this basis, vec(A) ∈ R
n
2
can be written in
terms of the vector vec(A) ∈ R
r
as
vec(A) = W vec(A) ∈ R
n
2
(9)
where
vec(A) = W
T
vec(A) ∈ R
r
. (10)
Since, generically, vec(A) contains no redundant
information regarding symmetric A, it can be thought
of as a minimal description of such an A.
Now any matrix A ∈ S
≥
can be written as A = M
2
for some M ∈ S. For example, if the spectral form of
A is written as V ΛV
T
with Λ = diag[λ
1
λ
2
. . . λ
n
]
then such an M is V diag(
√
λ
1
. . .
√
λ
n
)V
T
. Let-
ting B = M(kMk
F
)
−1
, where kMk
F
:=
(
P
n
i,j=1
m
2
ij
)
0.5
is the Frobenius norm, we see that
our general A can be written as A = αB
2
for α ∈
[0, ∞) and B ∈ U := {B ∈ S : kBk
F
= 1}. This
suggests, correctly, that S
≥
= cone{B
2
: B ∈ U}
where cone(X) := {αx : α ∈ [0, ∞), x ∈ X} is the
conical hull of X.
In fact, it will be more convenient to use
vec(S
≥
) = cone(Ω) (11)
where
Ω = conv {Ψ} (12)
for
Ψ =
vec(B
2
) : B ∈ U
⊂ R
n
2
U =
B ∈ R
n×n
: B
T
= B , kBk
F
= 1
(13)
and it is obvious that the set vec(S
≥
) that contains
only the minimal description of every symmetric pos-
itive semidefinite matrix can be written as:
vec(S
≥
) = cone(W
T
Ω) (14)
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
114
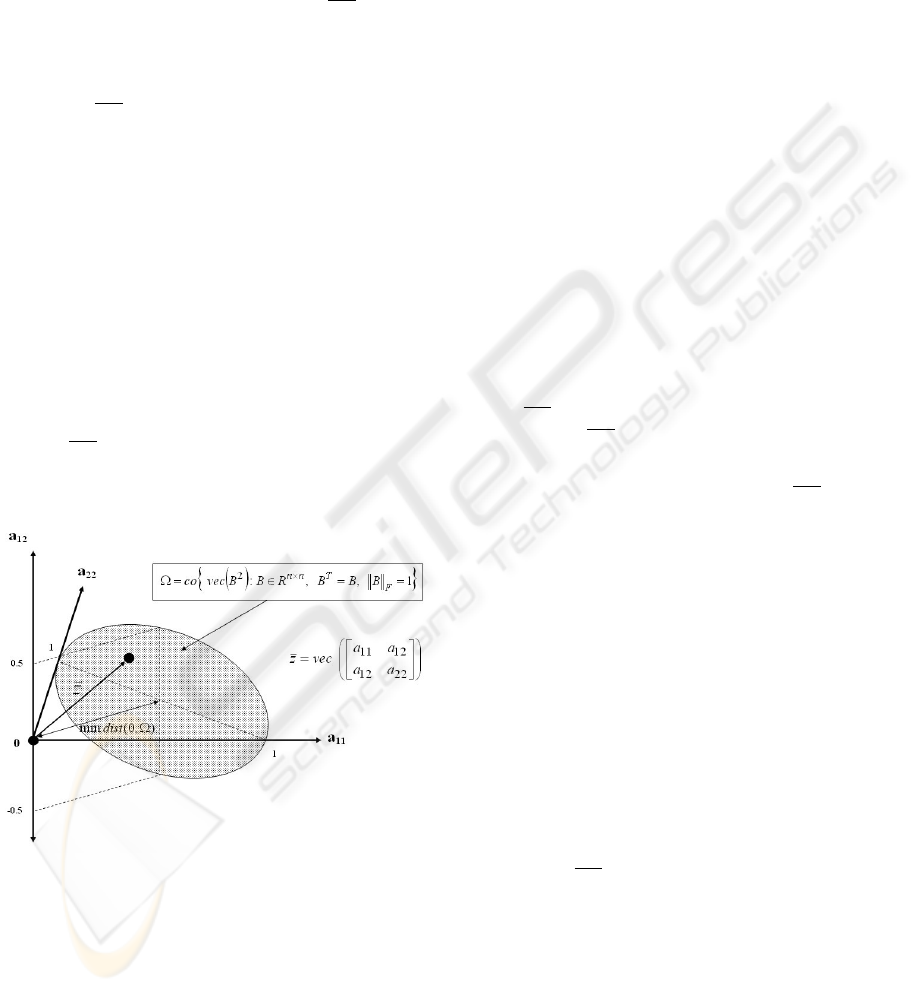
2.2 Properties of our Conical Hull of
Symmetric PSD Matrices
Some definitions and properties of the conical hull
of PSD matrices are presented in this section; this
will be needed for the development of the algorithm.
Recall that vec(S
≥
) = cone(Ω) and vec(S
≥
) =
cone(W
T
Ω) for Ω of (12). Since the set S
>
of
symmetric positive definite matrices is the interior of
the set S
≥
vec(S
>
) = int(cone(W
T
Ω)) (15)
It follows from the definition (12) that Ω is a non-
empty, convex, and compact set, and (not so obvi-
ously) that:
min kxk
2
= n
−1/2
x ∈ Ω
(16)
A consequence of this fact is that:
min kxk
2
= σ
min
(L)n
−1/2
x ∈ LW
T
Ω
(17)
for all L ∈ R
r×r
, where σ
min
(L) is the minimum
singular value of L.
It is interesting that Ω is a subset of an affine subset
of R
r
, which is actually the intersection of an affine
set and (vec(S
≥
), which is a cone. Hence, somewhat
surprisingly, Ω is a ’flat’ set. This is illustrated in the
following figure:
Figure 1: Depiction of Ω.
For the determination of feasible descent directions
later, it will be important to be able to solve easily, for
any vector ¯g ∈ R
r
, the optimization problem:
min ¯g
T
γ
γ ∈ LW
T
Ω
(18)
It turns out that a minimizer ˆγ can be found easily as
ˆγ = LW
T
vec(νν
T
) (19)
where ν is a normalized eigenvector corresponding to
the minimum eigenvalue of Z, with Z defined as:
Z = [vec
−1
(¯g) + vec
−1
]/2 ∈ R
n×n
(20)
for
¯g = W L
T
g (21)
3 OPTIMIZATION ON CONICAL
HULLS
Conceptually the CLF problem is that of finding a
¯z ∈ int(
T
K
i
) where the K
i
are the convex sets
cone(W
T
¯
M
i
Ω). The approach will be to first find
a point in the intersection
T
K
i
and then, if it is not
in the interior, to perturb it into the interior (if there is
one).
The basic idea for finding a point in
T
K
i
is to
find a ¯z
i
in each K
i
such that the distance between
all ¯z
i
is minimized. Then, if the minimal distance is
zero, we have found a point
ˆ
¯z which is in the inter-
section
T
K
i
. Obviously the origin is not in the inte-
rior of the intersection, so to encourage the optimiza-
tion algorithm to find a non-zero point, a penalty term
k¯z
1
− vec(βI)k
2
, with positive real β, is added to the
cost to attract vec
−1
(¯z) towards the positive definite
matrix βI. Hence the problem is
min
¯z
i
∈K
i
i=[1:N]
P
i,j∈[1:N]
i6=j
k¯z
i
− ¯z
j
k
2
+ k¯z
1
− vec(βI)k
2
(22)
which is a convex problem. Next a cone is constructed
as:
K = {K
1
× K
2
× . . . × K
N
} (23)
Then the optimization problem (22) can be reformu-
lated as :
min v(¯z)
¯z ∈ K
(24)
where,
v(¯z) = ¯z
T
¯
Q¯z +
¯
F ¯z
¯
Q =
P
N
i,j=1, i6=j
¯
P
T
E
ij
¯
P
E
ij
+
¯
P
T
1
¯
P
1
¯
F = −2
¯
β
T
¯
P
1
¯
P
E
ij
=
¯
P
i
−
¯
P
j
(25)
Here
¯
β = vec(βI), ¯z = (¯z
1
, . . . , ¯z
N
)
T
with each
¯z
i
∈ K
i
, and the matrix
¯
P
i
selects ¯z
i
from ¯z, in that
¯z
i
=
¯
P
i
¯z.
The set K itself is a convex cone, so the algorithm
of (J.C.Allwright, 1988) for finding the closest point
in cone(Γ) to a point d , i.e. for solving
min kd − xk
2
,
x ∈ cone(Γ)
(26)
can be adapted to solve the optimization problem
above because kd −xk
2
= kdk
2
−2d
T
x + kxk
2
and
FINDING A COMMON QUADRATIC LYAPUNOV FUNCTION USING CONICAL HULLS
115

this has the same form as the cost of (22).
To proceed further, the notion of a truncated cone
is needed . The bounded subset cone
T
(Γ) =
{αx : x ∈ Γ, α ∈ [0, 1]} will be called the trun-
cation of the complete conical hull cone(Γ) =
{αx : x ∈ Γ, α ∈ [0, ∞]}. Then the corresponding
truncated cone K
η
is defined by
K
η
= cone
T
(η
1
W
T
¯
M
1
Ω) × cone
T
(η
2
W
T
¯
M
2
Ω)×
. . . × cone
T
(η
N
W
T
¯
M
N
Ω)
(27)
It turns out that it is easy to compute a positive real
η such that the unknown optimal solution of (22) lies
in the bounded set K
η
. This yields the optimization
problem
min v(¯z)
¯z ∈ K
η
(28)
An algorithm for solving this problem is discussed
next.
3.1 Finding Supporting Hyperplanes
The concepts and algorithm of (J.C.Allwright, 1988)
can now be applied to solve the optimization prob-
lem of (28). At each iteration, it first calculating the
gradient ¯g
k
= 2¯z
T
k
¯
Q − 2
¯
β
T
(
¯
P
T
1
¯
P
1
) of the quadratic
cost v(¯z) . A linearisation about ¯z
k
of v(¯z) is then
provided by v(¯z
k
) + ¯g
T
k
(¯z − ¯z
k
). The next step is to
minimize this linearisation with respect to ¯z from K
η
by solving the problem:
Figure 2: Linear minimization over cone.
min ¯g
T
k
(¯z − ¯z
k
)
¯z ∈ K
η
(29)
For suppose an optimal solution for this problem is
called ˜z
k
. Then ˜z
k
− ¯z
k
is a feasible descent direc-
tion from ¯z
k
and therefore can be used to decrease the
value of the cost fuction v(¯z). It can be seen that the
minimizer will be either in the set ηW
T
¯
M
i
Ω or at the
origin i.e. at the vertex of the cone. An interpretation
of this optimization is that it is finding the supporting
hyperplane for the set K
η
that has normal ¯g
k
. Owing
to the structure of optimization problem (29), this lin-
ear programming problem can be decomposed into N
separate minimization problems
min ¯g
T
i
k
¯z
¯z ∈ K
η
i
i ∈ [1 : N]
(30)
where the gradients ¯g
i
k
are from the partitioning of
the gradient vector ¯g
k
as
h
¯g
1
k
¯g
2
k
. . . ¯g
N
k
i
T
.
According to (18-21), minimizing ¯g
T
¯
(z) over the set
K
η
i
= cone
T
(η
i
W
T
¯
M
i
Ω) will give the following
minimizer:
˜z
i
k
= η
i
W
T
vec(ν
i
k
ν
T
i
k
) (31)
where η
i
is truncation factor for appropriate set and
ν
i
k
is a normalized eigenvector corresponding to the
minimum eigenvalue of Z
i
k
, λ
min
[Z
i
k
], which is de-
fined as:
Z
i
k
=
(vec
−1
(
¯
g
i
k
)) + (vec
−1
(
¯
g
i
k
)
T
)
2
∈ R
n×n
(32)
with,
¯
g
i
k
= W [¯g
T
i
k
W
T
¯
M
i
W ]
T
(33)
Hence the contact point between set K
η
and support-
ing hyperplane H
k
=
¯z
¯g
T
k
¯z = C
is the vector
˜z
k
=
˜z
T
1
k
˜z
T
2
k
. . . ˜z
T
N
k
T
.
3.2 Quadratic Minimization Over a
Polytope
One way to determine a point ¯z
k+1
giving
v(¯z
k+1
) < v(¯z
k
) would be to minimize v(¯z) on
the set {¯z
k
+ ω(˜z
k
− ¯z
k
) : ω ∈ [0, 1]}. This involves
optimization with respect to the scalar ω and is
therefore relatively easy to carry out. This set is a
subset of K
η
so optimization on it can be regarded as
optimization of v(¯z) on an approximation to K
η
. Ob-
viously using a larger approximating set would tend
to give a greater reduction in v(¯z). Such a set can be
obtained as the convex hull of {0, ˜z
k
, ¯z
k−1
, ¯z
k
, . . .}.
Then ¯z
k+1
is chosen as the point in this convex hull
that minimizes v(¯z). A way to do this optimization
on the polytope is outlined next.
Having the contact points available, an approxi-
mation to the set K
η
is given by the convex hull of
the contact points (29) and the optimal points of (28)
from previous iterations. Then the minimizer of (28),
ˆ
¯z, can be calculated by solving a quadratic problem
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
116

over this convex hull, as follows:
Theorem 3.1 : Let
ˆ
¯z
k−N
v
,
ˆ
¯z
k−N
v
+1
, . . . ,
ˆ
¯z
k−1
be the
set of minimizers of the quadratic function v(¯z) over
the convex hull defined at iterations (k − N
v
), (k −
N
v
+ 1), . . . , (k − 1), and let ˜z
k−1
be the minimizer
of ¯g
T
k−1
(¯z − ¯z
k−1
) over K
η
at iteration (k −1). Then
v(
ˆ
¯z
k
) ≤ v(˜z
k−1
) ≤ v(
ˆ
¯z
k−1
) (34)
where,
ˆ
¯z
k
= arg min v(¯z)
¯z∈co
{
ˆ
¯z
k−N
v
,
ˆ
¯z
k−N
v
+1
,...,
ˆ
¯z
k−1
,˜z
k−1
}
(35)
Here co
¯v
1
, ¯v
2
, . . . , ¯v
N
v
represents the convex hull
of the vectors ¯v
1
, ¯v
2
, . . . , ¯v
N
v
and N
v
denotes the
number of vectors used for the convex hull. The inte-
ger k denotes the iteration number.
To solve optimization problem (35), we first repre-
sent the variables ¯z
i
of each set K
i
as a convex com-
bination of ¯v
i
1
, ¯v
i
2
, . . . , ¯v
i
N
v
, i.e.
¯z
i
=
P
N
v
j=1
µ
i
j
¯v
i
j
for
P
N
v
j=1
µ
i
j
= 1, µ
i
j
≥ 0
(36)
for all i ∈ [1 : N] with each v
i
j
∈ R
(r×1)
.
Using this in (35) transforms the problem into the
quadratic programme in ˜µ
min
˜µ∈R
(N
v
×N)×1
˜µ
T
V
T
¯
QV˜µ +
¯
F V˜µ
subject to G
c
˜µ =
¯
1
((N
v
×N)×1)
˜µ ≥ 0
(37)
where
V =
¯
V
1
¯
0
(r×N
v
)
. . .
¯
0
(r×N
v
)
¯
0
(r×N
v
)
¯
V
2
. . .
¯
0
(r×N
v
)
.
.
.
.
.
.
¯
0
(r×N
v
)
¯
0
(r×N
v
)
. . .
¯
V
N
(38)
G
c
=
¯
1
(1×N
v
)
1
¯
0
(1×N
v
)
. . .
¯
0
(1×N
v
)
¯
0
(1×N
v
)
¯
1
(1×N
v
)
2
. . .
¯
0
(1×N
v
)
.
.
.
.
.
.
¯
0
(1×N
v
)
. . .
¯
1
(1×N
v
)
N
(39)
with
¯
V
i
=
h
¯v
i
1
¯v
i
2
. . . ¯v
i
N
v
i
˜µ = [¯µ
1
T
¯µ
2
T
. . . ¯µ
N
T
]
T
¯µ
i
= [µ
i
1
µ
i
2
. . . µ
i
N
v
]
T
; i = 1, . . . , N.
(40)
Here
¯
0
(p×q)
is a p ×q zero matrix and
¯
1
p×q
is a p ×q
matrix with all its entries equal to 1.
The optimal solution,
ˆ
¯z, of the original problem
(35) can then be calculated from the solution
ˆ
˜µ of the
transformed problem (37) using
ˆ
¯z = [V
f
]
ˆ
˜µ (41)
where V
f
is as defined in (38) with its entries formed
from the vectors specifying the convex hull defined in
the last iteration.
The convergence of the sequence ¯z
k
to an optimizer
for optimization problem (22) can be proved in much
the same way that convergence for a similar optimiza-
tion problem was proved in (J.C.Allwright, 1988).
3.3 Correction Using Gradient
It may happen that the solution
ˆ
P = vec
−1
(W
ˆ
¯z
i
)
from (41) above lies on one or more of the boundaries
of the cones K
η
i
, in which case the solution will not
satisfy at least one of the positive-definiteness con-
straints. Even if the all the positive-definiteness con-
straints are satisfied, it might be desired to have a ma-
trix that is not so close to the boundary in that the
smallest eigenvalue of −(A
T
i
P +P A
i
) is undesirably
small. In this case, a correction using the gradients of
the constraints can be incorporated into the algorithm.
This enables a small update δP to be applied to the so-
lution
ˆ
P to give the modified solution
ˆ
P + δP where
the correction can be obtained by finding a δ
˜
P that
makes the following inequalities hold for all j:
P
l,m∈[1:n]
∂λ
j
(
˜
M(i))
∂P
l,m
δ
˜
P
l,m
≤ 0, i ∈ I
−
P
l,m∈[1:n]
∂λ
j
(
˜
M(i))
∂P
l,m
δ
˜
P
l,m
< 0, i ∈ I
0
P
l,m∈[1:n]
∂λ
j
(
˜
M(i))
∂P
l,m
δ
˜
P
l,m
< 0, i ∈ I
+
(42)
Here (l, m) is the index of the elements of
ˆ
P =
vec
−1
(
ˆ
¯z), and
˜
M(i) = A
T
i
P + P A
i
. I
−
, I
0
, and
I
+
denote the index of sets where the initial point
ˆ
P
lies inside the corresponding set, on its boundary or
outside, respectively. It is obvious that for i ∈ I
−
,
i ∈ I
0
, and i ∈ I
+
, the value of
˜
M(i) will be nega-
tive, zero, and positive respectively.
The gradient can obtained from:
∂λ
j
(
˜
M(i))
∂P
l,m
= x
j
x
T
j
(43)
with x
j
is the eigenvector corresponding to the eigen-
value λ
j
(
˜
M(i)). The δ
˜
P will make the inequalities
in (42) hold, and it can be used for updating δP i.e.
we can set δP = ωδ
˜
P by choosing an appropriate
scalar ω > 0, so that all constraints are satisfied by
the corrected solution.
4 NUMERICAL CALCULATION
4.1 The Algorithm
The algorithm then is implemented in numerical cal-
culation for solving our convex problem. The algo-
rithm is arranged as follows:
FINDING A COMMON QUADRATIC LYAPUNOV FUNCTION USING CONICAL HULLS
117

1. set k = 0, choose initial point ¯z
0
, error bound >
0, number of vertices of the convex hull N
v
, and
calculate basis matrix W and
¯
M
i
for all i
2. set ¯z = ¯z
k
3. calculate cost value v(¯z
k
) and the gradient ¯g
k
, then
find the the contact point
˜
¯z
k
between set K
η
and
hyperplane H
k
by solving ¯g
T
k
¯z (29)
4. for co {¯z
k
, ¯z
k−1
, . . . , ¯z
k−N
v
+1
,
˜
¯z
k
}, if k < (N
v
−
1) then set ¯z
k−1
, . . . , ¯z
k−N
v
+1
= 0, form V and
G
c
, and calculate V
T
¯
QV and
¯
F V
5. solve the quadratic programming problem (37) to
get the minimizer
ˆ
¯z
k
, and calculate v(
ˆ
¯z
k
) and the
lower bound b
low
= v(¯z
k
) + ¯g
T
k
(
ˆ
¯z
k
− ¯z
k
)
6. if v(
ˆ
¯z
k
)−b
low
< then stop, otherwise set ¯z
k+1
=
ˆ
¯z
k
and k = k + 1 and go to step 2
7. perform correction procedure of section 3.3 if nec-
essary
4.2 Numerical Results
The algorithm has been tested for finding a com-
mon Lyapunov function for a various problems. The
results were compared with those of the projective
methods (A.Nemirovskii, 1994) available in the MAT-
LAB LMI toolbox. A common symmetric PD matrix
P was found after finite iterations using the conical
hulls, and the computing times for it are listed in 2nd
row of table 1. The 3rd row shows the processing time
for the correction procedure. The conical hull algo-
rithm and the MATLAB algorithm were executed 100
times to observe the consistency of the time calcula-
tions. Since the latest version of MATLAB exploits
the JIT-accelerator, converting the M-script to C/C++
code (MEX-file) would not have improved the execu-
tion time.
Table 1: Numerical Results - Processing time (seconds).
n = 10 N = 2 N = 4 N = 6 N = 10
C − Hull 0.003 0.0502 0.11 0.384
(corrct) 0.023 0.0411 0.0576 0.06
P rojM et 0.0633 0.0805 0.1063 0.2484
The results show that the conical hull algorithm
is faster for N = 2, 4. As the number of inequal-
ities increases, the conical hull algorithm becomes
slower, compared to the projective method. Since the
proposed method uses distance minimization between
points in all the cones, as the number of inequalities
rises, the number of variables will also rise signifi-
cantly. Probably, the reason the conical hull algo-
rithm performs less well for bigger problem is that
the QP involved at each iteration becomes relatively
more costly to execute. To overcome this problem,
an efficient way for managing the variables should be
explored. It should be noticed that the proposed algo-
rithm guarantees all the inequalities are satisfied ac-
curately.
5 CONCLUSIONS
A new algorithm has been presented, based on the ex-
isting conical hull theory, for solving the problem of
finding a common quadratic Lyapunov function for
a family of stable dynamical systems. The numeri-
cal results suggest that the algorithm is better than the
projective method for small problems. Further devel-
opments will be carried out to improve it for larger
problems and apply it to control studies.
ACKNOWLEDGEMENTS
The first author would like to thank the Islamic De-
velopment Bank (IDB) who provides the fund that en-
ables him to undergo the project.
REFERENCES
A.Nemirovskii (1994). The projective method for solving
linear matrix inequalities. Proceedings of the Ameri-
can Control Conference, pages 840–844.
D.Liberzon (2003). Gradient algorithm for finding common
lyapunov functions. 42nd IEEE Conference on Deci-
sion and Control, pages 4782–4787.
G.Strang (1988). Linear algebra and its applications. Har-
court Brace Jovanovich, San Diego, 3 edition.
G.Xie (2004). Stability and stabilization of switched linear
systems with state delay: continuous-time case. 16th
Mathematical Theory of Networks and Systems Con-
ference.
J.C.Allwright (1988). Positive semidefinite matrices : Char-
acterization via conical hulls and least-squares solu-
tion of a matrix equation. SIAM journal of Control
and Optimization, 26:537–556.
J.C.Allwright (1989). On maximizing the minimum eigen-
value of a linear combination of symmetric matrices.
SIAM journal on Matrix Analysis and Applications,
10:347–382.
N.A.Bobylev, e. (2002). On the stability of families of dy-
namical systems. Differential Equations, 38(4):464–
470.
R.A.Horn (1985). Matrix Analysis. Cambridge University
Press.
R.N.Shorten (2003). On common quadratic lyapunov func-
tions for pairs of stable lti systems whose system ma-
trices are in companion form. IEEE Transactions on
Automatic Control, 48(4):618–621.
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
118
