DATA FLOW FORMALIZATION

Thouraya Bouabana-Tebibel

Institut National d’Informatique BP 68M, Oued-Smar 16270, Algiers, Algeria

Keywords: UML, OCL, Petri nets, temporal logics, verification, validation.

Abstract: The Object Constraint Language OCL is an extension of the UML notation for the expression of restrictions

on diagrams. We propose to take advantage of its all expression capabilities for validating the UML system

properties. For this purpose, we develop an approach to support the OCL invariant verification on the

colored Petri nets derived from the UML modeling. A case study is given throughout the paper to illustrate

the approach.

1 INTRODUCTION

UML (OMG, 2003) suffers from ceaseless critics on

the precision of its semantics when the verification

of modeling correctness has become a key issue.

UML 2.0 (OMG, 2004) brings more precision on its

semantics, but it remains informal and lacks tools for

automatic analysis and validation. We presented in

(Bouabana-Tebibel, 2004) a methodology to

automatically derive UML modeling in colored Petri

nets (Jensen, 1992) which are supported by lots of

tools to verifying them. In the present paper, we

carry on with this work by developing a technique to

deal with the verification process.

The Petri nets resulting from the derivation

processes, are analyzed by means of PROD (PROD,

2004), a model checker tool for predicate/transition

nets. Model checking is classified as the most

appropriate technique for verifying operational UML

models (Beato, 2004), (Ober, 2003). It allows a fast

and simple way to check whether the property holds

or not. To avoid the high cost learning of the model

checker, the designer can specify the system

properties in OCL, the Object Constraint Language

(OMG, 2003) which permits to formulate

restrictions over UML models, in particular,

invariants. The latter can be after, automatically

translated to temporal logic properties in order to be

verified by PROD during the Petri net analysis.

Translating OCL invariants into LTL and CTL

properties remains insufficient for validating the

properties. Indeed, OCL expressions refer to

classifiers to evaluate their association ends. The

association ends values are updated (created,

modified or read) on the object life cycle by means

of the link actions. So, in addition to the OCL

invariant translation in LTL and CTL properties, we

propose an approach to translate the link actions in

Petri nets, to achieve the systematic formal

verification of the OCL constraints.

The remainder of the paper starts with a brief expose

on the UML modeling derivation to Petri nets, this,

constituting the background of the present work. The

proposed approach is then presented and the

techniques upon which it is based are developed.

These techniques are illustrated in a case study. We

conclude with some observations on the obtained

results and recommendations on future research

direction.

2 BACKGROUND

We summarize in this section, the work that we

present in (Bouabana-Tebibel, 2004) to derive UML

statecharts to colored Petri nets. This work supports

the approach that we develop in the present paper.

2.1 Statecharts

A statechart describes the behavior of a class in

terms of states and exchanged messages with other

classes’ statecharts. A state is composed of two

atomic actions (at its entry and its exit) and one

activity. The states are linked by means of

transitions annotated with the event that triggers the

transition (event trigger) and atomic actions

148

Bouabana-Tebibel T. (2006).

DATA FLOW FORMALIZATION.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 148-153

DOI: 10.5220/0001219501480153

 SciTePress

produced by the triggered transition. Due to their

atomicity, the entry, exit and transit actions are in

fact, generated events respectively called: entry, exit

or transit events, see figure 1.

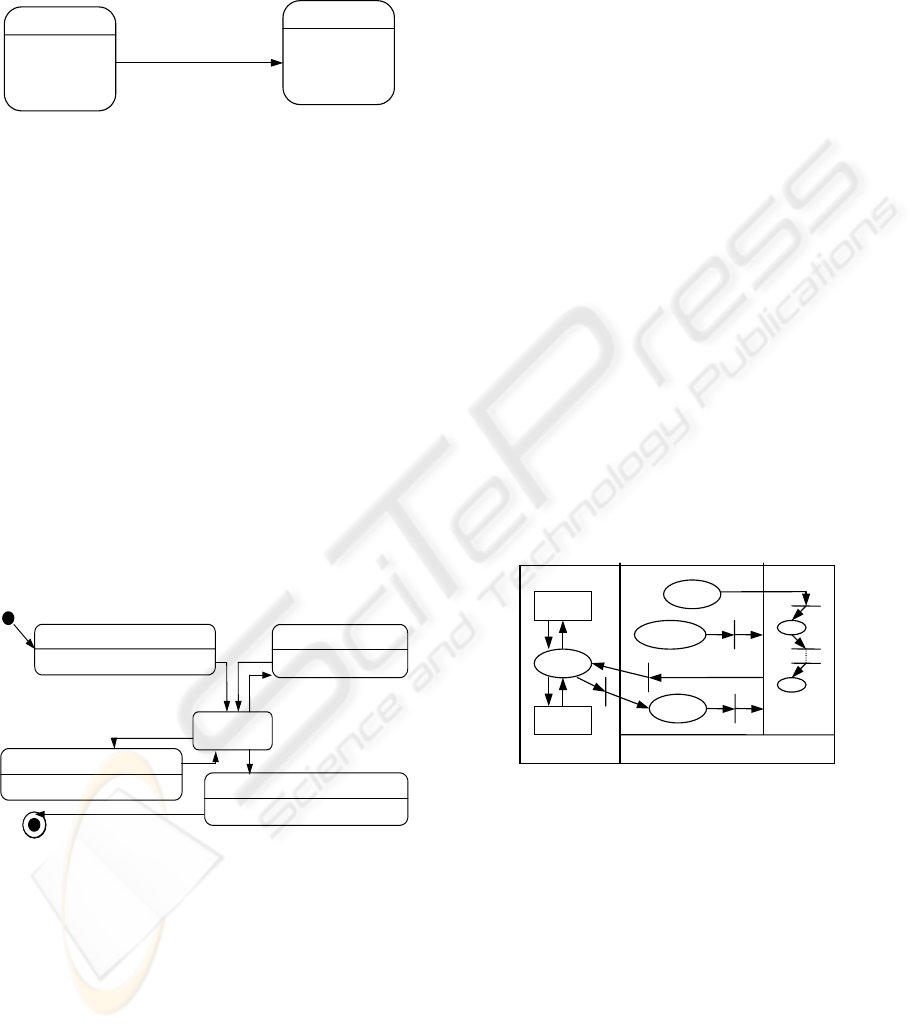
State 2

entry: event

do: activity

exit: event

trigger / transit event

State 1

entry: event

do: activity

exit: event

Figure 1. Statechart’s events and activity

The event is of two types: send event or call event.

These events are mentioned on the statechart as

follows: «send» class(), «call» operation().

Examples of these events are given in the case study

of figure 2.

We illustrate our study through a message server

application where the main role of the server is to

manage the communication between the connected

stations. All the exchanged messages must go

through this server, to be forwarded to the receivers.

Figure 2 represents the statechart of a station which

can, at all times, connect itself from the server. Its

connection request is realized using the «send»

connection event. The server confirms the station

connection using the «send» okconnection events.

When connected, a station can notify a message,

receive a message or disconnect itself. It notifies by

means of the «send» notification event.

entry : «send» connection()

connecte

entry : «send» disconnection()

disconnection

connection

«send» okconnection()

/ «create» notification()

sen

okdisconnection

()

rece

tion

exit : «call» save()

«send» forward()

entry : «send» notification()

notification

Figure 2. Statechart of the station class

After receiving a forwarded message from the server

by means of the «send» forward trigger, it saves it

using the «call» save event. Its disconnection is

requested by the «send» disconnection event and

confirmed by the «send» okdisconnection event.

2.2 Petri Nets

Petri nets have been presented in several works

(Baresi, 2002) as a suitable formalism for translating

the UML dynamic models. We used them in

(Bouabana-Tebibel, 2004) to derive the statechart

and collaboration diagrams. We defined them by the

7-tuple <P, T, A, C, Pre, Post, M

,> where:

- P = {p

, p

, …, p

} is a set of places.

- T = {t

, t

, …, t

} is a set of transitions.

- A ⊆ P × T ∪ T × P, is a set of arcs.

- C = {C

, C

, …, C

} is a set of colors where C

{<c

, c

…, c

>} and c

is a variable or a constant.

- Pre : P

T → P(C) is a precondition function to

the transition firing such that Pre(p

, t

) = {C

, C

, …,

- Post : P

T → P(C) is a postcondition function to

the transition firing such that Post(p

, t

) = {C

, C

…, C

: P → C is the initial marking function, such that

) = ∑

k=1,K

2.3 Derivation Approach

The derivation process is based onto an object-

oriented approach. Each statechart modeling an

interactive class behaviour is transformed to an

object subnet called Dynamic Model or DM (see

figure 3). To construct the DM, each state s

∈

S is

converted to a place p

∈

P and each transition tr

∈

Tr is converted to a transition t

∈

The classes interact through the Link place which

receives the events generated by the DMs and then

dispatches them to the destination DMs. The

forwarding is relayed by the Input place which

constitutes an input interface of the DM. The events

are modeled by tokens of event type

To deal with Petri net simulation, we tackle the Petri

net initial marking which may be of two types: static

or dynamic. The static initial marking provides the

class instances and their attribute values. These

instances are extracted from the object diagram to

initialize the Object place with tokens of object type

of the form <obj, attrib>. The dynamic initial

OPN

Link

OPN

Input

Object

Scenario

Figure 3. Petri nets interconnection architecture

Figure 1: Statechart’s events and activity.

Figure 2: Statechart of the station class.

Figure 3: Petri nets interconnection architecture.

DATA FLOW FORMALIZATION

149

marking provides the exchanged messages among

the interactive objects. These messages are extracted

from the sequence diagram to initialize the Scenario

place with tokens of event type. The event tokens

have the form <srce, targ, op/xobj, attrib> where

Srce and targ are respectively the source object’s

identity and the target object’s identity. The

component op/xobj gives the called operation if a

call event and the exchanged object’s identity if a

send event. As for attrib, it designates the set

{attrib

, …, attrib

}of the exchanged object’s

attributes if a send event, the operation attributes if a

call event.

Thus, each generated event on the statechart is

converted to an arc from the Scenario place to the

transition to which it is related. It is after converted

to an arc from this transition to the Link place. As

for the event trigger, it is converted to an arc from

the Input place to the transition on which it occurs.

Figure 4 represents the Petri net resulting from the

conversion of the statechart of the station class.

3 ANALYSIS AND

VERIFICATION

The verification by model checking as treated in

PROD, is based on the state space generation and

the verification of safety and liveness system’s

properties on this space. The properties may be

basic, about the correctness of the model

construction or specific, written by the modeler to

ensure the faithfulness of the system modeling. For

each of these approaches, given a property, a

positive or negative reply is obtained. If the property

is not satisfied, it generates a trace showing a case

where it is not verified.

3.1 Generic Property Verification

The basic properties are verified according to on-

the-fly tester approach or the reachability graph

inspection approach. The on-the-fly verification of a

property means that the property is verified during

the state space generation which is automatically

stopped as soon as the property fails, in contrary to

the traditional approach where properties are

verified on the reachability graph, after its

generation.

The on-the-fly tester approach detects deadlock,

livelock and reject states. The deadlock verification

ensures that there exists no reachable marking where

no transition is enabled. In other words, that means

that there is no UML states that prevent any activity

to be invoked eventually. The livelock detection

informs about loops of actions on the graph. As for

the reject state checking, it detects undesirable

markings in critical places which is equivalent in

UML, to rejecting undesirable objects at given

states. These three properties are systematically

verified, without intervention of the designer.

The reachability inspection approach permits the

verification of some other properties such as quasi-

liveness, boundedness or reinitializability. These

properties are automatically verified.

The quasi-liveness property is weaker than the

deadlock. It guaranties that each transition is enabled

at least once, i.e., each UML activity can be invoked

eventually.

The boundedness is formulated to require an upper

bound to the number of objects that can be present,

in a state at a given time or in an association end,

according to the UML specification using the

multiplicity construct. Since objects correspond to

tokens, this property upper-bounds the number of

tokens.

The reinitializability property checks the possibility

for a system of restarting from any state, i.e., the

initial marking should be reachable from any

marking of the net. This is realized by a systematic

computation of the net strongly connected

components which must be equal to 1, so that the net

can be reinitializable.

3.2 Specific Property Verification

For a more precise validation, system’s specific

properties can be written by the designer in LTL or

CTL logics and then, verified by PROD. Since the

connectio

Input

notification

disconnection

reception

connected

Lin

Scenario Object

Figure 4. OPN of the station class

Figure 4: OPN of the station class.

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

150

main motivation of this work is that the UML

designer may reach a valid modeling without needs

for knowledge of formal techniques, it is only

reasonable that the properties are expressed by the

modeler in the OCL language and are after,

automatically translated in LTL and CTL logics.

Many works have investigated the OCL invariant

translation in other formalisms such as Object-Z

(Roe, 2003), B (Marcano, 2002), first-order

predicate logic (Beckert, 2002) or object-based

temporal logic (Distefano, 2000). Other works

tackled OCL invariant extension with temporal

operations (Cengarle, 2002), (Flake, 2004). The

relevance of such a mapping is of a practical nature.

It presents the merit of providing a specific

translation that takes the target tool’s (PROD)

characteristics into account. Due to the paper length,

this translation is presented in another work.

OCL is mainly based on collection handling in order

to specify object invariants. As these collections

correspond to association ends, the latter must

appear on Petri net specification so that the

translated LTL and CTL properties (whose

expression is essentially made of these constructs),

can be verified. This lead us to the necessity of

introducing the association end modeling onto the

statecharts in order to get after transformation, the

equivalent Petri net constructs. This object flow

modeling is realized by means of the link actions.

However, the usefulness of the link actions does not

concern explicitly the modeling of the object life

cycle. When constructing his diagrams, the designer

does not necessarily think to modeling these

concepts which are rather specific to the link and

end object updates. For example, for connecting a

station to the server, the connection request and

connection confirmation actions are naturally and

systematically modeled by the designer, but the

addition of the connected station to the association

end is usually omitted from the modelling, see

figures 2 & 5. That is why we recommend to the

designer to specify the link actions on the statechart

so that the OCL invariants can be verified. But, we

release him from this modeling on the sequence

diagram and take in charge the treatments related to

the initialization of these actions.

UML action semantics was defined in (OMG, 2001)

for model execution and transformation. It is a

practical framework for formal descriptions. For this

work, we are particularly interested in the create link

and destroy link. The create link action permits to

add a new end object in the association end. The

destroy link action removes an end object from the

association end. These actions will be represented on

the statechart as tagged values of the form

{linkAction(associationEnd)}, following the event

which provokes the association end update.

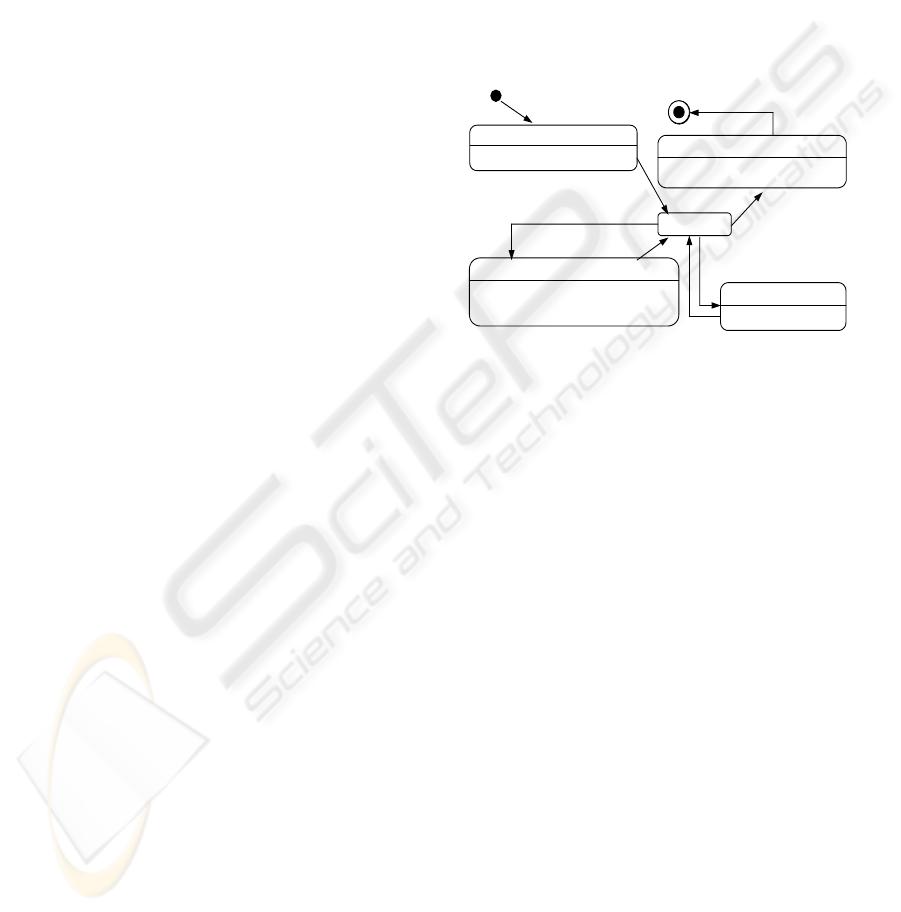
On figure 5, after confirmation of its connection or

disconnection («send» okconnection or «send»

okdisconnection), the station adds or removes itself

from the association end connectedStation, using

respectively, {createLink(connectedStation)} or

{destroyLink(connectedStation)}. It adds a notifed or

received message with {createLink

(transmittedMessage)} or

{createLink(receivedMessage)}, respectively.

The link actions may concern an active (interactive)

or passive (exchanged) end object. The object-

oriented approach, on which both UML and Object

Petri nets rely, is based on modularity and

encapsulation principles. To deal with modularity, a

given association end should appear and be

manipulated in only one statechart. In Petri nets, the

association end is translated in a place of role type.

This place holds the name of the association end and

belongs to the DM translating the statechart.

Furthermore, an association end regrouping active

objects must be updated within the statechart of

these objects’ class, in order to comply with the

encapsulation concept. Indeed, since the end object

is saved in the role place with its attributes, these

attributes must be accessible when updating the

association end. The exchanged objects are usually

manipulated by the interactive objects and are not

specified by dynamic models. So, the association

end representing them could be updated in the

statechart of the class that is at the opposite end. As

more than one opposite end can be linked, the

selected class is the one affecting the association

end. For exchanged objects, the encapsulation

constraint is lifted given that the exchanged object’s

entry : «send» connection()

connecte

entry : «send» disconnection()

disconnection

connection

«send» okconnection()

{createLink(connectedStation)}

/ «create» notification()

«send» okdisconnection()

{destroyLink(connectedStation)}

receptio

exit : «call» save()

«send» forward()

{createLink(receivedMessage)}

entry : «send» notification()

{createLink(transmittedMessage)}

notification

Figure 5. Statechart of the station class with link action specification

Figure 5: Statechart of the station class with link action

specification.

DATA FLOW FORMALIZATION

151

attributes are transmitted within the message and so,

accessible by the interactive objects.

In Petri nets, the create link action is semantically

equivalent to an arc from the transition related to the

association end update towards the place specifying

the association end, adding an object within. The

destroy link action is semantically equivalent to an

arc from the association end place to the transition

corresponding to the link action, removing an object,

see figure 6.

The object to be added to / removed from the

association end is extracted from the components of

the token (whose global form is <srce, targ, op/xobj,

attrib>) corresponding to the event that provokes the

association end update. This token is situated in the

Scenario place if the event is generated. It is located

in the Link place if the event occurs. The

added/removed object may be the source object (src)

or the exchanged object (xobj) if the link action

follows a generated event. It is the target object

(targ) or the exchanged object (xobj) if the link

action follows an event trigger.

In Petri nets, the association end objects are colored

tokens of role type They are of the form <assoc, obj,

attrib>, where obj is the object to be added to or

removed from the association end and assoc is the

object at the opposite end.

We propose in what follows, to express a property

extracted from the server message application. This

property is first expressed into a paraphrased

(textual) form. It is after, specified as OCL

invariants and finally translated into LTL properties.

Property 1

The number of connected stations is limited to

maxStation.

Property 1 expression in OCL

context s:Server inv: s.connectedStation→size <=

Server.maxStation

Property 1 expression in PROD

For each server s and for each place of its DM

write

the property:

# verify henceforth (card(connectedStation : field[0]

== s) <= (place

DM*server

: field[2]))

where:

- connectedStation: field[0] designates the first

component (assoc) of the connectedStation’s tokens,

- place

DM*server

: field[2] designates the third

component (attrib

= maxStation) of the tokens of

DM* of the server,

- DM* designates a DM excluding the places of role

type.

4 CONCLUSION AND FURTHER

WORK

Formalization of UML statechart semantics (Kuske,

2001), (Truong, 2005), (Varro, 2002) and integration

in the statecharts of formal languages state-oriented

(Attiogbé 2003), (Meyer, 2001) or property-oriented

(Attiogbé 2003), (Royer, 2003) were widely

investigated in the research area. The OCL language

has also been used in various works in particular,

those of Flake (Flake, 03), (Flake, 04) who extends

it with temporal logics to express properties over

time. However, through our multiple investigations,

we have never encountered works that tackle the

integration of the end associations on the statecharts

to formalize the object flow dynamics.

This paper presents an approach to systematically

validate the UML modeling without need for the

user to know formal checking techniques. The

verification concerns both the correctness of the

model construction and the faithfulness of the

modeling. The latter is allowed thanks to the system

awaited properties which are expressed by the

modeler in OCL language and then translated into

LTL and CTL properties. To efficiently deal with

their validation, we propose to introduce an object

flow specification into the object’s control flow

model (statechart), using predefined actions on the

association ends.

An extension of this work concerns the automatic

translation of the OCL invariants to LTL and CTL

properties according to PROD syntax and features.

This work is actually under review. Another

prospect of this paper is the analysis of the

validation/verification results and their feedback to

the user are explored. These results must be

presented to the designer in an interpreted form,

where the error in modeling is simply and clearly

pointed out. Since the methodology calls for UML

Statechart constructs Petri net constructs

{

CreateLink(role)}

role

derivation

role

{

DestroyLink(role)}

Figura 6. Translation of the link actions

Figure 6: Translation of the link actions.

ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

152

designer to provide the input specifications, it is only

reasonable for the output results to be meaningful to

that user.

REFERENCES

Attiogbé, C., Poizat, P., Salaun, G., 2003. Integration of

Formal Datatypes within State Diagrams, In M. Pezze

éds. Fundamental Approaches to Software

Engineering FASE’2003, LNCS, vol. 2621, pp. 341-

355, Springer.

Baresi, L., 2002. Some Premilinary Hints on Formalizing

UML with Object Petri Nets, Proc. of the 6th World

Conference on Integrated Design & Process

Technology, Pasadena, USA.

Beato, M. E., Barrio-Solorzano, M., Cuesta, C. E., 2004.

UML Automatic Verification Tool (TABU), In proc.

ACM SIGSOFT Symposium on the Foundations

of Software Engineering, October/November.

Beckert, B., Keller, U., Schmitt, P., 2002. Translating the

Object Constraints Language into First-order Predicate

Logic, Proc. Verify, Workshop at Federated Logic

Conferences, Copenhagen.

Bouabana-Tebibel, T., Belmesk, M., 2004. From UML

towards Petri nets to specify and verify, Proc. ICINCO

2004, 1

International Conference on Informatics in

Control, Automation & Robotics, Portugal.

Cengarle, JM., Knapp, A., 2002. Towards OCL/RT, In L.-

H. Eriksson and P. Lindsay, eds., Formal Methods –

Getting IT Right, LNCS, vol 2391, Springer, July, pp.

389-408.

Distefano, D., Katoen, J-P., Rensink, A., 2000. On a

Temporal Logic for Object-Based Systems, Proc.

Fourth International Conference on Formal Methods

for Open Object-Based Distributed System”,

FMOODs 2000, Stanford, California, USA,

September.

Flake, S., Mueller, W., 2004. Past- and Future-Oriented

Temporal Time-Bounded Properties with OCL, Proc.

2nd Int. Conf. on Software Engineering and Formal

pp. 154-163.

Flake, S., 2003. UML-Based Specification of State-

oriented Real-time Properties, PhD thesis, Faculty of

Computer Science, Electrical Engineering and

Mathematics, Paderborn University, Shaker Verlag,

Aachen, Germany.

Jensen, K., 1992. Coloured Petri nets, Vol 1: Basic

Concepts, Springer.

Kuske, S., 2001. A formal semantics of UML state

machines based on structured graph transformation,

M. Gogolla and C. Kobryn, ed. UML: The Unified

Modeling Language. Modeling Languages, Concepts

and Tools, LNCS vol. 2185, pp. 241-256.

Marcano, R., Lévy, N. 2002. Transformation rules of OCL

Constraints into B Formal Expressions, In University

of Versailles Saint-Quentin-en-Yvelines eds.

Meyer, E., 2001. Développements formels par objets :

utilisation conjointe de B et d’UML, PhD thesis,

LORIA, University of Nancy 2, France.

Ober, I., Graf, S., Ober, I., 2003. Validating Timed UML

Models by Simulation and Verification, Proc.

International Workshop SVERTS: Specification and

Validation of UML Models for Real Time and

Embedded Systems, Fort Mason Center, San

Francisco, California, USA.

Object Modeling Group, 2004. UML 2.0 Superstructure

Specification.

Object Modeling Group, 2003. OMG Unified Modeling

Language Specification, version 1.5.

Object Modeling Group, 2003. Object Management

Group. UML 2.0 OCL Specification.

Object Modeling Group, 2001. The UML Action

Semantics.

PROD 3.4, 2004. An advanced tool for efficient

reachability analysis, Laboratory for Theoretical

Computer Science, Helsinki University of

Technology, Espoo, Finland.

Roe, D., Broda, K., Russo, A., Mapping UML Models

incorporating OCL Constraints into Object-Z, Imperial

College Technical Report N°2003/9, 2003.

Royer,. J.-C., 2003. Temporal Logic Verifications for

UML, The Vending Machine Example. RSTI -

L'objet, 4

Rigorous Object-Oriented Methods

Workshop, vol. 9, no. 4, pp. 73-92.

Truong, N., Souquières, J., 2005. Verification of

behavioral elements of UML models using B. In

proceeding of 20th Annual ACM Symposium on

Applied Computing –SAC’05. New Mexico, USA.

Varro, D., 2002. A Formal Semantics of UML Statecharts

by Model Transition Systems, Proceedings of the 1st

International Conference on Graph Transformation,

Spain.

DATA FLOW FORMALIZATION

153