Comparison of Gene Selection and Machine Learning for

Tumor Classification

Qingzhong Liu

, Andrew H. Sung

1, 2

, Bernardete M. Ribeiro

Department of Computer Science

Institute for Complex Additive Systems Analysis

New Mexico Tech, Socorro, NM 87801, USA

Department of Informatics Engineering

University of Coimbra

3030-290 Coimbra, Portugal

Abstract.

Class prediction and feature selection are two learning tasks that are

strictly paired in the search of molecular profiles from microarray data. In this

paper, we apply the recursive gene selection proposed in our previous paper to

six types of micaroarray gene expression data for tumor classification. In com-

parison with other two well-known gene selections, SVM-RFE (Support Vector

Machine Recursive Feature Elimination) and T-test, our method outperforms

best. The kernel type and kernel parameters are critical to the classification per-

formances for the kernel classifiers. Our experiments indicate that RBF kernel

classifiers are pretty good under low feature dimensions; their performances in-

crease initially and then decrease as the feature dimension increases.

1 Introduction

Microarrays are capable of profiling the gene expression patterns of tens of thousands

of genes in a single experiment. DNA targets are arrayed onto glass slides (or mem-

branes) and explored with fluorescent or radioactively labeled probes [1]. Obtaining

gene expression data from cancerous tissues gives insight into the gene expression

variation of various tumor types, thus providing clues for cancer classification of

individual samples. One of the key challenges of microarray studies is to derive bio-

logical insights from the unprecedented quantities of data on gene expression pat-

terns. Partitioning genes into closely related groups has become an element of practi-

cally all analyses of microarray data [2]. However, identification of genes is faced

with many challenges. The main challenge is the overwhelming number of genes

compared to the smaller number of available training samples. In machine learning

terminology, these data sets have high dimension and small sample size. Many of

these genes are irrelevant to the distinction of samples. These irrelevant genes have a

negative effect on the accuracies of the classifier. Another challenge is that DNA

array data contain technical and biological noises. Thus, it is critical to identify a

subset of informative genes from a large data pool that will give higher classification

Liu Q., H. Sung A. and M. Ribeiro B. (2006).

Comparison of Gene Selection and Machine Learning for Tumor Classiﬁcation.

In Proceedings of the 2nd International Workshop on Biosignal Processing and Classiﬁcation, pages 13-22

DOI: 10.5220/0001219700130022

 SciTePress

accuracy.

Because DNA microarray data has high dimension and small samples, the gene

selection is very important to the classification accuracy. T-TEST [3] is one well-

known gene selection in DNA microarray analysis. It ranks the significant genes

according to the p-values. Unfortunately, it just considers the individual gene, not the

interaction of genes. And the problem probably is that we might end up with many

highly correlated genes. If there is a limit on the number of genes to choose we might

not be able to include all informative genes. The method in [4] is to retrieve groups of

similar genes, and apply a test-statistic to select genes of interest. SVM-RFE (Support

Vector Machine Recursive Feature Elimination) is another well-known gene selection

which refines the optimum feature set by using SVM in a wrapper approach [5].

Peng, Long and Ding [6] presents a feature selection to achieve the max-dependency,

max-relevance, and min-redundancy based on mutual information. Recently, a

scheme of gene selection based on recursive feature addition and similarity measures

between the chosen genes and the candidates [7]. In comparison with the well-known

gene selections, T-TEST and SVM-RFE using different classifiers, on the average,

the method of recursive gene selection is the best regarding the classification accu-

racy under different feature dimensions.

In this paper, we apply the three gene selections of recursive feature addition [7],

SVM-RFE [5] and T-test. We compare the

mean test accuracy and the highest test

accuracy under the highest train accuracy, and the highest test accuracy in the ex-

periments.

Additionally, we apply several learning classifiers to the experiments, and

compare the classification performances on the gene selections. Generally, in the

three gene selection, recursive gene addition performs the best; in the learning classi-

fiers, on the average, Nearest Mean Scale Classifier (NMSC) and kernel classifiers

with polynomial kernels have better classification accuracy than others. Under the

high feature dimensions, the classification performances of RBF kernel classifiers

decrease along with the increase of the feature dimension.

2 Recursive Feature Additions for Gene Selection

Liu and Sung [7] proposed a scheme of gene selection based on supervised learning

and similarity measure between chosen genes and candidates. We described it in brief

as follows:

1. Insignificant or noise microarray gene data is filtered out according to test-

statistical selection.

2. Each individual gene is ranked in the order from the highest classification accu-

racy to the lowest classification accuracy with some classifier.

3. The gene with the highest classification accuracy is chosen as the most important

feature, or the first feature. If there are many genes with the same highest classifica-

tion, the most important feature is set to the gene with the lowest p-value measured by

test-statistic. At this point the chosen feature set, G

, consists of the first feature, g

which corresponds to feature dimension one.

4. The N + 1 – dimension feature set, G

N+1

= { g

,…, g

, g

N+1

} is produced by

adding g

N+1

into the chosen N-dimension feature set, G

= { g

,…, g

}. The

choosing of the N+1

feature g

N+1

is described as follows.

Each gene g

(i ≠ 1, 2, …, N) outside of G

is added into G

; the classification ac-

curacy of each feature set G

+ {g

} is compared, the g

with the highest classifica-

tion accuracy is marked and put into the set of candidates, C. Generally, the set of

candidates consists of many genes, but only one gene in the set of candidates will be

the chosen. Three strategies are designed for choosing the g

N+1

The first strategy is to compare the individual classification accuracy of the candi-

dates. The candidates with the highest accuracy will be put into the final stunt; the

gene with the lowest p-value in the final stunt is chosen as the N+1

feature g

N+1

The second strategy is to measure the similarity of chosen genes and candidate

genes. Pearson’s correlation [19] between the chosen gene g

∈

, n = 1, 2…

N) and the candidate g

∈

C, c= 1,2 … m; m is the number of the elements in C.)

is calculated. The sum of the square of the correlation (SC) is calculated to measure

the relation, defined as follows:

SC(g

) =

∑

cor

n 1

, g

) (1)

Where, g

∈

C, g

∈

, n = 1, 2… N. The g

with the minimal value of SC(g

) is

chosen as g

N+1

The third strategy is to calculate the maximum value of the square of the correla-

tion (MC),

MC(g

) =

(cor

, g

) ), n = 1, 2… N. (2)

Where, g

∈

C, g

∈

. The g

with the minimum value of MC(g

) is chosen as

N+1

In the methods mentioned above, a feature is recursively added into the feature set

under the supervised learning. Similar to the name of SVM-RFE, we call the strate-

gies Classifier-Recursive Feature Addition (C-RFA), Classifier Minimal Sum of the

square of Correlation-Recursive Feature Addition (CMSC-RFA), Classifier Minimal

Maximal value of the square of Correlation-Recursive Feature Addition (CMMC-

RFA), respectively. For example, if the classifier is Naïve Bayes Classifier (NBC),

we record them NBC-RFA, NBCMSC-RFA, and NBCMMC-RFA, respectively.

3 Experiments

3.1 Data Sets

The following benchmark datasets are tested in our experiments. If the data source is

not mentioned, it is available at:

http://www.broad.mit.edu/cgi-bin/cancer/datasets.cgi.

1) The LEUKEMIA data set consists of two types of acute leukemia: 48 acute lym-

phoblastic leukemia (ALL) samples and 25 acute myeloblastic leukemia (AML)

samples, over 7129 probes from 6817 human genes. It was originally studied in the

paper [8].

2) The LYMPHOMA data set consists of 58 diffuse large B-cell lymphoma (DLBCL)

samples and 19 follicular lymphoma (FL) samples. It was studied in the paper [9].

The data file, lymphoma_8_lbc_fscc2_rn.res, and the class label file, lym-

phoma_8_lbc_fscc2.cls are used in our experiments for identifying DLBCL and

FL.

3) The PROSTATE data set in the paper [10] contains 52 prostate tumor samples and

50 non-tumor prostate samples.

4) The COLON data set in the paper [11] contains 62 samples collected from colon-

cancer patients. Among them, 40 tumor biopsies are from tumors and 22 normal

biopsies are from healthy parts of the colons of the same patients. 2000 genes were

selected based on the confidence in the measured expression levels. The data

source is available at:

http://microarray.princeton.edu/oncology/affydata/index.html.

5) Only dataset C in the dataset of Central Nervous System (CNS) embryonal tumor

[12] that is used to analyze the outcome of the treatment contains 60 patient sam-

ples, 21 are survivors who are alive after treatment and 39 are failures who suc-

cumbed to their diseases. There are 7129 genes.

6) Breast cancer dataset associated with the paper [13] contains 97 patient samples,

46 patients are relapse who had developed distance metastases within 5 years, and

51 patients are non-relapse who remained healthy from the distance after their ini-

tial diagnosis for interval of at least 5 years. The data source is available at:

http://www.rii.com/publications/2002/vantveer.htm.

3.2 Experimental Setup

Our experiments are described as follows:

1. The training samples are chosen from the datasets at random. The rest samples are

used for test. The ratio of training sample to test sample is 3:2 in the same class.

2. The gene selections, T-TEST, SVM-RFE, and the Recursive Feature Additions are

applied for gene selection based on the training samples. Different feature sets of

the gene expression data are produced under the feature dimension 1 to 50.

3. Several classifiers are applied to the feature sets extracted from test samples.

4. Repeat steps 1-3 30 times.

Although the results in [7] show that, regarding the average test accuracy in each

feature dimension, overall, the recursive gene addition performs best, the statistic for

evaluation is not enough. In our new experiments, the following statistics are meas-

ured to evaluate the performances of the gene selections.

(1) The average test accuracy under the condition that the associated train accuracy is

the highest in the experiments.

(2) The highest test accuracy under the condition that the associated train accuracy is

the highest in the experiments.

(3) The highest test accuracy in the experiments.

In our experiments, Naive Bayes Classifier (NBC) is applied for recursive gene

addition. The test classifiers are Nearest Mean Scale Classifier (NMSC), Kernel

Fisher Discriminant (KFD), Support Vector Machine (SVM), NBC, and uncorrelated

normal based quadratic Bayes Classifier that is recorded as UDC [14, 15, 16, 17, 18].

3.3 Comparison of Gene Selections

3.3.1 Comparison of the Average Test Accuracy and the Highest Test Accuracy

Under the Condition that the Associated Train Accuracy is the Highest

Generally, the feature set that is associated with the highest train accuracy is prone to

be treated as the final feature set. We compare the mean test accuracy and the highest

test accuracy under the condition that the associated train accuracy is the highest.

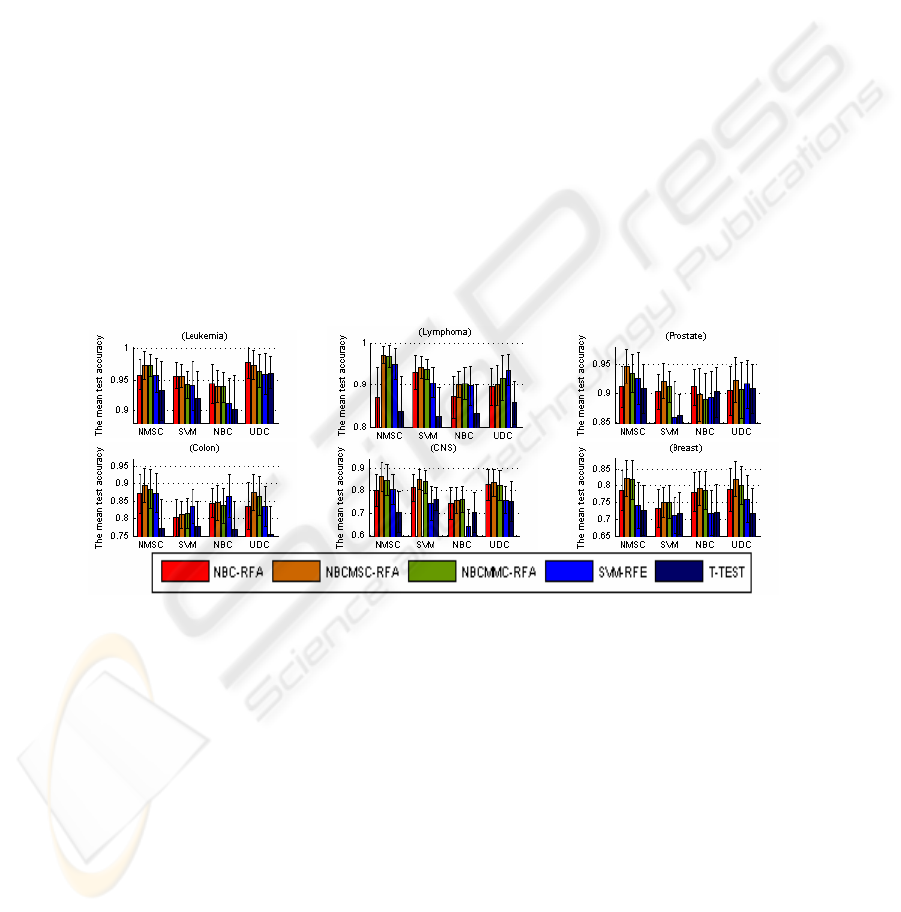
Fig. 1 lists the average test accuracy associated with the highest train accuracy. Fig.

1 indicates that, NBCMSC-RFA is the best, followed by NBCMMC-RFA, SVM-RFE

and NBC-RFA. On the average, T-TEST is not better than others. Fig. 2 lists the

highest test accuracy associated with the highest train accuracy in the experiments.

Fig. 2 also indicates that NBCMSC-RFA is the best, followed by NBCMMC-RFA,

SVM-RFE, and NBC-RFA. T-TEST is the least one. Because of the space limit, the

classification with the use of KFD is not shown in the figures.

Fig. 1. The mean test accuracy associated with the highest train accuracy. In the 24 groups,

NBCMSC-RFA is the best in 16 groups; NBCMMC-RFA is the best in the 4 groups (applying

NMSC to Leukemia, NBC to Lymphoma and CNS, and SVM to Breast); SVM-RFE is the best

in the 3 groups (applying UDC to Lymphoma, SVM to Colon, and NBC to Colon); and NBC-

RFA is the best in 3 groups (applying NBC and UDC to Leukemia, NBC to prostate). The

highest test accuracy is obtained by recursive gene selection based on the correlation measures

in the five types of cancer data (Lymphoma, Prostate, Colon, CNS, and Breast) and NBC-RFA

gains the highest test accuracy for Leukemia data classification.

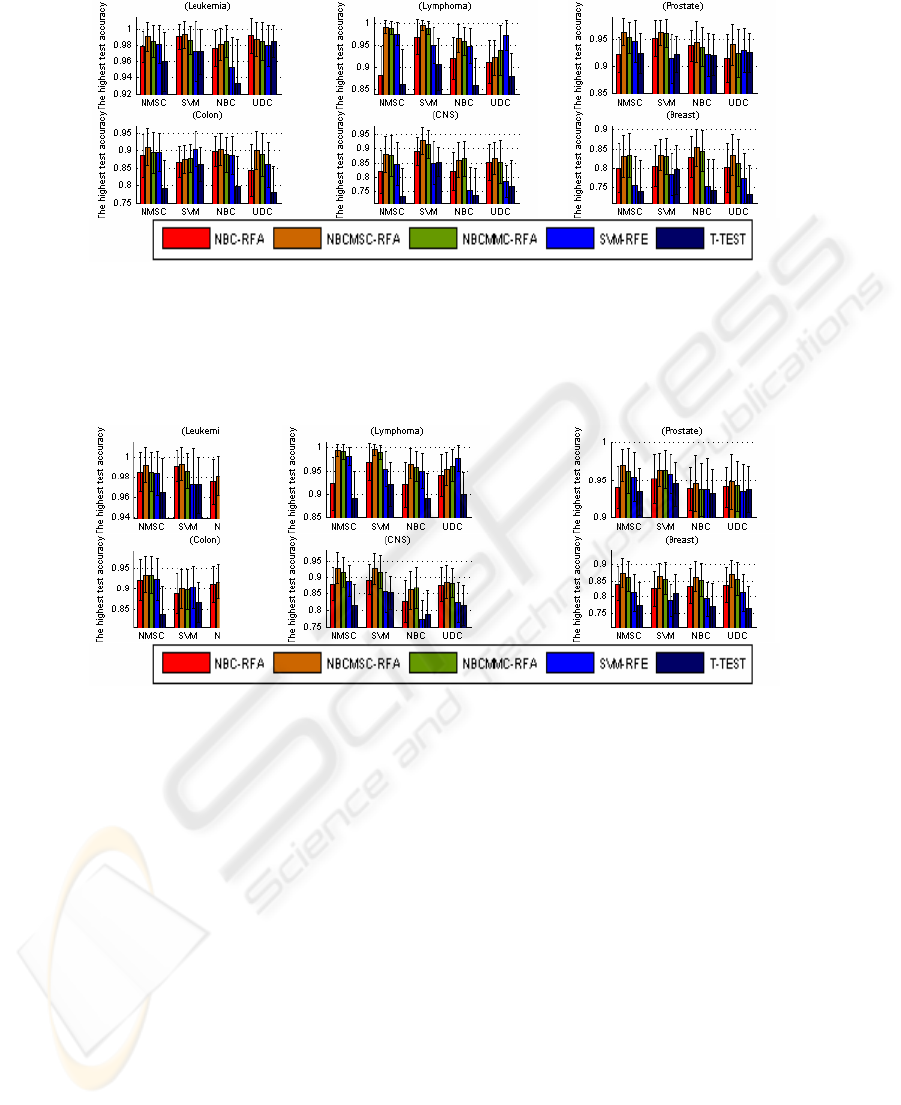
Fig. 2. The highest test accuracy associated with the highest train accuracy. In the 24 groups,

NBCMSC-RFA is the best in the 18 groups; NBCMMC-RFA is the best in the 3 groups (apply-

ing NBC to Leukemia and CNS, NMSC to Breast); SVM-RFE outperforms others in 2 groups

(applying UDC to Lymphoma, and SVM to Colon). NBC-RFA and T-TEST gain no champi-

onship. For the six types of cancer data, all the highest test accuracy is obtained by recursive

gene selection based on the correlation measures.

Fig. 3. The highest test accuracy under the feature dimension 1 to 5. In the 24 groups,

NBCMSC-RFA is the best in 19 groups; NBCMMC-RFA is the best in 3 groups; SVM-RFE is

the best in 2 groups (applying UDC to Lymphoma, SVM to Colon); NBC-RFA is the best in 1

group; and T-TEST gains no championship. In the test for each type of cancer data, all the

highest test accuracy is obtained by recursive gene selection based on the correlation measures

3.3.2 Comparison of the Highest Test Accuracy

Fig. 3 lists the highest test accuracy, regardless of the train accuracy. In the 24

groups, NBCMSC-RFA is the best in 19 groups; NBCMMC-RFA is the best in 3

groups; SVM-RFE is the best in 2 groups (applying UDC to Lymphoma, SVM to

Colon); NBC-RFA is the best in 1 group; and T-TEST gains no championship. In the

test for each type of cancer data, all the highest test accuracy is obtained by recursive

gene selection based on the correlation measures. It also indicates that NBCMSC-

RFA is the best, followed by NBCMMC-RFA, SVM-RFE, and NBC-RFA. T-TEST

is the worst in comparison with other gene selections. On the average, regarding

different classifiers, Figures 1 to 3 indicate that NMSC and SVM outperform others.

3.4 Comparison of Kernel Classifiers

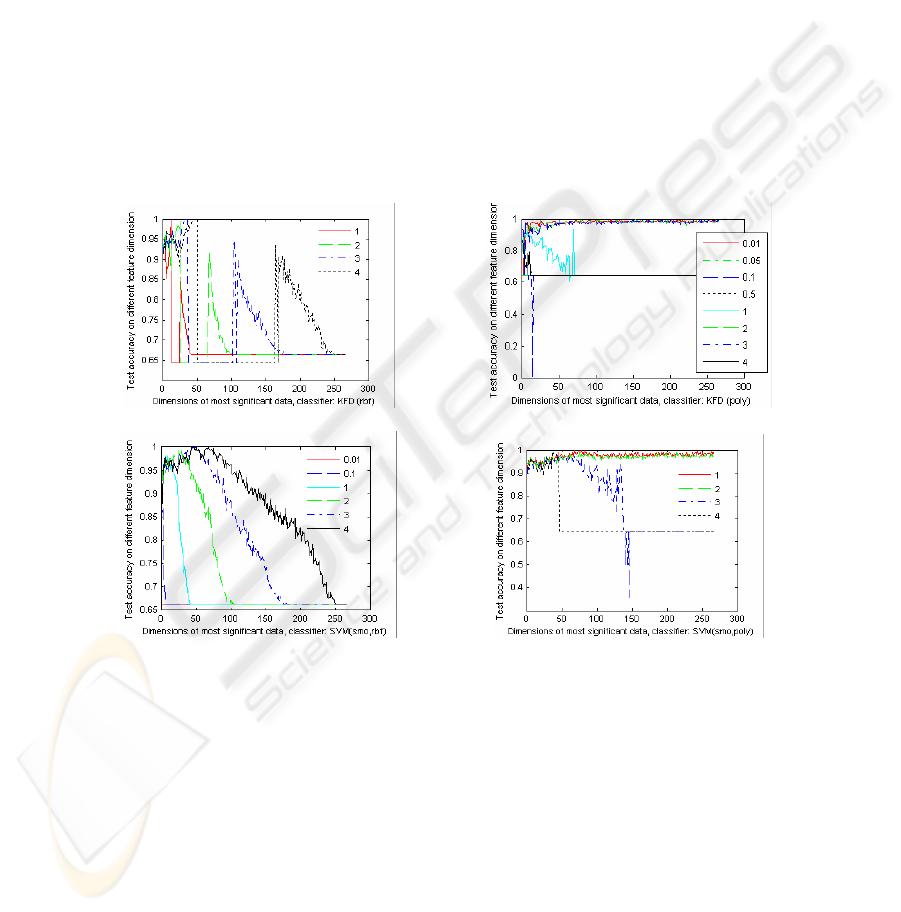
Fig.4 - Fig. 6 compares the performances of the kernel classifiers, KFD and SVM

with different RBF kernel and POLY kernel for the gene selection of T-TEST under

different feature dimensions. Where, SMO (Sequential Minimal Optimization for

binary SVM with L1-soft margin) is applied to train model. The legends marked in

the Figures are the kernel arguments. The regularization of SVM is 10, and regulari-

zation of KFD criterion is 0.0001. Fig.4 - Fig. 6 indicates that the kernel type and the

kernel parameters are very important to the classification accuracy. They show that

the performances of the kernel classifiers, KFD and SVM with a RBF kernel will

increase initially as the feature dimension increases, and then decrease when the fea-

ture dimension increases continually. While the recognition performances of the

POLY kernel classifiers improve as feature dimension increases. The exception

shown in Fig. 4 (a) are resulted from the bad train models.

(a)

(b)

(c)

(d)

Fig. 4. The test classification of KFD with different RBF kernels (a) and POLY kernels (b) and

SVM with different RBF (c) and POLY (d) kernels for LEUKEMIA.

(a)

(b)

(c)

(d)

Fig. 5. The test classification of KFD with different RBF kernels (a) and POLY kernels (b) and

SVM with different RBF (c) and POLY (d) kernels for LYMPHOMA.

(a)

(b)

(c)

(d)

Fig. 6. The test classification of KFD with different RBF kernels (a) and POLY kernels (b) and

SVM with different RBF (c) and POLY (d) kernels for PROSTATE.

(a)

(b)

Fig. 7. The train accuracy of SVM with RBF kernels (a) and KFD with RBF kernels (b) for

PROSTATE.

Fig. 7 shows the train classification accuracy of the KFD and SVM with RBF ker-

nels. It show that the train accuracy values of the RBF kernels are pretty high, almost

100%. We infer that, from the difference between the train accuracy (Fig. 7) and the

test accuracy (Fig. 6 (a), Fig. 6(c)), in a high feature dimension, even the training

error (or empirical risk) is very low, does not imply a small expected value of the test

error (called risk) [14, 20].

4 Conclusions

On the average, the recursive feature addition based on supervised learning and corre-

lation measures is better than the well-known gene selection methods of SVM-RFE

and T-TEST regarding the

mean test accuracy and the highest test accuracy under the

highest train accuracy, and the highest test accuracy in the experiments.

Regarding the classifiers in our experiments, on the average, NMSC and SVM out-

perform others in the majority tests. And the kernel type and kernel parameters are

important to the classification performances of the kernel classifiers. The RBF kernel

classifiers are pretty good under low feature dimensions; their performances increase

initially and then decrease as the feature dimension increases. The classification per-

formances of the POLY kernel classifiers improve as the feature dimension increase.

Acknowledgements

Partial support for this research received from ICASA (Institute for Complex Addi-

tive Systems Analysis, a division of New Mexico Tech) is gratefully acknowledged.

References

1. Brown,P. and Botstein,D. (1999) Exploring the New World of the Genome with DNA

Microarrays. Nature Genetics Supplement, 21, 33-37.

2. Quackenbush,J. (2001) Computational Analysis of Microarray Data, Nature Rev. Genetic,

2, 418-427.

3. Armitage,P. and Berry,G. (1994) Statistical Methods in Medical Research, Blackwell.

4. Jaeger,J., Sengupta,R. and Ruzzo,W.(2003) Improved Gene Selection for Classification of

Microarray, Pacific Symposium on Biocomputing 8, 53-64.

5. Guyon,I, Weston, J., Barnhill,S. and Vapnik,V. (2002) Gene Selection for Cancer Classifi-

cation using Support Vector Machines, Machine Learning, 46(1-3), 389-422.

6. Peng,H, Long,F. and Ding, C. (2005) Feature selection based on mutual information: crite-

ria of max-dependency, max-relevance, and min-redundancy, IEEE Trans. on Pattern

Analysis and Machine Intelligence, 27(8),1226-1238.

7. Liu,Q. and Sung,A.H. (2006) Recursive Feature Addition for Gene Selection, Proc. of

IEEE - IJCNN 2006, Vancouver, Canada.

8. Golub, T. et al. (1999) Molecular Classification of Cancer: Class Discovery and Class

Prediction by Gene Expression, Science, 286, 531-537.

9. Shipp,M. et al. (2002) Diffuse Large B-Cell Lymphoma Outcome Prediction by Gene

Expression Profiling and Supervised Machine Learning, Nature Medicine, 8(1), 68-74.

10. Singh,D. et al. (2002) Gene Expression Correlates of Clinical Prostate Cancer Behavior,

Cancer Cell, 1(2), 227-235.

11. Alon,U. et al. (1999) Broad Patterns of Gene Expression Revealed by Clustering Analysis

of Tumor and Normal Colon Tissues Probed by Oligonucleotide Arrays, Proc. Natl.

Acad.. Sci. USA, Cell Biology, 96, 6745-6750.

12. Pomeroy,S.L. et al. (2002) Prediction of Central Nervous System Embryonal Tumor

Outcome based on Gene Expression, Letters to Nature, Nature, 415, 436-442.

13. Van,L.J. et al.(2002) Gene expression profiling predicts clinical outcome of breast cancer,

Letters to Nature, Nature, 415, 530-536.

14. Vapnik,V. (1998) Statistical Learning Theory, John Wiley.

15. Schlesinger,M. and Hlavac,V. (2002) Ten Lectures on Statistical and Structural Pattern

Recognition, Kluwer Academic Publishers.

16. Heijden,F., Duin,R., Ridder,D. and Tax,D. (2004) Classification, Parameter Estimation

and State Estimation, John Wiley.

17. Taylor,J. and Cristianini,N. (2004) Kernel Methods for Pattern Analysis, Cambridge

University Press.

18. Webb,A. (2002) Statistical Pattern Recognition, John Wiley & Sons, New York.

19. Tan,P., Steinbach,M. and Kumar,V. (2005) Introduction to Data Mining, Addison-

Wesley, 76-79.

20. Scholkopf,B., Guyon,I., Weston,J. (2003) Statistical Learning and Kernel Methods in

Bioinformatics, Artificial Intelligence and Heuristic Methods in Bioinformatics, P. Fras-

coin and R. Shamir (Eds.) IOS press, 2003