
A GAIN-SCHEDULING APPROACH FOR
AIRSHIP PATH-TRACKING
Alexandra Moutinho
IDMEC - IST
Instituto Superior T
´
ecnico, Av. Rovisco Pais, 1047-001 Lisbon, Portugal
Jos
´
e Raul Azinheira
IDMEC - IST
Instituto Superior T
´
ecnico, Av. Rovisco Pais, 1047-001 Lisbon, Portugal
Keywords:
UAV, gain-scheduling, path-tracking, optimal control, airship.
Abstract:
In this paper a gain scheduled optimal controller is designed to solve the path-tracking problem of an airship.
The control law is obtained from a coupled linear model of the airship that allows to control the longitudinal
and lateral motions simultaneously. Due to the importance of taking into account wind effects, which are
rather important due to the airship large volume, the wind is included in the kinematics, and the dynamics
is expressed as function of the air velocity. Two examples are presented with the inclusion of wind, one
considering a constant wind input and the other considering in addition a 3D turbulent gust, demonstrating the
effectiveness of this single controller tracking a reference path over the entire flight envelope.
1 INTRODUCTION
The range of civilian and military applications of Un-
manned Aerial Vehicles (UAV’s) is driving the growth
of the rapidly changing market for UAVs globally.
The list of applications and opportunities in this do-
main is already large and is continually growing.
Among these are inspection oriented applications that
cover different areas such as mineral and archaeo-
logic prospecting, land use surveys in rural and urban
regions, inspection of man-made structures such as
pipelines, power transmission lines, dams and roads.
Most of the applications cited above have profiles
that require maneuverable low altitude, low speed air-
borne data gathering platforms. The vehicle should
also be able to hover above an observation target,
present extended airborne capabilities for long dura-
tion studies, take-off and land vertically without the
need of runway infrastructures, have a large payload
to weight ratio, among other requisites. For this sce-
nario, lighter-than-air (LTA) vehicles, like airships,
are often better suited than balloons, airplanes and he-
licopters (Elfes et al., 1998), mainly because: they de-
rive the largest part of their lift from aerostatic, rather
than aerodynamic forces; they are safer and, in case
of failure, present a graceful degradation; they are in-
trinsically of higher stability than other platforms.
For all its advantages, airships are being chosen
as platform to a variety of applications. Some ex-
amples are demining
1
, fire detection (Merino et al.,
2005), emergency management (Rao et al., 2005), tar-
get search (Xia and Corbett, 2005) and even explo-
ration of planetary bodies (Elfes et al., 2003).
In some cases, the airship is remotely maneuvered,
but a wider range of applications is achievable with
unmanned autonomous airships, which requires an ef-
fective control of the robot behavior. Like other aerial
vehicles, the airship dynamics is highly nonlinear. It
mostly varies with the relative airspeed, which influ-
ences both acting forces as well as actuators authority.
In flight control design, it is an established practice to
base the controller design in a linear description of
the system, obtained assuming the motion of the aer-
ial vehicle is constrained to small perturbations about
a trimmed equilibrium flight condition (Stevens and
Lewis, 1992). For instance, Hygounenc and Sou
`
eres
consider linear decoupled models for the longitudinal
and lateral motions. The vertical movement is reg-
ulated using a Lyapunov based approach, while the
horizontal path-following problem is independently
solved with a PI controller (Hygounenc and Sou
`
eres,
2003). Xia and Corbett apply the slidding mode tech-
nique to the linear decoupled systems in order to ob-
tain a cooperative control system for two blimps (Xia
and Corbett, 2005). Complementing the linear model
of the airship with the vector of visual signals, Sil-
veira et al. report a line following visual servo control
1
www.mineseeker.com
82
Moutinho A. and Azinheira J. (2006).
A GAIN-SCHEDULING APPROACH FOR AIRSHIP PATH-TRACKING.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 82-88
DOI: 10.5220/0001219800820088
Copyright
c
SciTePress

scheme with a PID structure (Silveira et al., 2003).
Although using different control methodologies,
the above references all implicitly use the gain
scheduling approach (
˚
Astr
¨
om and Wittenmark, 1989;
Khalil, 2000a), the prevailing flight control design
methodology nowadays (Rugh and Shamma, 2000).
As mentioned, the linear model of the system is an ap-
proximation only valid for small perturbations around
an equilibrium condition, which leads to the necessity
of repeating the linearization process for several trim
points over the desired operation range.
In this paper a gain scheduled optimal controller is
designed to solve the path-tracking problem for the
airship of the Aurora (Autonomous Unmanned Re-
mote mOnitoring Robotic Airship) project (de Paiva
et al., 2006). The control law is obtained from a cou-
pled linear model of the airship that allows to control
the longitudinal and lateral motions simultaneously.
Due to the importance of taking into account wind ef-
fects, which are rather important due to the airship
large volume, the wind is included in the kinemat-
ics, and the dynamics is expressed as function of the
air velocity. The designed controller has been tested
exhaustively in simulation environment prior to real
implementation, and effective results have been ob-
tained covering the entire flight envelope with the sin-
gle controller. We present here two cases concern-
ing the same reference tracking: a nominal case and
a case considering realistic wind disturbances, which
the airship platform is supposed to face during its nor-
mal operation.
In this article we start by describing the Aurora air-
ship platform, followed by the definition of the model
used in the control design (§ 2). In § 4 we propose an
optimal gain scheduled control, applied to the path-
tracking problem in § 3. So as to illustrate the valu-
able results obtained, in § 5 we show examples of the
proposed control acting over the entire flight envelope
in the presence of wind disturbances. Finally, conclu-
sions are summarized in § 6.
2 AIRSHIP DESCRIPTION
2.1 Airship Platform
In this section we briefly describe the airship platform
of the Aurora project (de Paiva et al., 2006).
The LTA robotic prototype has been built as an evo-
lution of the Airspeed Airships’ AS800. It is a non-
rigid airship with 10.5m long, 3.0m diameter, and
34m
3
of volume, whose payload capacity is approxi-
mately 10kg and maximum speed is around 50km/h
(see fig. 1). As main control actuators, the airship has:
i) four deflection surfaces at the tail in the ’×’ con-
figuration; ii) the thrust provided by two propellers
driven by two-stroke engines; iii) the vectoring of this
propulsion group.
Figure 1: The Aurora airship.
The airship system state variables are measured by
a GPS with differential correction, an inertial mea-
surement unit and a wind sensor.
2.2 Airship Model
Consider an underactuated airship modeled as a rigid
body subject to forces and torques. Let {i} repre-
sent the inertial frame (which, for simplicity, is con-
sidered coincident with the geographical north-east-
down (NED) frame), {l} be the body-fixed coordinate
frame whose origin is located in the airship center of
volume, and S(Φ) ∈ SO(3) := {S ∈ R
3×3
: SS
′
=
I, det(S) = +1} is the rotation matrix from {i} to
{l} frame, and where Φ ∈ R
3×1
is the attitude of {l}
in relation to {i} expressed as the Euler angles roll φ,
pitch θ and yaw ψ.
The airship dynamic equations of motion (Azin-
heira et al., 2002) may be condensed in the form
M
˙
V = −Ω
6
MV + ESg + F
a
+ f(U
a
, V
t
) (1)
˙
P = JV (2)
where V = [v
′
, ω
′
]
′
∈ R
6×1
includes the airship lin-
ear and angular velocities relative to {i} expressed in
{l}, P = [p
′
, Φ
′
]
′
∈ R
6×1
contains the airship carte-
sian and angular positions expressed in the {i} frame,
J = diag{S
′
, R} ∈ R
6×6
, R = R(Φ) ∈ R
3×3
is a
coefficient matrix, and M ∈ R
6×6
is the symmetric
inertia matrix. Ω
6
= diag{Ω(ω), Ω(ω)} ∈ R
6×6
,
Ω(ω) ∈ R
3×3
is the skew-symmetric matrix equiva-
lent to the cross-product ω×, E ∈ R
6×3
is the gravity
matrix input, and g ∈ R
3×1
represents the gravity ac-
celeration in the {i} frame. F
a
∈ R
6×1
stands for the
aerodynamic forces and moments.
The input forces and torques f(U
a
, V
t
) ∈ R
6×1
are
a nonlinear function of the airship airspeed V
t
and of
the actuators input U
a
∈ R
6×1
, which includes the
elevator δ
e
, the total left and right engines thrust X
T
,
the engines vectoring angle δ
v
, and the rudder δ
r
(see
figure 2).
A GAIN-SCHEDULING APPROACH FOR AIRSHIP PATH-TRACKING
83

−
X
T
δ
e
δ
v
δ
r
+
+
−
+
−
Figure 2: Airship actuators.
2.2.1 Inclusion of Wind
We assume that the inertial wind velocity vector
˙
p
w
= S
′
v
w
is constant over a region much larger
than the size of the airship. This means we do not
consider wind shearing effects and torques exerted on
the airship (ω
w
= 0).
The velocity of the airship center of volume with
respect to the air represented in the {l} frame is given
by
v
a
= v − v
w
(3)
In order to include the wind influence in the airship
equations of motion, the wind components must be
supplied as inputs. Then v
a
, rather than v, must be
used in the calculation of the aerodynamic forces and
moments. The airship dynamics and kinematics can
then be rewritten as
˙
V
a
= M
−1
[−Ω
6
MV
a
+ ESg + F
a
+ f(U
a
)]
(4)
˙
P = JV
a
+ S
′
V
w
(5)
with V
a
= [v
′
a
, ω
′
]
′
and V
w
= [v
′
w
, 0]
′
.
As mentioned before, the wind must be provided
as input to equations (4) and (5). Since the wind is
not directly measurable, we will need to compute an
estimate. Knowing that
v
a
=
"
V
t
cos(α) cos(β)
V
t
sin(β)
V
t
sin(α) cos(β)
#
(6)
where the airspeed V
t
, the angle of attack α and the
sideslip angle β are measurable quantities, we can
compute the wind velocity vector v
w
using equation
(3).
2.2.2 Linear Model
The complexity of the nonlinear dynamic equations
justifies the search for a linear simplified version, also
necessary if to use the gain-scheduling approach.
The linearization of the dynamic equations (4)-(5)
is made for trimmed conditions around equilibrium,
which is commonly an horizontal straight flight, with-
out wind incidence.
Considering only the dynamic or perturbed part,
and for the conditions stated, the motion equations
are written for a perturbation vector x of the states
around the equilibrium value X
o
, and the perturbed
input u around the trimmed value U
o
, resulting in the
matricial dynamic equation:
˙
x = Ax + Bu (7)
in the absence of disturbances (deterministic case).
The linearized model (7), i.e., the dynamic and in-
put matrices A and B, depend on the trim point cho-
sen for the linearization, and in particular of the cho-
sen airspeed V
t
o
(we consider here low altitude flight,
where the altitude variation is insufficient to signifi-
cantly change the envelope pressure). The existence
of a constant wind component is also to be consid-
ered.
In flight control, and as a result of the applica-
tion of the small perturbations theory, two indepen-
dent (decoupled) linear models are usually obtained,
corresponding to the lateral and longitudinal mo-
tions (Stevens and Lewis, 1992). Here, we chose to
work with a single linear model, which allows us to
design a single controller for the lateral and longitu-
dinal movements.
Considering that all variables now correspond to
the perturbation term, the state and input vectors of
the dynamics equation (7) are x = [v
′
a
, ω
′
, p
′
, Φ
′
]
′
and u = [δ
e
, X
T
, δ
v
, δ
r
]
′
.
3 PATH-TRACKING PROBLEM
Let us start by define the vehicle mission: to force the
output to follow a reference signal, a given function
of time, and to drive to zero the tracking error:
e(t) = y(t) − y
r
(t) (8)
This path-tracking problem differs from the path-
following one by the fact that the path reference is
time dependent.
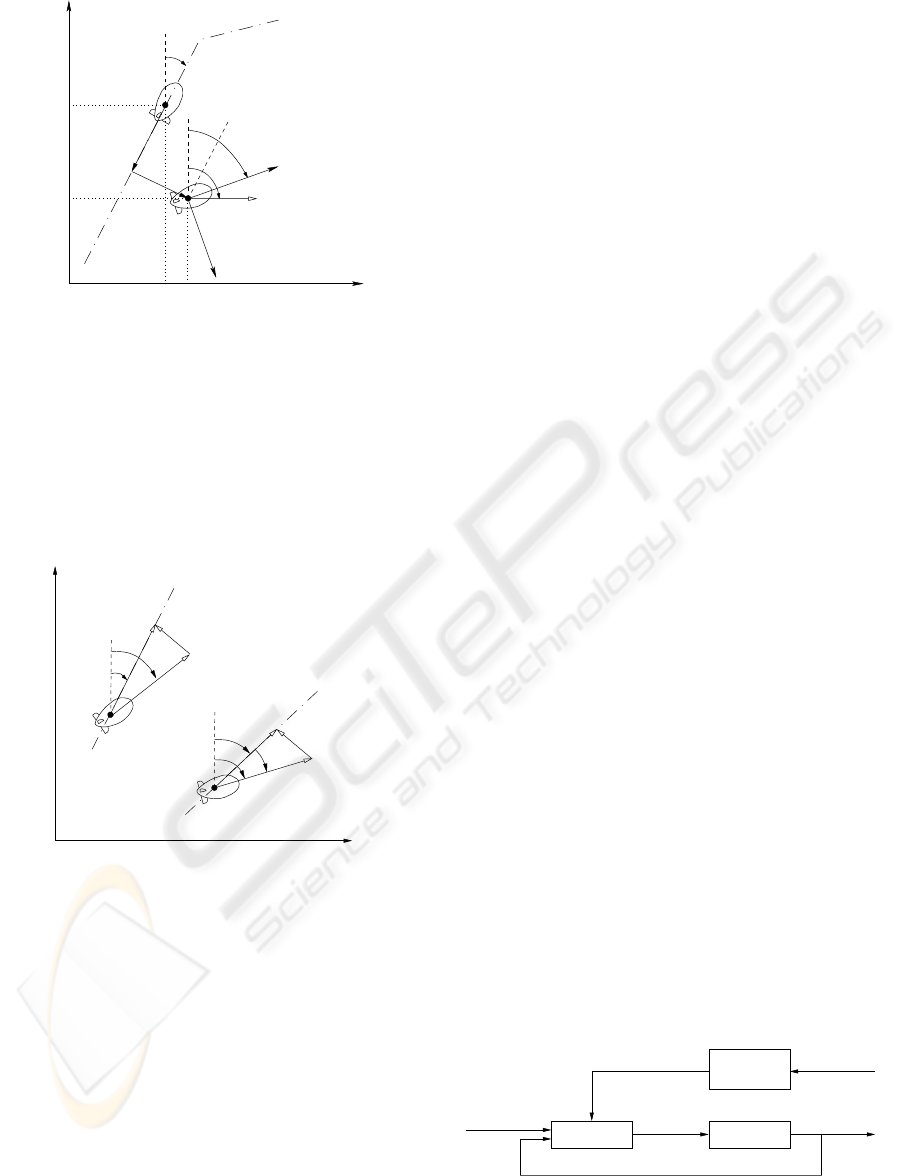
We define here the cartesian position error e
p
=
[η, δ, γ]
′
as expressed in the reference path frame and
computed by (see fig. 3)
e
p
= S(Φ
r
)(p − p
r
) (9)
The reference path attitude Φ
r
= [φ
r
, θ
r
, ψ
r
]
′
is
obtained considering φ
r
= 0, and θ
r
and ψ
r
as the
angles the reference trajectory does respectively with
the horizontal plane, and the north direction.
The attitude error is the difference between the air-
ship and reference attitudes:
e
Φ
= Φ − Φ
a
r
(10)
ICINCO 2006 - ROBOTICS AND AUTOMATION
84
˙
p
E
r
E y
i
x
i
p
r
ψ
r
ψ
N
N
r
y
l
reference
x
l
δ
p
η
λ
path
Figure 3: Position errors definition (2D).
If we were not taking into account the wind input,
Φ
a
r
≡ Φ
r
. However, due to the sideslip, the airship
orients itself with the relative air direction (see fig. 4).
Therefore, the attitude reference Φ
a
r
corresponds to
the estimated attitude of the reference velocity influ-
enced by the wind,
ˆ
˙
p
a
r
.
ψ
a
r
reference
position
position
actual
x
i
y
i
β
ˆ
˙
p
w
ˆ
˙
p
ar
˙
p
r
ψ
r
˙
p
a
˙
p
ψ
a
ˆ
˙
p
w
λ
Figure 4: Reference heading estimation (2D).
We compute the reference attitude Φ
a
r
following
these three steps:
1. with the airship inertial velocity
˙
p, its attitude Φ
and the aerodynamic variables V
t
, β and α (all
measured variables), estimate the wind inertial ve-
locity vector
ˆ
˙
p
w
using equations (6) and (3), and
knowing that
˙
p = S(Φ)
′
v;
2. compute the velocity in the aerodynamic frame
ˆ
˙
p
a
r
as the inertial vectors difference between the air-
ship reference velocity
˙
p
r
and the wind velocity
estimation
ˆ
˙
p
w
;
3. consider φ
a
r
= 0, and θ
a
r
and ψ
a
r
as the angles
ˆ
˙
p
a
r
does respectively with the horizontal plane,
and the north direction.
The objective of the control design proposed in the
next section is then to drive to zero the errors given by
equations (9) and (10).
4 GAIN-SCHEDULING
The linearized system model (7) presented before is
only valid for small regions around trim conditions.
This reveals the basic limitation of the design via the
linearization approach, the fact that the controller is
guaranteed to work only in the neighborhood of a sin-
gle operating (equilibrium) point. The gain schedul-
ing technique (Khalil, 2000b) addressed here allows
to extend the validity of the linearization approach to
a range of operating points, in this case over the entire
flight envelope.
It is sometimes possible to find auxiliary variables
that correlate well with the changes in the process dy-
namics. In the airship case, these variables mostly
correspond to the airspeed V
t
and altitude h. Still, the
altitude influence may be disregarded for low altitude
flights where the envelope pressure is kept practically
constant. The airspeed, however, has a major influ-
ence over the airship behavior. It not only determines
the magnitude of the aerodynamic forces acting on
the airship, but also rules the influence of the actua-
tors on the airship motion. As example, the action of
the control surfaces, corresponding to the standard in-
puts δ
e
and δ
r
, is a function of the dynamic pressure
and varies as the square of the airspeed (Stevens and
Lewis, 1992), which leads to a reduced authority of
these actuators when flying at low airspeeds.
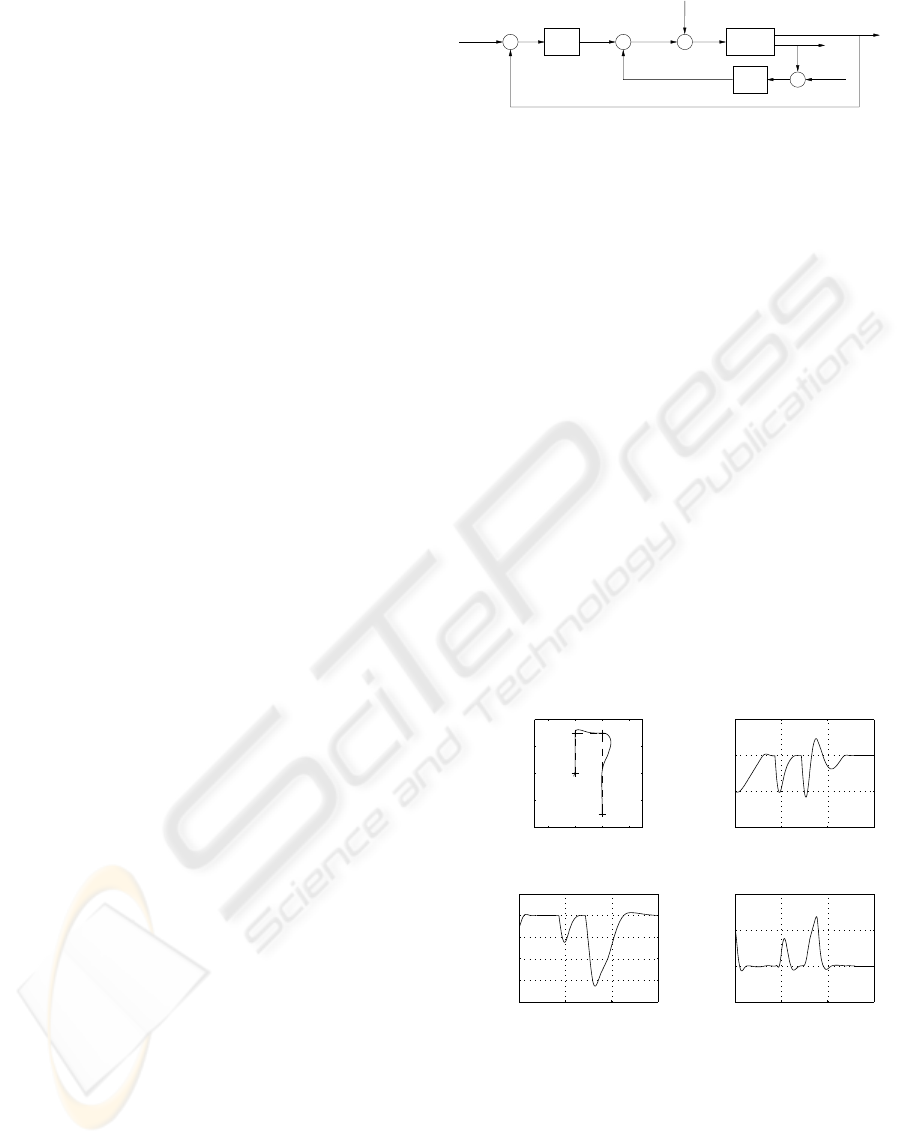
Obtaining a linearized system at several equilib-
rium points, followed by the design of a linear feed-
back controller for each point, and implementation of
the resulting family of linear controllers as a single
controller whose parameters are changed by monitor-
ing the scheduling variable, results in a gain sched-
uled controller (see figure 5). This controller is ex-
pected to maintain the stability and performance of
the linear systems as long as the design models are
reasonable representations of the system dynamics
and as long as the scheduling variable varies ”slowly”.
command
output
u y
signal
regulator
control
process
gain
schedule
regulator
parameters
operating
condition
signal
Figure 5: Gain-scheduling block diagram.
A GAIN-SCHEDULING APPROACH FOR AIRSHIP PATH-TRACKING
85
4.1 Optimal Control
Here we discuss the design of a servo control sys-
tem whose purpose is to keep the tracking error small,
while the airship flight condition is kept near the equi-
librium state.
Consider the linear system defined by equation (7),
assume the complete state x is measurable, and that
the output variable
y = Cx (11)
is to track a reference input y
r
. The tracking error is
then defined as
e = y − y
r
(12)
Considering that the model represents the deviations
from an equilibrium state X
o
, it is required that the
state variables x
c
that do not form the output vector
be kept null, in order to have X
c
= X
c
o
.
The admissible control is a proportional output
feedback of the form
u = K
y
e − K
c
x
c
= −Kz (13)
where z = [e
′
, x
′
c
]
′
and K = [K
y
K
c
].
We use an optimal Linear Quadratic regulator to
obtain the control effort (13), that results from the
minimization of the cost function
J =
Z
∞
0
(z
′
Qz + u
′
Ru)dt (14)
subject to the system dynamics (7). The state and con-
trol weighting matrices Q ≥ 0 and R > 0 are the
designer tools to balance the state errors z against the
control effort u. In the airship control case, the con-
trol weighting matrix R is a specially important tool
in the sense that it allows the designer to change the
control effort of the different actuators over the flight
envelope.
The gain matrix K is obtained from
K = R
−1
B
′
P (15)
solving first the algebraic Riccati equation for the pos-
itive definite matrix P
PA + A
′
P − PBR
−1
B
′
P + Q = 0 (16)
The actuators request
U = U
o
+ u (17)
has to be computed for each linearized model, which
means the procedure has to be repeated for different
airspeeds. Figure 6 illustrates the closed-loop dia-
gram for a determined equilibrium condition.
X
c
o
−
+
−
airship
X
c
Y
K
y
Σ
K
c
Σ
ΣΣ
+
−
u
+
U
o
Y
r
+
U
+
Figure 6: Linear control block diagram.
5 SIMULATION RESULTS
From the various simulations carried out, two exam-
ples are illustrated here concerning the same reference
tracking: a nominal case with constant wind input and
a case considering realistic wind disturbances, i.e.,
with an aleatoric component, which the airship plat-
form is supposed to face during its normal operation.
In both cases the airship is to follow a reference
path p
r
(t) at constant altitude h
r
= −D
r
= 50m,
starting deviated from the initial position at p
i
=
[−20, −10, −45]m and with the initial orientation
Φ
i
= [10, 10, 10]deg.
5.1 Nominal Case
This nominal case considers a constant wind input
of 4m/s coming from north. The airship horizontal
north-east trajectory with the correction from the ini-
tial deviation point and the cartesian position errors
e
p
= [η, δ, γ] are shown in figure 7.
East [m]
North [m]
Time [s]
η [m]
Time [s]
δ [m]
Time [s]
γ [deg]
0 50 100
150
0
50 100 150
0 50 100 150-200
0
200
400
-5
0
5
10
-80
-60
-40
-20
0
20
-40
-20
0
20
-400
-200
0
200
400
Figure 7: Nominal case: north-east trajectory (reference -
dashed, output - solid), and position errors: longitudinal η,
lateral δ and altitude γ.
After the initial deviation is corrected, the airship
position errors stabilize to zero after passing the ref-
erence path corners.
So as to avoid saturation of the thrusters when the
controller is correcting the airship position, the longi-
ICINCO 2006 - ROBOTICS AND AUTOMATION
86

tudinal position error η was limited. This can be no-
ticed by the constant rate at which the north position
is corrected (η curve in fig. 7).
5.2 Realistic Case
In order to exemplify the controller robustness when
in the presence of disturbances, further simulation
tests included a 3D turbulent gust (simulated here by
a Dryden model) with an intensity of 3m/s in addi-
tion to a constant wind blowing at 4m/s from north.
The remaining setup values were the same used in the
previous case.
Figure 8 shows the horizontal north-east trajectory
and the cartesian position errors e
p
= [η, δ, γ]. The
airship behavior is similar to the nominal case, with
the turbulent gust noticeable by the curves oscillation.
Again, the position errors are corrected to zero, hav-
ing the longitudinal error η been limited to avoid the
thrusters saturation.
East [m]
North [m]
Time [s]
η [m]
Time [s]
δ [m]
Time [s]
γ [deg]
0 50 100
150
0
50 100 150
0 50 100 150-200
0
200
400
-5
0
5
10
-80
-60
-40
-20
0
20
-40
-20
0
20
-400
-200
0
200
400
Figure 8: Realistic case: north-east trajectory (reference -
dashed, output - solid), and position errors: longitudinal η,
lateral δ and altitude γ.
The evolution of the airspeed V
t
, represented in fig-
ure 9, defines the variations of the linear model used
in the control design. The spam of the airspeed val-
ues over the flight envelope, between 2 and 12m/s,
is easily seen. This implies not only that the airship
dynamics suffer a severe alteration, but also the actu-
ators authority varies enormously. This can be con-
firmed comparing the airspeed curve with the graph-
ics of the actuators input (elevator δ
e
, total thrust X
T
,
vectoring angle δ
v
and rudder δ
r
) represented in fig-
ure 10.
Mostly we can observe the vectoring angle δ
v
change between 0deg for aerodynamic flight, and
90deg at low airspeeds.
The sideslip angle β is also represented in figure 9.
We can observe that its value oscillates around zero
Time [s]
V
t
[m/s]
Time [s]
β [deg]
0
50
100
150
0
50 100 150
-20
-10
0
10
0
6
12
Figure 9: Realistic case: airspeed V
t
and sideslip angle β.
Time [s]
δ
e
[deg]
Time [s]
X
T
[N]
Time [s]
δ
v
[deg]
Time [s]
δ
r
[deg]
0 50 100
150
0
50 100 150
0 50 100 1500
50
100
150
-25
0
25
-50
0
50
100
150
0
50
100
-20
-10
0
10
Figure 10: Realistic case: elevator δ
e
, total thrust X
T
, vec-
toring angle δ
v
and rudder δ
r
.
even though the airship is submitted to a wind dis-
turbance. This achievement is due to the fact that the
wind was included in the system model used to obtain
the actuators request.
Finally we can observe in figure 11 that the rolling
angle φ oscillates around zero, and the variation of the
airship yaw ψ following the reference-path heading.
Time [s]
φ [deg]
Time [s]
ψ [deg]
0 50 100
150
0
50 100 150
0
100
200
-20
-10
0
10
Figure 11: Realistic case: roll φ and yaw ψ angles (refer-
ence - dashed, output - solid).
As expected for low airspeeds, the control surfaces
authority is reduced, which leads to a slower correc-
tion of the lateral errors in these situations.
A GAIN-SCHEDULING APPROACH FOR AIRSHIP PATH-TRACKING
87

6 CONCLUSION
In this paper a gain scheduled optimal controller is
designed to solve the path-tracking problem of an air-
ship, valid over the entire flight envelope. The control
law is obtained from a coupled linear model of the
airship that allows to control the longitudinal and lat-
eral motions simultaneously. Due to the importance
of taking into account wind effects, which are rather
important due to the airship large volume, the wind
is included in the kinematics, and the dynamics is ex-
pressed as function of the air velocity.
The examples presented with the inclusion of wind
disturbances, demonstrate the effectiveness of this
single controller tracking a reference path over the en-
tire flight envelope. The implied variation of airspeed
represents a significant problem in an airship control
due to its influence to the system dynamics, as well as
to the actuators authority.
REFERENCES
˚
Astr
¨
om, K. J. and Wittenmark, B. (1989). Adaptive Control,
chapter 9: Gain Scheduling, pages 343–371. Addison-
Wesley Publishing Company, 1
st
edition.
Azinheira, J. R., de Paiva, E. C., and Bueno, S. S. (2002).
Influence of wind speed on airship dynamics. Jour-
nal of Guidance, Control, and Dynamics, 25(6):1116–
1124.
de Paiva, E. C., Azinheira, J. R., Ramos, J. J. G., Moutinho,
A., and Bueno, S. S. (2006). Project AURORA air-
ship: Robotic infrastructure and flight control experi-
ments. Journal of Field Robotics.
Elfes, A., Bueno, S. S., Bergerman, M., de Paiva, E. C.,
JR., J. G. R., and Azinheira, J. R. (2003). Robotic
airships for exploration of planetary bodies with an
atmosphere: Autonomy challenges. Autonomous Ro-
bots, (14):147–164.
Elfes, A., Bueno, S. S., Bergerman, M., and Ramos, J. J. G.
(1998). A semi-autonomous robotic airshipfor envi-
ronmental monitoring missions. In Proceedings of the
IEEE International Conference on Robotics and Au-
tomation, volume 4, pages 3449–3455, Leuven, Bel-
gium. IEEE Press.
Hygounenc, E. and Sou
`
eres, P. (2003). Lateral path-
following GPS-based control of a small-size un-
manned blimp. In Proceedings of the IEEE Interna-
tional Conference on Robotics and Automation, vol-
ume 1, pages 540–545, Taipei, Taiwan. IEEE Press.
Khalil, H. K. (2000a). Nonlinear Systems, chapter 12: Feed-
back Control, pages 485–498. Prentice-Hall, Inc., 3
rd
edition.
Khalil, H. K. (2000b). Nonlinear Systems. Prentice-Hall,
Inc., 3
rd
edition.
Merino, L., Caballero, F., de Dios, J. R. M., and Ollero, A.
(2005). Cooperative fire detection using unmanned
aerial vehicles. In Proceedings of the IEEE In-
ternational Conference on Robotics & Automation,
Barcelona, Spain.
Rao, J., Gong, Z., Luo, J., and Xie, S. (2005). Unmanned
airships for emergency managment. In Proceedings of
the IEEE International Workshop on Safety, Security
and Rescue Robotics, pages 125–130, Kobe, Japan.
IEEE Press.
Rugh, W. J. and Shamma, J. S. (2000). Research on gain
scheduling - survey paper. Automatica, 36(10):1401–
1425.
Silveira, G. F., Azinheira, J. R., Rives, P., and Bueno, S. S.
(2003). Line following visual servoing for aerial ro-
bots combined with complementary sensors. In Pro-
ceedings of the IEEE 11
th
International Conference
on Advanced Robotics, pages 1160–1165, Coimbra,
Portugal. IEEE Press.
Stevens, B. L. and Lewis, F. L. (1992). Aircraft Control and
Simulation. John Wiley and Sons, Inc., USA.
Xia, G. and Corbett, D. R. (2005). Cooperative control sys-
tems of searching targets using unmanned blimps. In
Proceedings of the 5
th
Worth Congress on Intelligent
Control and Automation, volume 2, pages 1179–1183,
Hangzhou, P.R.China. IEEE Press.
ICINCO 2006 - ROBOTICS AND AUTOMATION
88
