ONLINE HIERACHICAL CONTROL FOR LEGGED SYSTEMS

BASED ON THE INTERACTION FORCES

José R. Puga

Department of Electrical Engineering, Polytechnic Institute of Porto, 4200-072 Porto, Portugal

Filipe M. Silva

Department of Electronics, Telecommunications and Informatics, IEETA, University of Aveiro, 3810-193 Aveiro, Portugal

Boaventura R. da Cunha

Department of Electrical Engineering, University of Trás-os-Montes e Alto Douro, 5000-911 Vila Real, Portugal

Keywords: Legged robots, Biped locomotion, Online planning, Interaction forces.

Abstract: This paper presents a motion planning and control method with application in the field of legged robots. The

general aim is to explore a set of simple underlying principles that govern balance of posture and gait of

biped robots, and to develop control methodologies for such a highly unstable and non linear plants. The

proposed controller reflects a hierarchical structure based on the interaction forces between the foot and

ground and simple feedback rules used online. The algorithms are applied to a simulated 3-D leg model

with five degrees of freedom (DOF). The simulation analyses demonstrate the capability of the control

system to keep balance when the leg executes different tasks. To validate the proposed method several

aspects are investigated, such as the posture robustness on the level ground when subject to external

perturbations, the adaptation when standing in a moving platform and the improvements introduced by the

compensation of the tangential reaction forces.

1 INTRODUCTION

Biped locomotion, the core technology for a

humanoid robot, has attracted an enormous interest

around the world, both from the industry and the

academic communities. The major problems

associated with human-like walking results from the

high centre of gravity (COG) with a small contact

area to the ground. With other words, balance

maintenance is a central concern in order to engage

useful tasks, from standing upright posture to motion

goals. In what concerns control, the difficulty lies in

the uncertainty of the environment and the

limitations of the contact between the robot and the

environment. On the one hand, the advantages of

biped locomotion are well-known for irregular

terrains described by deterministic, but a priori

unknown models. On the other hand, the degree of

freedom formed between the foot and the ground is

unilateral and under-actuated, affecting the postural

stability (Goswami, 2004). The most prominent

stability measure to enhance trajectory-tracking

controllers and to analyse their stability is the

so-called zero moment point (ZMP) criterion

(Vukobratovic, 1990).

Current works in motion generation fall largely

into two categories: trajectory replaying and online

generation. The former is mainly characterised by

pre-planned trajectories that are then played back

during walking and modified online through

feedback (Hirai, 1998; Yamaguchi, 1999; Park,

2000). By contrast, the later generates a trajectory

online, feeding back the present state of the system

in accordance with the pre-provided goal of the

motion (Sugihara, 2002; Kajita, 2003). Planning and

control are executed in a unified way, although

requiring a larger amount of computation power.

Bearing these facts in mind, this paper aims to

explore a set of simple underlying principles that

261

Puga J., Silva F. and Cunha B. (2006).

ONLINE HIERACHICAL CONTROL FOR LEGGED SYSTEMS BASED ON THE INTERACTION FORCES.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 261-268

DOI: 10.5220/0001221702610268

 SciTePress

govern balance and to develop online control

methods for such a highly unstable and non-linear

plant. The approach followed in this paper consists

of studying a simple model but keeping enough

complexity to allow a clearly evaluation of the

control method. The algorithms are then applied to a

simulated 3-D robot model with a total of 5-DOF.

The main features of the proposed scheme are the

consideration of the interaction forces as the primary

control variable and the minimal dependency on

pre-programmed references.

The tasks to be performed include a variety of

motion goals specified in the intuitive Cartesian

space (e.g., hip coordinates, Centre of Gravity COG),

as well as in the joint space. The discussion includes

the choice of control principles, the selection and

grouping of control variables and measurements. The

scope of the paper covers the sagittal and lateral

planes for a robot model that stands itself on a

platform. The analysis will be carried out in a

dynamic simulation environment.

This paper is organised as follows. Section 2

describes the robot model, the sensorial requirements

and the tasks’ description. Section 3 presents the

online motion-control algorithm on which the

walking tasks are formulated. Section 4 discusses the

computer simulations used to illustrate the different

characteristics of the control algorithm. Section 5

concludes the paper and outlines the perspectives

towards future research.

2 SYSTEM AND TASK

DESCRIPTION

The control algorithms presented in this paper are

applied to a simulated 3-D robot model with 5-DOF

and 4-links (foot, shank, thigh and trunk). The Open

Dynamics Engine simulation library (Russell, 2004),

based on the Newtonian mechanics for articulated

rigid bodies, is used along with an interactive

graphical user interface. Figure 1 illustrates the

articulated system with a total weight of 5 kg and a

maximum height of 66 cm. The detailed parameters

of this model are summarised in Table 1.

Table 1: Robot and environment parameters.

Dimensions (m) Spring-damper model

Link

Mass

(kg)

(N/m) B

(Ns/m)

Trunk 4,00 0.06 0.15 0.330 50.0×10

1000.0

Thigh 0,70 0.04 0.04 0.165 Friction model

Shank 0,23 0.03 0.03 0.142

Foot 0,07 0.12 0.08 0.023

1.20 2.50

Figure 1: Three-dimensional 4-link model.

2.1 Actuators and Sensors

The leg proportions and the structure were selected

as a result of the desired similarity with the human

body. In order to provide adequate mobility the

model considers five rotary joints: two joints at the

ankle whose axes are orthogonal (pitch ν, roll ψ),

one at the knee (pitch ν) and two at the hip (pitch ν,

roll ψ). The contact of the foot with the constraint

surface is modelled through linear spring-damper

systems in the horizontal and vertical directions.

The specification of the actuators was obtained,

given the desired goals, by adjusting the values of

the maximum power, maximum torque and electrical

time-constant. These actuation constraints are

considered to evaluate the system’s ability when

performing a desired task. At the same time, a

walking robot can not afford to move on without

sensor feedback for even a smallest time segment.

While in motion or just standing still the robot must

continuously check the balance of the body. To this

purpose, it is considered feedback control from

several sensors, including angular position in each

joint, a three-axis inclinometer attached to the trunk

section and four force sensors inserted in the foot

corners. The sensors in the foot corners provide

information about the ground reaction forces and the

location of the centre of pressure (COP), as well as

about the full contact of the foot with the ground.

The inclinometer, the angular position in the joints

and the detention of full contact between the foot and

the ground provides the system with the ability to

detect the ground slope.

2.2 Task Description

A complete classification of possible tasks to be

performed is not feasible in view of the large variety

of cases that may occur, nor would such a

ICINCO 2006 - ROBOTICS AND AUTOMATION

262

classification be really useful to find a general

strategy of control. On the other hand, systems

capable of general legged locomotion are often

redundantly actuated. The immediate question is

how to exploit and coordinate the multiple degrees of

freedom. In general, it is observed that the joints

nearest to the ground (ankle and knee) are closely

related to the mobility and stability of the system,

and the more distant from the ground (hip) has a

compensation mechanism purpose.

The tasks to be performed include a variety of

motion goals specified in the intuitive Cartesian

space, both for the hip coordinates and the COG. A

generic robot task requires the execution of specific

motions prescribed in the joint space, as well. In the

present study, we will exploit mainly voluntary

movements such as the trunk inclination, either

sideways or front-backward. Accordingly, the task

description (refer to Figure 2) is provided with a first

block ensuring the fundamental motion directives

and a second block concerning individual joint

motions. However, it must be pointed out that all

five actuators will contribute to attain the motion

directives specified in the Cartesian space.

In this paper, it is assumed that the goal of the

articulated system (support-leg and trunk) is to

achieve a stable behaviour for a variety of motion

goals specified for the hip section, the centre of

gravity and other points, while it adapts to discrete

disturbances. More concretely, the desired task to be

performed consists of movements of crouch from

standing and then thrusts the body upwards to

assume an upright position again. Moreover, the

robot foot is assumed to be on two different support

surfaces: level ground and inclined ground. The main

goals are to investigate the posture robustness on the

level ground when subject to external perturbations,

the system’s adaptation when standing in a moving

platform and the improvements introduced by the

compensation of tangential forces.

A useful means to assess balance skill and gain

insight into postural control is by applying external

perturbations and recording reactions. One typical

disturbance experienced by a service robot is a

change in body mass. To demonstrate the capability

of adaptation to changes in mass, the system is

submitted to both loading and unloading of an

external load. There are other perturbations due to

external forces applied while the system is moving.

3 CONTROLLER BASED ON THE

INTERACTION FORCES

3.1 Highlight of the Method

Biped robots exhibit complex dynamic phenomena

that make difficult their analysis and control. A

major problem is the difficult relation between

planning and stability, namely the robot cannot

follow arbitrary motion commands. This difficulty

has justified a different line of thought where the

skill of locomotion emerges from the physical

interaction between the machine and the

environment itself (Fujimoto, 1998; Park, 2001).

In this line of thought, one approach based on the

interaction forces between the foot and the ground is

investigated. We emphasize the main role of these

forces as the key element through which new control

strategies are proposed to provide the required level

of compliance, adaptation and dynamic stability. The

proposed controller reflects a hierarchical structure

using force as the primary control variable and

simple feedback rules (Figure 2).

A block diagram of the resulting controller is

sketched in Figure 2, revealing the parallel operation

of a force control loop and a position control loop.

Hence, the control signal to the actuators is

composed of a force control action and a motion

control action integrated in a hierarchical way, as

follows:

fpp

ττ

(1)

where K

and K

are positive activation constants

(unitary sum) that define the dominance in the

contribution to the output. This parallel composition

of control actions aims at exploit the redundancy of

the system: a given actuator can be utilized to meet

more than one task requirement (thus providing

redundancy resolution).

A relevant feature of the proposed method is the

possibility of performing both indirect and direct

force control. The former is obtained via motion

control and without explicit closure of a force

feedback loop (solid line). The later, instead, offer

the possibility of controlling the contact force to a

desired value, thanks to the closure of a force

feedback loop (dashed line).

The position controller uses a time-dependent

algorithm that involves the tracking of pre-computed

trajectories using a PID control law. The following

subsection is aimed at presenting the implementation

ONLINE HIERACHICAL CONTROL FOR LEGGED SYSTEMS BASED ON THE INTERACTION FORCES

263

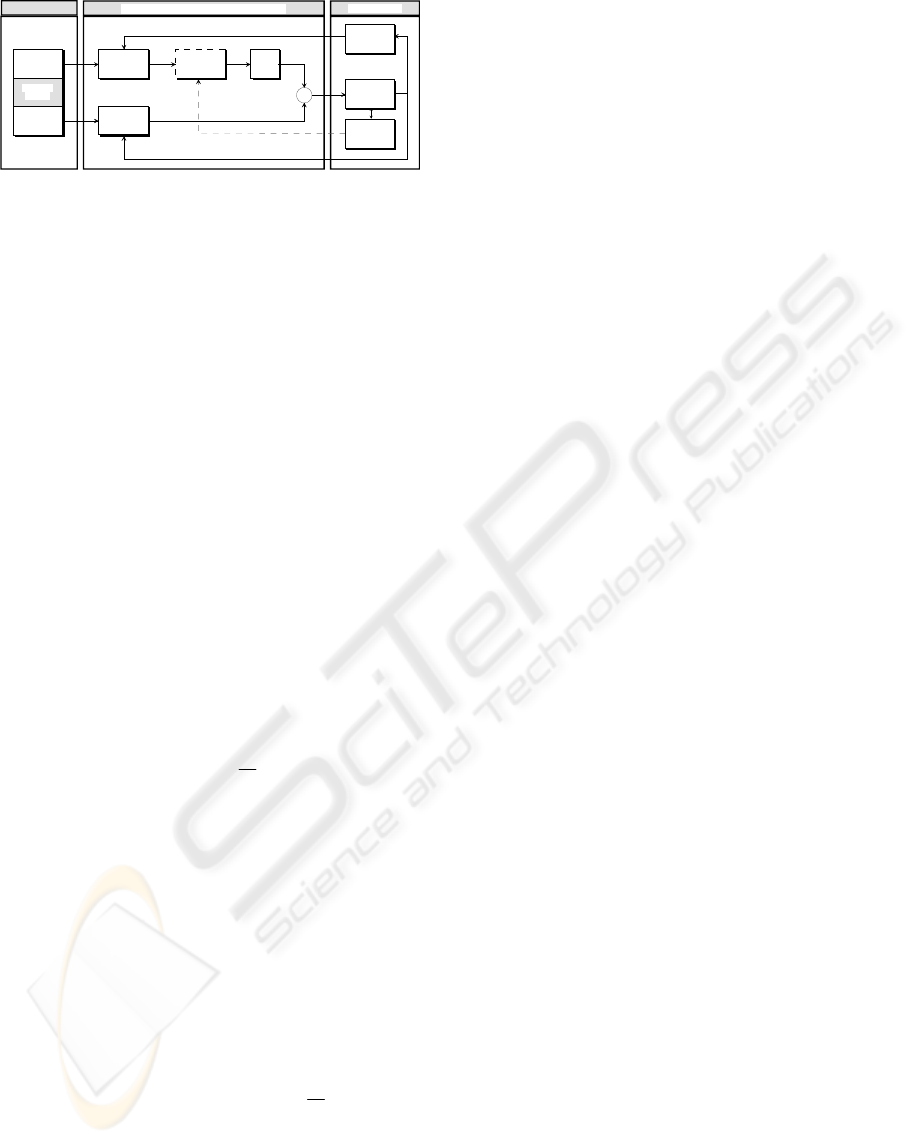
Task Description

OFF-LINE

Hierachical Position/Force Control System

Cartesian

Space

Joint

Space

MOTION

GOALS

ON-LINE

Force Virtual

References

Position

Controller

Robotic System

Direct

Kinematics

Robot

Model

Force Sensor/

Environment

Force

Controller

Figure 2: Blocks diagram of the hierarchical control

scheme.

of the force interaction control with reference to their

properties.

3.2 Force Interaction Control

As far as the force control is concerned, the tasks to

be performed depend on motion goals defined in the

Cartesian space. On the other hand, the variables to

be controlled are the reaction forces distributed along

the foot’s corners. In order to ensure the proper

behaviour through the execution of an interaction

task, the reference variables must be generated

online in result of the demands imposed to the

system. These are the variables that some force

control law must follow.

For the present purposes, the reference forces are

calculated through suitable actions on the position

errors in both horizontal and vertical directions. The

resultant normal reaction force is calculated from the

errors measured in the vertical coordinate (z-axis)

using a linear control law:

KezdtKezKf

ref

++=

∫

(2)

Here,

is the vertical position error given by

)( zz

ref

−

where

ref

and z are the desired and real

vertical coordinates,

ref

is the reference normal

force, and

and

are the proportional, the

integral and the derivative appropriated constant

feedback gains, respectively.

On the other hand, the desired location of the

centre of pressure (COP) is calculated from the

errors measured in the horizontal coordinates (x and

y axis), as follows:

KexdtKexKCOP

COP

ref

++=

∫

(3)

where

ref

COP

is the reference centre of pressure, ex

is the horizontal position error of the COP given by

)( xx

ref

− , where

ref

and

are the desired and

real horizontal coordinates,

COP

and

COP

are

the proportional, integral and derivative feedback

gains, respectively. All the feedback gains in

equations 2 and 3 were tuned with a standard

method. Finally, the reference COP is actively used

to calculate the distribution of the total reaction force

along the extremities of the support foot.

Having defined the reference forces, there are

many different ways to implement the compliance

control. This paper contributes with one strategy that

considers only the indirect force control. In spite of

the enhanced disturbance rejection provided by an

inner force control loop, a compliant behaviour can

be successfully achieved with the proposed solution.

In this line of thought, the signal forces obtained

for each corner of the foot are directly transformed

into joint torques by using the transpose of the

Jacobian matrix:

∑

(4)

Here,

is the Jacobian matrix which transforms

the differential variation in the joint space into the

differential variation of the end-effector’s frame i

(each foot corner) with respect to the reference frame

(located at the hip). The subscript

denotes the

transpose of a matrix. In the above treatment, it has

been implicitly assumed that the friction is large

enough to avoid any foot’s slippage. Nevertheless,

the general form of f

used in (4) may contain a

tangential force term. Further, the equation requires

lower computation than inverse kinematics or

dynamics equations and it is well-behaved since, for

a given force vector, a corresponding torque vector

can always be obtained even if the robot is in a

singular configuration.

In other words, the support leg “feels” the forces,

while the controller distributes them as driving

torques in order to regulate the desired high-level

directives. This strategy was generalised to all

degrees of freedom, from the ankle until the hip

joints. It is worth noting that, after some analytical

simplifications, a computationally simpler control

law can be derived as function of the desired normal

forces, tangential forces and COP. For example, the

output torque for the ankle joints can be written as:

() ()

cos sin

ref

ref ref

azhx

ref

ref d ref

azhYaza

xf lf

yf lf f

υψ

θθ

=− ⋅ − ⋅

⎡⎤

=+ −⋅

⎣⎦

(5)

where

ref

and

ref

are the reference COP,

ref

and

ref

are the reference interaction forces,

and

are the pitch and roll ankle angles respectively,

ICINCO 2006 - ROBOTICS AND AUTOMATION

264

(a) Movement sequences with the hierarchical integration.

(b) Hip’s vertical position under disturbances (left) and hip’s horizontal position (right): along the x-axis (in red) and along the y-axis (in blue).

(c) Location of the COP (solid line) and projected COG (dotted line) along the x-axis (in red) and along y-axis (in blue). Normalized normal

reaction forces at the corners of the foot: back right (in yellow), back left (in blue), front right (in green) and front left (in red).

(d) Temporal evolution of the torques at the ankle joints (left) and knee joint (left).

Figure 3: Simulation results for the robot standing on level ground when subject to external perturbations.

and l

is the foot’s height. This expression can be

useful whenever is necessary to sacrifice mobility

goals to ensure postural stability.

3.3 Hip Control

The trunk section has a particular role both in the

mobility and the stability of the overall system. On

the one hand, it has a great influence on the location

of the COG, what can be helpful to achieve a given

task. On the other hand, the postural stability

imposes limitations to the trunk motion: its

inclination must remain within a limited range of the

angular space and, when operating in steady state, it

must converge to a limit cycle. The idea of the

parallel control is to conciliate two imperatives –

ONLINE HIERACHICAL CONTROL FOR LEGGED SYSTEMS BASED ON THE INTERACTION FORCES

265

mobility and stability – that in many circumstances

are contradictories.

In this regard, the control structure of the trunk

section integrates also the control actions designed

on the basis of the position controller, as described

before. It is the sum of both components that actuate

over the hip joints, while providing some sort of

redundancy resolution. For certain motion tasks, it

can be necessary to adopt the same strategy with any

other joint.

4 SIMULATION RESULTS

In order to verify the effectiveness of the proposed

controllers several simulations are carried out.

Motivated by applications in biped locomotion, this

section focuses on the posture robustness of the

simplified model on the level ground when subject to

external perturbations, on the system’s adaptation

when standing in a moving platform and on the

improvements introduced by slip compensation.

4.1 Robustness to Perturbations

The first analysis illustrates the properties of the

proposed control scheme when the system is on the

level ground subjected to unpredictable

perturbations.

The results displayed below are based on the

following path: the system is standing, moves down

and up again to the initial posture in 5 seconds. The

initial state is set to

0.29

hip

zm=

and the desired

()

should be zero along the motion. The motion

planning is accomplished by prescribing the desired

trajectories using sinusoidal-based functions. The

controller’s performance is evaluated by applying

two unpredicted perturbations. The first perturbation

corresponds to a horizontal force of

(

)

(

)

=+ −,10,5

applied to the hip section at a pre-

defined instant of time (1.25 s) and sustained for

20 ms. At the same time, an external virtual load of

10% of the body mass is added instantaneously on

the hip at a pre-defined instant of time (3.25 s) and

removed when standing (6.25 s). The simulation

results are shown in Figure 3. It is observed that the

actual hip height profile was well-achieved, and the

system makes the necessary postural adjustments.

The system is only displaced by a few millimetres

and it has stabilised shortly after the push. The

results also demonstrate that mass adaptation is

feasible, for both loading and unloading of an

external load. The control method is able to

minimise the sway by generating a shear force

quickly at the ground to counteract the perturbation.

It depends on the latency at which it starts to resist

the push and the rate at which this force can be

increased. The last graphs show the temporal

evolution of the computed joint torques. Given the

proposed task, it is required a knee torque value that

is significantly greater than the others, while the

lateral joints require almost no torque.

4.2 Adaptation to Inclined Ground

The second analysis illustrates the emergence of an

appropriate behaviour when the system stands on an

inclined ground. The task performed is the same as

before, while the control system relies on the

inclinometer data to estimate slope changes. The

complete information data is depicted in Figure 4

(the top graph illustrates the movement sequence).

The task performed comprises forty cycles for

the robot’s motion (period of 3 s) and sixty cycles for

the platform’s motion (period of 2 s). The robot is

placed at a distance of 30 cm from the platform’s

rotational axis. Further, sinusoidal movements are

specified to the hip joints both in the sagittal and

lateral planes. For the roll axis, the amplitude is

0.15 rad and the period 3.5 s. For the pitch axis, the

amplitude is 0.1 rad and the period 5 s. The phase

planes represented in Figure 4-(e) show the limited

amplitude of the trajectories in each joint.

In summary, the proposed control scheme

demonstrates self-adaptation and robustness against

external forces and load changes. The automatic

adaptation of the proposed controller to inclined

grounds represents another relevant property.

4.3 Tangential Forces Compensation

In the third analysis, we study the influence of the

tangential forces and how they are regulated in the

proposed control scheme. Therefore, contact force

measurements are fully exploited hereafter to design

the indirect force control.

The objective is to thrust the body upwards to

assume an upright position, while regulating the

tangential reaction forces (zero tangential force) for a

short period of time (160 ms). The simulation results

are shown in Figure 5. The graphs show the

improvements induced on the tangential component

that, whereas the normal component remains

unchanged. In view of the previous results, the

introduction of these control variables could help to

avoid the foot’s slippage.

ICINCO 2006 - ROBOTICS AND AUTOMATION

266

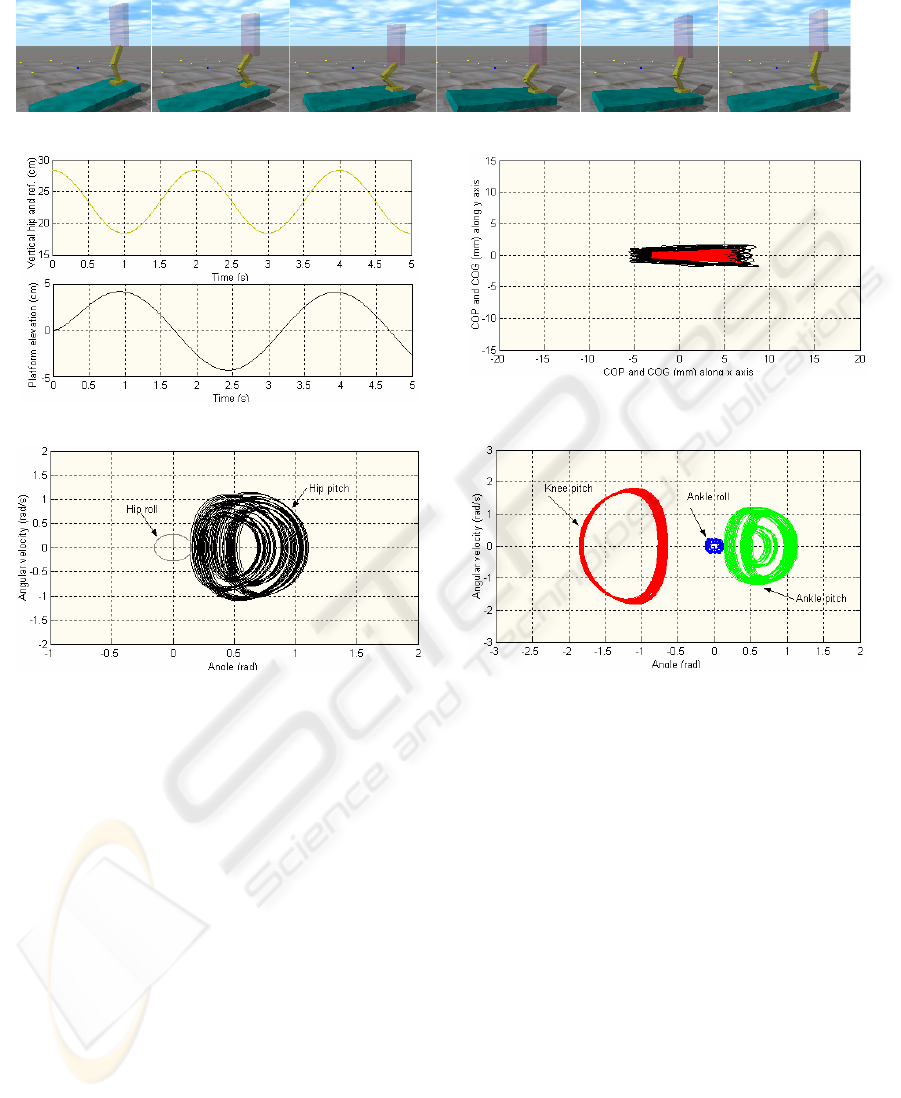
(a) Movement sequence during two seconds (the complete motion rounds 120 seconds).

(b) Hip and platform (point of support) positions for a complete cycle.

(d) Limit cycles observed in the hip joints.

(e) Limit cycles observed in the knee and ankle joints.

Figure 4: Simulation results obtained for the robot standing on inclined ground with variable slope.

5 CONCLUSIONS

This paper investigated motion-control algorithms

with application in the field of biped locomotion.

Topics such as the algorithm robustness and postural

stability were discussed through several experiments.

From the results achieved a few remarks ought to be

made. First, the Force Interaction Control is effective

to generate the desired leg motion, while assuring the

desired postural balance. The combination of

position and force control algorithms is essential to

exploit the system’s redundancy. Second, the results

illustrate the capability of the system to adapt to

external forces and to changes in the body mass.

Third, the results obtained provide an intuitive

understanding of the postural adaptation when the

system stands on an inclined ground with variable

slope.

Ongoing research focuses in two main directions:

i) to extend this study to a biped locomotion system;

ii) to apply the proposed schemes to different

walking tasks. Therefore, issues like active postural

recovery, inner force control loop, advanced

algorithms such as adaptive and learning strategies

are currently being challenged.

ONLINE HIERACHICAL CONTROL FOR LEGGED SYSTEMS BASED ON THE INTERACTION FORCES

267

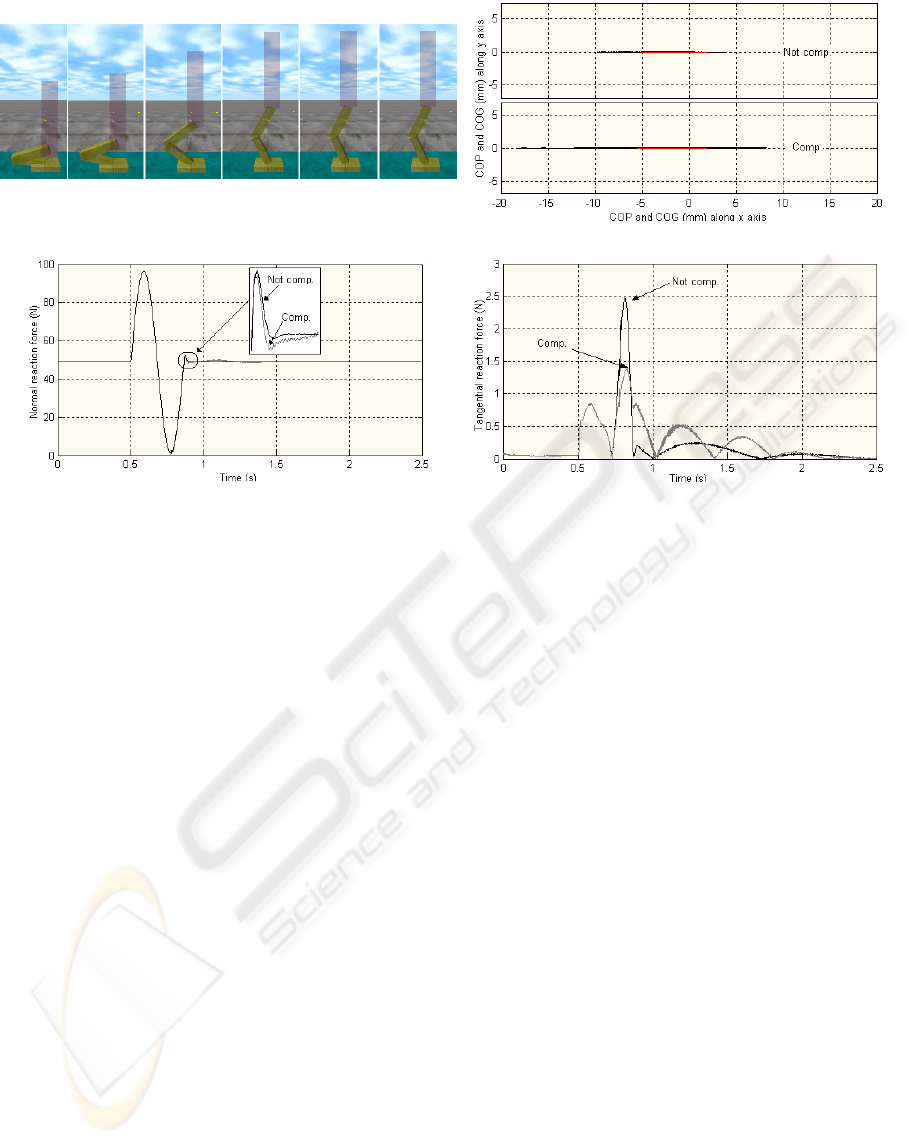
(a) Movement sequence for a fast (400 ms) thrusting the body upwards

to assume an upright position.

(b) Trajectory of COP (in black) and COG (in red).

(d) Time evolution of the tangential reaction forces.

Figure 5: Simulation results obtained for the robot standing on level ground with the regulation of the tangential forces.

ACKNOWLEDGEMENTS

The first author would like tacknowledgege FCT,

FEDER, POCTI, POSI, POCI, POSC and ISEP for

their support to R&D Projects and GECAD Unit.

REFERENCES

Goswami, A., V. Kallem, 2004. Rate of Change of

Angular Momentum and Balance Maintenance of

Biped robots. In the Proc. IEEE Int. Conf. on

Intelligent Robots and Systems, pp 3785-3790.

Vukobratovic, M., et al., 1990. The book, Biped

Locomotion – Dynamics, Stability, Control and

Application, Springer-Verlag.

Hirai, K., et al., 1998. The Development of Honda

Humanoid Robot. In the Proc. IEEE Int. Conf. on

R&A, pp. 1321-1326.

Yamaguchi, J-I., et al., 1999. Development of a Bipedal

Humanoid Robot – Control Method of Whole Body

Cooperative Dynamic Biped Walking. In the Proc.

IEEE Int. Conf. Robotics & Automation, pp. 368-374.

Park, J.H., H.C. Cho, 2000. An On-line Trajectory

Modifier for the Base Link of Biped Robots to

Enhance Locomotion Stability. In the Proc. IEEE Int.

Conf. Robotics & Automation, pp. 3353-3358.

Sugihara, T., Y. Nakamura, H. Inoue, 2002. Realtime

Humanoid Motion Generation Through ZMP

Manipulation Based on Inverted Pendulum Control. In

the Proc. IEEE Int. Conf. Robotics & Automation, pp.

1404-1409.

Kajita, S., et al., 2003. Resolved Momentum Control:

Humanoid Motion Planning Based on the Linear

Angular Momentum. In the Proc. IEEE Int. Conf.

Intelligent Robots and Systems, pp. 1644-1650.

Russell, S., 2004. Open Dynamics Engine v0.5, 29 May,

2004. http://www.ode.org.

Fujimoto, Y., A. Kawamura, 1998. Robust Biped Walking

with Active Interaction Control between Foot and

Ground. In the Proc. IEEE Int. Conf. on R&A, pp.

2030-2035.

Park, J., 2001. Impedance Control for Biped Robot

Locomotion. IEEE Trans. on Robotics & Automation,

vol. 17, n. 6, pp. 870-882.

ICINCO 2006 - ROBOTICS AND AUTOMATION

268