
THE HIERARCHICAL MAP FORMING MODEL
Luis Eduardo Rodriguez Soto
National Taiwan University
Taipei, Taiwan
Cheng-Yuan Liou
National Taiwan University
Taipei, Taiwan
Keywords:
Self-Organizing Maps, Q-learning, Hierarchical Control.
Abstract:
In the present paper we propose a motor control model inspired by organizational priciples of the cerebral
cortex. Specifically the model is based on cortical maps and functional hierarchy in sensory and motor areas
of the brain. Self-Organizing Maps (SOM) have proven to be useful in modeling cortical topological maps
(Palakal et al., 1995). A hierarchical SOM provides a natural way to extract hierarchical information from the
environment, which we propose may in turn be used to select actions hierarchically. We use a neighborhood
update version of the Q-learning algorithm, so the final model maps a continuous input space to a continuous
action space in a hierarchical, topology preserving manner. The model is called the Hierarchical Map Forming
model (HMF) due to the way in which it forms maps in both the input and output spaces in a hierarchical
manner.
1 INTRODUCTION
1.1 Cerebellar Organization
Modular organization is the norm in the cerebral cor-
tex, which is divided into specific dedicated areas. For
example, there are areas dedicated to visual process-
ing, auditory signal processing and somato-sensory
processing (Muakkassa and Strick, 1979; Palakal et
al., 1995). These specific dedicated areas within the
cortex are referred to as cortical maps. Another or-
ganizational principle in the cerebral cortex is hier-
archical processing, most vastly studied in the visual
regions. Areas dedicated to motor commands have
also been shown to be organized in a hierarchical
manner. This organization in the brain is not genet-
ically pre-defined and may come about through self-
organizing principles. Our work is also inspired by
the work of (Wolpert and Kawato, 1998) and their
modular selection and identification for control (MO-
SAIC) model The MOSAIC model is based on mul-
tiple pairs of forward (predictor) and inverse (con-
troller) models. Their architecture learns both the in-
verse models necessary for control as well as how to
select the set of inverse models appropriate for a spe-
cific environment. Learning in the architecture, origi-
nally driven by the gradient-descent method, has been
later implemented by other learning methods such as
expectation-maximization (EM) algorithm, and other
reinforcement learning methods. Their model is mo-
tivated by human psychophysical data, from which
it is known that an action selection process must be
driven by two different processes: a feedforward se-
lection based on sensory signals, and selection based
on the feedback of the outcome of a movement. The
basic idea behind the MOSAIC model, is that the
brain contains multiple pairs of forward (predictor)
and inverse (controller) models wich are tightly cou-
pled during both learning and use. We studied the
MOSAIC model and wanted to produce a a similar
model but one which acquires the relation between
predictors and controllers through self-organisation
principles, in order to reflect the existence of the brain
maps found in the cortex. Our model combines two
different learning techniques to imitate the organized
structure of the brain, with the purpose of producing
a biologically plausible control algorithm. The cur-
rent work is a work a progress, and the results pre-
sented here are from preliminary tests, and involved
the learning of actions, mapping from an input space
to an output space. Further testing will measure the
robustness of the system described in motor control
tasks.
167
Eduardo Rodriguez Soto L. and Liou C. (2006).
THE HIERARCHICAL MAP FORMING MODEL.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 167-172
DOI: 10.5220/0001221801670172
Copyright
c
SciTePress
Layer 2
Layer 1
Layer 3
Wc
Wc
Wc
1
2
3
Layer 0
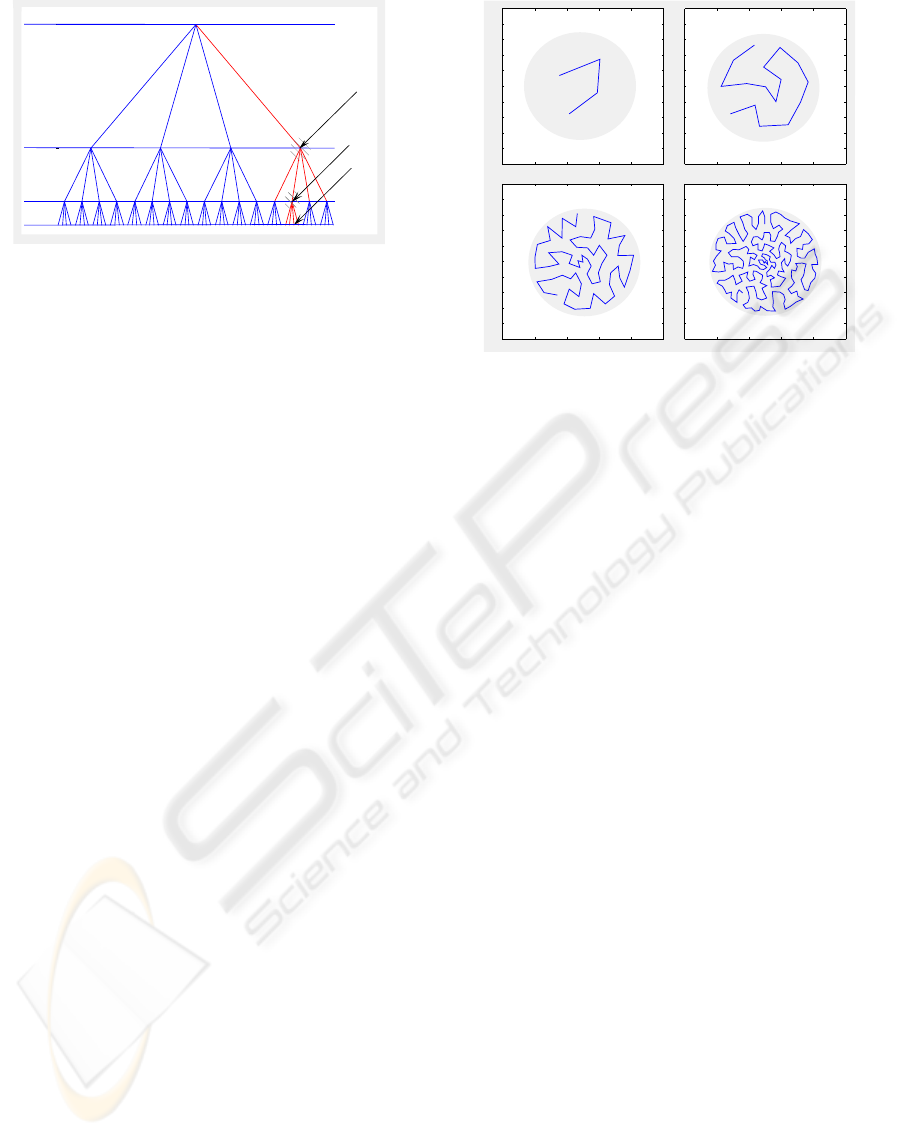
Figure 1: TSSOM with 4 layers and bf = 4.
1.2 Tree-Structured Self-Organizing
Maps
The Self-Organizing Map (SOM) was first introduced
by Teuvo Kohonen in 1981. A hierarchical SOM
called the Tree-Structured SOM (TS-SOM) was intro-
duced by Koikkalainen and Oja (1990), and extended
in Oja and Kaski (1999). Given that there is a vast
amount of publications regarding the SOM (Kohonen,
1998, 2001; Oja and Kaski, 1999) we do not present
the mathematical detail for it in this paper. Instead we
present the dynamics of the TS-SOM which we use
as part of our model.
1.2.1 Detail of TS-SOM
The TS-SOM (Oja et al., 1999) is composed of sev-
eral layers, where each layer of the tree is a standard
SOM (Kohonen, 2001). Every node not in the final
layer has bf child neurons in the layer below, where
bf is the branching factor. Layers are labeled in in-
creasing order, begining with a root layer or layer 0
as shown in Figure 1. Each layer l also represents
an SOM denoted M
l
and a neuron i in this layer can
be denoted by M
l
(i). Each layer l will then contain
n
l
= (bf)
l
neurons.
The child neuron j of neuron i in layer l will be de-
noted in the following manner: C
i
l
(j) where j ∈
{1, .., bf}; neuron j can only belong to layer l + 1,
therefore C
i
l
(j) = M
l+1
(j).
Training the TS-SOM TS-SOM is trained in a
layer by layer manner with the first layer trained no
differently than a standard SOM. In the remaining
layers only a subset of neurons are selected to com-
pete for a given input. When an input vector U (t) is
received at time t, neurons in the first layer all com-
pete, and a winner M
i
(∗) is selected. The winner se-
lects its neighbors defined by a time varying neighbor-
hood function, N (t).Only the child neurons of these
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Layer 1 Layer 2
Layer 3 Layer 4
Figure 2: TS-SOM with a branching factorof 4 and 4 layers.
selected neurons are allowed to compete for the input
in the next layer. This dynamic of selecting only the
children of the winning neuron and its
neighbors for competition reduces the search space
greatly (Oja et al, 1999). The neighborhood function
is also used during the updating phase, or the coop-
erative phase, in which the neighbors of the winning
neurons are allowed to update their weights towards
the current input.
Pseudo-code algorithm The dynamics of the TS-
SOM may be more clearly understod by following the
steps of the pseudo-code algorithm:
TS-SOM
Initialize
for CurrentLayer = 1 to L
while(not converged)
for i = 1 to CurrentLayer - 1
compete(C
∗
i−1
, U(t))
M
i
(∗) = winner(C
∗
i−1
)
update(M
i
(∗), N(t))
end
end while
end for
The update and compete subroutines behave as de-
fined for the standard SOM (Kohonen, 2001; ). We
define a small number ǫ as our convergence criterion
which is calculated recursively in the following man-
ner:
ǫ
t
= κǫ
t−1
+ ||w
c
t
− w
c
t−1
||
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
168

Q-table Contour Map Actuator 1
State TS-SOM
Actuator 1 Action
10 20 30 40 50 60
10
20
30
40
50
60
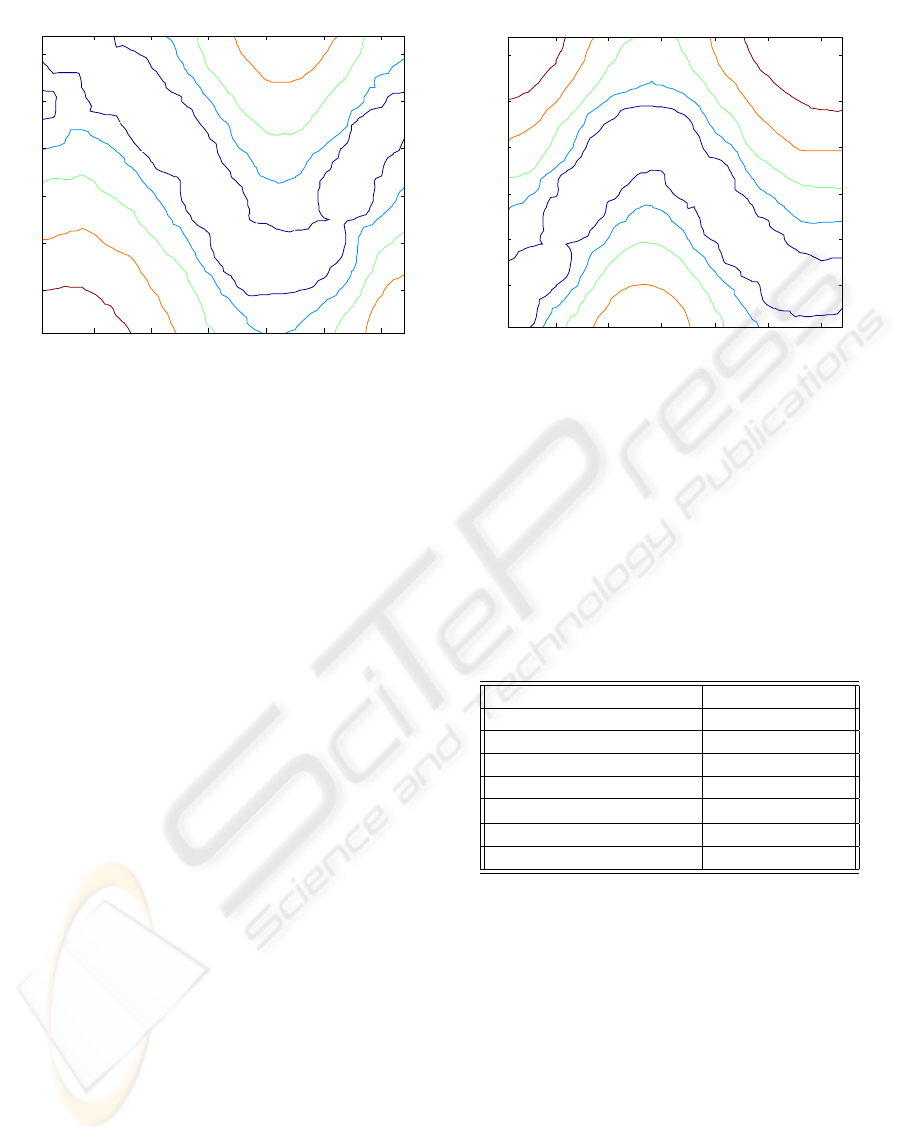
Figure 3: Q-value contour for actuator 1.
The term ||w
c
t
− w
c
t−1
|| represents the absolute value
of variation in the winning neuron’s weights after the
last update, and κdenotes a discount factor. We use
κ = 0.25 in the simulations presented in this paper.
Once ǫ is very small, for example ǫ ≤ 0.0025 we stop
the training.
In Figure 2 we see a trained 4 layer TS-SOM with bf
= 4. The TS-SOM is trained with a circular homo-
geneous density surface depicted by the shaded circle
in Figure 2. With each increasing layer, the TS-SOM
spreads more evenly over the input area, thus better
approximating the input space. In control applications
this property is very desirable, since we may abstract
higher dimensional input spaces to a 1 dimensional
space.
Thus the TS-SOM is utilized in the HMF model
to abstract higher dimensional spaces to hierarchical,
lower dimensional ones. The winning neurons of the
TS-SOM will conform the state vector, characterizing
the current state of the environment.
2 THE HMF MODEL
The HMF model applies Q-learning (Sutton and
Barto; 1998, Haykin, 1999; Watkins and Dayan,
1992) in order to map input vectors to actions. Af-
ter the TS-SOM has converged, it observes the en-
vironment as depicted in Figure 3. Each full it-
eration of the converged TS-SOM selects one win-
ning neuron per layer, forming a state vector
~
X =
[M
1
(∗), M
2
(∗), ..., M
L
(∗)]. This state information is
fed into a group of Q-tables, where each group con-
Q-table Contour Map Actuator 2
State TS-SOM
Actuator 2 Action
10 20 30 40 50 60
10
20
30
40
50
60
Figure 4: Q-value contour for actuator 2.
Figure 5: HMF model diagram. Combines TSSOM and Q-
learning.
trols one actuator (Figure 5). The Q-tables then select,
independenty, the highest valued actions in a hierar-
chical manner as each table receives more detailed
information about the current state, or select a ran-
dom action with a probability given by ε(t) which
decreases with time. The selected actions are added,
and fed to the actuators as in Figure 5. If there are L
layers in the TS-SOM we will have L corresponding
Q-tables per actuator. Each higher indexed table will
produce higher defined actions. The range of actions
per table is left to the designer to decide.
Depending on the outcome of the action selected
by the Q-tables, the enviroment will react and give a
reward signal, which is fedback to all groups of Q-
tables. The use of Q-learning for the HMF model
was motivated by the possibility that motor learning
in humans may be driven by a form of reinforcement
THE HIERARCHICAL MAP FORMING MODEL
169
TS-SOM State
Actuator 1 Action
Q-values Contour Map Actuator 1
10 20 30 40 50 60
10
20
30
40
50
60
-0.1
-0.2
-0.3
-0.4
-0.5
-0.1
-0.2
-0.3
-0.4
Figure 6: NQ-value contour for actuator 1.
signal (Holroyd and Coles, 2002). As in standard Q-
learning the selection of an accurate reward signal is
essential to assure the system will properly learn the
task at hand.
2.1 Neighborhood Q-learning
In the present model we use a version of Neighbor-
hood Q-learning, where the update rule for the Q-
tables is given by:
Q(s
t
, a
t
) ← Q(s
t
, a
t
) + α ∗ η (t) ∗ [r
t
+ 1 +
γ max
a
Q(s
t+1
, a) − Q(s
t
, a
t
)]
Where the parameter α is the learning rate, and r
t
is the reward received at the current time t; γ is
the discount factor. The term η(t) denotes the Q-
neighborhood, and it is a time decreasing function.
Similar neighborhood Q-learning functions have been
proposed in Smith (2001), and in Millan et al. (2002).
This forms the core of the HMF model, amodel which
is currently still under development. To show the ad-
vantages of using the HMF model for action control
tasks we setup a simulated environment. We use a
mechanism as that shown in Figure 8, where the base
does not move, it is only allowed to move 2 joints.
The task is to follow a dot in a circular motion, as pre-
sented in Smith (2001). In Figure 8 we also show the
last layer of our converged TS-SOM, which closely
fits the circular motion, in a topology preserving man-
ner. On each step a reward will be given equal to the
negative of the distance from the present input, plus
the radius of the sensor (r= 0.05). Thus, if the input
TS-SOM State
Actuator 2 Action
Q-Values Contour Map Actuator 2
10 20 30 40 50 60
10
20
30
40
50
60
-0.2
-0.1
-0.3
-0.4
-0.5
-0.5
-0.4
-0.4
-0.3
-0.2
-0.1
Figure 7: NQ-value contour for actuator 2.
data is inside the sensor a positive reward is given. We
divide the training of the HMF model in two periods,
one to learn to appropriate values for the TS-SOM,
and the second period to learn to match the input to
appropriate actions. We train our HMF model with
the parameters shown in Table 1.
Table 1: Parameters used during training.
TS-SOM size 6 layers, bf =2
Learning Rate 0.25
Initial Q-Neighborhood 20
Q-table Size 64 x 64
Training Steps 50000
Annealing Schedule e
−t/2000
Angle Range Actuator 1 0 - 1.6 radians
Angle Range Actuator 2 1.5 - 3.5 radians
The training is done over 50000 steps, following the
example set by Smith (2001), and the training is re-
peated 20 times. In Figure 9 we can see the per-
formance curve of our model contrasted to neighbor-
hood, and standard Q-learning averaged over the 20
simulations. After 20000 steps the average reward
has been maximized. Using neighborhood Q-learning
our HMF model receives higher rewards than stan-
dard Q-learning after convergence has been achieved,
but not higher than a single table neighborhood Q-
learning. While the hierarchical selection of actions
does not provide higher rewards, it does fare better
than standard Q-learning. Also, the use of hierarchi-
cal selection of actions explores the state space in a
more orderly fashion, in contrast to just selecting ran-
dom actions over a long period of time. This ordered
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
170
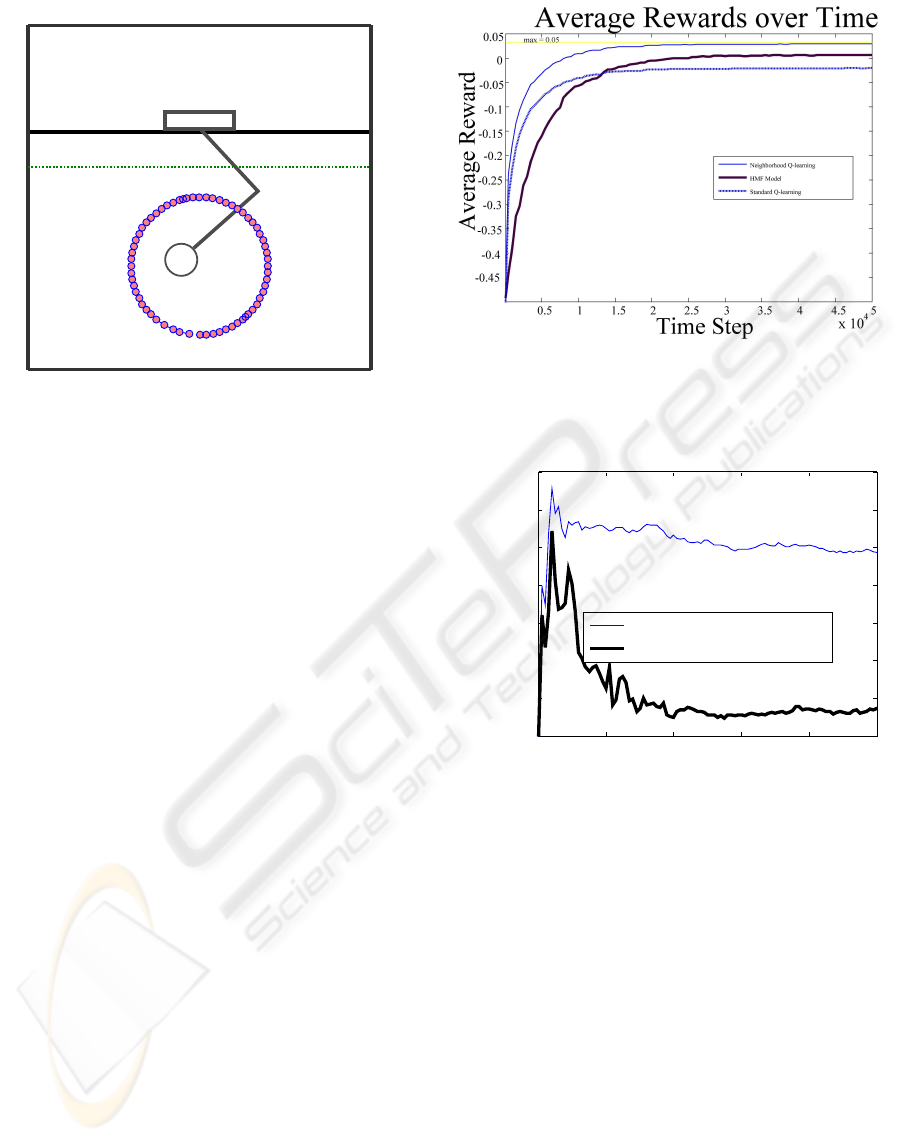
Figure 8: Simple 2 DOF mechanism used for action learn-
ing. The last converged layer of the TS-SOM is also shown.
exploration of the state space makes our model more
suitable for real world action learning tasks. In Figure
10. we compare the standard deviation, σ, of both Q-
learning update rules. The neighborhood Q-learning
minimizes the σ over time, thus beign more suitable
for stable control tasks, while in standard Q-learning
σ remains large throughout.
The Neighborhood Q-learning update rule also pre-
serves the topology in the action space. Since the
state vector
~
X, is received from the layers of the TS-
SOM, the states are topological neighbors in the in-
put space and in index number. Thus we expect that
actions should also be topologically similar in the Q-
table. That is the actions selected for neighbors in the
input space should be close to each other in the out-
put space. The use of the neighborhood Q-learning
ensures this as rewards are shared among neighbors
in the Q-table, thus actions close to each other in the
Q-table have similar values.
Figures 6 and 7 we see a contour mapping of a
single neighborhood Q-table. We may contrast these
contour plots to Figures 3 and 4 which are the contour
plots for Q-tables trained with the standard Q-learning
update rule. As we can see neghborhood Q-learning
maitains a topological relatioship across the table. In
Figures 3 and 4 we see that the actions values are not
similar between adjacent states, thus the mechanism
will only move in jerky motions. The training with
the neighborhood update rule produces smoothly out-
lined contours even during the early stages of training
due to the large initial neighborhood. In future imple-
mentations, currently under development and testing,
we will extend the model to allow a mapping to a con-
tinuous action range by using a softmax function as
that used in Millan et al. (2002).
Figure 9: Rewards received averaged over 20 simulations.
0 1 2 3 4 5
x 10
4
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
Time Step
Standard Deviation
Standard Deviation over Time
Standard Q-learning
Neighborhood Q-learning
Figure 10: Comparison of the Standard Deviation.
3 CONCLUSIONS
The HMF model presented here is a work in progress.
In the initial experiments it has shown to be very ef-
ficient at learning the intrinsic hierarchy of the task at
hand. Extracting the state information in a hierarchi-
cal manner allows the controller portion of the model
to react hierarchically. The use of the Neighborhood
Q-learning update rule greatly enhances learning, al-
lowing the model to learn a smooth mapping to the
state information. The use of the neighborhood up-
date rule also reduces the variance of the rewards re-
ceived over time, allowing for a more stable learning
curve, this is a desirable property for real life applica-
tions, since we can be more certain how the learning
system will behave under controlled conditions. The
THE HIERARCHICAL MAP FORMING MODEL
171

mapping in the output space is done in a topology pre-
serving fashion which produces smooth movements,
even at the earlier stages of learning, which allows for
quicker learning. Work is still needed to measure the
robustness of the learning system when trained under
the effect of disturbances. Future work envisions the
extension of this model from a discrete model to a
continuous one.
REFERENCES
Holroyd, C.B. Coles, M. (2002). The Neural Basis of
Human Error Processing: Reinforcement Learning,
Dopamine, and the Error-Related Negativity Psycho-
logical Review. Vol. 109, No. 4, 679–709.
Kohonen, T. (2001). Self-Organizing Maps. Springer Ver-
lag, Heidelberg, Germany.
Koikkalainen, P. and Oja, E. (1990). Self-organizing hierar-
chical feature maps. In Proceedings of International
Joint Conference on Neural Networks (IJCNN’90) In-
formation Systems.
Millan , J. Possenato, D. Dedieu, E. (2002). Continuous-
Action Q-Learning. Machine Learning. Springer,
Netherlands .
Muakkassa, K. F., Strick, P. L. (1979). Frontal Lobe Inputs
to Primate Motor Cortex. Evidence for Four Soma-
totopically Organized ”Premotor” Areas. Brain Re-
search. Elsevier/North-Holland Biomedical Press.
Oja, E. and Kaski ,S. (1979). Kohonen Maps. Elsevier
Science, Netherlands.
Palakal, M.J. Murthy, U. Chittajallu, S.K. Wong, D. (1995).
Tonotopic Representation of Auditory Responses Us-
ing Self-Organizing Maps. Mathematical and Com-
puter Modelling. Elsevier Science, Netherlands.
Smith, A.J. (2001). Applications of the self-organising map
to reinforcement learning. Neural Networks. Elsevier,
United States
Simon Haykin. (1999). Neural Networks. Prentice-Hall,
New Jersey, Second Edition.
Watkins,C. Dayan,C. (1992). Technical Note: Q-Learning.
Machine Learning. Springer, Netherlands.
Wolpert, D. Kawato, M. (1998). Multiple Paired Forward
and Inverse Models for Motor Control. Neural Net-
works. Elsevier, United States
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
172
