ICA for Surface Electromyogram

Ganesh R. Naik

, Dinesh K. Kumar

, Sridhar P. Arjunan

and M. Palaniswami

School of Electrical and Computer Engineering, RMIT University,

GPO Box 2476V. Melbourne, Victoria-3001, Australia.

Department of Electrical and Electronic Engineering, The University of Melbourne,

Parkville, Victoria-3010, Australia.

Abstract. Surface electromyogram (SEMG) is an indicator of the underlying

muscle activity and can be useful for human control interface. One difﬁculty in

the use of SEMG for identifying complex movements is the mixing of muscle

activity from other muscles, referred to cross-talk. Similarity in frequency and

time domain makes the separation of muscle activity from different muscles ex-

tremely difﬁcult. Independent Component Analysis (ICA) is a useful technique

for blind source separation. This paper reports investigations to test the effec-

tiveness of using ICA for such applications. It determines the impact of different

conditions on the reliability of the separation. The paper reports the evaluation

of issues related to the properties of the signals and number of sources. The pa-

per also tests Zibulevsky’s method of temporal plotting to identify number of

independent sources in SEMG recordings. The results demonstrate that ICA is

suitable for SEMG signals when the numbers of sources are not greater than the

number of recordings. The inability of the system to identify the correct order and

magnitude of the signals is also discussed. It is observed that even when muscle

contraction is minimal, and signal is ﬁltered using wavelets and band pass ﬁl-

ters, Zibulevsky’s sparse decomposition technique does not identify number of

independent sources.

1 Introduction

Blind Source Separation (BSS) by Independent Component analysis (ICA) is emerg-

ing as a new standard in signal processing and data analysis. ICA has received much

attention over the last years in the ﬁeld of neural computations and bio medical sig-

nal processing due to its potential applications to the array signal processing such as,

separation of Biosignals especially SEMG. Research that isolates MUAP originating

from different muscles and motor units has been reported in 2004 [1], where success

is reported in the isolation of the different MUAP with applications for decomposing

the SEMG at low levels of muscle activation. Recently a denoising method using ICA

and high pass ﬁlter is used to suppress the interference of ECG in SEMG recorded

from trunk muscles has been reported [2]. ICA has also been proposed for unsuper-

vised cross talk removal from SEMG recordings of the muscles of the hand [3]. From

literature, ICA appears to be the emerging technology with solutions to most of the

requirements for ﬁltering SEMG.

R. Naik G., K. Kumar D., P. Arjunan S. and Palaniswami M. (2006).

ICA for Surface Electromyogram.

In Proceedings of the 2nd International Workshop on Biosignal Processing and Classiﬁcation, pages 51-60

DOI: 10.5220/0001223200510060

 SciTePress

Surface electromyography (SEMG) is a kind of non invasive and dynamic mea-

surement of muscular function. It is a result of the superposition of a large number of

transients that have temporal and spatial separation that is semi-random. These tran-

sients are the motor unit action potentials (MUAP). SEMG from different muscles that

need to be separated often have spectral overlaps and this makes the use of spectral ﬁl-

tering not suitable for separating the signals effectively. Wavelets combine the temporal

and spectral properties and are suitable for separating some of the signals that may not

be separable using spectral ﬁltering, but are limited for continuous signals with spectral

overlaps. Further, the above techniques are suitable only when there is prior information

of the signals.

ICA is a multi dimensional signal processing technique to separate signals from

different sources into distinct components. ICA algorithms have been considered to be

information theory based unsupervised learning rules. Given a set of multidimensional

observations, which are assumed to be linear mixtures of unknown independent sources

through an unknown mixing source, an ICA algorithm performs a search of the de mix-

ing matrix by which observations can be linearly translated to form Independent output

components. It is a very convenient technique for source separation as it requires very

little information of the sources or the signals to be separated, and with the availability

of easy to use software packages, is becoming very popular for numerous applications.

ICA can be employed in unsupervised situations and this makes it very attractive for

number of applications. However, the success of using commonly used ICA algorithms

for signal separation is dependent on some properties of the signals and the recordings.

These include the linearity of the mixing medium, small sensor noise, and the inde-

pendence of the underlying sources as well as the equity of the number of sources and

the number of recordings or sensors. Further, most of the ICA techniques available are

based on the assumption that there is no propagation delay. When any one of these is

not met, the output of that separation technique is questionable. The other assumption

that determines the suitability of ICA is that the number of sources need to be less than

or equal to the number of recordings.

When SEMG is recorded, most of the times the number of recording channels cor-

respond to the active muscles being measured, with no spare recording to account for

the artefact. If the artefact was to be removed using ICA, the source of the artefacts

would be another independent source, and in such a situation, the number of sources

would exceed the number of recordings. To overcome the difﬁculty of separation of

signals when the number of sources exceeds the number of recordings, an alternate to

the entropy based ICA is the use of blind source separation using clustering. Zibul-

vesky et al. [4] showed that during the overcomplete case (number of sources exceeds

number of recordings) audio recordings can be separated by making the data sparse. It

is often the density of the SEMG that carries the information related to the activity of

the speciﬁc muscle and making it sparse may alter the information content of the sig-

nal. In applications where the muscle is weakly active and the signal strength is small,

this may provide a solution. This paper uses Zibulvesky’s sparse decomposition tech-

nique for SEMG to tests by making the data sparse whether it is possible to separate the

independent sources.

2 Surface Electromyogram

Surface electromyography (SEMG) is the recording of the electrical activity of skeletal

muscle from the skin surface. It is a non-invasive recording of the muscle activity and

ﬁnds application in sports training, rehabilitation, machine and computer control, occu-

pational health and safety, and for identifying posture disorders. There is a near linear

relationship between RMS of SEMG and the ﬁnger ﬂexion-extension - suggesting the

use of SEMG for bio-control for anthropomorphic tele-operators and Virtual Reality

entertainment [5]. There is useful information of the posture from the muscle activ-

ity of the lumbar muscles. SEMG amplitude and frequency have been investigated as

indicators of localized muscular fatigue. Amplitude and spectral information of EMG

have also been exploited to estimate force of muscle contraction and torque [6]. These

applications require automated analysis and classiﬁcation of SEMG.

SEMG may be affected by various factors such as the muscle anatomy (number of

active motor units, size of the motor units, the spatial distribution of motor units); mus-

cle physiology (trained or untrained, disorder, fatigue); nerve factors (disorder, neuro-

muscular junction); contraction (level of contraction, speed of contraction, isometric/non-

isometric, force generated); artefacts (crosstalk between muscle, ECG interference),

and recording apparatus factors (recording method, noise, electrode’s properties, record-

ing sites). The anatomical/ physiological processes such as properties and dimensions

of tissues, and force and duration of contraction of the muscle are known to inﬂuence

the signal. SEMG is also inﬂuenced by onset of muscle fatigue, and contraction of other

muscles in the close vicinity. Each of the factors can be used as a criterion to categorise

the input signal.

One property of the SEMG is that the signal originating from one muscle can gen-

erally be considered to be independent of other bioelectric signals such as electrocar-

diogram (ECG), electro-oculargram (EOG), and signals from neighbouring muscles.

This opens an opportunity of the use of independent component analysis (ICA) for this

application.

2.1 ICA for SEMG Applications

Signals from different sources can get mixed during recording. Often it is required to

separate the original signals, and there is little information available of the original sig-

nals. An example is the cocktail party problem. Even if there is no (limited) information

available of the original signals or the mixing matrix, it is possible to separate the origi-

nal signals using independent component analysis (ICA) under certain conditions. ICA

is an iterative technique that estimates the statistically independent source signals from

a given set of their linear combinations. The process involves determining the mixing

matrix. The independent sources could be audio signals such as speech, voice, music,

or signals such as bioelectric signals.

A number of researchers have reported the use of ICA for separating the desired

SEMG from the artefacts and from SEMG from other muscles. While details differ, the

basic technique is that different channels of SEMG recordings are the input of ICA al-

gorithm.The fundamental principle of ICA is to determine the un-mixing matrix and use

that to separate the mixture into the independent components. The independent compo-

nents are computed from the linear combination of the recorded data. The success of

ICA to separate the independent components from the mixture depends on the prop-

erties of the recordings. When examining the various attempted applications of ICA,

two properties of SEMG recordings appear important; (i) number of sources exceeding

number of recordings and (ii) statistical properties. These two properties of SEMG are

examined below.

Number of Sources Exceed Number of Recordings. When SEMG is recorded, most

of the times the number of recording channels correspond to the active muscles being

measured, with no spare recording to account for the artefact. If the artefact was to be

removed using ICA, the source of the artefacts would be another independent source,

and in such a situation, the number of sources would exceed the number of recordings.

It is thus important to determine the conditions under which standard ICA could be used

to remove artefacts from biosignal recordings when the number of sources may exceed

the number of recordings. To analyse this, consider the set of recordings to be a vector

x and the pure signals (unknown) to be a vector s. Then

x = As (1)

where A is an unknown mixing matrix. The output of ICA algorithm is an estimate of

un-mixing matrix W so that

s = Wx

= WAs

(2)

It is evident that WA = I, identity matrix. If the number of recorded data is less than

the number of true independent sources (A is not a square matrix), running standard

ICA on this kind of data will never give truly independent source. The estimated inde-

pendent components will be a mixture of those true independent sources with element

of W as the scale factor. To prove the same, consider two channel recordings x of three

independent sources s and express it as:

= a

+ a

(3)

= a

+ a

(4)

Consider the estimated un-mixing matrix,

W = [w

] (5)

generated using standard ICA algorithm on that data. The estimated independent com-

ponents can be written as:

= w

+ w

= w

+ a

)

+ w

+ a

)

(6)

= w

x1+ w

= w

+ a

)

+ w

+ a

)

(7)

If none of the coefﬁcient of mixing matrix A is zero means that all three sources are

present in both mixtures x

and x

As A is a full rank matrix, then there is no column

or row dependency. Under these conditions, there is no W that will be able to isolate

one source from others. The only possible way that the estimated output would look

very similar to one of the independent sources is when its corresponding magnitude is

higher than others. Since the number of actual independent sources of SEMG signal

recorded from electrode is unknown (and is believed to be many), standard ICA will

not be suitable for applications except when the magnitude of some of the sources is

comparatively much higher.

Statistical Properties of SEMG Recordings. Signals from Gaussian sources cannot be

separated from their mixtures using ICA [7], making such signals unsuitable for ICA

applications. Mathematical manipulation demonstrates that all matrices will transform

this kind of mixtures to another Gaussian data. However, a small deviation of density

function from Gaussian may make it suitable as it will provide some possible max-

imization points on the ICA optimization landscape, making Gaussianity based cost

function suitable for iteration. If one of the sources has density far from Gaussian, ICA

will easily detect this source because it will have a higher measure of non Gaussianity

and the maxima point on the optimization landscape will be higher. If more than one

of the independent sources has non Gaussian distribution, those with higher magnitude

will have the highest maxima point in the optimization landscape. Given a few signals

with distinctive density and signiﬁcant magnitude difference, the densities of their lin-

ear combinations will tend to follow the ones with higher amplitude. Since ICA uses

density estimation of a signal, the components with dominant density will be found

easier.

Signals such as SEMG have probability densities that are close to Gaussian while

artefacts such as ECG and motion artefacts have non Gaussian distributions. From the

above, it can be suggested that ICA may suitably isolate some of the above signals,

while its efﬁcacy for separating the others maybe questionable. It is difﬁcult to identify

the quality of separation of EMG from one muscle and the neighbouring muscles, or

that of EEG from one channel to the neighbouring recording sites, making it difﬁcult to

conﬁrm or negate the above.

3 Sparse ICA

Sparse representation of signals which is modeled by matrix factorisation has been re-

ceiving great deal of interest in recent years. The research community has researched

many linear transforms that make audio, video and image data sparse, such as the dis-

crete cosine transform (DCT), the Fourier transform, the wavelet transform and their

derivatives [8]. Chen et al. [9] discussed sparse representations of signals by using large

scale linear programming under given over complete basis (e.g., wavelets). Olshausen

et al. [10] represented sparse coding of images based on maximum posterior approach

but it was Zibulvesky et al. who noticed that in the case of sparse sources, their lin-

ear mixtures can be easily separated using very simple ”geometric” algorithms. Sparse

representations can be used in blind source separation. When the sources are sparse,

smaller coefﬁcients are more likely and thus for a given data point t. if one of the

sources is signiﬁcantly larger, the remaining ones are likely to be close to zero. Thus

the density of data in the mixture space, besides decreasing with the distance from the

origin shows a clear tendency to cluster along the directions of the basis vectors. Spar-

sity is good in ICA for two reasons. First the statistical accuracy with which the mixing

matrix A can be estimated is a function of how non-Gaussian the source distributions

are. Thus, roughly speaking the sparser the sources are the less data is needed to esti-

mate A. Secondly the quality of the source estimates given A, is also better for sparser

sources.

A signal is considered sparse when values of most of the samples of the signal do

not differ signiﬁcantly from zero. These are from sources that are minimally active.

Zibulevsky et al. have demonstrated that when the signals are sparse, and the sources

of these are independent, these may be separated even when the number of sources

exceeds the number of recordings [4]. The over-complete limitation suffered by nor-

mal ICA is no longer a limiting factor for signals that are very sparse. Zibulevsky also

demonstrated that when the signals are sparse, it is possible to determine the number of

independent sources in a mixture of unknown signal numbers. One application where

the use of blind source separation for SEMG is required is when the signal strength is

very small, and the sources are minimally active, such as during maintained posture.

This leads to the argument of the use of Zibulevsky’s ICA technique to separate muscle

activity originating from muscles that are minimally active. It also provides the basis

for identifying the number of active independent sources in the mixture to validate the

use of ICA for SEMG application.

3.1 Identiﬁcation of Sources using Plotting of Sparse Data

Zibulvesky et al. developed a simple probabilistic method for over determined ICA

source separation. For a more general case they used maximum aposteriori approach

which includes the situation of over complete dictionary and more sources than sen-

sors. They have also demonstrated the combination of clustering and shortest path de-

composition technique to be faster and more robust. This required the estimation of

the mixing matrix before hand by clustering and then reconstruction of the sources by

shortest path decomposition. They demonstrated the separation of up to six different

audio sounds mixed into two mixtures (recordings). During maintained posture of the

unloaded hand, muscles are minimally active and the SEMG signal strength is very

small. Hence SEMG is expected to be sparse in these conditions. The plotting of the

recording against each other would be expected to demonstrate the number of indepen-

dent sources. As the ﬁrst stage, it is necessary to suitably linearly transform and ﬁlter the

signals to ensure the signals are sufﬁciently sparse. There are number possible methods

that are available. Most common one is spectral ﬁltering of the data for the signal to be

sparse in the time domain. The ﬁlter properties such as frequency and order needs to be

selected according to the frequency content of the signal. Typically, while maintaining

the properties of the original signal, and desiring to make the signal sparse, ﬁltering is

performed where approximately 1

or 12% of the signal is removed and 85% to 90%

of the energy of the original data is kept. The signal may also be ﬁltered in time domain

by applying a threshold function to the signal data.

4 Methodology

4.1 Experiment

The experiment was conducted where Zibulevsky’s technique was applied to SEMG of

minimally active muscles to determine the number of distinct independent sources in

the mixture, thus establishing whether this test could be used for isolating muscle activ-

ity from different muscles.The experiments were approved by the Human Experiments

Ethics Committee of the University. A male subject participated in the experiment.

The experiment used 2 channel EMG conﬁgurations as per the recommended recording

guidelines. A two channel, continuous recording BIO PAC equipment was used for this

purpose. Raw signal sampled at 2000 samples/ second was recorded. The target sites

were shaved to remove hairs and cleaned with alcohol wet swabs. Ag/AgCl electrodes

(AMBU Blue sensors from MEDICOTEST, Denmark) were mounted on appropriate

locations close to the selected muscles in the right forearm. The SEMG was recorded

from muscles of the right arm while performing simple ﬁnger posture (gesture), where

the muscles were minimally activated at approximately 5% maximum voluntary con-

traction (MVC). The aim of the experiment was to determine the effectiveness of using

Zibulevsky’s technique where the signals (SEMG recordings) in time domain are plot-

ted against each other to identify number of independent sources in the mixture that is

the muscle activity.

4.2 Analysis

The aim of this experiment was to justify the underlying theory of the use of ICA

for separation of the EMG signals. This will determine if it is appropriate to assume

that the sources of MUAPs can be considered as independent. For this purpose, the

SEMG recordings were ﬁrst made sparse. The recorded signals were analysed using

MATLAB software. The aim was to make the data sparse. The Signals were initially

ﬁltered with Butterworth ﬁlter of order four so that the energy of the signal after ﬁltering

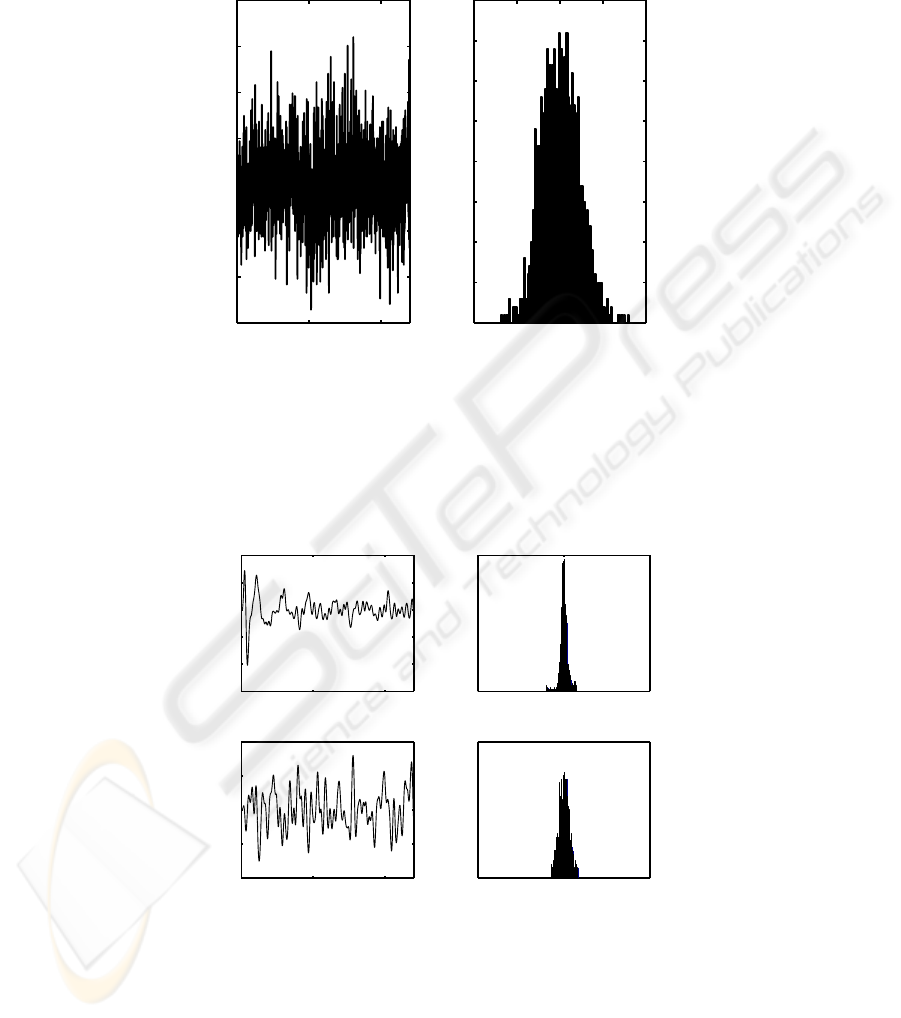
was maintained at 90%. Corresponding histograms were plotted and compared with the

original histograms to make sure that they maintain the gaussianity as shown in Figure

(1) and Figure (2). Scatter plotting was done by the resultant sparse signals. These were

visually observed to identify the number of sources.

5 Results and Observations

The SEMG data was made sparse by band pass ﬁlter. Figure (1) and Figure (2) shows

the histograms for both original and sparse data. Figure (3) shows the scatter plot of the

sparse recorded SEMG signals. From the scatter plot it can be visualised that there are

no distinguishable lines in the directions of the basis vectors, which shows that even

0 500 1000

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

0 0.01 0.02 0.03 0.04

Fig.1. Example of one Channel EMG Recording of ﬁnger movements and the Histograms.

0 500 1000

−0.015

−0.01

−0.005

0.005

0.01

−0.05 0 0.05

0 500 1000

−0.01

−0.005

0.005

0.01

−0.05 0 0.05

Fig.2. Two Channel Sparse EMG Recordings and the respective Histograms.

when SEMG is recorded from minimal contraction and ﬁltered, the data is not suitable

to determine the number of independent sources in SEMG recordings.

The sparseness of the SEMG recordings is observed from the histogram plot. While

the original data was modestly sparse, the signal was made more sparse after ﬁltering,

where nearly 12% of the energy was removed (based on 1 sigma). The results demon-

strate that sparse decomposition technique is not able of identifying the independent

sources in SEMG recordings. This could suggest that either the signal was not sparse

enough even after the ﬁltering, or the sources are not independent, or the number of

sources was very large.

−0.015 −0.01 −0.005 0 0.005 0.01

−8

−6

−4

−2

x 10

−3

Fig.3. Scatter plot of Sparse data using Zibulevsky’s Sparse Decomposition Technique.

6 Discussions and Conclusion

The results of the experiments demonstrate that using Zibulvesky’s sparse decompo-

sition technique, it is not possible to determine the number of independent sources in

SEMG recordings. The reason for this could be either because there are very large

numbers of independent sources, or that SEMG signal, even at extremely low levels of

contraction and after ﬁltering, is not sparse enough. From the above, it is concluded

that Zibulvesky’s Sparse Decomposition technique cannot be used for the separation of

SEMG signals.

References

1. Hideo, Nakamura., Masaki, Yoshida., Manabu, Kotani., Kenzo, Akazawa., Toshio, Mori-

tani. : The application of independent component analysis to the multi-channel surface elec-

tromyographic signals for separation of motor unit action potential trains, Vol. 14. Journal of

Electromyography and Kinesiology, (2004) 423 - 432

2. Yong, Hu., Li, X. H., Xie, X. B., Pang, L. Y., Yuzhen, Cao., Luk, K. D. K. : Applying Inde-

pendent Component Analysis on ECG Cancellation Technique for the Surface Recording of

Trunk Electromyography, IEEE Engineering in Medicine and Biology 27th Annual Confer-

ence, Shanghai (2005)

3. Greco, A., Costantino, D., Morabito, F. C., Versaci, M. A. : A Morlet wavelet classiﬁcation

technique for ICA ﬁltered SEMG experimental data, Vol. 1. Neural Networks Proceedings

of the International Joint Conference, (2003) 66 - 71

4. Zibulevsky, M., Pearlmutter, B. A., Boﬁll, P., Kisilev, P. : Blind source separation by sparse

decomposition in a signal dictionary, In: Roberts, S. J. and Everson, R. M.(eds): Independent

Components Analysis: Principles and Practice, Cambridge University Press (2000)

5. Gupta, V., Reddy, N. P. : Surface electromyogram for the control of anthropomorphic tele-

operator ﬁngers, Vol. 29. Student Health Technology Information, (1996) 482 - 487

6. Moritani, T., Muro, M. : Motor unit activity and EMG power spectrum during increasing

force contraction, Vol. 56. Eur. J. Appl. Physio. Occup. (1987) 260 - 265

7. Hyvarinen, A., Karhunen, J., Oja, E. :Independent Component Analysis, John Wiley, New

York (2001)

8. Mallat, S. :A wavelet tour of signal processing, Cambridge University Press (2000)

9. Chen, S., Donoho, D.L. :Atomic decomposition by basis pursuit,Vol. 20. C, SIAM J. Sci.

Comput. (1999) 33 - 61

10. Olshausen, B.A., Millman, K.J. :Learning sparse codes with a mixture-of-Gaussians

prior,vol. 12. Advances in neural information processing systems, MIT Press (2000) 841