Shape Factor’s Effect on a Dynamic Cleaners Swarm

⋆

Yaniv Altshuler

, Israel A. Wagner

1,2

and Alfred M. Bruckstein

Computer Science Department, Technion, Haifa 32000 Israel

IBM Haifa Labs, MATAM, Haifa 31905 Israel

Abstract. This work discusses an impossibility result for the Dynamic Coop-

erative Cleaners problem, and the relation of a speciﬁc geometric feature of the

problem, known as the shape factor, to the efﬁciency of the operating swarm. The

dynamic cooperative cleaners problem assumes a grid, having “contamination”

points or tiles that form a connected region of the grid. Several agents move in

this contaminated region, each having the ability to “clean” the place it is located

in. The ”contaminated” tiles expand deterministically, simulating a spreading of

contamination, or ﬁre. This problem, as well as a cooperative cleaning protocol

for it and its analysis, were ﬁrst introduced in [1]. The equivalence of this problem

to another interesting multi agents problem was demonstrated in [2] by utilizing

results relevant to the problem in order to design a cooperative hunting protocol

for a swarm of UAVs. The results of [1] contain a generic lower bound for the

cleaning time of any multi agents system which is designed to entirely clean an

expanding contaminated area. This work enhances this bound, while discussing

the effect of the region’s shape factor (i.e. the ratio between the region’s bound-

ary and its area) and the swarm’s cleaning efﬁciency. As a result, a tighter lower

bound is produced, establishing a new and more generic impossibility result for

the problem.

1 Introduction

In recent years signiﬁcant research efforts have been invested in design and simulation

of multi-agent robotics and intelligent swarms systems — see e.g. [3,4] or [5–7] for

biology inspired designs (behavior based control models, ﬂocking and dispersing mod-

els and predator-prey approaches, respectively), [8–11] for economics applications and

[12] for a physics inspired approach). Unfortunately, the mathematical geometrical the-

ory of such multi-agents systems is far from being satisfactory, as pointed out in [13]

and many other papers.

In this work we discuss the dynamic variant of the Cooperative Cleaners problem,

ﬁrst presented in [14], in which agents must work in a dynamic environment — where

changes may take place, that are independent and certainly not caused by the agents’

activity. The problem assumes a grid, part of which is ‘dirty’, where the ‘dirty’ part is a

connected region of the grid. On this dirty grid region several agents move, each having

⋆

This research supported in part by the Ministry of Science Infrastructural Grant No. 3-942 and

the Devorah fund.

Altshuler Y., A. Wagner I. and M. Bruckstein A. (2006).

Shape Factor’s Effect on a Dynamic Cleaners Swarm.

In Proceedings of the 2nd International Workshop on Multi-Agent Robotic Systems, pages 13-21

DOI: 10.5220/0001223300130021

 SciTePress

the ability to ‘clean’ the place (‘tile’, ‘pixel’ or ‘square’) it is located in (similar works

appear in [15–17]). The dynamic variant of the cooperative cleaners problem (presented

in [1] and described in section 2) involves a deterministic evolution of the environment,

simulating a spreading contamination (or spreading ﬁre). Once again, the goal of the

agents is to clean the spreading contamination in as little time as possible. In the spirit

of [18] simple robots with only a bounded amount of memory are considered (i.e. a

ﬁnite-state-machines).

A cooperative swarm cleaning protocol for the problem and a basic analysis of, as

well as various experimental results are presented in [1], whereas a comparison of this

swarm protocol to an A

∗

based omniscient centralized algorithm is discussed in [19]. A

scheme of a cooperative hunting protocol, designed to be used by a swarm of unmanned

air vehicles seeking evading targets, which is based on the cleaning protocol mentioned

above is described in [2]. This work discusses the effect of a certain geometric feature

of the dirty region (known as the shape factor) on the cleaning time of the agents (see

section 3).

2 The Dynamic Cooperative Cleaners Problem

We shall assume that the time is discrete. Let G be a two dimensional grid, whose

vertices have a binary property of ‘contamination’. Let cont

(v) state the contamination

state of the vertex v at time t, taking either the value “on” or “off”. Let F

be the dirty

sub-graph of G at time t, i.e. F

= {v ∈ G | cont

(v) = on}. We assume that F

is a

single connected component.

Let a group of k agents that can move across the grid G (moving from a vertex to

its neighbor in one time step) be placed at time t

on F

(we focus on the cleaning

problem, and not on the discovery problem).

Each agent is equipped with a sensor capable of telling the condition of the tile

it is currently located in, as well as the condition of the 8-neighbors of this tile. An

agent is also aware of other agents which are located in its current position, and all

the agents agree on a common direction. Each tile can contain any number of agents

simultaneously.

When an agent moves to a vertex v, it has the possibility of causing cont(v) to

become off. The agents do not have any prior knowledge of the shape or size of the

sub-graph F

except that it is a single and simply connected component.

Every d time steps the contamination spreads. That is, if t = nd for some positive

integer n, then :

∀v ∈ F

∀u ∈ 4 − neighbors(v) , cont

t+1

(u) = on

The agents’ goal is to clean G by eliminating the contamination entirely, meaning

that the agents must ensure that :

∃t

success

s.t F

success

= ∅

In addition, it is desired that this time span t

success

will be minimal.

3 Results

Since we know no easy way to foretell whether k agents can successfully clean an

instance of the Dynamic Cooperative Cleaners problem, producing bounds for the pro-

posed cleaning protocol is important for estimating its efﬁciency.

The completion of the cleaning mission at time t means that S

= 0. By showing

that at a speciﬁc time t, S

is always larger than zero, it is shown that the mission

could not be completed until that time, regardless of the nature of the cleaning protocol

utilized by the agents.

For producing this bound, the contaminated region was assumed to spread in such

a way that creates the minimal number of new contaminated tiles. Having no addi-

tional information, this can be guaranteed by assuming that whenever the contamina-

tion spreads, it is somehow organized as a digital sphere (as was the case in the bound

presented in [1]). This, however, is rarely the case, since in the course of the expansions

and erosion process of the contamination, the probability for the contaminated region

to be accidently maintained in the form of a digital sphere, is very low. As a result, we

are interested in examining a variant of this bound, in which the contaminated region is

not assumed to be kept in the shape of a digital sphere.

3.1 Deﬁnitions

Let S

denote the size of the contaminated region F at time t, namely the number of grid

tiles in F

. Let d denote the number of time steps between two contamination spreads.

The boundary of the contaminated region F is denoted as ∂F , deﬁned as :

∂F = {(x, y) | (x, y) ∈ F ∧ (x, y) has an 8 neighbor in (G \ F )}

Let ψ(F

) denote the shape factor of F

, deﬁned as the ratio between the perimeter

of F

and its area, namely :

ψ(F

) =

|∂F

3.2 Detailed Analysis

Note that a lower bound for the cleaning time is in fact an upper bound for the agents’

performance. Let us assume that the agents are working in 100% efﬁciency, meaning,

each time step every agent cleans a single tile. After (d − 1) time steps k agents will

thus clean k · (d − 1) tiles, and thus we know that S

d−1

≥ S

− (d − 1) · k

In the d-th time step, the agents clean another portion of k tiles, but the remaining

contaminated tiles spread their contamination to their 4-neighbors and cause new tiles

to become contaminated. We are interested in the minimal number of tiles which can

become contaminated at this stage.

As the assumption that F

is continuously preserved in the shape of a digital sphere

is too rigid, we are interested in constructing a method that will provide us with tighter

predictions. For achieving this, we assume that the shape factor of the contaminated

region is kept bounded by some value Ψ throughout the entire evolution of F

, namely :

∀t ψ(F

) ≥ Ψ (1)

Since every new contaminated tile is a 4-neighbors of some v ∈ F

, the total number

of new contaminated tiles is at least the number of boundary tiles of F

, namely |∂F

Since we are interested in the minimal number of new contaminated tiles, we can use

the deﬁnition of ψ(F

) and write :

t+d

≥ S

− d · k + ψ(F

) · S

(2)

Since ∀t ψ(F

) ≥ Ψ we can then write :

Lemma 1.

t+d

≥ (1 + Ψ ) · S

− d · k

As to the explicit value of S

for some t = i · d we can quickly see that :

Lemma 2.

= S

i·d

≥ (1 + Ψ )

· S

− d · k ·

i−1

j=0

(1 + Ψ)

For ﬁnding the time in which the agents may be able to complete the mission suc-

cessfully (meaning that S

≤ 0) we require that :

(1 + Ψ)

· S

− d · k ·

i−1

j=0

(1 + Ψ)

≤ 0 (3)

(note that this does not guarantee the completion of the mission, but rather contradicts

the impossibility of the completion of the mission, meaning that a successful completion

of the mission is enabled). This requirement can also be written as follows :

d · k

≤

i−1

j=0

(1 + Ψ)

i−1

j=0

(1 + Ψ)

j−i

(4)

Remembering that Ψ > 0, we then use the expression describing the sum of a

geometric progression and see that :

i−1

j=0

(1 + Ψ)

j−i

(1 + Ψ)

−i

((1 + Ψ)

− 1)

(1 + Ψ) − 1

1 − (1 + Ψ)

−i

(5)

Combining equations 4 and 5 the following is produced :

Theorem 1. For a contaminated region F

of size S

such that F

spreads every d time

steps, and such that ∀t ψ(F

) ≥ Ψ , the number of agents required for a successful

cleaning of F

within at most (i · d) time steps is at least :

k =

· Ψ

d · (1 − (1 + Ψ)

−i

)

Note that since ∀F

|∂F

| ≤ S

we can see that ∀F

ψ(F

) ≤ 1. On the other

hand, for any region F

the minimal value of ψ(F

) is obtained when F

is organized

in the shape of a digital sphere (let us denote this value by Ψ

SP HERE

, and note that

SP HERE

> 0). Hence, we are only interested in 0 < Ψ

SP HERE

≤ Ψ ≤ 1. Note that

for Ψ = Ψ

SP HERE

a lower bound similar to this of [1] can be derived from Theorem 1.

However, unlike the case of Ψ = Ψ

SP HERE

, using larger values for Ψ yields better

estimations for the minimal number of agents which are required for a successful com-

pletion of the mission. This means that if it can be shown for some contaminated region

that its shape factor is kept bounded by some Ψ throughout its cleaning process, then

a tighter prediction for the minimal k needed for this problem is available.

Let F

be a contaminated region of size S

such that F

spreads every d time steps

and such that ∀t ψ(F

) ≥ Ψ (we know that the number of agents required for a success-

ful cleaning of F

within at most t = (i · d) time steps is at least k

·Ψ

d·(1−(1+Ψ )

−i

)

Then, for following Corollaries are derived from Theorem 1 :

Corollary 1. For some contaminated region H

of size α · S

(for some α ≥ 0) such

that H

spreads every d time steps and such that ∀t ψ(H

) ≥ Ψ the number of agents

required for a successful cleaning of H

within at most t = (i · d) time steps is at least :

= α

· Ψ

d · (1 − (1 + Ψ)

−i

)

= α · k

Corollary 2. For some contaminated region H

of size S

such that H

spreads every

α · d time steps (for some α >

) and such that ∀t ψ(H

) ≥ Ψ the number of agents

required for a successful cleaning of H

within at most t = (i · d) time steps is at least :

= α

−1

· Ψ

d ·



1 − (1 + Ψ)

−



∼ α

−1

· k

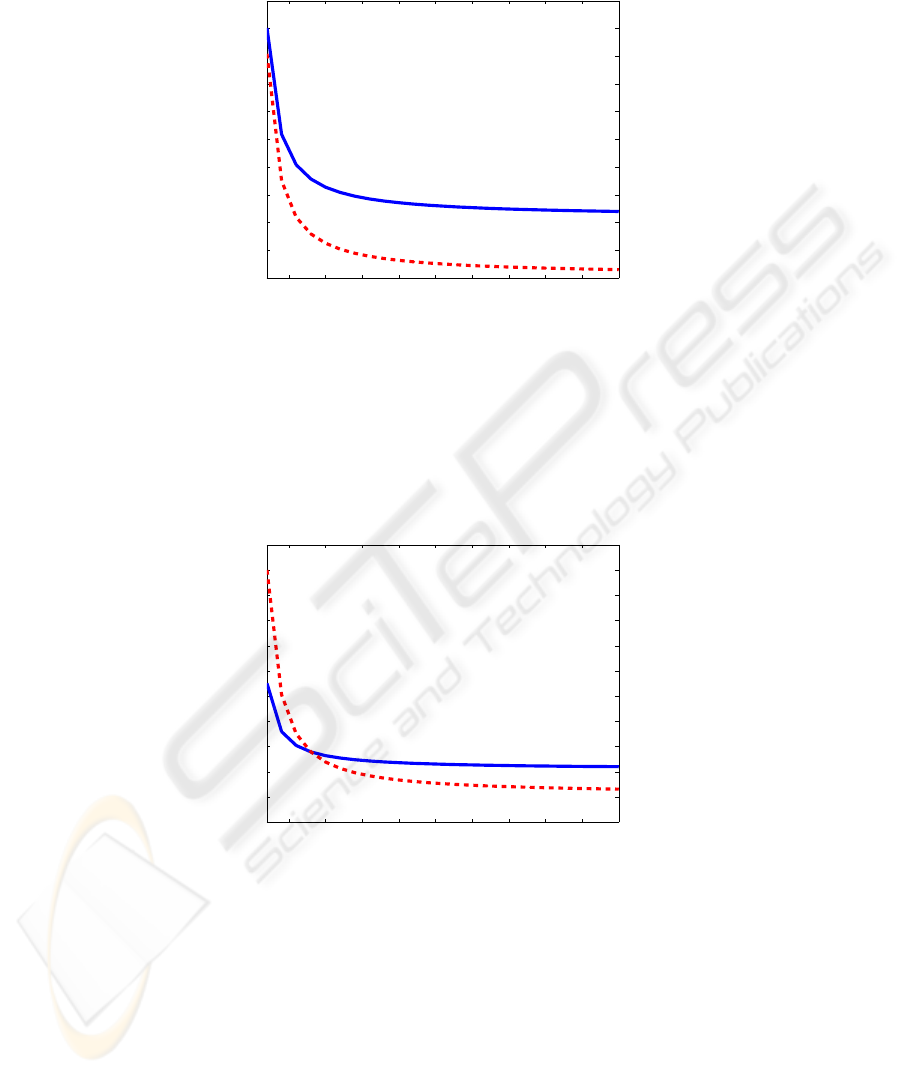
An example of Corollary 2 appears in Figure 1.

Note that if for some region F

it holds that d → ∞ (meaning that the contamina-

tion does not spread at all, for all practical reasons) then using De l’H

opital’s rule on

Corollary 2 we see that :

lim

α→∞

−1

· S

· Ψ

d ·



1 − (1 + Ψ)

−



· Ψ

d · i ln(1 + Ψ)

and since for every 0 < Ψ < 1,

ln(1+Ψ )

< 2 we see that k

≥

d·i

(which is also

intuitively correct).

Corollary 3. For some contaminated region H

of size S

such that H

spreads every

d time steps and such that ∀t ψ(H

) ≥ α · Ψ (for some 0 < α ≤

) the number of

agents required for a successful cleaning of H

within at most t = (i · d) time steps is

at least :

= α

1 − (1 + Ψ)

−i

1 − (1 + α · Ψ)

−i

· k

For large values of i,

1−(1+Ψ )

−i

1−(1+α·Ψ )

−i

= 1 and so k

= α · k

An example of Corollary 3 appears in Figure 2.

The previous Corollaries as well as Theorem 1 present various ways of predict-

ing a lower value which bounds the number of agents required for successfully solv-

ing an instance of the dynamic cooperative cleaners problem. In addition, once such

a lower bound was established, the effects of changes in the initial problem’s features

(e.g. spreading speed, shape factor, etc’) on this bound are discussed. Let us assume

that a certain cleaning protocol for the problem was constructed, which is able to direct

some of its cleaning resources to actively controlling the geometric features of the re-

gion to be cleaned. Meaning — instead of cleaning as much tiles as possible, cleaning

the shape so its boundary area is kept limited. It is obvious that since the shape factor

of the region is artiﬁcially controlled, we may expect an acceleration in the operation of

the agents using this protocol (due to Corollary 3). However, since some of the agents’

resources are diverted from the cleaning mission (since those agents are used for main-

taining the required shape factor), this improvement in the agents’ performance will be

compensated by the resources spent on the maintenance of the region’s shape factor.

This can be described as follows — let f(Ψ) ∈ (0, 1) denote the slowdown function of

the cleaning protocol caused by maintaining the shape factor bounded by Ψ . Thus, we

examine the following variation of Theorem 1 :

k =

· Ψ

d ·



1 − (1 + Ψ)

−i·f(Ψ)



In order to obtain the minimal number of agents needed for such a cleaning protocol,

we ﬁrst much ﬁnd the optimal value for the percentage of the cleaning efforts allocated

to maintaining the shape factor. Since we assume the cleaning protocol is able to select

the level of Ψ in which the region’s shape factor is maintain, Theorem 1 can be written

as follows :

Theorem 2. For a contaminated region F

of size S

such that F

spreads every d

time steps, and assuming that a cleaning protocol which is able to artiﬁcially preserve

the shape factor of F

is used (with a slowdown function f(Ψ )), the number of agents

required for a successful cleaning of F

within at most (i · d) time steps is at least :

k = min



· Ψ

d · (1 − (1 + Ψ)

−i·f(Ψ)

)



SP HERE

≤ Ψ ≤ 1



For example, imagine a protocol whose slowdown function is f(Ψ ) = Ψ. Namely,

the protocol suffers no slowdown when it is completely focused on cleaning F

, while

preserving the region to be organized as a digital sphere (i.e. the shape with the minimal

shape factor) the time it takes it to complete the cleaning is

S P HERE

·t the time required

without this slowdown. Using Theorem 2 we can see that :

k = min



· Ψ

d · (1 − (1 + Ψ)

−i·Ψ

)



SP HERE

≤ Ψ ≤ 1



A short discussing considering this example appears in Figure 3.

25 50 75 100 125 150 175 200 225 250

d (time steps between spreads)

Number of agents

S = 1000, Psi = 0.1

Cleaning within 500 time steps

Cleaning within 250 time steps

Fig.1. An example of Corollary 2. The two graphs represent the minimal number of agents as a

function of the spreading speed d. In addition, results of the change in the cleaning time permitted,

are presented. Notice that for most values of d (number of time steps between spreads) the ratio

between the two values of minimal numbers of agents requiredequals the ratio of the two cleaning

times, whereas for faster spreading regions (smaller values of d) the price for demanding faster

cleaning is much smaller.

25 50 75 100 125 150 175 200 225 250

d (time steps between spreads)

Number of agents

S = 1000

Cleaning within 500 time steps, Psi = 0.2

Cleaning within 250 time steps, Psi = 0.1

Fig.2. An example of Corollary 3. The two graphs represent the minimal number of agents as a

function of the spreading speed d. In addition, results of the change in the cleaning time allowed

and the shape factor of the contaminated region are presented. Notice that for different values

of d, sometimes a “simple” shape with less cleaning time produces a smaller requirement of

k while in other cases longer cleaning times for higher Ψ values are preferred. This example

demonstrates how various features of the problem (in this case — the spreading speed) may

signiﬁcantly inﬂuence designers of multi agents systems.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Psi

Agents

S = 1000, d = 50, i = 10, t = 500

Fig.3. An example of Theorem 2. For minimizing the number of agents required for a successful

completion of the mission, the optimal value of Ψ should be calculated. Once available, it allows

the cleaning protocol to optimally partially allocate its resources for maintaining the shape factor

of the region. Notice how in this example, using this optimal value results in a minimal require-

ment for 11 agents, while focusing solely on cleaning the region produces a demand for at least

20 agents (and diverting too much resources towards maintaining the shape factor in the lowest

value possible yields a lower bound of 40 agents).

References

1. Altshuler, Y., Bruckstein, A.M., Wagner, I.A.: “Swarm Robotics for a Dynamic Cleaning

Problem”, in “IEEE Swarm Intelligence Symposium 2005”, pp. 209–216, (2005).

2. Y.Altshuler, V. Yanovsky, I.A.Wagner, A.M. Bruckstein: “The Cooperative Hunters - Ef-

ﬁcient Cooperative Search For Smart Targets Using UAV Swarms”, Second International

Conference on Informatics in Control, Automation and Robotics (ICINCO), the First In-

ternational Workshop on Multi-Agent Robotic Systems (MARS), pp. 165–170, Barcelona,

Spain, (2005).

3. I.A. Wagner, A.M. Bruckstein: “From Ants to A(ge)nts: A Special Issue on Ant—Robotics”,

Annals of Mathematics and Artiﬁcial Intelligence, Special Issue on Ant Robotics, Kluer

Academic Publishers, vol. 31, Nos. 1–4, pp. 1–6, (2001)

4. L.Steels: “Cooperation Between Distributed Agents Through Self-Organization”, Decentral-

ized A.I - Proc. ﬁrst European Workshop on Modeling Autonomous Agents in Multi-Agents

world, Y.DeMazeau, J.P.Muller (Eds.), pp. 175–196, Elsevier, (1990)

5. R.C.Arkin: “Integrating Behavioral, Perceptual, and World Knowledge in Reactive Naviga-

tion”, Robotics and Autonomous Systems, 6:pp.105-122, (1990).

6. M.J.Mataric: “Designing Emergent Behaviors: From Local Interactions to Collective Intel-

ligence”, In J.Meyer, H.Roitblat, and S.Wilson, editors, Proceedings of the Second Interna-

tional Conference on Simulation of Adaptive Behavior, pp.432-441, Honolulu, Hawaii, MIT

Press, (1992).

7. T.Haynes, S.Sen: “Evolving Behavioral Strategies in Predators and Prey”, In Gerard Weiss

and Sandip Sen, editors, Adaptation and Learning in Multi-Agent Systems, pp.113-126.

Springer, (1986).

8. B.P.Gerkey, M.J.Mataric: “Sold! Market Methods for Multi-Robot Control”, IEEE Transac-

tions on Robotics and Automation, Special Issue on Multi-robot Systems, (2002).

9. G.Rabideau, T.Estlin, T.Chien, A.Barrett: “A Comparison of Coordinated Planning Methods

for Cooperating Rovers”, Proceedings of the American Institute of Aeronautics and Astro-

nautics (AIAA) Space Technology Conference, (1999).

10. S.M.Thayer, M.B.Dias, B.L.Digney, A.Stentz, B.Nabbe, M.Hebert: “Distributed Robotic

Mapping of Extreme Environments”, Proceedings of SPIE, Vol. 4195, Mobile Robots XV

and Telemanipulator and Telepresence Technologies VII, (2000).

11. M.P.Wellman, P.R.Wurman: “Market-Aware Agents for a Multiagent World”, Robotics and

Autonomous Systems, Vol. 24, pp.115–125, (1998).

12. D.Chevallier, S.Payandeh: “On Kinematic Geometry of Multi-Agent Manipulating System

Based on the Contact Force Information”, The 6

International Conference on Intelligent

Autonomous Systems (IAS-6), pp.188–195, (2000).

13. G.Beni, J.Wang: “Theoretical Problems for the Realization of Distributed Robotic Systems”,

Proc. of 1991 IEEE Internal Conference on Robotics and Automation, pp. 1914–1920, Sacra-

mento, CA, April (1991)

14. I.A. Wagner, A.M. Bruckstein: “Cooperative Cleaners: A Case of Distributed Ant-Robotics”,

“Communications, Computation, Control, and Signal Processing: A Tribute to Thomas

Kailath”, pp. 289–308, Kluwer Academic Publishers, The Netherlands, (1997)

15. Polycarpou, M., Yang, Y. and Passino, K.: “A Cooperative Search Framework for Distributed

Agents”, In Proceedings of the 2001 IEEE International Symposium on Intelligent Control

(Mexico City, Mexico, September 5–7). IEEE, New Jersey, pp. 1–6, (2001).

16. Koenig, S., Liu, Y.: “Terrain Coverage with Ant Robots: A Simulation Study”, AGENTS’01,

May 28–June 1, Montreal, Quebec, Canada, (2001).

17. Rekleitisy, I., Lee-Shuey, V., Peng Newz, A., Chosety, H.: “Limited Communication, Multi-

Robot Team Based Coverage”, Proceedings of the 2004 IEEE International Conference on

Robotics and Automation, New Orleans, LA, April, (2004).

18. V.Breitenberg: Vehicles, MIT Press (1984).

19. Y.Altshuler, I.A.Wagner, A.M. Bruckstein: “On Swarm Optimality In Dynamic And Sym-

metric Environments”, Second International Conference on Informatics in Control, Automa-

tion and Robotics (ICINCO), the First International Workshop on Multi-Agent Robotic Sys-

tems (MARS), pp. 64–71, Barcelona, Spain, (2005).