
Cooperative Multi-Agent Approach to Dynamic
Coverage in Multi-Robot Activities
Satoshi Kataoka
1
and Shinichi Honiden
The University of Tokyo,2-1-2 Hitotsubashi, Chiyoda-ku,Tokyo 101-8430, Japan
Abstract. Dynamic coverage is a problem of multi-robot systems based on wire-
less ad-hoc networks. The issue of dynamic coverage occurs notably in post-
disaster survivor rescue, search operation, and planet exploration. In this paper,
we introduce an novel algorithm of dynamic coverage in a realistically restricted
environment for robots.
1 Introduction
We address the problem of deploying a mobile sensor network into an environment with
the task of maximizing sensor coverage of the environment. We restrict ourselves to the
case where every node in the network is a mobile robot. All the robots can calculate
their own the position by dead reckoning and/or GPS (Global Positioning System). All
the robots have wireless communication facilities. Our proposal claims that the robots
make the field search as robustly and efficiently as they can in the range which they
do not miss each other. Our system is mainly made based on two approaches, Multi-
Agent-System and Dynamic and Distributed Voronoi Diagram. .The first one is the
Multi-Agent-System approach.
2 Related Works
Exploration and map building by multi robots in an unknown environments has benn
studied[1]. Although [1] is efficient, the devices of beacon are needed for others with
the robot which searches. And Voronoi Diagram is the algorithm often used in a sensor
coverage problem, and hos been studied by several authors[2,3].
3 Definition of Coverage Problem Solution
In this section we present a formal description of the planar boundary coverage problem
and provide high efficient solution of the problem compared with the existing research.
We then provide a solution based on Voronoi Overlay, with complexity (n log n), as-
suming that all the robots in the network have the sensing range which is defined for
every robot and knows its own range with each robot. We also make the assumption
that each device knows its two dimensional location. This is a reasonable assumption
since in the absence of this information, the boundary of coverage cannot be uniquely
Kataoka S. and Honiden S. (2006).
Cooperative Multi-Agent Approach to Dynamic Coverage in Multi-Robot Activities.
In Proceedings of the 2nd International Workshop on Multi-Agent Robotic Systems, pages 93-98
DOI: 10.5220/0001224500930098
Copyright
c
SciTePress

determined (i.e., from topological information alone). Moreover, the technology of the
position acquisition system which does not need a global system is realizable. We now
formally describe the coverage of a device. And parameters which used in this paper
are defined below. We use the notation dist (p1; p2) to denote the Euclidean distance
between two points p1 and p2.
3.1 Definition
Definition 1 The communication range of a robot agent RA with planar coordinates
(x ,y) and sensing range R (which is graphically explained in Figure ??) is a disk with
center ( x, y)and radius R. R is the greatest range with which each robot can commu-
nicate. A robot determines the division which he should patrol within the limits of this
area. Moreover, in order that he may not separate with other robots completely, the
guarantee other robots are within the limits of this periodically is required.
Definition 2 The base position VP (voronoi position) of each robot agent on the field is
held for every robot agent, and determines a search area by VP. That is, each robot agent
collects the bases of other agents within the communication limits = R, and calculates
a search area using Voronoi Diagram. Each robot changes each base by negotiation.
Definition 3 The search area VA (voronoi area) of each robot agent on the field is
calculated by itself, and holds it. A robot searches by moving the inside of this area.
Moreover, a robot holds the information on the obstacle of the range which searched
once. Each robot determines this area using Voronoi Diagram from VP of each robot of
his communication within the limits.
Definition 4 Each agent has the obstacle information OI, and this information is up-
dated as it develops the field. By using this information, each agent calculates ignore
area ID dynamically so that its area in its duty may not be divided. That is, in this
agent’s ID, other agents calculate VA as if this agent did not exist. An agent can de-
termine ID for every renewal of obstacle information without other agents information.
With our algorithm, only from other agents’ VP and ID, each agent can predict other
agents’ VA and can determine his VA. Since each agent does not need to re-calculate
VP and ID for every request from other agents, he can hold down the amount of com-
munications to minimum.
Definition 5 VP changes with negotiations between each agent. A robot moves simi-
larly to change of VP until each robot agent’s VA is decided. That is, VP cannot change
by the width of the velocity VEL more than a robot’s top velocity. Therefore, the high-
est of the VEL of VP is restricted by MAXVEL (max velocity).And we define the move
vector of VP in one step as VVECTOR.
Definition 6 An EVALUATION VALUE is used in the case of VVECTOR determination.
Since each agent calculates VVECTOR based on the EVALUATION VALUE acquired
from other agents, an EVALUATION VALUE can interfere in other agents’ action. In
other words, negotiation is performed through an EVALUATION VALUE.
94

Definition 7 The Dynamic Coverage Problem Given a set of n robots in the plane, each
with a sensing range r, patrol a plane with a random obstacle and acquire the state of
the plane on real time. Figure ?? expresses figure-description of Coverage Problem.
And take notice of two points which the next raises. The first point EXPANDING TIME
is time until a robot’s area is spread and decided in the field to the maximum extent.
The other point PATROLLING TIME is time concerning a robot patrolling VA.
3.2 Solving the Coverage-Boundary Problem with Voonoi Overlays
We divide each robot’s area in his duty (A) for the field using voronoi overlays. The time
concerning a robot going round is proportional to VA. PATOROLLING TIME which
described our point is equal to the largest time of all robots. That is, making VA equal
as much as possible leads to improvement in PATROLLING TIME. Theoretical most
efficient PATROLLING TIME can be expressed as follows.
P T min =
Sa − So
Numa
(1)
Sa · · · sizeoffield
So · · · sizeof obstacles
Numa · · · numberofagents
Our purpose is moving VP (the greatest move width of VP is equal to MAXVEL)
so that PATROLLING TIME may be brought close to PTmin as quickly as possible.
And this time is just EXPANDING TIME by convergence of VP.
We developed new approach of Voronoi Overlay of dynamic and a complete distributed
type. This approach has the low amount of communications, and is efficient (EXPAND
TIME is small) compared with ordinary approach.
4 Architecture
The agent carried in each robot acts using a technique which is described below. More-
over, the technique is taking into consideration restrictions of a realistic robot which
stated by definition, and is the general-purpose thing which can set up each parameter.
4.1 Algorithm Description
Distributed and Dynamic Voronoi Overlay. As for each agent, each calculates its
VA. An agent takes only a disk of a radius R focusing on its VP into consideration in
that case. VA is calculated using Voronoi Overlay from VP of other robot agents who
are inside the disk. Although the agent besides a disk is disregarded here, since VA is
a set of the point that the agent is the nearest, even if it does not take a far point into
consideration, a bad influence does not give calculation of VA. And it becomes clear
also from the result of a simulation experiment that this thinking is right. Moreover,
95

by this, since it communicates only with other robots of communication within the
limits, there is no necessity of doing the communication work of multi-hop etc., and the
amount of communications can be stopped low.
The flow of VA calculation. Each agent calculates VA by the flow shown below. Si-
multaneously, the EVALUATION VALUE used in the case of negotiation with other
agents is also calculated.
Step 1 Obstacle Prediction
The agent predicts the obstacle of non-searched area by using from the obstacle infor-
mation and exploitation information in his communication area. And the agent deter-
mines the area which he divides.
Step 2 Information acquisition
The agent acquires VP and a ignore area ID from other agents within the communication
limits.
Step 3 Voronoi Overlay
The agent divides the area calculated at step2 by Voronoi Overlay using VP and ID
which were acquired at 1.
Step 4 Calculation of EVALUATION VALUE
An agent computes an EVALUATION VALUE using the size of VA and other agents’
VP which were acquired at step3. This value is used by the negotiation explained later.
5 Expelimental Result
We performed comparison with DDVAS which we developed, the existing distributed
approach (molecular algorithm), and the theoretical optimal value paying attention to
EXPANDING TIME and PATROLLING TIME which are two points shown in Cov-
erage Problem Definition. Moleculer Algorithm which is the existing research that we
compare doesn’t guarantee that PT becomes below fixed. So we cann’t measure spec for
every PT. Then, we measure PATOROLLING TIME and EXPANDING TIME of the
present Moleculer Algorithm and compare with the value. And each robot’s parameter
was divided into two portions, the parameter to fix and the parameter to change. The
fixed parameters are the things which we judged that it is realistic and it is not necessary
to make it change.
The fixed parameter is created based on the actual robot which is also used in mole-
culer algorithm. These parameters are fixed in order to prevent comparison of perfor-
mance becoming complicated, although it can change arbitrarily inside a program.
96
5.1 Performance Comparison of PATOROLLING TIME
We measured EXPANDING TIME for every PATOROLLING TIME using parameter
of Table 1. PATROLLING TIME is equal to the time concerning a robot with the biggest
area in his duty in a robot going round. We set EXPANDING TIME that is the time until
PATROLLING TIME becomes below the defined value (MAXPT). MAXPT is based
on the optimal value of PAOROLLING TIME and it can imagine easily that EXPAND-
ING TIME becomes smaller as MAXPT is large. So our approach has guaranteed that
PATROLLING TIME is below arbitrary values, when agents’ VD is converged. The
optimal value of PATROLLING TIME is equal to PTmin shown in Definition. We cal-
culated the time which it takes when a robot moves the optimal value of EXPANDING
TIME to the optimal arrangement in a straight line for every map. In 6.1 MAXPT is
changed, in 6.2 the number of agents is changed and in 6.3 a time step which is the time
of one cycle of agent action is changed. And the performance was compared every three
maps. We use the value which averaged the result which carried out the simulation 100
times in three different maps of which sizes are 500(m) × 500(m).The first map has no
obstacle,the second map has only one obstacle,and the last map has many obstacles.
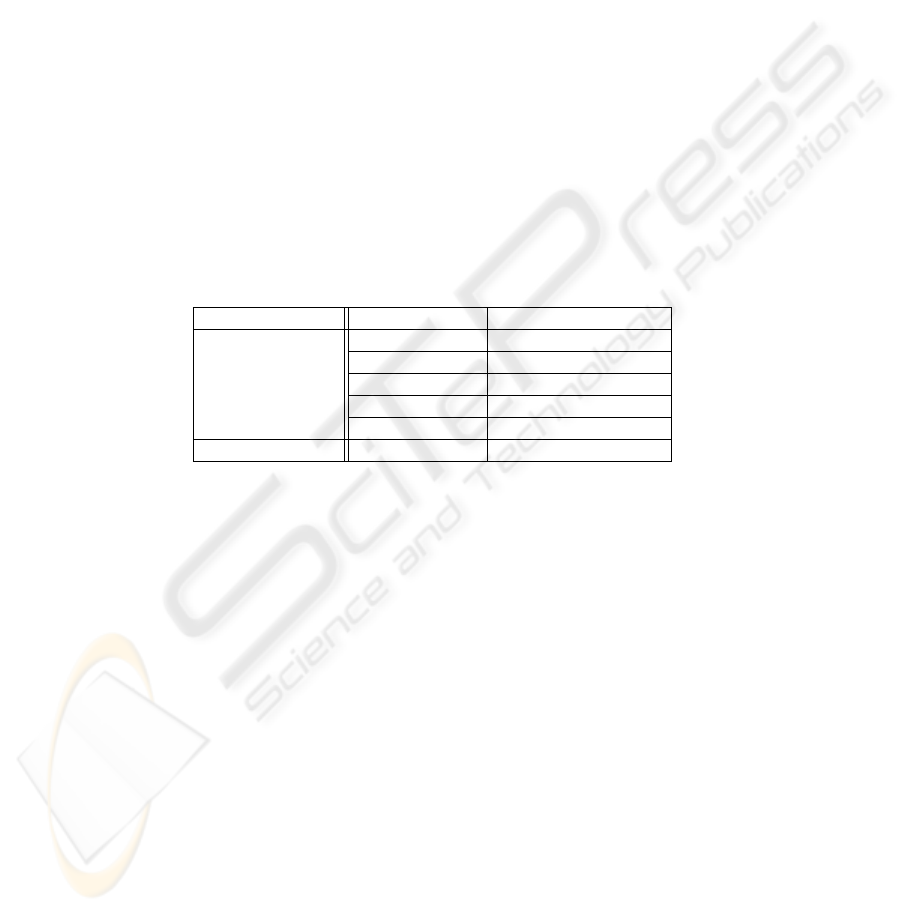
Table 1. Used Parameters in Comparison of PATOROLLING TIME.
type of parameter parameter name used value at this section
Fixed parameter
R 100(m)
MAXVEL 1(m/s)
map size 500(m) × 500(m)
Number of Robots 10(robots)
Time Step 10(s/cycle)
Changing parameter MAXPT 105% ∼ 200%
Although the number of agents is fixed in 10 here, comparison of this change is
performed.
Result shows that DDVAS shows the outstanding performance compared with mole-
cular algorithm. However, the difference with the optimal value is large as map becomes
complicated. And, as expected, EXPANDING TIME becomes small as MAXPT be-
comes large.
According to simulation,EXPANDING TIME is large when time step is large. There-
fore, as for a time step, it is desirable to make it as small as possible.
6 Conclusions
We have presented a novel distributed solution for solving Dynamic Coverage Problem
that is based on a multi-agent system. In our approach, each robot can act intellectu-
ally, without needing the server of central control. We are making each agent control a
97

Fig.1. Comperison of PATOROLLING TIME.
motion of each robot, and have realized performance superior to the conventional ap-
proach. Moreover, we verified that this approach was also excellent also in robustness
as a multi-robot system.
7 Future Work
We introduced the distributed and dynamic approach using Voronoi Overlay for Cov-
erage Problem of strange area. However, still, the environment which we defined is
not realistic enough. As first inadequate point, the environment which we assumed is
2D. Naturally the place where a robot works is 3D. Therefore, it is necessary to bring
close more nearly actually by making environment into 3D (a hill, a mountain, etc).
As second inadequate point, an unreal point is that it is completely the same in each
robot’s performance. A robot is considered that each performance (max velocity, com-
munication range, etc) changes according to his feature. Therefore, we should do the
simulation which also took the difference of an each object into consideration. As third
inadequate point, it is that many room for EXPANDING TIME to approach the optimal
value is left behind.
References
1. Maxim A. Batalin, Gaurav S. Sukhatme: Multi-robot Dynamic Coverage of a Planar Bounded
Environment,CRES-03-011, 2003
2. Seapahn Meguerdichian, Farinaz Koushanfar, Miodrag Potkonjak, Mani B. Srivastava: Cov-
erage Problems in Wireless Ad-hoc Sensor Networks, INFOCOM,2001
3. Carbunar, Grama, Vitek: Distributed, Dynamic Voronoi Overlays for Coverage Detection, Dis-
tributed Hash Tables in Ad-Hoc Networks ICPADS, 2004
98
