Comparison of Approximate Entropy Measure and

Poincaré Plot Indexes for the Study of Gait

Characteristics in the Elderly

Ahsan H. Khandoker

, Marimuthu Palaniswami

, and Rezaul K. Begg

Department of Electrical & Electronic Engineering, The Universityof Melbourne,VIC

3010,Australia

Biomechanics Unit, Centre for Ageing, Rehabilitation, Exercise and Sport, Victoria

University, VIC 8001,Australia

Abstract. Early identification of at-risk gait helps prevent falls and injuries.

The aim of this study is to investigate the relationship between approximate en-

tropy (ApEn) and Poincaré plot indexes of elderly gait patterns and to test

whether ApEn could be used as a reliable gait identifier for falls-risk. Minimum

foot clearance (MFC) data of 14 elderly and 10 elderly participants with a his-

tory of falls and balance problems were analyzed. The ApEn values of MFC

were significantly correlated with Poincaré plot indexes of MFC in the healthy

elderly group, whereas correlations were absent in the elderly fallers group.

Mean ApEn in the fallers group (0.18±0.03) was significantly higher than that

in the healthy group (0.13±0.13). The higher ApEn values in the fallers group

might indicate increased irregularities in their gait patterns and a loss of gait

control mechanism. Results are useful for the early diagnosis of common gait

pathologies.

1 Introduction

It has been well documented in the literature that ageing influences gait patterns that

affects the control mechanism of human locomotor balance. One major aim of study-

ing gait characteristics is to identify gait variables that reflect gait degeneration due to

ageing with linkages to the causes of falls. This would help to undertake appropriate

measures to prevent falls.

Approximate entropy (ApEn), a mathematical approach to quantify the complexity

and regularity of a system, has been introduced by Pincus [1], based on a novel sys-

tematic biological theory [1,2]. Such theory has suggested that healthy dynamic sta-

bility arises from the combination of specific feedback mechanisms and spontaneous

properties of interconnected networks, and the weak connection between systems or

within system is the mechanism of disease, which is characterized by an increased

irregularity of the time series [2]. Therefore, ApEn was considered to provide a di-

rect measurement of feedback and connection, and a low ApEn value often indicates

H. Khandoker A., Palaniswami M. and K. Begg R. (2006).

Comparison of Approximate Entropy Measure and Poincaré Plot Indexes for the Study of Gait Characteristics in the Elderly.

In Proceedings of the 2nd International Workshop on Biosignal Processing and Classiﬁcation, pages 144-151

DOI: 10.5220/0001225701440151

 SciTePress

predictability and high regularity of time series data, whereas a high ApEn value

indicates unpredictability and random variation [2]. Previous studies [7] on the en-

tropy of human gait in multiple scale discussed the scaling effect of entropy on vari-

ous walking patterns, indicating the changes of multiscale entropy values with slow,

normal and fast walking.

Poincaré plot is a geometrical representation of a time series into a Cartesian plane,

where the values of each pair of successive elements of the time series define a point

in the plot. Indexes derived from Poincaré plot of minimum foot clearance (MFC)

were used to classify young-old gait types in our previous study [6].

In order to test whether the ApEn of MFC variability could be used as a better

identifier of gait pathologies or not, we apply ApEn analysis method to the MFC gait

data obtained from elderly subjects with and without having balance problem, and

compare the results with those obtained with Poincaré plot indexes analysis.

2 Gait analysis

2.1 MFC Gait data

Minimum foot clearance (MFC) data from 14 healthy elderly (mean age: 62 years)

and 10 elderly with a history of falls (mean age: 63.2 years) were taken from Victoria

University (VU)’s Biomechanics Unit database. Foot clearance (FC) data for these

subjects were collected during their steady state self-selected walking on a treadmill

using a PEAK MOTUS 2D motion analysis system (Peak Technologies Inc, USA).

Minimum foot clearance (MFC) was calculated by subtracting ground reference from

the minimum vertical coordinate during the swing phase through a 2D geometric

model [9].

2.2 Estimation of ApEn of MFC

ApEn is defined as the logarithmic likelihood that the patterns of the data that are

close to each other will remain close for the next comparison within a longer pattern.

ApEn is computed by using the following equation:

where C, N, r, and m represent the correlation integral, the total number of data points

in the MFC time series, vector comparison length, and embedding dimension, respec-

tively. In the ApEn calculation with our MFC data, N was fixed at 400 points and m

at 2. The tolerance r was chosen as 40% of the SD of the MFC data points and C was

the number of vectors with a maximum distance less than or equal to r to the template

()

∑

+−=

−−

−

)1m(N

)r(Cln1mN)r,m,N(ApEn

∑

−−

−

)r(Cln)mN(

145

vector. The natural logarithm of C was averaged over the 400 stride numbers and this

process was repeated for m=3. ApEn was defined as the difference between the val-

ues calculated using m=2 and m=3.

2.3 MFC Poincaré plots

MFC data plots between successive gait cycles, i.e., between MFCn and MFCn+1

(see Figure 1B,D), known as MFC Poincaré plots [6], shows variability of MFC data

and describes performance of the locomotor system in controlling the foot clearance

at this critical event. Poincaré plots with high correlation coefficient is attributed to

high level of control between strides, whereas a low correlation shows less control

since one stride is loosely affected by the previous stride. These plots were used to

extract indexes, such as length (SD2) and width (SD1) of the long and short axes of

Poincaré plot images [3]

. The width of this plot corresponds to the level of short-term

variability, while the length of the plot corresponds to the level of long-term variabil-

ity.

3 Results

In order to compare the gait patterns of healthy elderly and falls-risk elderly, two

representative examples of MFC time series and its corresponding Poincaré plots

taken from each group have been presented in figures 1A,B,C&D. Gait characteristics

of a healthy elderly subject with mean MFC (1.56 ± 0.21cm), and its corresponding

Poincaré plot (Fig.1B) with indexes (SD1=0.31, SD2= 0.5, SD1/SD2=0.63) and esti-

mated ApEn (0.15) seemed quite different from the gait characteristics of falls-risk

elderly subject with mean MFC (1.71±0.41cm), and its corresponding Poincaré plot

(Fig.1D) with indexes SD1=0.72, SD2= 0.92, SD1/SD2=0.79) and estimated ApEn

(0.21). Student’s t-test showed that average values of mean MFC, sdMFC, SD1,

SD2, and ApEn in healthy elderly group are significantly different from those in the

falls-risk elderly group (P<0.05) ( Table 1 &2).

3.1 Relationship between ApEn and mean MFC

Table 1 & 2 show the Pearson correlation matrices among all tested indexes in the

healthy elderly group and falls-risk elderly group. The correlation coefficient of mean

MFC with ApEn is significantly (P<0.05, student t-test) higher in the falls-risk group

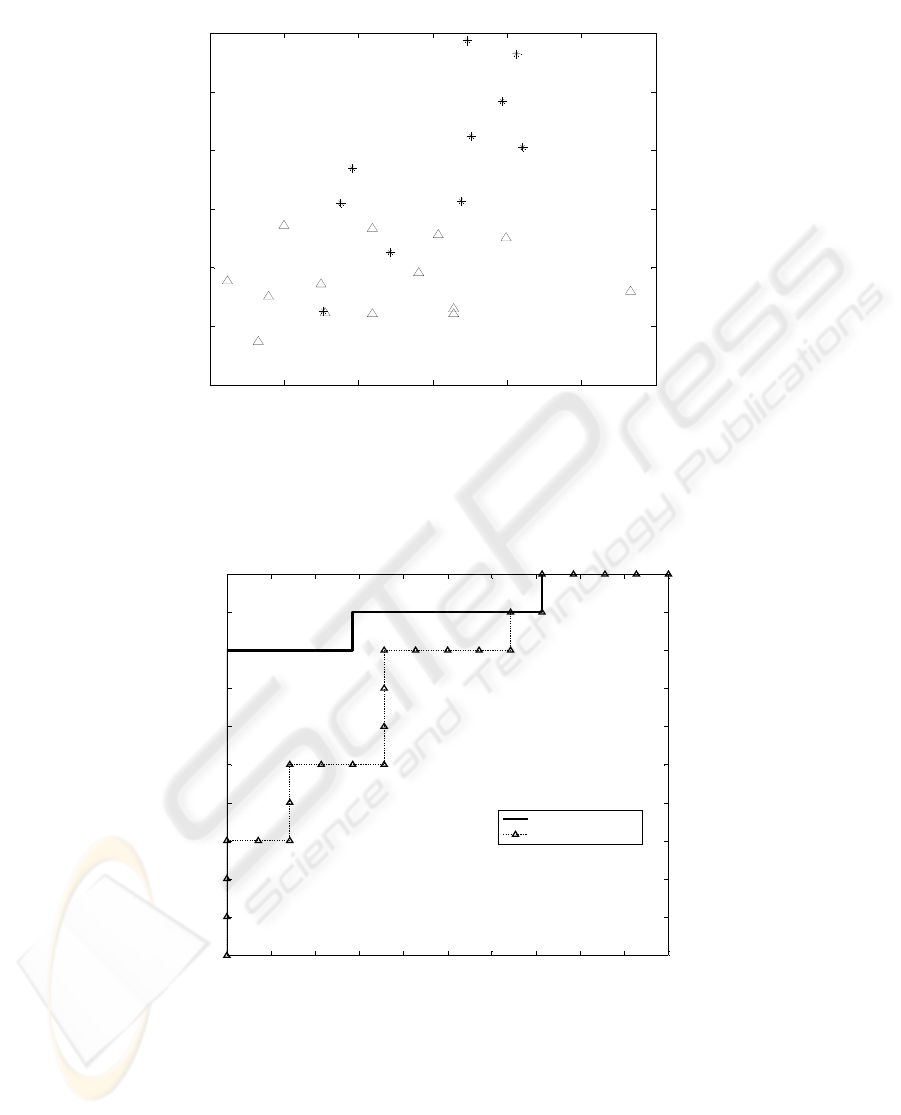
(0.74) compared to that in the healthy group (0.14). Figure 2 illustrates a positive

correlation between ApEn and mean MFC measures within the fallers group, how-

ever, such correlation was absent in the healthy elderly group.

146

Fig. 1. Top panels show MFC time series from a healthy elderly subject (A) and its corre-

sponding poincaré plot (B). Bottom panels show MFC time series from an elderly subject with

balance problem (C) and its corresponding poincaré plot (D).

3.2 Relationship between ApEn and Poincaré plot indexes

Correlation analysis also shows that ApEn was significantly correlated with Poincaré

plot indexes (SD1, SD2), however not with the SD1/SD2 ratio in the healthy elderly

group. No significant correlation was found between ApEn and Poincaré plot indexes

in the fallers group.

3.3 ROC curve analysis

Receiver Operating Characteristics (ROC) curves were used to characterize the qual-

ity of the single MFC indexes with respect to the identification task. Table 3 summa-

rizes the ROC areas calculated for each index. The larger area under ROC curve indi-

cates better performance of that classifier. The largest ROC area (0.90) was found for

ApEn, whereas the lowest area (0.55) was for SD1/SD2 ratio. In order to show the

comparative performance of ApEn and SD2 as a gait pattern identifier, ROC curves

for ApEn and SD2 were plotted (see Fig. 3).

0 100 200 300 400

0.5

1.5

2.5

3.5

Stride number

Minimum foot clearance (MFC) (cm)

MFC+1

MFC

Minimum foot clearance (MFC) (cm)

MFC

MFC+1

Stride number

0 0.5 1 1.5 2 2.5 3 3.5

0.5

1.5

2.5

3.5

0 100 200 300 400

0.5

1.5

2.5

3.5

0 0.5 1 1.5 2 2.5 3 3.5

0.5

1.5

2.5

3.5

A B

SD2

SD1

147

0.5 1 1.5 2 2.5 3 3.5

0.1

0.12

0.14

0.16

0.18

0.2

0.22

Mean MFC (cm)

Approximate entropy

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

False positive

True positive

Approximate entropy

Poincare length

Fig. 2. Scatter plot for ApEn vs mean MFC for the healthy elderly subjects (Δ) and the elderly

subjects with balance problem (*). Note: good separation between healthy and non healthy

subjects with clustering of points in two distinct “clouds”. Correlation coefficients between

ApEn and mean MFC for the two groups were 0.14 (Δ )and 0.74 (*) respectively. (Table 1 &

2).

Fig. 3. ROC (receiver operating characteristics) curves showing true positive (sensitivity) and

false positive rate (1-specificity) for various thresholds using Approximate entropy (ApEn)

and length of the Poincaré plots (SD2) across 14 healthy elderly subjects and 10 elderly sub-

148

jects with balance problem. Areas of ROC curves for ApEn and SD2 were 0.9 and 0.73 respec-

tively. (Table 3).

Table 1. Correlation coefficients among mean MFC, Poincaré plot indexes and ApEn of MFC

in the healthy elderly subjects (n= 14).

Table 2. Correlation coefficients among mean MFC, Poincaré plot indexes and ApEn of MFC

in the elderly with balance problem (n=10).

Table 3. ROC areas for ApEn and Poincaré plot indexes.

4 Discussion

The results of this study suggest that ApEn analysis of MFC data provides useful

information regarding identification of gait characteristics in the elderly. Early detec-

tion of gait pattern changes due to ageing and falls-risk using a nonlinear index like

ApEn might provide the opportunity to initiate pre-emptive measures to be under-

Mean

MFC

SD1

SD2

SD1/

SD2

ApEn

Mean

±sd

1.65

±0.75

0.35

±0.13

0.51

±0.19

0.89

±0.32

0.64

±0.13

0.13

±0.13

mean MFC 1 0.31 0.51 0.21 0.38 0.14

sd MFC 1 0.90*** 0.99*** -0.36 -0.73**

SD1 1 0.81** 0.082 -0.58*

SD2 1 -0.50 -0.74**

SD1/SD2 1 0.38

ApEn 1

* P<0.05 ** P<0.01 *** P<0.001 SD1= Poincaré width,

SD2= Poincaré length, sd=standard deviation

Mean

MFC

SD1

SD2

SD1/

SD2

ApEn

Mean

±sd

2.01

±0.51

0.48

±0.16

0.72

±0.25

1.15

±0.40

0.64

±0.12

0.18

±0.03

mean MFC 1 0.85*** 0.70* 0.86** -0.44 0.74*

sd MFC 1 0.90*** 0.99*** -0.37 0.58

SD1 1 0.81** 0.06 0.49

SD2 1 -0.51 0.59

SD1/SD2 1 -0.28

ApEn 1

* P<0.05 ** P<0.01 *** P<0.001 SD1= Poincaré width

SD2= Poincaré length sd=standard deviation

mean

MFC sd MFC SD1 SD2

SD1/SD2 ApEn

ROC area 0.71 0.74 0.76 0.73 0.55 0.9

149

taken to avoid injurious falls. Also, such nonlinear index could potentially be used as

gait diagnostic parameter in clinical situation.

In this study, MFC data from steady-state gait have been used to characterize gait

patterns. There are two major reasons for this. Firstly, MFC provides a more sensitive

measure of motor function of the locomotor system compared to some gross overall

kinematic descriptions of gait such as joint angular changes or stride phase times,

secondly its close linkage with tripping falls [8]. Furthermore, long-term MFC data,

as used in this study, are required so that variability indexes of MFC having long

range correlation could be

captured representative of the real gait performance.

Our results suggest that gait pathologies with falls and balance problems are re-

flected in Poincaré plots and features extracted from these plots are effective in dif-

ferentiating between healthy and falls-prone gaits. Poincaré plots were used in our

earlier study for young-old gait classification [6]. In this study, such analysis has been

extended to identifying elderly with a history of falls and balance problems. More-

over, nonlinear parameter like ApEn has been applied in this study in identifying gait

characteristics. Although both Poincaré plot indexes and ApEn were effective in

discriminating the gait characteristics patterns, results of our present study suggest

that ApEn could perform better than Poincaré plot indexes in identifying gait pattern.

One possible reason why a nonlinear index like ApEn could be a more effective gait

identifier might be that physiologic control mechanism of healthy human gait is

nonlinear and correlated. However, higher ApEn values displayed in the fallers group

might be an indication of the breakdown of locomotor control mechanism in the falls-

risk elderly. ApEn reflects irregularity, randomness and complexity of the MFC time

series data, and would therefore, indicate the stability in the control of foot motion

over the ground.. In a previous study involving gait, Costa et al [7] applied multi-

scale entropy (MSE) for analysing gait with different speeds and studied the scaling

effect on sample entropy for different walking rates. Sample entropy (SampEn) on

single scale in a healthy walking time series was found to be the lowest value in that

study [7]. Although both SampEn and ApEn quantify the regularity of a time series,

methods of calculation are different [5]. However, ApEn results of this study sug-

gests that the pathologic gait having higher ApEn is more random than healthy physi-

ologic gait having lower ApEn. Nonlinear index like ApEn which probe a dynamical

property of human gait control, has, therefore, implications for quantifying and mod-

elling gait control under various conditions. Further investigation should be carried

out to derive additional nonlinear variability indexes of human gait.

Acknowledgements

MFC gait data for this study were taken from VU Biomechanics Unit. Several people

have contributed to the creation of the gait database, especially Simon Taylor of the

VU Biomechanics Unit.

150

References

1. Pincus SM, Goldberger AL, : Physiological time-series analysis: what does regularity

quantify? Am J Physiol, (1994) 266:H1643-H1656.

2. Pincus S: Approximate entropy (ApEn) as a complexity measure. Chaos , (1995) 5:110-

117.

3. Brennan, M., Palaniswami, M. and Kamen, P.W.: Do existing measures of Poincaré plot

geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng.,

(2001) vol. 48, pp. 1342-1347.

4. R. J. Best, R. K. Begg, and L. Dell’Oro: The probability of tripping during gait. Int. Soc.

Biomech. Conf., (1999) Calgary, AB, Canada.

5. Richman JS, Moorman JR: Physiological time series analysis using approximate

entropy and sample entropy. Am J Physiol Heart Circ Physiol, (2000) 278: H2039-H2049.

6. Begg R.K, Palaniswami M., and Owen B.: “Support vector machine for automated gait

classification. IEEE Trans. Biomed. Eng., (2005) vol. 52, No. 5 pp. 828-837.

7. Costa M, Peng C-K, Goldberger AL, Hausdorff JM.: Multiscale entropy analysis of human

gait dynamics. Physica A (2003);330:53-60.

8. Winter, D. : The Biomechanics and Motor Control of Human Gait: Wormal, Elderly and

Pathological.Waterloo: University of Waterloo Press (1991).

9. Begg RK, Best RJ, Taylor S & Dell'Oro L:Minimum foot clearance during walking:

Strategies for the minimization of trip-related falls. In Press (2006) Gait and Pos-

ture.

151