DATA MINING METHODS FOR GIS ANALYSIS

OF SEISMIC VULNERABILITY

Florin Leon

Faculty of Automatic Control and Computer Science, ”Gh. Asachi” Technical University, Bd. Mangeron 53, Iaşi, Romania

Gabriela M. Atanasiu

Faculty of Civil Engineering, ”Gh. Asachi” Technical University, Bd. Mangeron 43, Iaşi, Romania

Keywords: Data mining, Geographic Information Systems, Supervised clustering, k-Nearest Neighbor, Seismic risk

management.

Abstract: This paper aims at designing some data m

ining methods of evaluating the seismic vulnerability of regions in

the built infrastructure. A supervised clustering methodology is employed, based on k-nearest neighbor graphs.

Unlike other classification algorithms, the method has the advantage of taking into account any distribution of

training instances and also data topology. For the particular problem of seismic vulnerability analysis using a

Geographic Information System, the gradual formation of clusters (for different values of k) allows a decision-

making stakeholder to visualize more clearly the details of the cluster areas. The performance of the k-nearest

neighbor graph method is tested on three classification problems, and finally it is applied to a sample from a

digital map of Iaşi, a large city located in the North-Eastern part of Romania.

1 INTRODUCTION

Given the costs of natural and technological disasters,

there is a clear need for measurement and evaluative

techniques that enable efficient resource allocation for

decision-making stakeholders. A key concept for the

evaluation of vulnerability, developed primarily for

seismic events, is the fragility curve. Fragility curves

(or damage functions) are used to approximate

damage due to natural hazards, i.e. fragility is a

measure of vulnerability or estimation of overall risk.

Fragility functions can be developed using

fferent methods, heuristic, empirical, analytical or a

combination of two methods. Heuristic functions are

developed using the consensus opinion of Structural

Engineering experts with years of experience

designing various types of structures and observing

the behavior of such structures for past earthquakes.

Empirical functions are based on observed data, while

analytical damage functions are based on modeling

the idealized structural behavior for different

constructions (Norton & Abdullah, 2004).

Fragility curves can be used for modeling the

effect

s of a possible natural hazard event, as a method

of analyzing the behavior of built infrastructure under

different scenarios, in order to minimize the effects of

an actual catastrophic incident. Because of the

complexity of the spatial information involved, one

needs an automatic method to efficiently investigate

the overall vulnerability of an area. The fragility curve

is a mathematical expression that relates the

conditional probability of reaching or exceeding a

particular damage state, given a particular level of a

demand or hazard (Simpson et al., 2005). HAZUS

(National Institute for Building Sciences, 2001)

specifies four damage states: slight, moderate, severe,

and complete damage state.

Data mining or knowledge discovery in databases

the process of search for valuable information in

large volumes of data, exploration and analysis, by

automatic or semi-automatic means, of large

quantities of data in order to discover meaningful

patterns and rules (Fayyad, Piatetsky-Shapiro &

Smyth, 1996).

This paper aims at designing some data mining

ethods in order to evaluate the seismic vulnerability

of regions in the built infrastructure, using as case

study an example from Iaşi, a large city of Romania

(Atanasiu & Leon, 2006).

153

Leon F. and M. Atanasiu G. (2006).

DATA MINING METHODS FOR GIS ANALYSIS OF SEISMIC VULNERABILITY.

In Proceedings of the First International Conference on Software and Data Technologies, pages 153-156

DOI: 10.5220/0001308301530156

 SciTePress

2 NNGE CATEGORIZATION

The data mining problem implies analyzing a set of

points defined as geographic coordinates x and y and

their damage or risk level r. Depending on the

considered approach, the risk can be nominal, which

means that each building belongs to a certain risk

class C

, or numerical, i.e. each building has a risk

probability associated with it, a real number

. The goal is to find the subsets of nearby

points, clusters, which share the same C

]1,0[∈r

, or at least

clusters with minimum impurity, i.e. most of the

cluster members should belong to the same class or

have close r values.

A straightforward approach is to use a

categorization algorithm to describe such subsets of

points. In general, categorization is a task of finding a

target function f that maps each attribute set A that

defines an object into one (or more, each with a

degree of membership) predefined class C. This target

function f is also known as the categorization or

classification model.

In the literature (Tan, Steinbach & Kumar, 2005;

Han & Kamber, 2000; Mitchell, 1997; Nilsson, 1996)

several categorization types of algorithms are

described. Among the most frequently used are rule-

based methods, prototype-based methods and

exemplar-based methods.

For the particular purpose of our research, the

rule-based categorization seems to be most

appropriate, since we need a non-hierarchical, explicit

partition of data. A nearest-neighbor-based approach

is useful, because the prediction phase is irrelevant in

our case. The damage of the building cannot be

predicted by taking into account only the damage of

its neighbors. Also, this class of algorithms always

performs well on the training set, with error rates

close to 0.

Such an algorithm is the Non-Nested Generalized

Exemplar, NNGE (Martin, 1995; Witten & Frank,

2000), which forms homogenous hyper-rectangles

(generalized exemplars) in the attribute space such

that no exception should be contained within. The

hyper-rectangles do not overlap, and in this way, the

algorithm prevents over-fitting.

In order to test the behavior of the algorithm we

used a test problem proposed by Eick, Zeidat, and

Zhao (2004), displayed in figure 1, where different

point colors represent different classes.

The results of NNGE algorithm are presented in

the same figure. One can see the hyper-rectangles

found by the algorithm, which are 2-D rectangles in

our case. In addition, the convex hull of the cluster

points is emphasized and the internal area of the

convex hull is hatched.

Figure 1: NNGE results for the test problem.

The algorithm only discovers axis-parallel hyper-

rectangles; it cannot take into account other

distributions of data. Another disadvantage is that

NNGE can link rather distant points, if there is no

exception example lying between them.

An alternative approach is to use a clustering

method instead of classification, which should also

use the predefined r values of points.

3 K-NEAREST NEIGHBOR

GRAPH METHOD OF

SUPERVISED CLUSTERING

The goal of the cluster analysis is to group the

instances based only on information found in the data

that describes the objects and their relationships, i.e.

their attributes. Objects within a group should be

more similar or related to each other than to objects

from other groups. The greater the similarity (or

homogeneity) within a group and greater the

difference between group, the better the clustering.

There are many clustering algorithms known in the

literature: hierarchical (nested) vs. partitional (un-

nested), exclusive vs. overlapping or fuzzy, complete

vs. partial (Tan, Steinbach & Kumar, 2005).

Clustering is typically applied in an unsupervised

learning framework using particular error functions,

e.g. an error function that minimizes the distances

inside a cluster, therefore keeping the clusters tight.

An unsupervised approach for the problem

presented in figure 1 would most likely lead to

clustering together all the points in the upper region,

because they are closer to each other from the

topological point of view, even if they belong to

different classes.

Supervised clustering, on the other hand, deviates

from traditional clustering since it is applied on

classified examples with the objective of identifying

clusters that have high probability density with

respect to single classes (Eick, Zeidat & Zhao, 2004).

For our problem, we propose a clustering method

that simultaneously takes into account the topology of

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

154

instances and their established r values. The algorithm

is simple: every instance is linked to its nearest

neighbor or to its k-nearest neighbors with the same

class or close r values. The links formed in such a

way determine several graphs in the instance set. The

graphs of directly or indirectly connected points are

the clusters one needs for our purpose.

Figure 2 shows the results for the same problem,

for different values of k. The convex hull of the

cluster points is also displayed and its interior area is

hatched.

When k increases, so does the average size of the

clusters. The iterative process is useful for a decision-

maker in order to capture details at different levels of

complexity. The clustering results are useful only up

to a point (usually between 2 and 4). When k is 1, the

number of graphs is large and the clusters seem

disconnected. When k is large, all the points of a class

tend to be connected and the local topology

information gets lost.

4 GIS-BASED ANALYSIS OF

SEISMIC VULNERABILITY OF

BUILT INFRASTRUCTURE

Zoning of hazard prone regions is a common practice.

The vulnerability of existing classes of buildings,

other critical structures and population is dependent

on their exposure to the hazard, which varies from

location to location. The spatial characteristics of

hazard and vulnerability justify the application of

mapping and spatial technologies such as GIS in the

risk assessment process.

Figure 2: k-NN graph results for k=1 (top left), k=2 (top

right), k=3 (bottom left), and k=8 (bottom right).

Figure 3: GIS-based vulnerability map.

A widely accepted definition of GIS is the

following: “a Geographical Information System is an

organized collection of hardware, software

geographical data and personnel designed to

efficiently capture, store, update manipulate, analyze

and display all forms of geographically referenced

information” (Lavakare & Krovvidi, 2001).

Figure 4: NNGE cluster map.

Figure 5: Cluster map for k-NN graph with k=3 and

categorical distances.

From the digital map of Iaşi one can consider a

detail, where the constructions are colored depending

DATA MINING METHODS FOR GIS ANALYSIS OF SEISMIC VULNERABILITY

155

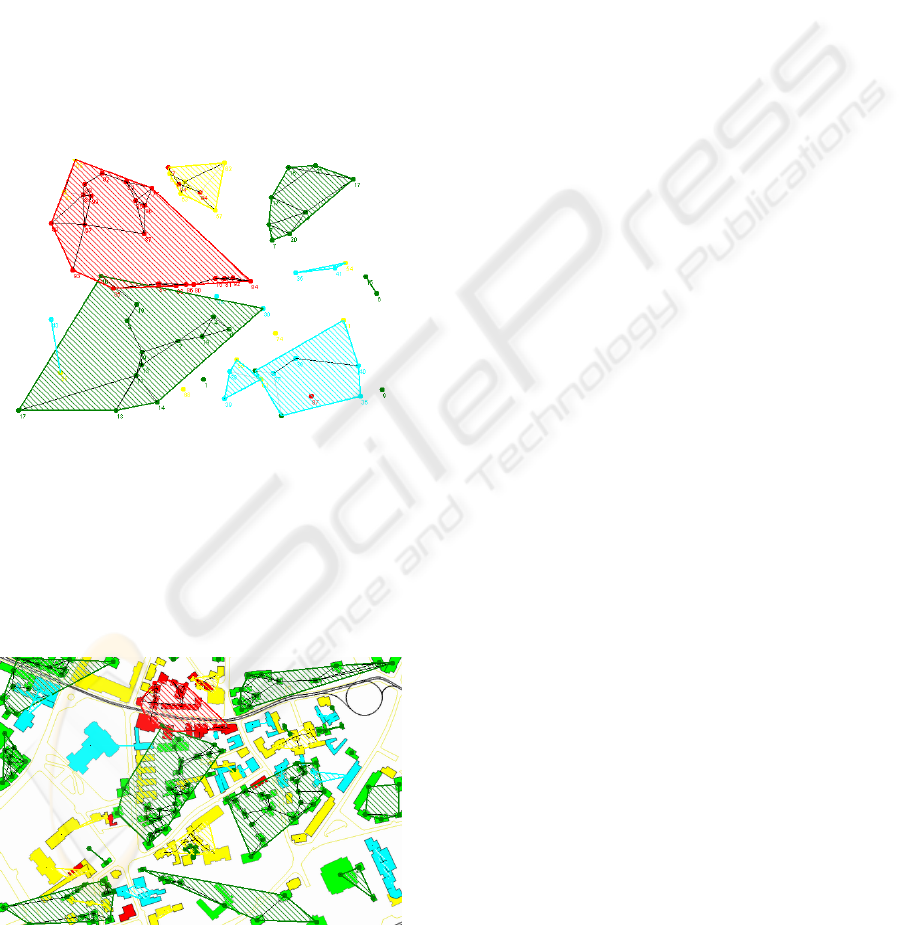
on their r value as shown in figure 3: green stands for

minor damage, cyan means moderate damage, yellow

represents major damage, and red stands for near-

collapse.

Figure 4 shows the cluster map provided by

NNGE. Figure 5 shows the results of k-NN graph

with k=3 and categorical distances, i.e. links are only

considered between instances that belong to the same

class C

. The number associated with each instance is

the cluster number that the object belongs to.

In figure 6 a similar result is presented. In this case

a link is drawn between nearby instances only if the

absolute value of the difference between their r values

is smaller than one definite value ε. In this example

we considered ε = 0.25. The number associated with

each instance represents the r value, in percents.

Figure 6: Cluster map for k-NN graph with k=3 and

real number distances.

Based on the above described methodology, these

results can be later superposed on the regular GIS

map, giving the decision-making stakeholder a

graphical suggestion about the spatial clusters among

building classes with buildings that belong to the

same risk or damage class (figure 7).

Figure 7: Spatial clusters of vulnerability classes on a GIS

map.

5 CONCLUSIONS

The method presented here proves to be useful to

identify the clusters of constructions on the urban

built infrastructure taking into account the classes of

seismic vulnerability.

A future research direction would be to add a

weighting mechanism to the instances, depending for

example on the area of the building or on its

importance.

REFERENCES

Atanasiu, G. M., Leon, F., 2006. Spatial Infrastructure

Information (SII) Based Management for Seismic

Vulnerability of Built Urban Fund. Research Grant

3202 Report, CEEX Program.

Eick, C. F., Zeidat, N., Zhao, Z., 2004. Supervised

Clustering – Algorithms and Benefits. In Proc.

International Conference on Tools with AI (ICTAI),

Boca Raton, Florida, pp. 774-776.

Fayyad, U. M., Piatetsky-Shapiro, G., Smyth, P., 1996.

From Data Mining to KnowledgeDiscovery: An

Overview. In Advances in Knowledge Discovery and

Data Mining, AAAI Press, Menlo Park, pp. 1 – 34.

Han, J. Kamber, M., 2000. Data Mining: Concepts and

Techniques. The Morgan Kaufmann Series in Data

Management Systems, Morgan Kaufmann Publishers.

Lavakare, A., Krovvidi, A., 2001. GIS & Mapping for

Seismic Risk Assessment. National seminar on Habitat

Safety against Earthquakes and Cyclones, New Delhi.

Martin, B., 1995. Instance-Based Learning: Nearest

Neighbour with Generalisation, Master of Science

Thesis, University of Waikato, Hamilton, New Zealand.

Mitchell, T.M., 1997. Machine Learning, McGraw Hill.

National Institute for Building Sciences, 2001. Earthquake

loss estimation methodology HAZUS99 SR2, Technical

manuals I-III National Institute for Building Sciences,

Washington, DC.

Nilsson, N. J., 1996. Introduction to Machine Learning.

Stanford University, http://ai.stanford.edu/people/

nilsson/mlbook.html.

Norton, T.R., Abdullah, M.M., 2004. Combined Hurricane

and Earthquake Hazard Component Vulnerability

Analysis. 2004 ANCER Annual Meeting: Networking of

Young Earthquake Engineering Researchers and

Professionals, Honolulu, Hawaii.

Simpson, D. M., Rockaway, T. D., Weigel, T. A., Coomes,

P. A., Holloman, C. O., 2005. Framing a new approach

to critical infrastructure modelling and extreme events.

International Journal of Critical Infrastructure Systems,

Vol. 1, Nos. 2/3.

Tan, P.N., Steinbach, M., Kumar, V., 2005. Introduction to

Data Mining. Addison Wesley.

Witten, I. H., Frank, E., 2000. Data Mining: Practical

machine learning tools with Java implementations,

Morgan Kaufmann, San Francisco.

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

156