ON THE EVALUATION OF TREE PATTERN QUERIES

Yangjun Chen

Department of Applied Computer Science, University of Winnipeg

Winnipeg, Manitoba, Canada R3B 2E9

Keywords: XML document, Tree pattern queries, Tree embedding, Constraint satisfaction problem, NP-complete.

Abstract: The evaluation of Xpath expressions can be handled as a tree emb

edding problem. In this paper, we propose

two strategies on this issue. One is ordered-tree embedding based and the other is unordered-tree embedding

based. For the ordered-tree embedding, our algorithm needs only O(|T|⋅|P|) time and O(|T|⋅|P|) space, where

|T| and |P| stands for the numbers of the nodes in the target tree T and the pattern tree P, respectively. For the

unordered-tree embedding, we give an algorithm that needs O(|T|⋅|P|⋅2

) time, where k is the largest out-

degree of any node in P.

1 INTRODUCTION

In XML (World Wide Web Consortium, 1998)

(World Wide Web Consortium, 1998b), data is

represented as a tree; associated with each node of

the tree is an element type from a finite alphabet ∑.

The children of a node are ordered from left to right,

and represent the content (i.e., list of subelements) of

that element. XML queries such as XPath (w3.org,

http), XQuery (Robie et al., 1998), XML-QL

(Deutsch et al., 1989) (Florescu et al., 1999) and

Quilt (Chamberlinet al., 2000) use tree patterns to

extract relevant portions from the input database. A

tree pattern query (or called a query tree) that we

consider in this paper, denoted by TPQ from now

on, is defined as follows. The nodes of a tree are

labeled by element types from ∑ ∪ {*}, where * is a

wild card, matching any element type. The type for a

node v is denoted τ(v). There are two kinds of edges:

child edges (c-edges) and descendant edges (d-

edges). A c-edges from node v to node u is denoted

by v → u in the text, and represented by a single arc;

u is called a c-child of v. A d-edge is denoted v ⇒ u

in the text, and represented by a double arc; u is

called a d-child of v.

In any DAG (directed acycli

c graph), a node u is

said to be a descendant of a node v if there exists a

path (sequence of edges) from v to u. In the case of a

TPQ, this path could consist of any sequence of c-

edges and/or d-edges.

An embedding of a TPQ P in

to an XML document T

is a mapping f: P → T, from the nodes of P to the

nodes of T, which satisfies the following conditions

(Ramanan 2002):

1. Preserve node type: For each v ∈ P, v and f(v)

are

of the same type.

2. Preserve c/d-ch

ild relationships: If v → u in P,

then f(u) is a child of f(v) in T; if v ⇒ u in P,

then f(u) is a descendant of f(v) in T.

Any document T, in which P can be embedded, is

said to contain P and considered to be an answer.

To handle all the possible XPath queries, we allow a

de u in a TPQ P to be associated with a set of

predicates. We distinguish among three different

kinds of predicates: current node related predicates

(called current-predicates), child node related

predicates (called c-predicates), and descendant

related predicates (called d-predicates). A current-

predicate p is just a built-in predicate applied to the

current node; i.e., a node v in T, which matches u,

must satisfy this predicate associated with u. A c-

predicate is a built-in predicate applied to the

children of the current node. That is, for each node v

in T, which matches u, each of its children (or one of

its children) must satisfy this predicate. Similarly, a

d-predicate must be satisfied by all the descendants

of the node (or one of its descendants), which

matches u. Without loss of generality, we assume

that associated with u is a conjunctive-disjunctive

normal form: (p

∨ ... ∨ ) ∧ ... ∧ (p

11i

∨ ...

∨ ), where each p

kki

is a predicate.

For example, the following XPath query:

chapter[section[//paragraph[text() contains

‘informatics’]/following-sibling::*][position() =

3]]/*[self::section or self::chapter-notes]

can be represented by a tree shown in Fig. 1.

In the query tree shown in Fig. 1, each node is

abeled with a type or *, and may or may not be

Chen Y. (2006).

ON THE EVALUATION OF TREE PATTERN QUERIES.

In Proceedings of the First International Conference on Software and Data Technologies, pages 79-85

DOI: 10.5220/0001308700790085

 SciTePress

associated with a conjunctive-disjunctive normal

form of predicates, which are used to describe the

conditions that the node (and/or its children) has to

satisfy, or the relationships of the node with some

other nodes:

Figure 1: A sample TPQ.

- τ(u

) = chapter. It matches any node v in T if it is

associated with type ‘chapter’.

- τ(u

) = section; and associated with a current

predicate position() = 3. It matches any node v in T

if it is a third child of its parent and associated with

type ‘section’.

- τ(u

) = *; and associated with a disjunction of

current-predicates: τ(u

) = section or τ(u

) = chapter-

notes. It matches a node v in T if it is associated with

type ‘section’ or ‘chapter-notes’.

- τ(u

) = paragraph; associated with a c-predicate:

text() contains ‘informatics’. It matches a node v in

T if it is associated with type ‘paragraph’ and has a

text child that contains word ‘informatics’.

- τ(u

) = *; associated with a current-predicate:

following-sibling(v

), which indicates that if u

match a node in T, that node must directly follows

any node that matches u

, i.e., any node with type

‘paragraph’ and having a text child node that

contains word ‘informatics’.

Accordingly, the embedding f of a TPQ P into a

document T is modified as follows.

1. For each v ∈ P, v and f(v) are of the same type;

and f(v) satisfies all the current-predicates

associated with v.

2. If v → u in P, then f(u) is a child of f(v) in T;

and f(u) satisfies all the c-predicates associated

with v. If v ⇒ u in P, then f(u) is a descendant of

f(v) in T; and f(u) satisfies all the d-predicates

associated with v.

In this paper, we mainly discuss how such a tree

embedding can be efficiently checked.

The rest of the paper is organized as follows. In

Section 2, we review some related work. In Section

3, we discuss a new strategy for evaluating XPath

queries by handling them as ordered tree embedding

problems. In Section 4, another strategy is proposed

based on unordered tree embedding. Finally, a short

conclusion is set forth in Section 5.

2 RELATED WORK

Recently, much research has been conducted on the

evaluation of such XML queries (Gottlob et al.,

2005) (Gottlob et al., 2005) (Wang et al., 2003)

(Wang et al., 2005) (Zhang et al., 2001). Here, we

just mention some of them, which are very closely

related to the work to be discussed. The first one is

based on Inversion on elements and words (Zhang et

al., 2001), which needs O(n

) time in the worst case

where n and m are the number of the nodes in T and

P, respectively. The second is based on Inversion on

paths and words (w3.org, http), which improves the

first one by introducing indexes on paths. The time

complexity of this method is still exponential and

needs O((n⋅h)

) time in the worst case, where h is the

average height of a document tree and k is the

number of joins conducted. The main idea of the

third method is to transform a tree embedding into a

string matching problem (Knuth, 1969) (Ramanan

2002). The time complexity is O(n⋅m⋅h). This

polynomial time complexity is achieved by

imposing an ordering on the siblings in a query tree.

That is, the method assumes that the order of

siblings is significant. If the query tree is ordered

differently from the documents, a tree embedding

may not be found even though it exists. In this case,

the query tree should be reordered and evaluated

once again. Another problem of (Wang et al., 2003)

is that the results may be incorrect. That is, a

document tree that does not contain the query tree

may be designated as one of the answers due the

ambiguity caused by identical sibling nodes. This

problem is removed by the so-called forward prefix

checking discussed in (Wang et al., 2005). Doing so,

however, the theoretical time complexity is

dramatically degraded to O(n

⋅m⋅h). The last one is

to represent an XPath query as a parse tree and

evaluate such a parse tree bottom-up or top-down

(Gottlob et al., 2005). In (Gottlob et al., 2005), it is

claimed that the bottom-up strategy needs only

O(n

⋅m

) time and O(n

⋅m

) space, so does its top-

down algorithm. But in another paper (Gottlob et al.,

2005) of the same authors, the same problem is

claimed to be NP-complete. It seems to be

controversial. In fact, the analysis made in (Gottlob

et al., 2005) assumes that the query tree is ordered

while by the analysis conducted in (Gottlob et al.,

2005) the query tree is considered to be unordered,

leading to different analysis results.

τ(u

) = section or

τ(u

) = chapter-notes

paragraph

text() contains

‘informatics’

chapte

section

position() = 3

following-sibling(u

)

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

In this paper, we first present an algorithm based on

the ordered tree embedding. Its time complexity is

bounded by O(n⋅m). Then, another strategy based on

the unordered tree embedding is discussed, which

needs O n⋅m⋅2

) time time, where k is the largest

out-degree of any node in P.

3 A STRATEGY BASED ON

ORDERED-TREE EMBEDDING

In this section, we mainly discuss a strategy for the

query evaluation based on ordered-tree embedding,

by which the order between siblings is significant.

The query evaluation based on unordered-tree

embedding is discussed in the next section.

In general, a tree pattern query P can be considered

as a labeled tree if we extend the meaning of label

matching by including the predicate checking. That

is, to check whether a node v in a document T

matches a node u in P, we not only compare their

types, but also check whether all the predicates

associated with u can be satisfied. Such an

abstraction enables us to focus on the hard part of

the problem.

In the following, we first give the basic definitions over

ordered- tree embedding in 2.1. Then, we propose an

algorithm for solving this problem in 2.2.

3.1 Basic Concepts

Technically, it is convenient to consider a slight

generalization of trees, namely forests. A forest is a

finite ordered sequence of disjoint finite trees. A tree

T consists of a specially designated node root(T)

called the root of the tree, and a forest <T

, ..., T

where k ≥ 0. The trees T

, ..., T

are the subtrees of

the root of T or the immediate subtrees of tree T, and

k is the out-degree of the root of T. A tree with the

root t and the subtrees T

, ..., T

is denoted by <t; T

..., T

>. The roots of the trees T

, ..., T

are the

children of t and siblings of each other. Also, we call

, ..., T

the sibling trees of each other. In addition,

, ..., T

i-1

are called the left sibling trees of T

, and

i-1

the direct left sibling tree of T

. The root is an

ancestor of all the nodes in its subtrees, and the

nodes in the subtrees are descendants of the root.

The set of descendants of a node v (excluding v) is

denoted by desc(v). A leaf is a node with an empty

set of descendants. The children of a node v is

denoted by chidren(v).

Sometimes we treat a tree T as the forest <T>. We

also denote the set of nodes in a forest F by V(F).

For example, if we speak of functions from a forest

F to a forest G, we mean functions mapping V(F)

onto V(G). The size of a forest F, denoted by |F|, is

the number of the nodes in F. The restriction of a

forest F to a node v with its descendants is called a

subtree of F rooted at v, denoted by F[v].

Let F = <T

, ..., T

> be a forest. The preorder of a

forest F is the order of the nodes visited during a

preorder traversal. A preorder traversal of a forest

, ..., T

> is as follows. Traverse the trees T

, ..., T

in ascending order of the indices in preorder. To

traverse a tree in preorder, first visit the root and

then traverse the forest of its subtrees in preorder.

The postorder is defined similarly, except that in a

postorder traversal the root is visited after traversing

the forest of its subtrees in postorder. We denote the

preorder and postorder numbers of a node v by

pre(v) and post(v), respectively.

Using preorder and postorder numbers, the

ancestorship can be checked as follows.

Lemma 1. Let v and u be nodes in a forest F. Then,

v is an ancestor of u if and only if pre(v) < pre(u)

and post(u) < post(v).

Proof. See Exercise 2.3.2-2 in (Knuth, 1969).

Similarly, we check the left-to-right ordering as

follows.

Lemma 2. Let v and u be nodes in a forest F. Then,

v appears on the left side of u if and only if pre(v) <

pre(u) and post(v) < post(u).

Proof. The proof is trivial.

Now we give the definition of ordered tree

embeddings. In this definition, we simply use ‘label

matching’ to refer to both type matching and

predicate checking.

Definition 1. Let P and T be rooted labeled trees.

We define an ordered embedding (f, P, T) as an

injective mapping f: V(P) → V(T) such that for all

nodes v, u ∈ V(P),

i) label(v) = label(f(v)); (label preservation

condition)

ii) if (v, u) is a c-edge, then f(v) is the parent of f(u);

(child condition)

iii) if (v, u) is a d-edge, then f(v) is an ancestor of

f(u); (ancestor condition)

iv) v is to the left of u iff f(v) is to the left of f(u).

(sibling condition)

As an example, we show an ordered tree embedding

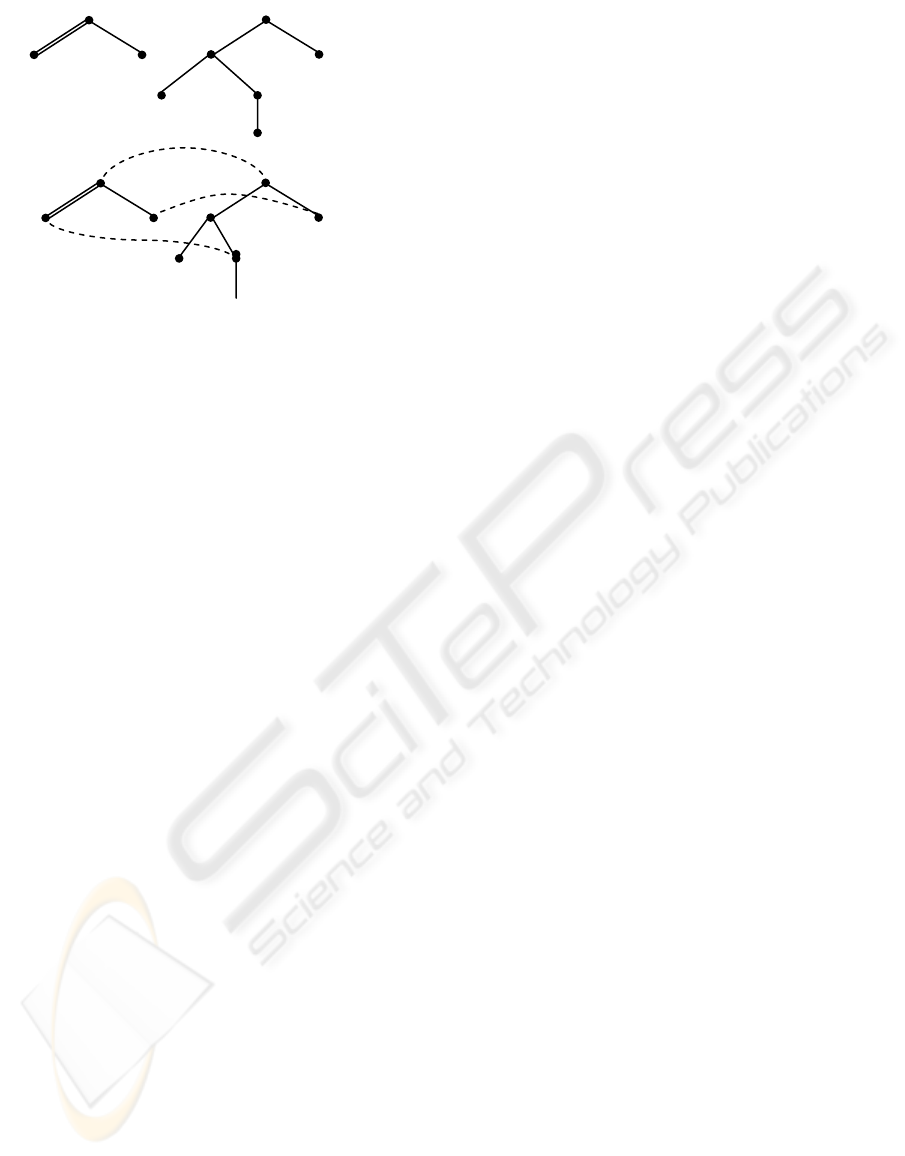
in Fig. 2.

In Fig. 2(a), the tree on the left can be embedded in

the tree on the right because a mapping as shown in

Fig. 2(b) can be recognized, which satisfies all the

conditions specified in Definition 1. In addition, Fig.

2(b) shows a special kind of tree embeddings, which

is very critic to the design of our algorithm and also

quite useful to explain the main idea of our design.

ON THE EVALUATION OF TREE PATTERN QUERIES

Figure 2: An example of ordered tree embedding.

Definition 2. Let P and T be trees. A root-

preserving embedding of P in T is an embedding f of

P in T such that f(root(P)) = root(T). If there is a

root-preserving embedding of P in T, we say that the

root of T is an occurrence of P.

For example, the tree embedding shown in Fig. 2(b)

is a root preserving embedding. Obviously,

restricting to root-preserving embedding does not

lose generality.

Finally, we use Lemma 2 to define an ordering of

the nodes of a forest F given by v v’ iff post(v) <

post(v’) and pre(v) < pre(v’). Also, v v’ iff v v’ or v

= v’. The left relatives, lr(v), of a node v ∈ V(F) is

the set of nodes that are to the left of v (i.e., all those

nodes that precede v both in preorder and postorder),

and similarly the right relatives, rr(v), is the set of

nodes that are to the right of v (i.e., all those nodes

that follow v both in preorder and postorder).

Throughout the rest of the paper, we refer to the

labeled trees simply as trees since we do not discuss

unlabeled trees at all.

3.2 Algorithm Description

The algorithm to be given is in fact a dynamic

programming solution. During the process, two m

n (m = |P|, n = |T|) matrices are maintained and

computed to discover tree embeddings. They are

described as follows.

1. The nodes in both P and T are numbered in

postorder, and the nodes are then referred to by their

postorder numbers.

2. The first matrix is used to record subtree

embeddings, in which each entry c

(i ∈ {1, ..., m}, j

∈ {1, ..., n}) has value 0 or 1. If c

= 1, it indicates

that there is a root preserving embedding of the

subtree rooted at the node indexed by i (in P) in the

subtree rooted at the node indexed by j (in T).

Otherwise, c

= 0. This matrix is denoted by c(P, T).

3. In the second matrix, each entry d

(i ∈ {1, ..., m},

j ∈ {0, ..., n - 1}) is defined as follows:

= min({x ∈ rr(j) | c

= 1} ∪ {α}),

where α = n + 1. That is, d

contains the closest right

relative x of node j such that T[x] contains P[i], or n

+ 1, indicating that there exists no right relative x of

node j such that P[i] can be root-preservingly

embedded in T[x]. This matrix is denoted by d(P, T).

In the above definitions of matrices, we should

notice that the indexes of d(P, T) is slightly different

from those of c(P, T). That is, for d(P, T), j ∈ {0, ...,

n - 1} (instead of {1, ..., n}), and j = 0 is considered

to be a virtual node left to any node in T.

The matrix c(P, T) is established by running the

following algorithm, called ordered-tree-embedding

while d(P, T) is employed to facilitate the

computation. Initially, c

= 0, and d

= 0 for all i and

j. In addition, each node v in T is associated with a

quadruple (α(v), β(v), χ(v), δ(v)), where α(v) is v’s

preorder number, β(v) is v’s postorder number, χ(v)

is v’s level number, and δ(v) = min(desc(v)). By the

level number of v, we mean the number of ancestors

of v, excluding v itself. For example, the root of T

has the level number 0, its children have the level

number 1, and so on. Obviously, for two nodes v

and v

, associated respectively with (α

, β

, χ

, δ

)

and (α

, β

, χ

, δ

), if χ

= χ

+ 1, α

< α

and β

, we have v

∈ children(v

In the following algorithm, we assume that for T

there exists a virtual node with postorder number 0,

which is left to any node in T.

Algorithm ordered-tree-embedding(T, P)

Input: tree T (with nodes 0, 1, ..., n) and tree P (with nodes

1, ..., m)

Output: c(P, T), which shows the tree embedding.

begin

1. for u := 1, ..., m do

2. { for v := 0, ..., n - 1 do {d

:= n + 1;}

3. l := 0;

4. for v := 1, ..., n do

5. {if label(u) = label(v) then

6. let u

, ..., u

be the children of u;

7. j := δ(v) - 1;

8. i := 1;

9. while i

≤

k and j < v do

10. {j := ;

11. if (u, u

) is a d-edge then

12. {if j ∈ desc(v) then i := i + 1;

13. else /*(u, u

) is a c-edge.*/

14. {if j ∈ children(v) and j is a c-child

then i := i + 1;}

15. }}

16. if j = k then

17. {c

:= 1;

18. while l ∈ lr(v) do {d

; = v; l := l + 1;}

(a)

(b)

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

19. }

20.}

end

To know how the above algorithm works, we should

first notice that both T and P are postorder-

numbered. Therefore, the algorithm proceeds in a

bottom-up way (see line 1 and 4). For any node u in

P and any node v in T, if label(u) = label(v), the

children of u will be checked one by one against

some nodes in desc(v). The children of u is indexed

by i (see line 6); and the nodes in desc(v) is indexed

by j (see line 10). Assume that the nodes in desc(v),

which are checked during the execution of the

while-loop (see lines 9 - 15), are j

, ..., j

. Then,

each j

(1 ≤ g

≤

h) satisfies the following conditions

(see line 11):

(i) δ(v) - 1 < j

< v (i.e., j

∈ desc(v)),

(ii) j

= with j

= δ(v) - 1.

Therefore, for any j

and j

∈ {j

, ..., j

}, they must

be on different paths according to the definition of

d(P, T). In addition, in the while-loop, if (u, u

) is a

d-edge, the algorithm checks whether j ∈ desc(v)

(see line 12). If it is the case, u

has a matching

counterpart in desc(v) and i will be increased by 1.

Thus, in a next step, the algorithm will check the

direct right sibling of u

against a node that is one of

the right reletives of j. If (u, u

) is a c-edge, we will

check whether j ∈ children(v) (see line 14). In line

16, we will check whether i = k. If it is the case, we

have desc(v) contains all subtrees P[u

], ..., P[u

])

This indicates that we will have a root-preserving

embedding of P[u] in T[v]. Therefore, c

is set to 1

(see line 17). Also, for any node l that is one of the

left relatives of v, d

is set to 1 (see line 18). It is

because v must be the closest right relative of any of

such nodes in T such that the subtree rooted at it (i.e,

T[v]) root-preservingly contains P[u].

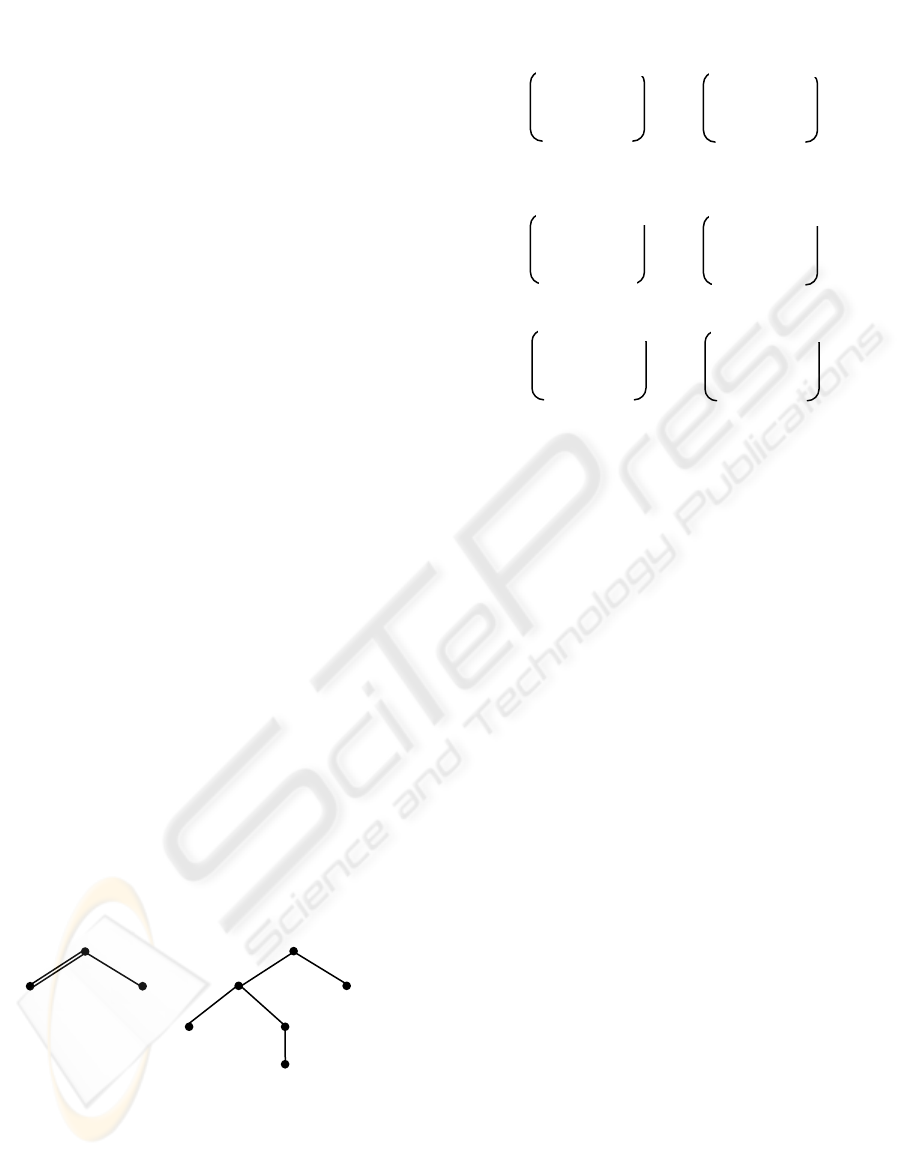
Example 1. As an example, consider the trees

shown in Fig. 3. The nodes in them are postorder

numbered.

Figure 3: Labeled trees and postorder numbering.

When we apply the algorithm to these two trees, c(P,

T) and d(P, T) will be created and changed in the

way as illustrated in Fig. 4, in which each step

corresponds to an execution of the outmost for-loop.

Figure 4: A sample trace.

In step 1, we show the values in c(P, T) and d(P, T)

after node 1 in P is checked against every node in T.

Since node 1 in P matches node 2, 3 and 5 in T, c

, and c

are all set to 1. Furthermore, d

is set to

2 since the closest right relative of node 0 in T,

which matches node 1 in P, is node 2 in T. The same

analysis applies to d

. Since the closest right

relative of node 2, 3, 4 in T, which matches node 1

in P, is node 5 in T, d

, d

, and d

are all set to 5.

Finally, we notice that d

is equal to 7, which

indicates that there exists no right relative of node 5

that matches node 1 in P.

In step 2, the algorithm generates the matrix entries

for node 2 in P, which is done in the same way as

for node 1 in P.

In step 3, node 3 in P will be checked against every

node in T, but matches only node 6 in T. Since it is

an internal node (in fact, it is the root of P), its

children will be further checked. First, to check its

first child, the algorithm will examine d

, which is

equal to 2, showing that node 2 in T is the closest

right relative of node 0 that matches node 1 in P. In

a next step, the algorithm will check the second

child of node 3 in P. To do this, d

is checked. d

’s

value is 5, showing that the closest relative of node 2

in T, which matches node 2 in P, is node 5 in T. In

addition, since the edge (3, 2) in P is a c-edge, the

algorithm will check whether node 5 in T is a child

of node 6. Since it is the case, we have a root-

preserving embedding of P[3] in T[6]. Finally, we

notice that when the second child of node 3 in P is

checked, the algorithm begins the checking from d

rather than d

. In this way, a lot of useless

checkings is avoided.

1 3

2 1

step 1:

d(P, T)

)

0 1 1 0 1 0

0 0 0 0 0 0

000000

1 2 3 4 5 6

2 2 5 5 5 7

0 0 0 0 0 0

1 2 3 4 5 6

step 2:

c(P, T)

d(P, T)

0 1 1 0 1 0

000000

1 2 3 4 5 6

2 2 5 5 5 7

0 0 0 0 0 0

1 2 3 4 5 6

d(P, T)

step 3:

c(P, T)

0 1 1 0 1 0

000001

1 2 3 4 5 6

2 2 5 5 5 7

6 7 7 7 7 7

1 2 3 4 5 6

ON THE EVALUATION OF TREE PATTERN QUERIES

Proposition 1. Algorithm ordered-tree-embedding(

T, P) computes the values in c(P, T) and d(P, T)

correctly.

Proof. We prove the proposition by induction on the

sum of the heights of T and P, h. Without loss of

generality, assume that height(T) ≥ 1 and height(P)

≥ 1.

Basic step. When h = 2, the proposition trivially

holds.

Induction hypothesis. Assume that when h = l, the

proposition holds.

Consider T = <t; T

, ..., T

> and P = <p; P

, ..., P

with height(T) + height(P) = l + 1. Obviously, we

have height(T

) + height(P) ≤ l and height(T) +

height(P

) ≤ l. Therefore, in terms of the induction

hypothesis, the algorithm computes the values in

c(P, T

) and d(P, T

), as well as the values in c(P

, T)

and d(P

, T) correctly (i = 1, ..., k; j = 1, ..., q).

Assume that V(P) = {1, ..., m} and V(T) = {1, ..., n}.

Then, the values for c

(i = 1, ..., m - 1; j = 1, ..., n -

1) and d

(i = 1, ..., m - 1; j = 0, ..., n - 2) are all

correctly generated. Now we will check c

and d

n-1

(i = 1, ..., m), as well as c

(j = 1, ..., n) and d

(j =

0, ..., n - 1) to see whether they can be correctly

produced. Let i

, ..., i

be the children of i. If label(i)

= label(n), for each i

(1 ≤ f

≤

s), some ’s will be

checked. Obviously, i

< i and j < n. According to the

induction hypothesis, all such ’s are correctly

generated. Depending on whether (i, i

) is a d-edge

or c-edge, the algorithm will check whether j ∈

desc(n) or j ∈ children(n). In addition, any two

nodes j

and j

, which are checked against two

different children of i, are not on the same path.

Therefore, c

(i = 1, ..., m) is correctly created, so is

,n-1 (i = 1, ..., m). A similar analysis applies to c

(j = 1, ..., n) and d

(j = 0, ..., n - 1).

Proposition 2. Algorithm ordered-tree-embedding

(T, P) requires O(|T|⋅|P|) time and space.

Proof. During the execution of the outermost for-

loop, l may increases from 0 to n. Therefore, the

time spent on the execution of line 18 in the whole

process is bounded by O(n). An execution of the

while-loop from line 9 to 15 needs O(d

) time,

where d

represents the outdegree of node u in P. So

the total time is bounded by

O(n) + O( ) = O(n) + O( )

∑∑

= O(n) + O( ) = O(n⋅m).

∑

Obviously, to maintain c(Q) and d(Q), we need

O(n

) space.

4 A STRATEGY BASED ON

UNORDERED TREE

EMBEDDING

Now we turn to the unordered version of the

problem, which appears to be essentially more

difficult. A tree P is an unordered included tree of a

tree T if the nodes of P can be injectively mapped

onto the nodes of T preserving the labels and the

ancestorship relation between nodes. Such a

mapping is called an unordered embedding. We do

not require the left-to-right order of the nodes to be

preserved in an unordered embedding. But sibling

nodes should not be mapped to those nodes that are

on the same path.

To facilitate the algorithm description, we will use

some concepts from the hypergraph theory (Berge,

1989).

Definition 3. Let U = {u

, …, u

} be a finite set of

nodes. A hypergraph on U is a family H = {E

, …,

} of subsets of U such that

(1) E

≠

(i = 1, 2, …, l)

(2) = U.

∪

A simple hypergraph (or Sperner family) is a

hypergraph H = {E

, …, E

} such that

(3) E

⊂ E

⇒ i = j.

As for a graph H, the order of H, denoted by n(H), is

the number of nodes. The number of edges will be

denoted by m(H) and the rank(H) is defined to be

r(H) =

Emax . It can be proved that m(H) ≤

(Berge, 1989).

⎣⎦

⎜

⎝

⎛

⎟

⎠

⎞

2/n

Let A ⊂ U be a subset. We call the family

= {E

∩ A | 1 ≤ i ≤ l, E

∩ A E

≠

}

the sub-hypergraph induced by A.

Definition 4. Let H = {E

, …, E

} be a hypergraph

on U and H’ = {F

, …, H

l’

} be another hypergraph

on V. The product of H and H’, denoted as H × H’,

is a hypergraph, whose nodes are the elements of the

Cartesian product U × V, and whose edges are the

sets E

× F

with 1 ≤ i ≤ l and 1 ≤ j ≤ l’. Obviously,

n(H × H’) = n(H)n(H’) and m(H × H’) =m(H)m(H’).

However, if U = V, we have n(H × H’) = n(H) and

m(H × H’) ≤ .

⎣⎦

⎜

⎝

⎛

⎟

⎠

⎞

2/n

As with the ordered tree embedding, we will

maintain two matrices Q(P, T) and S(P, T) to control

the computation.

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

1. In Q(P, T), an entry q

is 1 if the subtree rooted

at j in T includes the subtree rooted at i in P.

Otherwise, it is 0.

2. In S(P, T), each entry s

is defined as follows.

Let i

, i

, …, i

be the child nodes of i. s

is a

hypergraph H

= {E

, …, E

}over {i

, i

, …, i

}

such that T[j], the subtree rooted at j, includes

each E

(g = 1, …, l}, that is, for each E

, the

subtree rooted at j includes all the subtrees

rooted at the nodes in E

. But T[j] cannot

include E

∪ E

for any i, j ∈{1, …, l }.

Algorithm unordered-embedding(T, P)

Input: tree T (with nodes 1, ..., n) and tree P (with nodes 1,

..., m)

Output: Q(P, T), which shows the tree embedding.

begin

1. for v := 1, ..., n do

2. {for u := 1, ..., m do

3. {if q

:= 0 then

4. {let v

, …, v

be the child nodes of v;

5. H := × … × ;

6. let u

, …, u

be the child nodes of u;

7. if {u

, …, u

} ∈ H then set q

to 1;

8. else s

:= H;

9. }

10. }

11. let u

, …, u

be nodes covered by v;

12. for each ancestor v’ of v, := 1 for i = 1, …, l;

'vu

13. construct hypergraph H

= {{u

}, …, {u

}};

14. for u := 1, ..., m do

15. {let A be the set of u’s child nodes;

16. s

:= H

;

17. }

20. }

End

The execution of line 5 will dominate the running

time of the algorithm. Let k be the largest out-degree

of any node in P. Then, the size of each s

bounded by ≤ 2

⎣⎦

⎜

⎝

⎛

⎟

⎠

⎞

. Especially, the size of

any product hypergraph of the form s

× s

uv’

bounded by 2

(and so is s

× s

uv’

× s

uv’‘

, …, and so

on.) So the time complexity of the algorithm is on

the order of O(|T|⋅|P|⋅2

4 CONCLUSION

In this paper, a new strategy for evaluating XPath

queries is discussed. The main idea of the strategy is

to handle an XPath query as tree embedding

problem. Two strategies are proposed. One is or-

dered tree embedding based, and the other is

unordered tree embedding based. For the ordered

tree embedding problem, our algorithm needs only

O(|T|⋅|P|) time and O(|T|⋅|P|) space, where |T| and |P|

stands for the numbers of the nodes in the target tree

T and the pattern tree P, respectively. For the

unordered-tree embedding, we give an algorithm

that needs O(|T|⋅|P|⋅2

) time, where k is the largest

out-degree of any node in P.

REFERENCES

C. Berge, Hypergraphs, Elsevier Science Publisher,

Amsterdam, 1989.

D.D. Chamberlin, J. Robie and D. Florescu, Quilt: An

XML Query Language for Heterogeneous Data

Sources, WebDB 2000.

A. Deutsch, M. Fernadez, D. Florescu, A Levy, and D.

Suciu, XML-QL: A Query Language for XML,

Technical report, World Wide Web Consortium, 1989,

http://www.w3.org/TR/Note-xml-ql.

D. Florescu and D. Kossman, Storing and Querying XML

Data using an RDBMS. IEEE Data Engineering

Bulletin, 22(3), 1999.

http://www.w3.org/TR/xpath.

D.E. Knuth, The Art of Computer Programming, Vol. 1,

Addison-Wesley, Reading, MA, 1969.

P. Ramanan, Efficient Algorithms for Minimizing Tree

Pattern Queries, ACM SIGMOD 2002, June 2002,

Madison, Wisconsin, USA.

J. Robie, J. Lapp, and D. Schach, XML Query Language

(XQL), 1998. http://www.w3.org/TandS/

QL/QL98/pp/ xql.html.

World Wide Web Consortium, Extensible Markup

Language (XML) 1.0. http//www.w3.org/TR/1998/

REC-xml/ 19980210, Febuary 1998.

World Wide Web Consortium, Extensible Style Language

(XML) Working Draft, Dec. 1998.

http//www.w3.org/TR/ 1998/WD-xsl-19981216.

G. Gottlob, C. Koch, and R. Pichler, Efficient Algorithms

for Processing XPath Queries, ACM Transaction on

Database Systems, Vol. 30, No. 2, June 2005, pp. 444-

491.

G. Gottlob, C. Koch, and K.U. Schulz, Conjunctive

Queries over Trees, in Proc. PODS 2004, June 2004,

Paris, France, pp. 189-200.

H. Wang, S. Park, W. Fan, and P.S. Yu, ViST: A Dynamic

Index Method for Querying XML Data by Tree

Structures, SIGMOD Int. Conf. on Management of

Data, San Diego, CA., June 2003.

H. Wang and X. Meng, On the Sequencing of Tree

Structures for XML Indexing, in Proc. Conf. Data

Engineering, Tokyo, Japan, April, 2005, pp. 372-385.

C. Zhang, J. Naughton, D. DeWitt, Q. Luo and G.

Lohman, “On Supporting Containment Queries in

Relational Database Management Systems, in Proc. of

ACM SIGMOD Intl. Conf. on Management of Data,

California, USA, 2001.

ON THE EVALUATION OF TREE PATTERN QUERIES