
A PRIMITIVE EXECUTION MODEL
FOR HETEROGENEOUS MODELING
Frédéric Boulanger
Supélec – Département Informatique
3 rue Joliot-Curie, 91192 Gif-sur-Yvette cedex, France
Guy Vidal-Naquet
Supélec and Université Paris-Sud
3 rue Joliot-Curie, 91192 Gif-sur-Yvette cedex, France
Keywords:
Heterogeneous modeling, Models of computation, Execution models.
Abstract:
Heterogeneous modeling is modeling using several modeling methods. Since many different modeling meth-
ods are used in different crafts, heterogeneous modeling is necessary to build a heterogeneous model of a
system that takes the modeling habits of the designers into account.
A model of computation is a formal description of the behavioral aspect of a modeling method. It is the
set of rules that allows to compute the behavior of a system by composing the behaviors of its components.
Heterogeneous modeling allows parts of the system to obey some rules while other parts obey other rules for
the composition of their behaviors.
Computing the behavior of a system which is modeled using several models of computation can be difficult
if the meaning of each model of computation, and what happens at their boundary, is not well defined. We
propose an execution model that provides a framework of primitive operations that allow to express how a
model of computation is interpreted in order to compute the behavior of a model of a system. When models
of computation are “implemented” in this execution model, it becomes possible to specify exactly what is the
meaning of the joint use of several models of computation in the model of a system.
1 CONTEXT
The design of most complex systems appeals to dif-
ferent crafts that are organized around sets of specific
design methods, e.g. for industrial control or signal
processing. These methods are adapted to specific as-
pects of a craft, and designers have a correct intuition
of their semantics.
When integrating the different parts of a system, we
generally translate the model of each part into a com-
mon low level formalism, or even into a common im-
plementation language. By doing so, we loose all the
information that tells how we went from the specifi-
cation of the subsystem to its model. Therefore, when
building the whole system, we cannot take advantage
of the different choices of realization offered by the
model, since they have been “frozen” in the low level
implementation.
Another issue is that, when validating the behavior
of the whole system, it will be difficult to find what
should be changed in the model of a subsystem to
insure a global property , since the low level imple-
mentation does not carry enough information about
the design of the subsystem.
Heterogeneous modeling tries to overcome these
issues by allowing to describe the whole system as a
composition of subsystems that are designed accord-
ing to different methods (Liu et al., 2003).
It does not provide a greater expressive power than
other modeling techniques, but it allows the different
teams that work on the design of a system to share a
common model of the system, while using their own
modeling techniques.
In the following, we present the actor paradigm
for heterogeneous modeling and we propose a con-
structive method for computing the behavior of het-
erogeneous models. Projects like KerMeta (Fleurey
et al., 2006) or Rosetta (Kong and Alexander, 2003)
are related to our works, but focus on different objec-
tives: KerMeta defines behaviors for the elements of
the Meta-Object Facility (MOF) of the OMG, while
Rosetta defines the combination of models of compu-
tation and uses a hierarchy of compatible models of
computation. Our objective is to provide a framework
in which any model of computation may be used to
compute the interactions of components of a system.
In this paper, we focus on the steps that are required
to compute the behavior of a model of a system.
247
Boulanger F. and Vidal-Naquet G. (2006).
A PRIMITIVE EXECUTION MODEL FOR HETEROGENEOUS MODELING.
In Proceedings of the First International Conference on Software and Data Technologies, pages 247-252
DOI: 10.5220/0001309502470252
Copyright
c
SciTePress
2 ACTORS, PORTS, RELATIONS
Our approach to modeling is based on the actor
paradigm: a system is built from components named
actors. Actors have properties and communicate
through ports. Ports have properties and are linked
by relations which also have properties. So, building
a model of a system amounts to using some actors, to
set their properties and the properties of their ports,
and to build relations between the ports of the actors.
The effective behavior of the model is obtained by in-
terpreting the properties and the relations according
to a model of computation.
Actors, ports, properties and relations are the ele-
ments of the abstract syntax of actor-oriented mod-
eling. Models of computation are semantics for this
abstract syntax: a model of computation is an inter-
pretation of the relations between the ports of actors
and the properties of these relations.
2.1 Roles of a Model of Computation
A model of computation allows to compute the ob-
servable behavior of a model of a system from the in-
dividual observable behaviors of its components. For
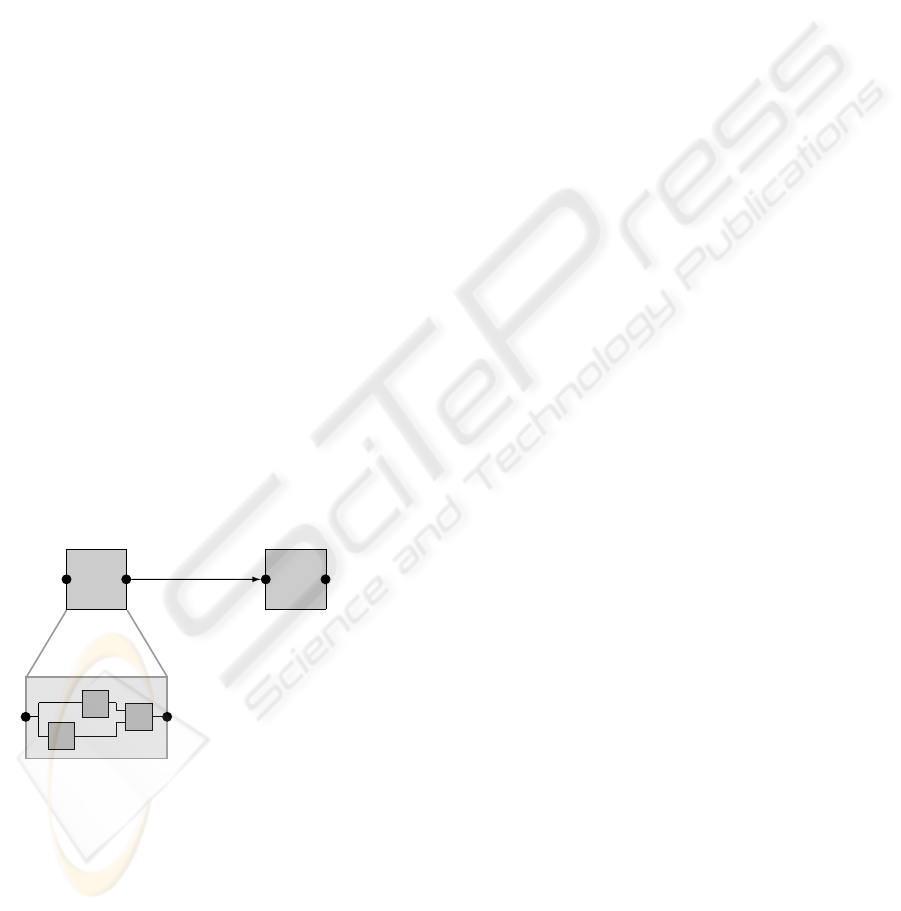
instance, on figure 1, the MoC
ext
model of compu-
tation computes the behavior of the top-level model
that contains actors A and B. This model of computa-
tion is in charge of computing the status (availability
of data and value) of B
in
from the status of A
out
. The
status of A
out
is determined from the status of A
in
by the behavior of A. In the example, this behavior is
described by a model that contains three actors and is
governed by the MoC
int
model of computation.
A
A
in
A
out
B
B
in
B
out
MoC
ext
MoC
int
Figure 1: Internal and external models of computation.
MoC
ext
is the “external model of computation” of
actor A. It is the model of computation that combines
its behavior with the behavior of other actors to com-
pute the behavior of a model. MoC
int
is the “internal
model of computation” of A. It is the model that com-
putes the behavior of A by combining the behaviors
of the actors of the model of A.
Information is obtained by observing the output
ports of actors, so the model of computation must tell
how information goes from output to input ports, and
when it is available on input ports. We can consider
the first aspect (the propagation of data from output
ports to input ports) as communication, and the sec-
ond aspect (when data is available) as control or syn-
chronization.
Communication consists generally in copying data
from output ports to input ports, but synchronization
can be more complex because it defines the type of
causality used by the model of computation. In some
models of computation, data produced on an output
port is available immediately on all input ports that
are in relation with that output port. In other mod-
els of computation, a notion of “tick” is used to relax
causality: a data sample produced on an output port is
available on all inputs ports that are in relation with it,
but only after the next tick. In other models of com-
putation, a notion of time is introduced to label data
samples with a time-stamp which tells when they are
available.
Communication and synchronization aspects must
be described precisely to define a model of computa-
tion. There are actually very few tools or languages
for describing these aspects. Most of the time, one
has to implement a model of computation in a generic
programming language.
3 EXECUTION MODEL
When the precise semantics of a model of compu-
tation is coded in a programming language, it is
generally done in the context of a framework like
Ptolemy II (Brooks et al., 2005) that provides sup-
port for the abstract syntax of the models. For such a
framework to support an open set of models of com-
putation, it must consider components as black boxes
that compute the availability and values of data on in-
put ports from the availability and values of data on
output ports.
We define here a generic execution model that can
be used with any model of computation. It relies on
models of computation for determining in which or-
der the actors of a model should be observed, and
how the values on input ports are computed from
the values observed on output ports. This execution
model has matured from previous works (Boulanger
et al., 2004; Feredj et al., 2004) based on the Ptolemy
framework.
3.1 The Nature of an Execution
Before defining our generic execution model, we must
define what is an execution of a model of a system.
In order to keep our approach generic, we ignore the
internal mechanisms of an actor, to focus on what and
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
248

when an actor produces data on its output ports, not
how it produces it.
Therefore, in the following, we will never “trigger”
the behavior of an actor, we will just observe its out-
put ports. The behavior of an actor can occur any time
– it can be a continuous process that runs during the
whole execution of the model – but it must provide a
coherent view each time its ports are observed. We
use a stroboscopic effect to observe the actors of a
model simultaneously in a series of snapshots. We
consider that an execution of a model is a sequence of
snapshots of the values available on the ports of the
model. In a given snapshot, each port has a single
defined value.
The nature of a snapshot depends on the model of
computation. The execution model only tells the ac-
tors that a snapshot is going to be taken, and then asks
them to approve the value of their ports as they appear
on the snapshot. For an analogy, a photographer tells
the actors “stay still”, and then ask them if they are
pleased by the picture.
This definition of an execution implies that we are
only interested in discrete behaviors. This is because
our goal is not to describe behaviors, but to compute
them. For instance, when we consider a model of a
physical system, like a system of ordinary differential
equations, we are not interested in finding properties
of these ODEs but in computing the value of the out-
puts of the system at a discrete set of instants.
Since we are interested in observations only, each
model of computation is insulated from the definition
of the others, and there is no need to define the com-
position of any pair of models of computation.
For instance, if an actor is a sensor which acquires
information from the external world, what is interest-
ing is the result of the measure, not the mechanism for
elaborating this measure.
3.2 Types of Actors
To define a generic execution model, we must con-
sider the different ways with which an actor produces
its outputs. Strict actors need to know the value of all
their inputs to determine the value of all their outputs
at once. With strict actors, a model cannot contain in-
stantaneous causality loops because a strict actor can-
not have an input that depends on the value of one
of its outputs in the same snapshot. Non-strict actors
can determine some of their outputs when they know
the value of only some of their inputs. A delay is a
non-strict actor: the value of its output depends only
on its state, which in turn depends on the value that its
input had in the previous snapshot. A logical OR gate
is also a non-strict actor because its output is known
as soon as one of its inputs is true.
When a model of computation supports non-strict
actors, the values of the ports are determined itera-
tively. First, actors are provided with known inputs
and they determine part of their outputs. These newly
determined outputs allow to compute new values for
inputs according to the model of computation. These
newly determined inputs allow actors to determine
more outputs, and so on until all the ports have a
known value. With such models of computation, it
is necessary to tell actors when new inputs become
available.
Actors, independently of their strict or non-strict
nature, may not agree with the value they have com-
puted for their outputs for the current snapshot. For
instance, consider a level-crossing detector. It pro-
duces an event when a signal crosses a threshold. If
the signal is computed by numerical integration of dif-
ferential equations, the integration step is adjusted so
that the value of the signal is computed with a given
precision. However, the measure may be refused if
the integration step is to large for the temporal preci-
sion required on the event, and the snapshot will be
computed again with a smaller integration step. A
snapshot is considered valid when all the actors of the
model agree with the value assigned to their ports.
3.3 Generic Execution Model
The taxonomy of actors presented above, and the fact
that we are only interested in observations of the ports
of actors, not in the activity of the actors, allows us to
define a generic execution model that is capable of ex-
ecuting models that obey any model of computation.
To attain such universality, we made as few assump-
tions about actors as possible, and we rely on an op-
erational description of the model of computation to
schedule observations and to compute the value and
availability of data on input ports from the data avail-
able on output ports.
One can wonder at the previous sentence since we
are used to outputs computed from inputs, not the re-
verse. The key is to consider that if actors produce
their outputs from their inputs, the model of compu-
tation interprets the relations between ports to deter-
mine what is available on inputs ports from what is
available on output ports.
We can now describe the steps of our execution
model to compute a snapshot of the execution of a
model of a system, and define the primitive operations
that an actor must provide:
1. the start_of_snapshot operation is invoked
on each actor of the model. In response to this in-
vocation, an actor prepares for the snapshot. For
instance, an actor that acquires information from
the environment of the system (reading data from
a file, sampling a sensor) should do it during this
step.
A PRIMITIVE EXECUTION MODEL FOR HETEROGENEOUS MODELING
249
2. the reset operation is invoked on each actor of
the model. In response to this invocation, an actor
resets its ports to the “unknown” state.
3. the update operation is invoked on the actors of
the model returned by the schedule operation of
the model of computation. In response to this invo-
cation, an actor makes data available on its output
ports. If the actor is strict, it makes data available
on all its output ports. If it is non-strict, it makes
data available only on the ports it can determine.
4. the operational description of the model of compu-
tation is used to compute the status (availability of
data and value of the data) of the input ports from
the status of the output ports.
5. if the model of computation determines that the
snapshot is complete, go to step 6, else, go back
to step 3. Steps 3 to 5 constitute an observation of
the model.
6. the validate_snapshot operation is invoked
on each actor of the model. In response to this
operation, an actor considers the data available on
its ports as definitive for this snapshot and tells
whether it considers it as correct or not. If it does
not validate the data, it should change some prop-
erty of the model of computation (e.g. the integra-
tion step in our example with the level-crossing de-
tector) so that a new computation of the snapshot
will compute data that it may validate.
7. if all the actors of the model have validated the
snapshot, go to step 8, else go back to step 2 to
compute the snapshot again with the new parame-
ters of the model of computation that have been set
by the actors which have not validated the snapshot.
8. when all the actors of the model have validated
the snapshot, the end_of_snapshot operation
is invoked on each actor of the model. This oper-
ation tells actors that the snapshot is valid and that
they can use the data available on their ports in their
own activity or to update their internal state if any.
Actors that provide data to the environment of the
system (writing data to a file, driving an actuator)
should do so during this step.
An actor should not update its internal state,
change its activity or perform any operation that may
have side effects on the environment between the
start_of_snapshot and end_of_snapshot
operations. The fact that a snapshot may be computed
several times to converge toward a result that is ac-
cepted by all the actors must not be visible outside the
model. For instance, if we consider our example of a
level-crossing detector, it may be necessary to com-
pute a snapshot several times before the integration
step becomes small enough, but outside the model,
only the last level-crossing event must be visible be-
cause it is the only one that has been considered as
correct. For the same reason, new data should not be
acquired during the computation of a valid snapshot.
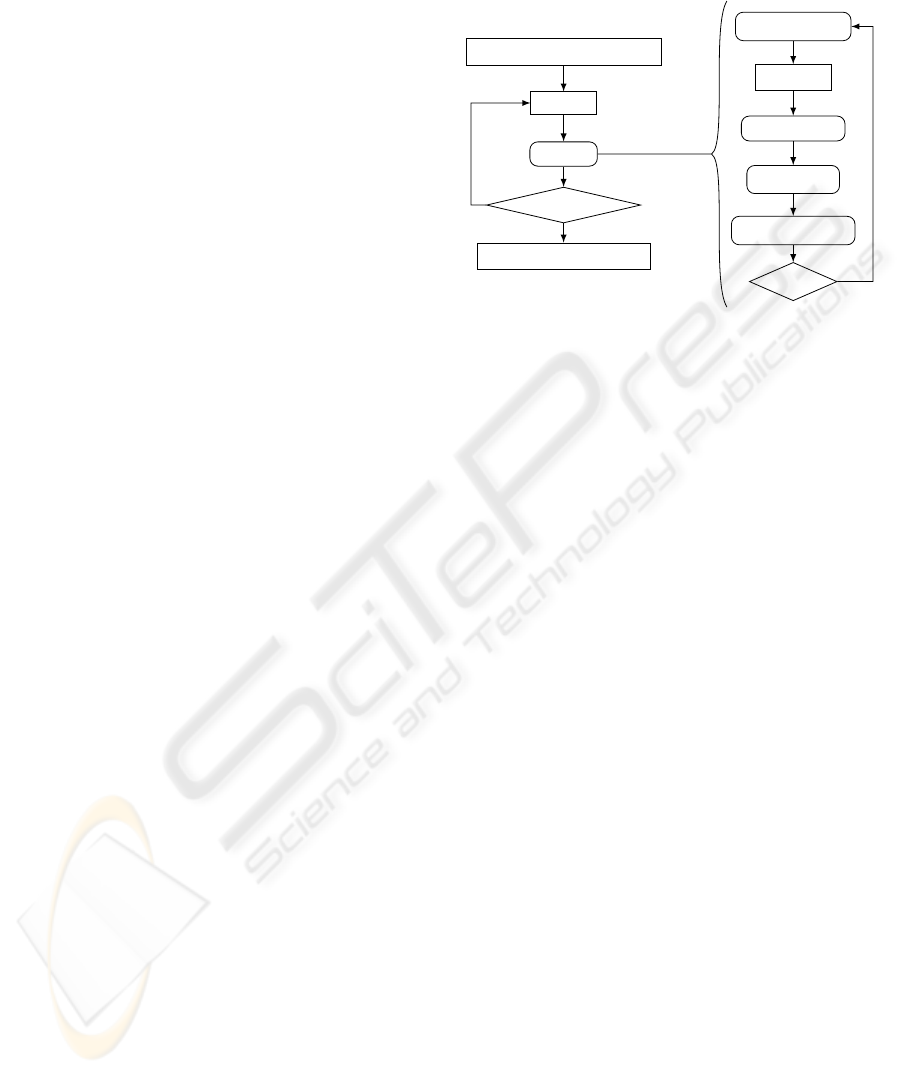
start_of_snapshot
reset
observe
validate?
end_of_snapshot
pre-schedule
update
in-schedule
propagate
post-schedule
done?
Figure 2: Steps of the generic execution model.
3.4 Discussion on Steps
The overall structure of our execution model is shown
on figure 2, with “actor operations” in rectangular
boxes, “model of computation operations” in rounded
corners boxes, and control choices in diamond shaped
boxes.
The schedule operations of the model of com-
putation determine which actors should be observed.
These operations are executed each time new data be-
comes available: at the beginning of an observation
(pre-schedule), in order to compute control from the
inputs of the model and to determine which actors
may produce observable outputs; after update (in-
schedule) in order to handle data made available on
the output ports of the actors; and at the end of the
observation (post-schedule), in order to handle the
outputs of the model.
Every model of computation must implement pre-
schedule because this operation tells which actors
will be observed in the current turn of the loop. The
other two schedule operations may do nothing in
models of computation where the control does not de-
pend on data.
The first and last steps of the computation of a
snapshot insulate the environment of the model from
the internal changes that occur in the model during
the computation of the observation of its ports. They
also insulate the behavior of the actors of a model
from the details of the computation of a snapshot of
this model, since an actor is not allowed to update its
internal state before the end_of_snapshot step.
For instance, an actor should not count the number of
times its reset, update or validate methods
are invoked and make its future behavior depend on
this count.
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
250

We can consider the start_of_snapshot
step as “sample the external world”, and the
end_of_snapshot as “update state, act on exter-
nal world”. Between these two steps, actors must
have a combinational behavior. This model is there-
fore very close to the synchronous sequential model
where registers are loaded on the ticks of a clock with
the results of combinational computations. In our ex-
ecution model, the clock is the series of instants at
which a snapshot exists. We do not need a more elab-
orate model of time at this level of the execution of a
model of a system.
The reset - validate loop is crucial for het-
erogeneous modeling because it is the way by which
the model of computation that is used for the internal
model of an actor can influence the model of com-
putation in which the actor is used. In a model of a
system, actors are just observed, and the observations
are combined by a model of computation to build an
observation of the model. However, the behavior of
each actor can also be described by a model of the ac-
tor (the actor is considered as a subsystem), and the
model of computation used to model the behavior of
the actor can be different from the first model of com-
putation. We call “external model of computation”
the model of computation that is used to combine the
behavior of an actor with the behavior of other ac-
tors, and “internal model of computation” the model
of computation that is used to describe the internal
behavior of an actor.
In order to avoid to compute all the possible combi-
nations of models of computation, we hide the inter-
nal model of computation to the eyes of the external
one. Since the external model of computation “de-
cides” when the ports of an actor are observed, the in-
ternal model of computation would have no control on
the computation of the snapshot if it could not refuse
a computation by making the actor return false to
the validate request.
The “observe” loop implements a well-
known technique to compute the behavior of
a model as a fixed-point. It is implemented
in Ptolemy II by the prefire, fire and
postfire methods. prefire is the equivalent
of start_of_snapshot in our execution model,
fire is equivalent to update and postfire to
end_of_snapshot. However, we chose different
names since there is no validate - reset loop
in the general execution model of Ptolemy II (even
if such a validation steps exists in the “Continuous
Time” model of computation), and the names of these
methods denote the activation of a behavior. Our
execution model deals only with observations and we
do not limit the behavior of actors to the body of a
fire method.
3.5 Allowing Heterogeneity
The execution model we have just presented here uses
only one model of computation, so one may won-
der how heterogeneous models are handled. Our ap-
proach of heterogeneity is the same as the hierarchical
approach used in Ptolemy (Eker et al., 2002), and our
execution model does not depend on the models of
computation used to compute the behavior of the ac-
tors of a model. It is therefore possible to define the
behavior of actors using internal models of computa-
tion that differ from their external model of computa-
tion.
An issue still subsists: how data produced accord-
ing to the internal model of computation of an actor
will be interpreted in the context of its external model
of computation? The behavior of an actor may be ex-
pressed using properties that have no meaning in the
external model of computation. For instance, an ac-
tor may produce time-stamped data samples because
its behavior is defined using a timed model of com-
putation, and these samples may be read in a model
of computation that has no notion of time. In this
case, the series of timed-stamped data samples can be
viewed as a sequence of data samples just by discard-
ing the time-stamps, but in the reverse case, when data
with no time-stamp is produced in a timed model of
computation, a time-stamp must be created for each
data sample, and this requires additional information.
Our position is that there is no automatic way to
convert data (or control) from a model of computa-
tion to another. Often, there are standard ways of
adapting the semantics of two models of computa-
tion (for instance, periodic sampling can be used to
go from continuous time to synchronous data-flow),
but such transformations should not be “hard-coded”
in the modeling framework nor applied implicitly to
an heterogeneous model. The reasons for this are:
• implicit transformations are framework-dependent.
This means that the same model could adopt differ-
ent behaviors when executed in different modeling
frameworks;
• several transformations between two models of
computation may exist (for instance, when going
from discrete to continuous time, it is possible to
hold the last value, or to use linear or more com-
plex interpolation). The choice of a transformation
is part of the design of the system, and it should
therefore appear explicitly in the model;
• even when there is only one possible transforma-
tion between two models of computation, using this
transformation and setting its parameters is a de-
sign choice, and it should appear in the model of
the system, with the same importance as the mod-
els of computations.
A PRIMITIVE EXECUTION MODEL FOR HETEROGENEOUS MODELING
251

The main problem with such transformations is that
if they are implemented as actors, these actors ap-
pear either in the internal or in the external model of
computation. Both ways are wrong since they break
modularity: if the internal model of an actor contains
actors to adapt data to its external model of compu-
tation, this internal model depends on the external
model of computation. This means that the design
of an actor depends on the context in which it will
be used. The same problem occurs when the adapt-
ing actors are placed in the external model of com-
putation. In (Feredj et al., 2004), we presented a
model for domain-polymorph components that allows
the adaptation between two models of computation to
be done at the interface between the models. This ap-
proach turns the adaptation between the semantics of
the internal and external models of computation into
a property of the edge of the actor.
A last issue is that it is sometimes necessary to
define actors which obey several models of compu-
tation. For instance, a sampler has a continuous in-
put, a discrete event input (the sampling clock) and a
data-flow output (the sequence of samples). A level-
crossing detector has a continuous or sampled input
and a discrete event output. Such actors cannot be
handled directly in our execution model because only
one model of computation is allowed in the model of
a system. However, we have shown in (Boulanger
et al., 2004) that a flat heterogeneous model, i.e. a
model that uses several models of computation at the
same level of its hierarchy, can be rewritten automati-
cally into a hierarchical model by projecting heteroge-
neous actors on the models of computation they use.
One may also consider that such behaviors should not
be modeled as actors but as transformations between
models of computation, and considered as properties
of the edge of models, as evoked earlier.
4 CONCLUSION
We have presented the roles of a model of compu-
tation and the different kinds of actors it should be
able to manage, and then an execution model which,
by making as few assumptions as possible about ac-
tors, is able to execute models that obey any model of
computation. Our works on the integration of the re-
active synchronous approach into object-oriented pro-
gramming and on the adaptation between models of
computation in the Ptolemy framework make us quite
confident in the universality of this model. By consid-
ering only observations on the ports of actors, and not
the activity of actors, this execution model can safely
ignore what happens at lower levels of the hierarchy
of a model. This allows the use of different models
of computation at different level of the hierarchy of a
model of a system. Moreover, by allowing an actor
to veto the result of the computation of a snapshot of
the model, this execution model allows inner models
of computation to interact with the outer models, in
addition to the usual control that the outer model has
on the inner models of computation.
This execution model requires that a model of com-
putation is able to provide a schedule of the actors of
a model, and to propagate the data observed on the
output ports toward the input ports. These two op-
erations can be complex, and are, for the moment,
implemented using generic programming languages
like Java or C++. Our goal is to describe them for-
mally using either an extended version of the Object
Constraint Language (OCL) or the Action Language
of UML 2, with a mathematical foundation for the in
order, particularly, to define transformations from a
model of computation to another and to handle het-
erogeneity in a more generic way.
REFERENCES
Boulanger, F., Mbobi, M., and Feredj, M. (2004). Flat
heterogeneous modeling. In IPSI 2004 conference,
http://wwwsi.supelec.fr/fb/download/Articles/IPSI-
2004.pdf.
Brooks, C., Lee, E. A., Liu, X., Neuendorffer, S., Zhao,
Y., and Zheng, H. (2005). Heterogeneous concurrent
modeling and design in java (volume 1: Introduction
to ptolemy ii). Technical report, University of Califor-
nia, Berkeley.
Eker, J., Janneck, J. W., Lee, E. A., Liu, J., Liu, X., Ludvig,
J., Neuendorffer, S., Sachs, S., and Xiong, Y. (2002).
Taming heterogeneity the ptolemy approach. In Pro-
ceedings of the IEEE, Special Issue on Modeling and
Design of Embedded Software.
Feredj, M., Boulanger, F., and Mbobi, M. (2004).
An approach for domain polymorph component
design. In IEEE International Conference on In-
formation Reuse and Integration 2004 (IRI 2004),
http://wwwsi.supelec.fr/fb/download/Articles/IRI2004-
CDP.pdf.
Fleurey, F., Drey, Z., and Vojtisek, D. (2006). KerMeta
Manual. http://www.kermeta.org/docs/KerMeta-
Manual.pdf.
Kong, C. and Alexander, P. (2003). The rosetta meta-model
framework. In 10th IEEE International Conference
and Workshop on the Engineering of Computer-Based
Systems (ECBS’03).
Liu, X., Liu, J., Eker, J., and Lee, E. A. (2003). Hete ro-
geneous modeling and design of control systems. In
Software-Enabled Control: Information Technology
for Dynamical Systems. Wiley-IEEE Press.
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
252
