
ON ABILITY OF ORTHOGONAL GENETIC ALGORITHMS FOR
THE MIXED CHINESE POSTMAN PROBLEM
Hiroshi Masuyama
Information and knowledge Engineering, Tottori University, Koyama-cho Minami 4-101, Tottori, Japan
Tetsuo Ichimori
Information Systems, Osaka Institute of Technology, Kitayama 1-79-1, Hirakata, Japan
Toshihiko Sasama
Information and knowledge Engineering, Tottori University, Koyama-cho Minami 4-101, Tottori, Japan
Keywords: Orthogonal design, Genetic algorithm, Chin
ese postman problem, Postman’s route.
Abstract: The well known Chinese Postman Problem has many applications, and this problem has been proved to be
NP-hard in graphs where directed and non-directed edges are mixed. In this paper, in order to investigate the
salient feature of orthogonal design, we designed a genetic algorithm adopting an orthogonal crossover
seoperation to solve this (mixed Chinese Postman) problem and evaluate the salient ability. The results
indicate that for problems of small sizes, the orthogonal genetic algorithm can find near-optimal solutions
within a moderate number of generations. We confirmed that the orthogonal design shows better
performance, even for graph scales where simple genetic algorithms almost never find the solution.
However, only the introduction of orthogonal design is not yet effective for the Chinese Postman Problem
of practical size where a solution can be obtained in less than 104 generations. This paper concludes that the
optimal design scale of orthogonal array to this mixed Chinese Postman Problem does not conform to the
same scale as the multimedia multicast routing problem.
1 INTRODUCTION
The Chinese Postman Problem, as is well known, is
to find the shortest route in a graph that uses every
arc (directed or non-directed edge) and gets back to
where it started. For example in the non Eulerian
graph shown in Fig.1, since Postman’s route
traverses every arc at least once, the Postman must
passes doubly through an arc of weight 6. By
duplicating some arcs, the non Eulerian graph can
have at leaset one Postman’s route. In general, if a
given graph is a non Eulerian graph, it can be said
that the optimum solution of the Chinese Postman
Problem is a route where the total weight of
duplicated arcs is the minimum. When a given graph
is an Eulerian graph, the solution is uniquely
determined.
Though this problem has many applications,
in
cluding robot exploration and analyzing interactive
systems and web site usability (Thimbleby, 2003),
this problem has been proved to be NP-hard. The
multimedia multicast routing problem is also NP-
hard. Paper (Zhang and Leung, 1999) proposed an
orthogonal genetic algorithm for this latter problem,
and concluded on the basis of solving a benchmark
test problem, that for practical problem sizes the
orthogonal genetic algorithm can find near-optimal
solutions within a moderate number of generations.
Its salient feature is to incorporate an experimental
design method called orthogonal design into the
crossover operation. In order to further investigate
this salient feature of orthogonal design, which was
applied to the sampling of genes from the parents for
crossover, we will design a genetic algorithm
adopting an orthogonal crossover operation to solve
the mixed Chinese Postman Problem and evaluate
the salient ability.
For the problem which we treat is called the
C
hinese postman problem on mixed networks
(WCPP), heuristic solution procedures have been
proposed to solve approximately (Edmond and
Johnson, 1979)(Pearn and Liu, 1995)(Frederickson,
1979).
39
Masuyama H., Ichimori T. and Sasama T. (2006).
ON ABILITY OF ORTHOGONAL GENETIC ALGORITHMS FOR THE MIXED CHINESE POSTMAN PROBLEM.
In Proceedings of the First International Conference on Software and Data Technologies, pages 39-45
DOI: 10.5220/0001314600390045
Copyright
c
SciTePress
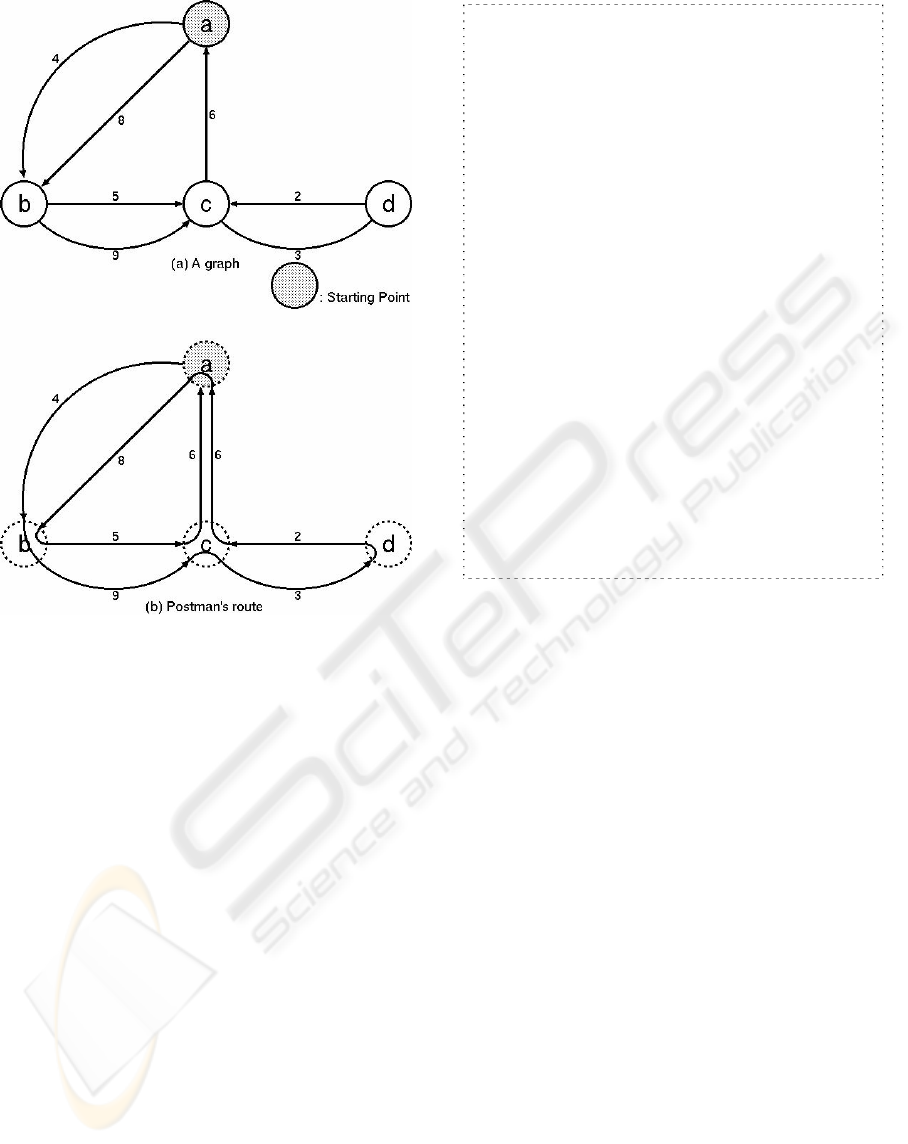
Figure 2: A basic process of genetic algorithm.
1. [Start] Generate random population of t
chromosomes (suitable solutions for the problem).
2. [Fitness] Evaluate the fitness f(x) of each
chromosome x in the population.
3. [New population] Create a new population by
repeating following steps until the new population
is complete.
1. [Selection] Select two parent chromosomes
from a population according to their fitness
(the better their fitness, the better their
chance of being selected).
2. [Crossover] Use crossover probability to
cross over the parents and form a new
offspring (children). If no crossover was
performed, the offspring would be an exact
copy of the parents.
3. [Mutation] Use mutation probability to
mutate new offspring at each locus (position
in the chromosome).
4. [Accepting] Place new offspring in a new
population.
4. [Replace] Use newly generated population to
continue the algorithm.
5. [Test] If the end condition is satisfied, stop, and
return the best solution in the current population.
6. [Loop] Go to step 2.
Figure 1: An example of route in Chinese postman
problem.
2 GENETIC ALGORITHM AND
ORTHOGONAL ARRAY
REPRESENTATION
A genetic algorithm (GA) is a heuristic approach
used to find approximate solutions to knotty
problems through application of the principles of
biological evolution. Genetic algorithms make the
best of biologically derived approaches such as
inheritance, mutation, natural selection, and
recombination (or crossover). Genetic algorithms are
a particular class of evolutionary algorithms where a
population of abstract representations (called
chromosomes) of candidate solutions (called
individuals) evolve into better solutions. That is,
information treated in GA can be classified into two
structures: phenotype and genotype. Phenotype
represents information in the biological world, and
genotype represents information in a population of
chromosomes. By encoding, the information in a
phenotype can be transferred into a genotype, and by
decoding the opposite occurs. We will chiefly
consider that in a genotype. Even though some
different encodings are possible, in general the
solutions are represented in binary strings of 0s and
1s.
In this mixed Chinese postman problem, we will
treat a given graph G whose every arc is a directed
edge or a non-directed edge. We will consider a
directed graph G’ where every non-directed edge in
the given graph is changed into two directed edges
with different directions each other. Then, we can
make our chromosome type as an integer string
whose element means the number of times that the
postman passes the arc. The length of a string is the
number of edges of G’. Therefore, in this mixed
Chinese postman problem, the solutions are
represented in strings of integer. The evolution starts
from a population of completely random individuals
and goes on in generations. In each generation, the
fitness of the whole population is evaluated, and
multiple individuals are stochastically selected from
the current population (by judging their fitness) and
modified (so called by mutation or recombination) to
form a new population, which becomes current in
the next iteration of the algorithm. The general
process of GA is known, and is shown in Fig.2.
Orthogonal array was developed to find the
smallest, yet most cost effective, and therefore best,
combination by which many and consumptive
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
40

combinations can be avoided (Fang and Wang,
1994). An orthogonal array is represented in
Table.1-1 by L
9
(3
4
), where 3, 4, and 9 mean the
number of kinds of entries, columns, and rows,
respectively. In general, we let L
m
(n
k
) denote an
orthogonal array for k factors, n levels, and m
combinations of level to be tested. Orthogonal arrays
can be systematically built. Label L comes
originally from a “Latin” square, which is defined as
a matrix where no two entries in a row (or a column)
have the same value. It has been proved that the
orthogonal design is optimal for use as an additive
model and a quadratic model, and that the selected
combinations are good representatives for all the
possible combinations (Wu, 1978). The problem of
building an orthogonal array is the same as the
problem of finding m nodes which are at the
maximum distance between any pair in the (k )-
dimensional hypercube. Table 1-2 shows 9 nodes
corresponding to 9 combinations (on an 8-
dimensional hypercube) in Table 1-1.
nlog
Table 1-1: A representation of orthogonal array L
9
(3
4
).
Table1-2: 9 nodes corresponding to 9 combinations on a
(k log n)-dimensional hypercube.
Combination Factor1 Factor2 Factor3 Factor4
1st 0 1 0 1 0 1 0 1
2nd 0 1 1 0 1 0 1 0
3rd 0 1 1 1 1 1 1 1
4th 1 0 0 1 1 0 1 1
5th 1 0 1 0 1 1 0 1
6th 1 0 1 1 0 1 1 0
7th 1 1 0 1 1 1 1 0
8th 1 1 1 0 0 1 1 1
9th 1 1 1 1 1 0 0 1
3 EXPERIMENTAL DESIGN
METHODS
In this section, we introduce the concept of
experimental design methods for our experiment
mentioned later.
3.1 Phenotype
Roads are modeled as a graph G = (V,E), where V is
a set of nodes and E is a set of arcs. By making
every non-directed arc express as two directed arcs,
change a given graph G into a directed graph G’. As
mentioned before, the optimum solution is a route
where the total weight of duplicated arcs is the
minimum. We number the edges in G’ from 1 to t.
We can then represent any route R of the graph G’
as an t-tuple (e
1
, e
2
, …, e
t
), where any element
(which means a gene) e
i
is defined as follows:
e
i
= The number of times that the postman passes
arc i
From the above definition, e
i
is a non negative
integer and can become 0 if e
i
is represented for one
of two directed edges changed from non-directed
edge in G. For example, assuming that edge with
weight 4 is r
4
, R in Fig.1(b) can be represented as
(e
r4
, e
r8
, e
r5
, e
r9
, e
r3
, e
r3
, e
r2
, e
r6
) =( 1, 1, 1, 1, 1, 0, 1,
2). Since R in Fig.1(b) is a Postman’s route, then this
phenotype ( 1, 1, 1, 1, 1, 0, 1, 2) is a solution.
3.2 Fitness
The Postman can return to the starting point if G is
an Eulerian graph. If G is a non Eulerian graph, in
order to return to the starting point the postman must
traverse some arcs more than once. In general, if G
is a non Eulerian graph, it can be said that the
optimum solution of the mixed Chinese Postman
Problem is a route where the total weight of
duplicated arcs is the minimum. When G is an
Eulerian graph, the solution is uniquely determined.
In order to set the fitness of the optimum solution
to maximum, we will prepare the following function
f of fitness.
⎩
⎨
⎧
=
otherwise ;0
route sPostman' hasG if arcs); gduplicatin of weight (total / 1
f
3.3 Orthogonal Crossover
In order to fit the mixed Chinese postman problem,
we interpret orthogonal array L
m
(n
k
) to be an
orthogonal array for k factors divided from n levels
(parent chromosomes), and m combinations of levels
(samplings at the time of crossover). Let orthogonal
Combination Factor1 Factor2 Factor3 Factor4
1st X X X X
2nd X Y Y Y
3rd X Z Z Z
4th Y X Y Z
5th Y Y Z X
6th Y Z X Y
7th Z X Z Y
8th Z Y X Z
9th Z Z Y X
ON ABILITY OF ORTHOGONAL GENETIC ALGORITHMS FOR THE MIXED CHINESE POSTMAN PROBLEM
41
array L
4
(2
3
) be shown in Table 2. Obeying the above
interpretation of L
4
(2
3
), 2 parent chromosomes are
divided into 3 factors each, and we obtain 4 new
chromosomes as shown in Fig.3 In the case of
L
9
(3
4
) , we obtain 9 new chromosomes from 4 parent
chromosomes as shown in Fig.4.
Table 2: Orthogonal array L
4
(2
3
).
Combination Factor1 Factor2 Factor3
1st X X X
2nd X Y Y
3rd Y X Y
4th Y Y X
Orthogonal crossover
X
) 11
213
201 ( )
(
) 21
211
201 ( )
(
) 21
213
110 ( )
(
)
11
211
110 ( )
(
3 2 1 4
3 2 1 3
3 2 1 2
3 2 1 1
= =
= =
= =
= =
x
y
y
O
y
x
y
O
y
y
x
O
x
x
x
O
, , ,
,
4 3 2 1
O O O O
Y
X
Children:
Parents:
( 110 211 11 )
( 201 213 21)
1
x
2
x
3
x
1
y
2
y
3
y
Y
Figure 3: Orthogonal crossover for L
4
(2
3
).
Figure 4: Orthogonal crossover for L
9
(3
4
).
3.4 Creation of the Initial
Population of Chromosomes
using an Orthogonal Array
In order to create the initial population of
chromosomes which resemble closely as possible as
they can, we will present a method to use an
orthogonal array in the creation of the initial
population of chromosomes.
A chromosome is an t-tuple whose the i-th
element is the number of times passing through the
i-th arc by the Postman’ route. Let divide a
chromosome into the number of factors. The range
of the random numbers is divided into the number of
levels of orthogonal array. In addition, for each one
of the same levels in orthogonal array select, let
randomly correspond to a random number in the
same range of the random numbers.
Let us take L
4
(2
3
) shown in table 3 and t=12 as
an example. Since a t-tuple is divided into 3 factors,
then we can represent 4 chromosomes based on
L
4
(2
3
) as follows:
X X X X X X X X X X X X
X X X X Y Y Y Y Y Y Y Y
Y Y Y Y X X X X Y Y Y Y
Y Y Y Y Y Y Y Y X X X X
Each X and Y are corresponded to a random
number in the ranges 0~6 and 7~12, respectively.
Then, we obtain the following initial population of
chromosomes (4 chromosomes) as an example.
1 3 5 3 5 4 2 4 5 5 4 6
5 6 4 2 7 9 8 9 10 7 9 11
8 10 9 7 2 5 1 4 11 8 9 10
7 11 8 9 10 7 8 12 2 5 1 3
11) 11 02 (11
1
X
x
x
x
x
4 3 2
21) 13 12 (20
4 1
Y
y
y
y
y
3 2
22) 11 01 (12
432 1
Z
z
z
z
z
) 11 13 01 12 ( ) (
) 22 11 12 12 ( ) (
21) 11 02 12 ( ) (
21) 11 01 20 ( ) (
11) 11 12 20 ( ) (
22) 13 02 20 ( ) (
) 22 11 01 11 ( ) (
) 21 13 12 11 ( ) (
) 11 11 02 11 ( ) (
43 2 1 9
43 2 1 8
43 2 1 7
43 2 1 6
43 2 1 5
43 2 1 4
4 3 2 1 3
43 2 1 2
43 2 1 1
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
x
y
z
z
O
z
x
y
z
O
y
z
x
z
O
y
x
z
y
O
x
z
y
y
O
z
y
x
y
O
z
z
z
x
O
y
y
y
x
O
x
x
x
x
O
Orthogonal crossover
Parents: X , Y , Z
Children: O
1
, O
2
, O
3
,
…
, O
9
4 EXPERIMENT
In this section, we will explain the experiments we
performed.
4.1 Graphs
We used random graphs shown in Table 4. We
applied the Genetic algorithm 30 times to each graph
and evaluated the mean values.
Table 4: Experimental graphs.
|V| |E| Total weight
5 7 44
4.2 Orthogonal Genetic Algorithm
(OGA)
We developed the following algorithm, as shown in
Fig.5, where an initial group starts from a population
of completely randomly generated individuals, and
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
42

the probabilities of crossover and mutation are 1.0
and 0.5, respectively.
Inputs: Graph G=(V,E), edge cost C(e) and node
degree deg(v)
Output: binary strings representing the Euler route
Step1) Initialization
Randomly create an initial generation of N
binary string P
0
= { X
1
, X
2
,…, X
N
}, X = {
x
1
, x
2
,…, x
k
}
and initialize the generation number gen
to 0.
* X is a chromosome, k = |V|
Step 2) Population Evolution
WHILE ( gen < MAX_GEN )
BEGIN
4.3 Simple Genetic Algorithm (SGA)
The simple genetic algorithm adopts a one-point
crossover in Step 2.1 instead of orthogonal
crossover.
4.4 Another Orthogonal Genetic
Algorithm using Orthogonal
Array in the Creation of the
Initial Population of
Chromosomes (OGA
2
)
This algorithm uses an orthogonal array also in Step
1 in Fig.5 instead of random number, and the
utilization method is shown in 3.4.
4.5 Results
Fig.6-1 shows the relationship between the number
of obtained Eulerian graphs and the number of
generations. On the other hand, Fig.7-1 shows the
relationship in the case where orthogonal array is
used in the creation of initial population of
chromosomes. Fig.6-2 shows the relationship
between the obtained minimum weight of the
Postman route and the number of generations.
Fig.7-2 shows the relationship in the case where
orthogonal array is used in the creation of initial
population of chromosomes. These results mean that
our orthogonal genetic algorithm shows better
performance, especially in L9(3
4
). SGA almost
never finds the solutions for Problem 3 where the
number of edges is 7.
For reader’s information, we show the
relationship between the number of generations and
the computation time required in 3 algorithms ( SGA,
OGA, and OGA
2
) in Tables 5 and 6.
In this mixed Chinese postman problem we
treated, in less than 10
4
generations we can obtain a
solution in graphs with nodes of less than 11.
However, we can’t obtain a solution in 2 or 3 days
for the larger sizes.
For reference we will show the data in the case of
non directed graphs G’’=(V’’, E’’), where |V’’|= 20,
|E’’|=30, total weight=178. The Chinese Postman
problem for non directed graphs belongs in Class P.
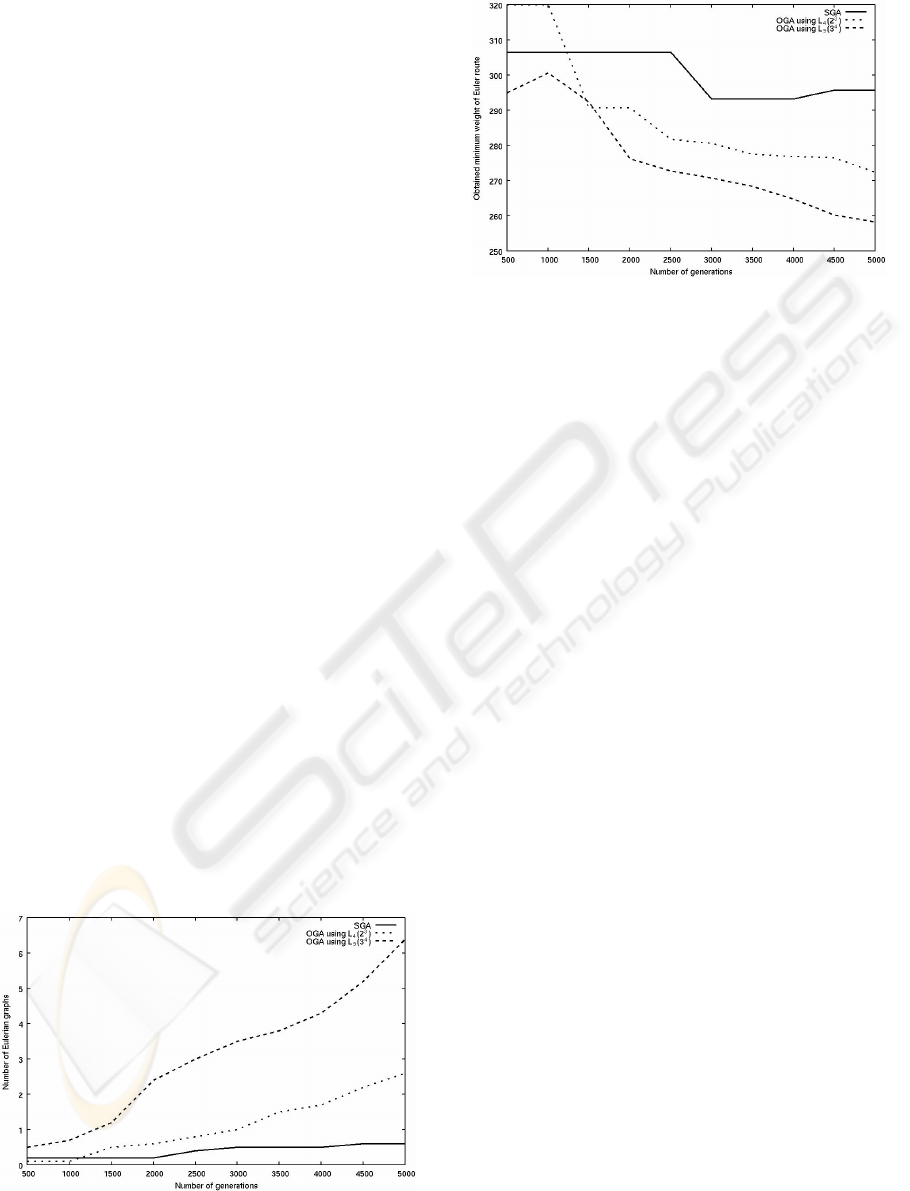
Figs.8-1 and 8-2 show the relationship between two
numbers of obtained Eulerian graphs and
generations, and the relationship between the
obtained minimum weight of the Postman route and
the number of generations, respectively.
Figure 5: A orthogonal genetic algorithm.
5 CONCLUSION
In order to investigate the salient feature of
orthogonal design, we designed a genetic algorithm
adopting an orthogonal crossover operation in the
mixed Chinese Postman Problem and evaluated the
salient ability. The orthogonal design shows better
performance, even for graph scales where simple
genetic algorithms almost never find the solution.
The experimental results show that, for problems of
non practical sizes, the orthogonal genetic algorithm
using the orthogonal array L
9
(3
4
) can find close-to-
optimal solutions within a moderate number of
generations. This optimal scale of orthogonal array
was confirmed for the multimedia multicast routing
problem of practical size (Zhang and Leung, 1999).
However, this orthogonal design is not yet effective
for the mixed Chinese Postman Problem of practical
sizes. For more effective computation, our one
possible extension of this research can be considered
as to incorporate the orthogonal array into the
DO N/2 times
BEGIN
Step 2.1) Orthogonal Crossover
Randomly select n parents strings from
P
gem
and perform orthogonal crossover
on them to generate m offspring o
1
,
o
2
,…, o
m
.
Step 2.2) Mutation
To perform mutation of offspring, flip
every bit in this string with a small
probability p.
Step 2.3) Select
Calculate the offspring fitness f, and
sort them by f, and choose n for the
next generation.
END
Step 3) Increment the generation number gem by 1.
END
ON ABILITY OF ORTHOGONAL GENETIC ALGORITHMS FOR THE MIXED CHINESE POSTMAN PROBLEM
43

0
10
20
30
40
50
60
70
80
90
100
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Number of
g
enerations
Number of Eulerian graphs
SGA
OGA using L4
OGA using L9
Figure 6-1: Relationship between two numbers o
f
obtained Eulerian graphs and generations.
0
20
40
60
80
100
120
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Number of
g
enerat ions
Obt ained minimum weight o
f
Euler route
SGA
OGA using L4
OGA using L9
Figure 6-2: Relationship between the obtained minimum
weight of the Postman route and the number of
generations.
0
10
20
30
40
50
60
70
80
90
100
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Number of
g
enerat ions
Number of Eulerian graph
s
N
o
n
Us
in
g
L4
Us
in
g
L
9
Figure 7-1: Relationship between two numbers o
f
obtained Eulerian graphs and of generations in the case
where orthogonal array is used in the creation of initial
population of chromosomes.
0
10
20
30
40
50
60
70
80
90
100
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
Number of
g
enerations
Obtained minimum weight of
Euler rout e
N
o
n
Us
in
g
L4
Us
in
g
L
9
Figure 7-2: Relationship between the obtained minimum
weight of the Postman route and the number o
f
generations in the case where orthogonal array is used in
the creation of initial population of chromosomes.
SGA
OGA
using
L
4
(2
3
)
OGA
using
L
9
(3
4
)
generation
time
(sec)
time
(sec)
time
(sec)
1000 247.1 279.8 437
2000 252.5 286.4 447
3000 257.8 292.6 456.6
4000 263.3 298.4 465.8
5000 268.3 304.4 475
6000 273.8 310.3 484.4
7000 279.1 316.2 493.6
8000 284.5 322.1 502.9
9000 289.9 328.1 512.5
10000 295.3 333.9 521.7
Table 5: Computation time required at 1000~10000
generations.
Table 6: Computation time required at 1000~10000
generations.
OGA
using
L
9
(3
4
)
OGA
2
using
L
4
(2
3
)
OGA
2
using
L
9
(3
4
)
generation
time
(sec)
time
(sec)
time
(sec)
1000 437 428.3 433.4
2000 447 437.7 443.2
3000 456.6 447.3 452.7
4000 465.8 456.4 462.3
5000 475 465.7 471.6
6000 484.4 474.7 480.9
7000 493.6 483.9 490.3
8000 502.9 493.1 499.5
9000 512.5 502.2 508.6
10000 521.7 511.4 517.9
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
44
experimental design methods of setting an initial
group of populations. We performed this extension.
The experiment results show no innovative
improvement.
REFERENCES
Thimbleby, H., 2003. The directed Chinese postman
problem. In Software - Practice & Experience, Vol.33,
No.11, pp.1081-1096.
Zhang, Q. and Leung, Y., 1999. An orthogonal genetic
algorithm for multimedia multicast routing. In IEEE
Trans. on Evolutionary Computation, Vol.3, No.1,
pp.53-62, April.
Fang, K.T. and Wang, Y., 1994, Number-Theoretic
Methods in statistics. New York, Chapman & Hall.
Wu, Q., 1978. On the optimality of orthogonal
experimental design. In Acta Mathematicae Sinica,
Vol.1, No.4, pp.283-299.
Sasama, T., Masuyama, H. and Ichimori, T., 2002. On
Fault Tolerance of Hypercubes using Subcubes. In Int.
Journal of Reliability, Quality and Safety Engineering,
Vol.9, No.2, pp.151-161.
Leung, Y., Li, G. and Xu, Z., 1998. A Genetic Algorithm
for the Multiple Destination Routing Problem. In
IEEE Trans. on Evolutionary Computation, Vol.2,
No.4.
Zhang, Q. and Leung, Y., 1999. An Orthogonal Genetic
Algorithm for Multimedia Multicast Routing. In IEEE
Trans. on Evolutionary Computation, Vol.3, No.1.
Edmond, J. and Johnson, E., 1979. Matching, Euler tours,
and the Chinese postman. In Mathematical
Programming, No.5, pp.538-554.
Pearn, W. L., and Liu, C. M., 1995. Algorithms for the
Chinese postman problem on mixed networks. In
Computers & Operations Research, Vol.22, No.5,
pp.479-489, May.
Frederickson, G.N., 1979. Approximation algorithms for
some postman problems. In J. Assoc. Comput. Mach.
Vol.26, pp.538-554.
Figure 8-1: Relationship between two numbers of obtained
Eulerian graphs and generations.
Figure 8-2: Relationship between the obtained minimum
weight of the Postman route and the number of
generations.
ON ABILITY OF ORTHOGONAL GENETIC ALGORITHMS FOR THE MIXED CHINESE POSTMAN PROBLEM
45
