
A GENERIC MODEL FOR CONNECTING MODELS IN
A MULTILEVEL MODELLING FRAMEWORK
Jan Pettersen Nytun
Agder University College
Faculty of Engineering, Agder University College
Grooseveien 36, N-4876 Grimstad, Norway
Keywords:
Megamodel, multilevel modeling, metamodeling, model weaving, model border.
Abstract:
In science and elsewhere models are weaved together forming complex knowledge structures. This article
presents a generic way of connecting models with model borders both vertically and horizontally in a mul-
tilevel modelling framework. One model can be connected vertically to several models allowing a model
element to be an instance of several metaclasses and different views can then be managed in an integrated
way. Models at the same level can also be connected by defining the correspondence between model elements.
The idea behind the approach is to break model architectures down to elementary building blocks so that all
parts that might be of interest become explicit and accessible.
1 INTRODUCTION
In this article some of the ideas behind a metamod-
elling framework called Semantic Integration World
Animation (Siwa) is presented; this framework is un-
der development at Agder University College and it
is meant for learning and experimentation; it is an
offspring of the SMILE project (Nytun et al., 2004)
which is more directed towards integration of exist-
ing language technologies.
MOF metamodel (OMG Editor, 2003) architec-
tures have a pyramid structure, while a Siwa architec-
ture is like a directed graph with models as nodes. The
graph is not cyclic except maybe for the top models
(e.g. level M3 in the UML metamodel architecture).
OMG has issued a request for revision of MOF
2.0 (OMG Editor, 2006a), some of MOFs restrictions
are becoming increasingly burdensome. MOF does
not allow properties to have an independent existence
and multiple classification is not possible - Siwa can
be used without these restrictions. It will also be pos-
sible to specify architectures that are not complete,
e.g. that a metamodel is missing; this opens up for
data analysis, reasoning about models and in some
cases the framework might automatically suggest a
metamodel.
Some models are static structures and some are ex-
ecutable models. We call the executable models se-
mantic engines, some sematic engines are presented
but they are not the main issue in this article.
A model is to a large extent defined by the role it
plays in relation to what it models; two basic roles are
defined by Thomas K
¨
uhne (K
¨
uhne, 2005): token and
type. A token model captures the singular aspects,
while a type model captures the universal aspects of
what it models. A class Buildingmight capture the
universal property that buildings have owners. An ob-
ject that models one specific building is a token model
for this building, e.g. it might capture the name of the
owner. The focus of this article is a technique for con-
necting models, the following model configurations
are to be supported:
Vertical (type model) This is the type model role
which spans two model levels (some would call this
the instanceOf-relation). Several models can
be type models for the same model instance; this is
not supported by MOF.
There are variations of this relationship, e.g. a
model instance might actually have been instanti-
ated from the model or the model is describing only
some aspects of the model instances.
Horizontal (token model) We see the need for a
model-to-model relationship which do not span a
level border, but is between two models that are
considered to be on the same level. Several mod-
els can in different way and with different level of
granularity and detail model the same thing; these
models are related with this relationship.
302
Pettersen Nytun J. (2006).
A GENERIC MODEL FOR CONNECTING MODELS IN A MULTILEVEL MODELLING FRAMEWORK.
In Proceedings of the First International Conference on Software and Data Technologies, pages 302-311
DOI: 10.5220/0001322303020311
Copyright
c
SciTePress

“Tom’s perception
of the Building”
:Building
id = “b1”
owner = “Tom”
TMBuilding
id
shape
type-
ModelFor
level N+1
level N
type-
ModelFor
Building
id
owner
token-
ModelFor
type-
ModelFor
Topographic map
Building register
Building Concept
token-
ModelFor
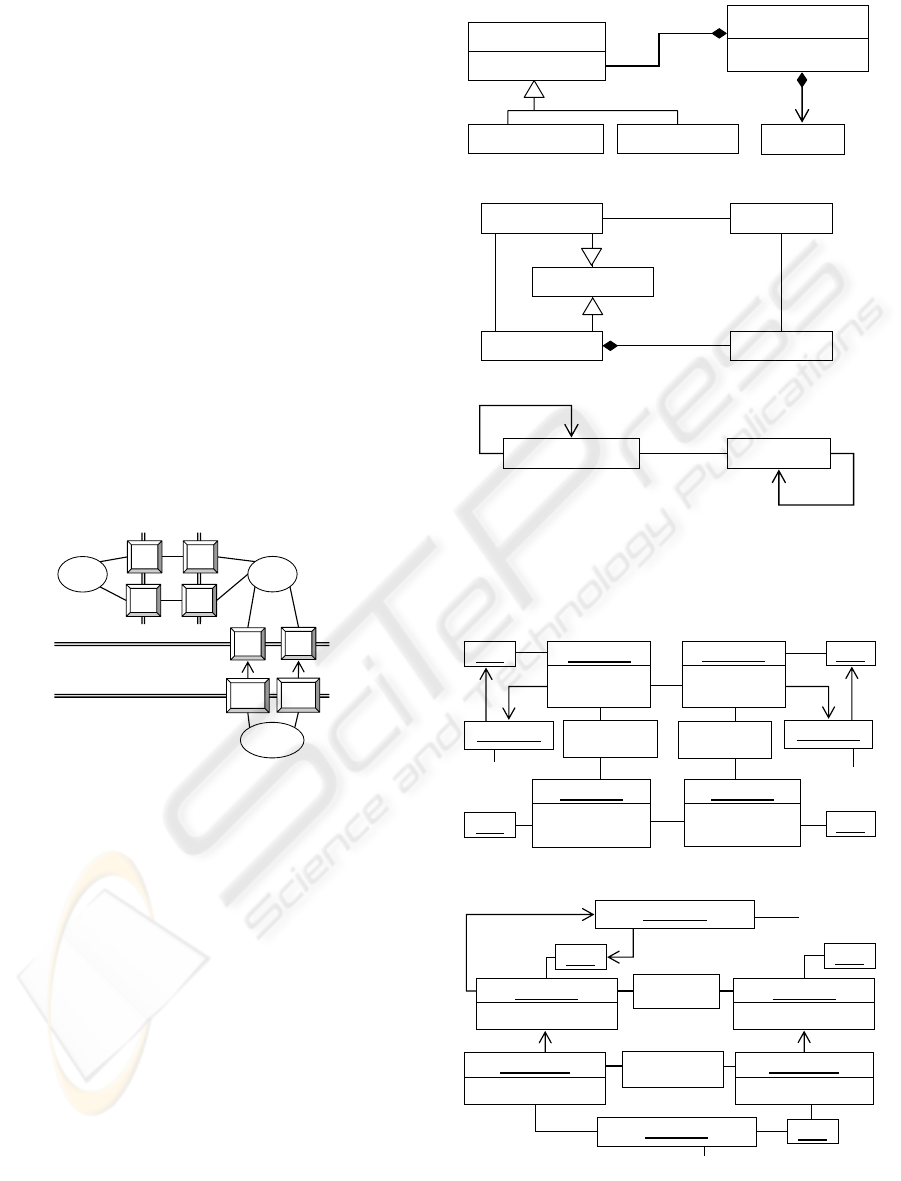
Figure 1: Example of token and type model.
Fig. 1 demonstrates, as we understand it, both to-
ken and type model roles (the UML notation has been
used in an ad hoc fashion).
The transitive property of the token model role can
also be seen in Fig. 1: the TMBuilding class is a
token model for class Building which is a token
model for ”the concept of a building”, consequently
TMBuilding is also a token model for ”the con-
cept of a building”. It seems to be a growing agree-
ment (K
¨
uhne, 2005; Favre, 2004a) that a metamodel
is a type model for another model which again is a
type model for its model instance. These models are
forming a stack structure where you don’t have the
same transitivity as for the token model role. Sub-
classing is a transitive relation and should not span a
level border (K
¨
uhne, 2005; Favre, 2004a).
UML has no diagram type that truly spans sev-
eral (metamodel) levels; UML object diagrams
shows instance specifications (instances of metaclass
InstanceSpecification) and also classes are
allowed; an object diagram is placed on the model
level (M1). As the name indicates, an instance speci-
fication is a specification and it might in fact specify
properties of several instances at the model instance
level (M0). According to this understanding, an object
diagram is correctly placed on M1because an instance
specification is not ”truly” in a horizontal relation to
an instance on M0. In our view, if a model is in a hor-
izontal relation to another model, then both models
are modelling ”exactly the same specific thing” even
if the number of details and precision might be differ-
ent; the models should consequently be placed on the
same level since they model the same thing.
The idea behind our approach is to break model
architectures down to elementary building blocks so
that all parts that might be of interest become explicit
and accessible; the framework should of course allow
the user to view an architecture at different levels of
granularity and with different concrete syntaxes that
hide the underling complexity.
Using the example in Fig. 1: object :Building
is
a structure that contains a slot called id with value
"b1" and a slot called owner with value "Tom";
we consider Building, id and owner to be sym-
bols that forms an upper border to the type model
containing class Building; we actually have two
borders (or border sides), one for each models being
connected, this allows different number of symbols
at the borders and it allows symbols to have different
names.
Sec. 2 presents our multilevel (meta-)modelling
framework and explains how models are connected.
In Sec. 3 we mention some related work. Sec. 4
presents an example of how Siwa can be used to do
testing of data consistency. We summarize and de-
scribe some research directions in Sec. 5.
2 THE SIWA APPROACH
Lately the term megamodel has been used to name
a model of MDE itself, e.g. by B
´
ezivin and
Favre (J. B
´
ezivin, 2004; Favre, 2005). Such a mega-
model describes the concepts of MDE - concepts like
model, metamodel and transformation. Fig. 2 shows
our preliminary megamodel which has been inspired
by Favre (Favre, 2005).
**
System
PhysicalSystem
AbstractSystem
model
system-
UnderStudy (sus)
Set
elements
sets
*
elementOf
DigitalSystem
SiwaWorld
*
horizontal vertical
modelOf
SiwaModel
*
Figure 2: Megamodel.
A GENERIC MODEL FOR CONNECTING MODELS IN A MULTILEVEL MODELLING FRAMEWORK
303

As we can see from Fig. 2 basically everything is
a system. In (Marcos Didonet Del Fabro, 2005b) a
system is described as a group of interacting, interre-
lated, or interdependent elements that form a complex
whole.
Abstract systems can only be described since they are
not to be found in the concrete; physical systems are
concrete and manifested ”in reality”. We consider a
computer system to be a special type of physical sys-
tem since they are manifested in computer hardware.
The Siwa framework supports the notion of levels
like you find it in metamodelling architectures defined
by OMG. Atkinson and K
¨
uhne (Atkinson and K
¨
uhne,
2001) have earlier used the term multilevel metamod-
elling, we prefer the term multilevel modelling frame-
work since an arbitrary number of levels will be sup-
ported including metamodel levels. We call a mul-
tilevel metamodel architecture defined in the frame-
work for a Siwa world. Fig. 2 defines a Siwa world
as a special type of digital system. A Siwa world is
composed of Siwa models which also are considered
to be special types of digital systems. The modelOf
relation comes in the two generic types: vertical and
horizontal.
A Siwa model can be a model for an abstract or
a physical system which is not part of a Siwa world.
This possible relation is not depicted in Fig. 2 since it
can not be explicitly represented in the framework.
Favre presents briefly the notion of static and dy-
namic system in (Favre, 2005), a Siwa world also has
these two aspects which we call: Model All Types
with Extent Realization (MATER) and Play Activa-
tions and Transformations with Extent Realizations
(PATER). The focus of this article is MATER and in
the following subsections MATER is presented with
the help of UML notation and examples. PATER is
touched in Sec. 4 when some sematic engines are de-
scribed.
In Subsec. 2.1 we present how to represent the in-
ternal structure of a Siwa model, in Subsec. 2.2 we
describe how Siwa models can be connected to con-
stitute a Siwa world (a multilevel model architecture).
2.1 Representing One Model
Fig. 3 presents the part of MATER that is used
when one model is to be represented, it is meant
to be used on all the levels of a Siwa world.
There are several similarities between this part of
MATER and MOF (OMG Editor, 2003) as an instance
model, e.g. an object can be represented as an in-
stance of Structure containing instances of Slot
with values representing properties of the object and
Descriptor can be used for type information as
described later. Links between objects can be repre-
sented as instances of Link. The property/owner as-
sociations can be used to represent relations between
sets; since there is no reference to a Descriptor,
instantiation of these associations might in some cases
lead to ambiguous situations when it comes to finding
their description on the level above. Fig. 3 has two
types of symbols:
Descriptor This symbol type is used to indicate clas-
sification and it is used to establish a vertical rela-
tion, e.g. structure describing a building called b1
might have a descriptor called Building.
Identifier An instance of Identifier is labeling
a part of the model being defined and functions as
an identifier for this structure, e.g. an identifier
b1 might reference structure that describes a build-
ing with that id. Another example would be an
identifier Building referencing a structure that
describes a class Building. Several identifiers
might reference the same structure; in some cases
this means that there are synonyms.
*
*
Structure
property
owner
*
*
*
*
Slot
Descriptor
*
1..*
{ordered}
Value
1..*
Link DataValue
{ordered}
val:String
target
Identifier
name:String
*
ident-
ified
1
*
Instance
name:String
Figure 3: Part of MATER: the internals of a Siwa model.
For us as humans the symbols are typically telling
what a model is about, from the ”framework point of
view” only what has been formalized and represented
in MATER ”does matter”.
An example of how an object of type Building
can be represented is given in Fig. 5. In Fig. 5(a)
the object is shown in UML notation, Fig. 5(b)
shows how MATER can be instantiated to represent
the same. Fig. 5(c) is showing an overview of the
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
304

Class
Property
name
isAbstract
name
multiplicity
Relationship
name
Association
Generalization
*
1
p
1
2
end
1
*
1
specific
*
general
generalization
g_s g_g
c_p
a_e
association
c
ModelElement
AssociationEnd
isNavigable
isComposite
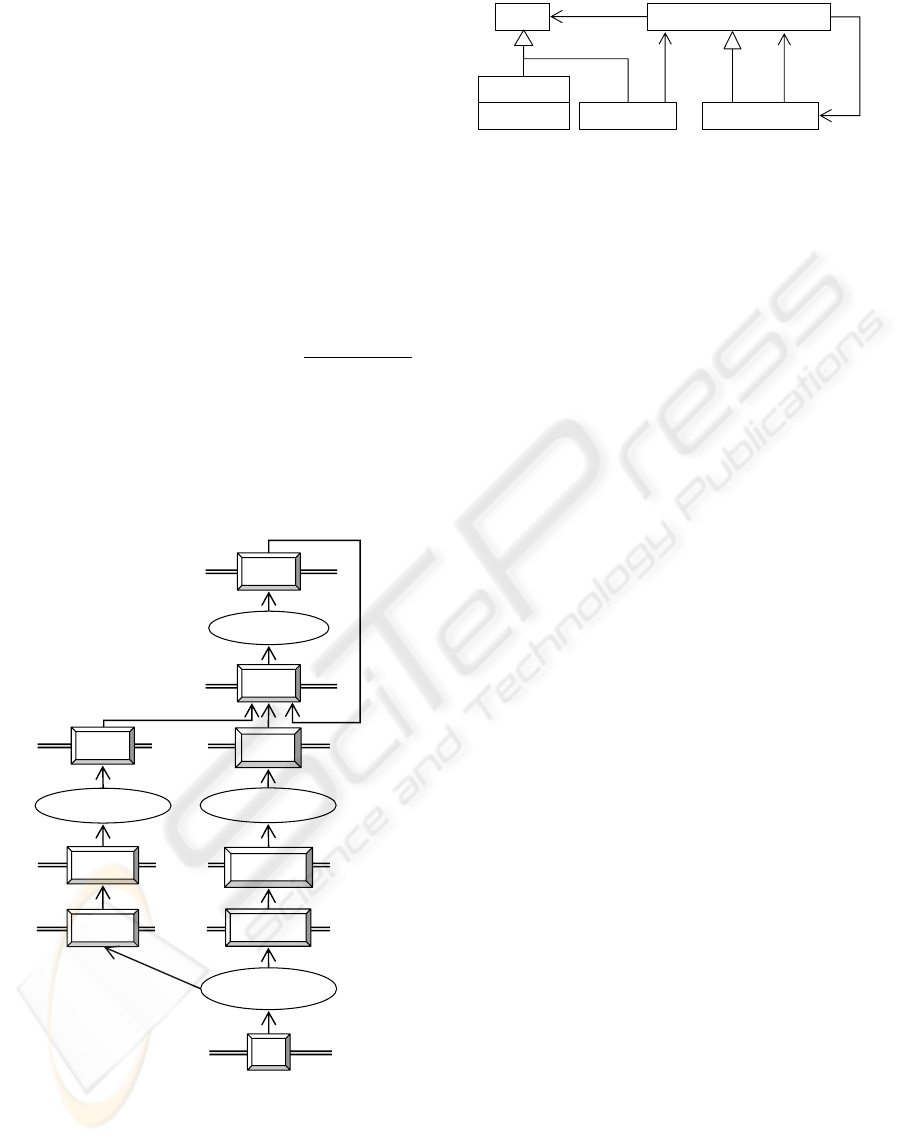
Figure 4: The top metamodel of the examples.
Building-object in an ad hoc notation where the
structure is hidden except for the symbols (two bor-
ders are shown, marked U and L, this concept will
be explained below). Fig. 4(a) shows the top model
which is called Class-MM. It describes important
object-oriented concepts like: abstract and concrete
class, property, multiplicity, association and general-
ization.
Fig. 6(a) shows a simple class called Building
with a property called id; Fig. 6(b) describes how
Class-MM can be instantiated to get the class and
then Fig. 6(c) demonstrates how MATER can be used
to describe the class (the :Property
-object is not
shown). As we can see from the figure the number of
model elements is huge - it correspond approximately
to the number one would get if the UML metamodel
was instantiated.
In the object-oriented literature, and also in this ar-
ticle, the difference between a class as a set (some-
thing abstract) and the description of a class is often
confused
1
. As a consequence of being abstract: it is
not possible to ”point to” a class and say ”there it is”,
but it might be possible to point to the instances of a
class and also to a description of a class
2
. MATER
does not have class as a built-in construction - there
is no model element in Fig. 3 called Class, but it is
possible to describe classes (e.g. Fig. 6(c)).
Seeing a class as an object is not in conflict with the
UML metamodel architecture since a UML model can
1
In our view reification is merely to establish a descrip-
tions of a concept.
2
The terms abstract class and concrete class used in
object-oriented programming is something else, in that con-
text a concrete class means that there are objects that are di-
rect instances of the class which is not the case for abstract
classes.
:Structure
:Slot
:DataValue
owner =”Tom”
:Identifier
name =”b1”
:Slot
:Descriptor
name=
”Building”
(a)
:Descriptor
:Descriptor
name =
”Building:id”
(c)
(b)
Structure of Model of Building
Building:id
b1
U
L
name=”Building:
owner”
Building Building:owner
:Building
id = “b1”
owner = “Tom”
Figure 5: Example of howto represent an object in MATER.
x
x
Building
id
name=“Building”
:Slot
:Identifier
:Descriptor
name=“Class”
:Descriptor
name=“Class:name”
:identified
:Class :Property
:c_p
:c :p
:Slot
:Descriptor
name=“Class:isAbstract”
:Descriptor
name=“class:p”
:Descriptor
name=“c”
:Link
:Descriptor
name=“c_p”
:Slot
“false”
:Slot
(a) (b)
:Structure
…
(c)
name=“Building”
isAbstract=“false”
name=“id”
isComposite=“true”
multiplicity=“1”
Figure 6: A part of the description of class Building.
A GENERIC MODEL FOR CONNECTING MODELS IN A MULTILEVEL MODELLING FRAMEWORK
305
be seen as composed of objects instantiated from the
UML metamodel (see (Atkinson and K
¨
uhne, 2002)
for more on this class/object nature); the UML meta-
model can again be seen as composed of objects in-
stantiated from MOF and MOF can be seen as com-
posed of objects instantiated from itself.
A class Building in a UML class diagram is an in-
stance of class Class of the UML metamodel, we
understand that Building will be a class when we
read about the semantics of class Class (OMG Ed-
itor, 2006b): A class is a type that has objects as its
instances...The instances of a class are objects. From
this description we understand that a whole UML
metamodel architecture can be depicted as an object
diagram, which is known from the literature (e.g. (Ny-
tun et al., 2004) and (Martin Gogolla, 2005)).
MATER offers several ways to model the same
thing and it is not ”strongly” constrained - this is de-
liberate and opens for experimentations. It is not dis-
cussed in the article but it will be possible to configure
the framework with the help of some OCL-like lan-
guage, e.g. enforce strict metamodelling (Atkinson
and K
¨
uhne, 2000).
M3
D1
D2
I5
I6
M2
U
L
I1
I2
H
M1
I3
I4
H
Figure 7: Sketch of connected models.
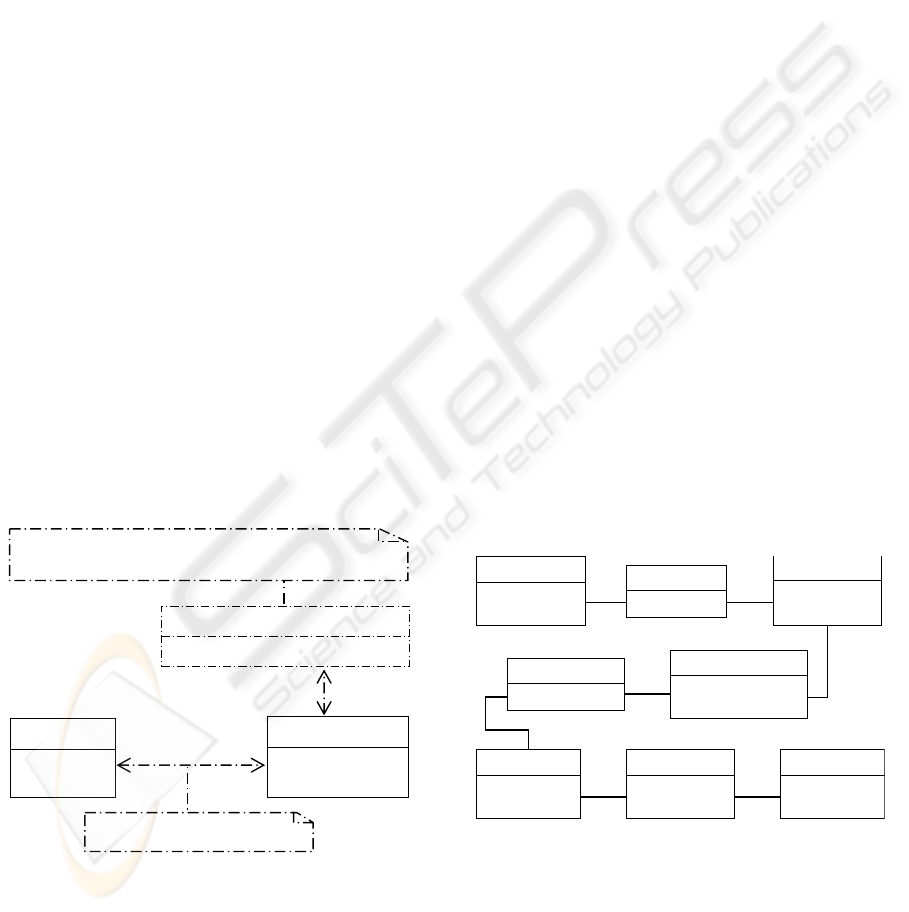
2.2 Connecting Models
Fig. 8 extends MATER and adds the possibility to
connect models. A Siwa model can contain borders;
two models are connected by connecting two borders,
one from each model. When the models to connect
are on the same level both borders will be of type
HorizontalBorder (Fig. 8(c)), when the models
are on different levels the border on the lower level is
of type UpperBorder (Fig. 8(b)) and the border of
the upper model is of type LowerBorder.
Fig. 7 offers a sketch where a model called M3 is
connected to a model M2 that resides on a level above.
M3 has an instance of UpperBorder (marked with
letter U) containing two instances of Descriptor
called D1and D2; these two symbols are connected to
instances of Identifier, I5 and I6 respectively;
*
SiwaModel
VerticalBorder
name:String
Border
HorizontalBorder
name:String
1
Instance
1
*
(a)
(c)
(b)
VerticalBorder
LowerBorder
UpperBorder Descriptor
Identifier
0..1
*
0..1
0..1
connected-
Identifier
connected-
Descriptor
1
*
HorizontalBorder Identifier
*
0..1
connected-
Identifier
0..1
0..1
0..1
0..1
0..1
0..1
connectedBorder
Figure 8: Part of MATER: connecting Siwa models.
:Descriptor
name=“Building:id”
:Structure
:Descriptor
name=“Building”
:Slot
Upper-
Border
:Identifier
name=“Building:id”
:Slot
:Identifier
name=“Building”
:Slot
Lower-
Border
:Identifier
name=
“Building:id”
:Slot
:Structure
:Identifier
name=
“Building”
:Slot
Horizontal-
Border
…
:Identifier
name=
“TMBuilding:id”
:Identifier
name=
“TMBuilding”
:Slot
:Structure
:Slot
…
(a)
(b)
:Structure
…
…
Horizontal-
Border
Figure 9: The example (incomplete) of Fig. 1 in MATER.
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
306
M2 has an instance of LowerBorder (marked with
letter L) containing both I5 and I6. Fig. 7 is
also demonstrating how model M1 and M2 residing
on same level are connected by two instances of
HorizontalBorder (marked with letter H).
The vertical association in Fig. 8(b) has multiplic-
ity 0..1 on the Identifier side, this means that
incomplete architectures, as claimed in the introduc-
tion, are possible. The claim that a model can have
several metamodels is justified by allowing several
upper borders for one and the same model.
Fig. 9 shows in more detail an example (same ex-
ample as in Fig. 1) of how MATER can be instantiated
to connect models, (a) shows how TMBuilding and
Building residing on the same level are connected,
while (b) shows how Building and :Building
residing on different levels are connected.
This way of connecting models is an extension to
what we have presented before; (Nytun et al., 2004)
presents a solution where two models would share a
common border instead of having one border for each
model to be connected; also the connecting of models
on the same level is new.
U
Object-M
Class
Object
L
. .
U
Class
Class-MM
Class
L
U
Class
Building
Building-M
L
Building-b1
b1
L
Building
U
Object
U
Figure 10: Architecture of building example
(TMBuilding is not included).
In Fig. 10 some of the models described above are
put together to form a multilevel architecture. The
only model that has not been mentioned before is the
one named Object-M; as can be seen in Fig. 11 it
*
.
.
Value
1..*
*
Link
*
DataValue
owner
0..1
val:String
.
target
Slot
property
*
1..*
belongsTo
Object
Figure 11: Model Object-M in detail.
simply defines an object as a structure having slots
with values and links to other objects. The instance
of Structure representing the building object has
both Building and Object as descriptor.
Model Object-M is introduced to demonstrate that
a model can have several type models. Object-
M could be used to define a more general XML format
than if Building-M was used.
3 RELATED WORK
Today there is much interest in the use of metamodels,
e.g. in MDA (OMG, 2003), MDE (Favre, 2004b),
LDD (Fowler, 2005), DSL (Greenfield et al., 2004).
The part of Siwa presented in this article, which is
mainly the static part, can be used as a starting point
in all the mentioned fields.
There are several other meta-modelling frame-
works, to mention a few: MetaEdit+ (Meta-
case, 2006), Coral (Marcus Alanen, 2004),
XMF (Tony Clark, 2004), EMF (EMF, 2006)
and MPS (MPS, 2006).
Rondo (S. Melnik, 2003) is a programming plat-
form for generic model management and it includes
high-level operators used to manipulate models and
mappings between models. AMW (Marcos Didonet
Del Fabro, 2005a) goes further and allows extensi-
ble mappings. AMW (Marcos Didonet Del Fabro,
2005a) is a generic model weaver that allows the spec-
ification of correspondences between model elements
from different models - models are in this way con-
nected with a model, e.g. correspondence Equals
might be established between the two id attributes
of classes TMBuilding and Building of Fig. 1.
Our approach has similarities with the aforemen-
tioned works, but we have not found a framework that
allows models and model levels two be connected so
freely as our approach does, e.g. the weaving of mod-
els described above can be achieved simply by intro-
ducing another model with borders to the models to
be weaved; this new model will describe the structure
of the correspondences, semantic engines can then
be defined to handle the semantics of the correspon-
dences; a somewhat related example is given below.
A GENERIC MODEL FOR CONNECTING MODELS IN A MULTILEVEL MODELLING FRAMEWORK
307
4 LEGACY DATA CONSISTENCY
AS EXAMPLE
Our article (Nytun and Jensen, 2003) focused on
the consistency problems that occur when previ-
ously uncoordinated, but semantically overlapping
data sources are being integrated. The paper pre-
sented techniques for modelling consistency require-
ments using OCL and other UML modelling ele-
ments. The paper also considered the automatic
checking of consistency in the context of one of the
modelling techniques. This section presents an out-
line of how Siwa can be applied to implement one of
these techniques and how automatic testing of consis-
tency can be performed.
4.1 Consistency Modelling and
Testing
Fig. 12 shows an integration of two legacy mod-
els, where one is a description of apartments (class
Apartment) and the other a description of build-
ings (class Building). The consistency require-
ments are as follows:
1. The number of apartments that is given as a prop-
erty in class Building should be equal to the
number of apartments with the same building id (at-
tribute bId).
2. One building should have at least one apartment,
and an apartment should belong to exactly one
building.
1..*
{cApartmentCount =
(building.apartmentÆsize() = building.apartmentCount)}
1
{apartment.bId = building.bId}
1
1
cApartmentCount:boolean
ConsistencyApartmentBuilding
bId
apartmentCount
Building
aId
bId
Apartment
Figure 12: Consistency between Apartment and
Building.
The elements with dash-dotted line style in Fig. 12
constitute what we call a consistency model, this
model is manually made by the user. When the con-
sistency model is established, consistency testing of
legacy data can be performed automatically. In our
case there is one legacy data source with information
about buildings and one about apartments. Consis-
tency testing results in a report revealing which legacy
data that do not fulfil the consistency requirements.
The association (Fig. 12) between Apartment and
Building, including the attached invariant ex-
pressed in OCL, constitute consistency requirement
two. When testing is performed on the legacy data,
a link is created between an Apartment and a
Building instance if the invariant is fulfilled; if the
multiplicity on the association is broken, this is re-
ported in the consistency report.
Consistency requirement one is specified with help
of class ConsistencyApartmentBuilding,
property cApartmentCount and its attached in-
variant. During testing instances of type Con-
sistencyApartmentBuilding are created and
linked to Building instances; slot cApartment-
Count will be set to the value that fulfils the invari-
ant; if the value is false then a consistency viola-
tion has occurred and will be reported. Note that links
between Building and Apartment instances are
traversed when the values of cApartmentCount
slots are set. From this example we can understand
that standard OCL-statements are used as production
rules when the consistency model is being automati-
cally instantiated.
4.2 Implementation in SIWA
In Siwa the consistency model can be seen as an in-
stance of the declarative domain specific language de-
scribed by the metamodel given in Fig. 13.
CClass
CProperty
name
name
constraint
*
1
CClassEnd
name
multiplicity
CClassAssociation
name
constraint
CProxyEnd1
name
CProxyEnd2
name
multiplicity
CAssociation
name
constraint
1
1
1
1
1
1
CProxyClass
name
legacySystem
*1
1
*
2
1
Figure 13: Consistency modelling metamodel.
In brief: The legacy classes Building and
Apartment have proxy classes to represent them
in the consistency model; a proxy class is an in-
stance of CProxyClass. Class Consistency-
ApartmentBuilding (Fig. 13) is an instance of
CClass; its property cApartmentCount is an
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
308

instance of CProperty, where the value of slot
constraint is the text:
cApartmentCount = (building.apartment→size() =
building.apartmentCount)
The association between ConsistencyApart-
mentBuilding and Building is represented
as an instance of CClassAssociation going
between the building proxy class and Consist-
encyApartmentBuilding.
The association between Building and
Apartment is represented as an instance of
CAssociation going between the two proxy
classes; the value of slot constraint for this
instance is the text:
apartment.bId = building.bId
Fig. 14 gives an overview of the complete archi-
tecture. The lowest level can be seen as one contigu-
ous model composed of legacy data and a consistency
model instance. The legacy models are on the other
hand not changed - the borders towards the consis-
tency model can be extracted automatically. From a
model management point of view this is considered
an advantage since it gives few models to manage (re-
member that the lowest level can be produced auto-
matically at will).
The format of this article does not give room for
presenting a complete picture of how Siwa solves the
problem at hand, but below is some information about
how the consistency model instance is automatically
created by a semantic engine.
A semantic engine is a Siwa model that exhibits be-
havior. A special type of semantic engines can be at-
tached to borders, they are called border engines and
are typically involved in instantiation. For simplicity
we can assumed that such engines are programmed in
Java since this is our implementation language. The
metamodeller has made a border engine and attached
it to border L4 (Fig. 14). Border U4 and L6 is cre-
ated by the engine when the modeller decides to make
a consistency model. The engine is also attaching a
premade border engine at L6, it is this engine that au-
tomatically produces the consistency model instance
and the consistency report when triggered. This last
engine is an adapted implementation of the algorithm
presented in (Nytun and Jensen, 2003).
This way of establishing the semantics can be seen
as a specific way of implementing deep characteriza-
tion; some see deep characterization as a natural part
of metamodelling (K
¨
uhne, 2005).
5 SUMMARY AND RESEARCH
DIRECTIONS
The MATER model presented in this article repre-
sent our understanding of what we mean by a mul-
tilevel model architecture; we have tried to make an
explicit representation of all elements that constitutes
such an architecture. Complex and advanced concepts
can then be built in a natural way by combining these
defined building blocks.
MATER can be seen as a metamodel by itself,
but we choose to see it as the physical carrier for
multilevel modelling architectures. This view allow
us to specify top models as we see needed, e.g. a top
model that gives properties separate existence.
The following is a list of features that in our view
makes Siwa a promising and unique framework:
• It is not strongly coupled to the instantiation found
in its implementation language, this allows a model
to have several type models each offering different
and useful information about the model.
• It is extremely generic which makes it adaptable to
many different modeling needs, e.g. it might allow
separate existence of properties.
• It is possible to have incomplete architectures, e.g.
XML documents might be loaded for analysis, and
then a model might be produced automatically (T.
Gjøsæter and J. P. Nytun and A. Prinz and M.
Snaprud and M. S. Tveit, 2006). This is typically
not possible in other frameworks due to their strong
coupling to instantiation in the selected implemen-
tation language.
Parts of our framework are already implemented
in the Eclipse framework (d’Anjou et al., 2004).
The first prototype is implemented by defining the
MATER model as a UML model in Eclipse and from
this we create an EMF Model; this looks like a trick
since we end up with having all the Siwa model lev-
els at one EMF level (Prinz et al., 2006), but it gives
us a jump-start and it automatically produces a lot of
useful code.
ACKNOWLEDGEMENTS
Thanks to Andreas Prinz, Vladimir Oleshchuk, Chris-
tian S. Jensen, Birger Møller-Pedersen and Arne
Maus for continuous inspiration and valuable discus-
sions.
A GENERIC MODEL FOR CONNECTING MODELS IN A MULTILEVEL MODELLING FRAMEWORK
309

REFERENCES
Atkinson, C. and K
¨
uhne, T. (2000). Strict Profiles: Why
and How. In UML 2000 - The Unified Modeling Lan-
guage, Advancing the Standard, volume 1939 of Lec-
ture Notes in Computer Science. Springer.
Atkinson, C. and K
¨
uhne, T. (2001). The Essence of Mul-
tilevel Metamodeling. In UML 2001 - The Unified
Modeling Language: Modeling Languages and Appli-
cations, volume 2185 of Lecture Notes in Computer
Science. Springer.
Atkinson, C. and K
¨
uhne, T. (2002). Rearchitecting the
UML infrastructure. ACM Transactions on Computer
Systems (TOCS),, 12(4):290–321.
d’Anjou, J., Fairbrother, S., Kehn, D., Kellermann, J., and
McCarthy, P. (2004). The Java Developer’s Guide to
Eclipse. Addison-Wesley.
EMF (2006). EMF, the Eclipse Modelling Framework:
Available at: http://www.eclipse.org/emf.
Favre, J. (2004a). Foundations of meta-pyramids: Lan-
guages vs metamodels. Available at:
http://www.citeseer.ist.psu.edu
/722867.html.
Favre, J. (2004b). Foundations of model (driven) (reverse)
engineering - episode i: Story of the fidus papyrus
and the solarus. Available at:
http://www.citeseer.ist.psu.edu/
favre04foundations.html.
Favre, J.-M. (2005). Megamodelling and etymology. In
Dagstuhl Seminar 05161 on Transformation Tech-
niques in Software Engineering. Available at:
http://www-adele.imag.fr/ jmfavre.
Fowler, M. (2005). Language workbenches: The killer-app
for domain specific languages? Available at:
http://www.martinfowler.com/articles/
languageWorkbench.html.
Greenfield, J., Keith Short, w. c. b. S. C., and Kent, S.
(2004). Software Factories: Assembling Applications
with Patterns, Frameworks, Models & Tools. John Wi-
ley & Sons.
J. B
´
ezivin, F. Jouault, P. V. (2004). On the need of meg-
amodels. In OOPSLA, 2004.
K
¨
uhne, T. (2005). What is a model? In B
´
ezivin, J.
and Heckel, R., editors, Language Engineering for
Model-Driven Software Development, number 04101
in Dagstuhl Seminar Proceedings. Available at:
http://drops.dagstuhl.de/opus
/volltexte/2005/23.
Marcos Didonet Del Fabro, Jean B
´
ezivin, F. J. E. B.
G. G. (2005a). AMW: a generic model weaver. In
Proceedings of the 1re Journe sur l’Ingnierie Dirige
par les Modles (IDM05). Available at:
http://www.sciences.univ-nantes.fr
/lina/atl/publications/.
Marcos Didonet Del Fabro, Jean B
´
ezivin, F. J. P. V.
(2005b). Applying generic model management to
data mapping. In Proceedings of the Journes Bases
de Donnes Avances (BDA05). Available at:
http://www.sciences.univ-nantes.fr
/lina/atl/publications/.
Marcus Alanen, I. P. (2004). The Coral Modelling Frame-
work. In Koskimies, K., Kuzniarz, L., Lilius, J., and
Porres, I., editors, Proc. of the 2nd Nordic Workshop
on the Unified Modeling Language NWUML’2004.
Turku Centre for Computer Science, Finland.
Martin Gogolla, Jean-Marie Favre, F. B. (2005). On squeez-
ing m0, m1, m2, and m3 into a single object diagram.
In Workshop on Tool Support for OCL and Related
Formalisms - Needs and Trends OCL at Models 2005.
Available at:
http://www-adele.imag.fr/ jmfavre
Metacase (2006). MetaEdit+. Available at:
http://www.metacase.com/
MPS (2006). Meta programming system. Available at:
http://www.jetbrains.com/mps/.
Nytun, J. P. and Jensen, C. S. (2003). Modeling and Test-
ing Legacy Data Consistency Requirements. In UML
2003 - The Unified Modeling Language: Modeling
Languages and Applications, volume 2863 of Lecture
Notes in Computer Science, pages 341–355. Springer.
Nytun, J. P., Prinz, A., and Kunert, A. (2004). Represen-
tation of levels and instantiation in a metamodelling
environment. NWUML 2004.
OMG (2003). Model Driven Architecture Guide, Version
1.0.1. Object Management Group. omg/03-06-01.
OMG Editor (2003). Revised Submission to OMG RFP
ad/2003-04-07: Meta Object Facility (MOF) 2.0 Core
Proposal. Available at
http://www.omg.org/docs/formal
/06-01-01.pdf.
OMG Editor (2006a). MOF Support for Semantic Struc-
tures, OMG RFP ad/2006-06-03. Available at:
http://www.omg.org/docs/ad
/06-06-03.pdf.
OMG Editor (2006b). UML 2.0 Infrastructure Specifica-
tion, OMG Document formal/05-07-05 . OMG Docu-
ment. Available at: http://www.omg.org.
Prinz, A., Nytun, J. P., Chen, L., and Wei, S. (2006).
Integration of MATER and EMF. In Proc. of the 4th
Nordic Workshop on the Unified Modeling Language
NWUML’2006. Available at:
http://osys.grm.hia.no/osys/archive
/conferences/nwuml
06.
S. Melnik, E. Rahm, P. A. B. (2003). Rondo: A program-
ming platform for generic model management. In In:
SIGMOD, pages 193–204.
T. Gjøsæter and J. P. Nytun and A. Prinz and M. Snaprud
and M. S. Tveit (2006). Modelling accessibility con-
straints. In Proc. of ICCHP.
Tony Clark, Andy Evans, P. S. J. W. (2004). Applied Meta-
modelling. A Foundation for Language Driven Devel-
opment. Xactium. Available at:
http://www.xactium.com.
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
310
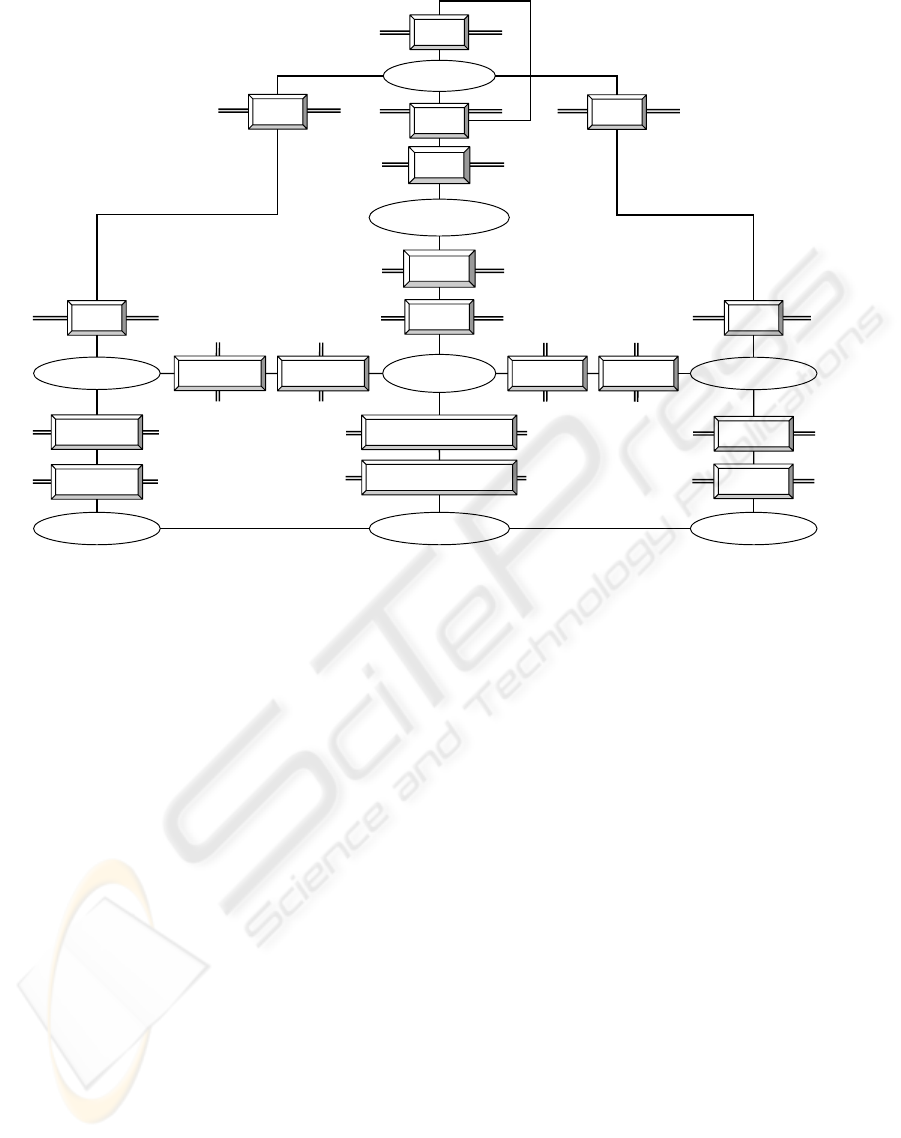
U3
Apartment-M
Class
Apartment
L5
..
U1
Class
Class-MM
Class
L2
U2
Class
CClass
Consistency-MM
L4
Consistency-M
CApartmentBuilding
L6
CClass
U4
Apartment
Apartment
BuildingBuilding
U5
Building-M
Class
Building
L7
Apartment
U6
Apartment-MI
Building
Building-MIConsistency-MI
CApartmentBuilding
U7
H1
H2 H3
H4
U8
..
Class
..
Class
L1 L3
Figure 14: Architecture example: consistency modelling and testing.
A GENERIC MODEL FOR CONNECTING MODELS IN A MULTILEVEL MODELLING FRAMEWORK
311
