LOCAL CONTROL FOR TEMPORAL EVOLUTION OF

TEXTURED IMAGES

Francesca Taponecco

Darmstadt University of Technology

Dept. of Computer Science, Computer Graphics Group

Fraunhoferstr. 5, 64283 Darmstadt, Germany

Keywords:

User-controlled texture-based visualization, ﬂow visualization, image-based rendering, texture synthesis, nat-

ural and non-homogeneous textures.

Abstract:

We present a novel algorithm that allows producing animated textures. The basic pattern of the texture is

given by an example and by a vector control ﬁeld that deﬁnes how anisotropic textures have to be adapted

and deformed locally. By changing this vector control ﬁeld over time, animations and variations of the texture

can be generated. The method is simple, general and allows managing control and manipulation. Signiﬁ-

cant applications can be found in producing textures in motion, in generating dynamic features’ variation in

non-homogeneous textures, and, especially, in visualizing time-varying image-based rendered ﬂow ﬁelds for

scientiﬁc visualization.

1 INTRODUCTION

Textures are fundamental for many applications

in computer graphics, computer vision and image

processing. Since many years, the analysis, recog-

nition and synthesis of textures are very active and

productive areas of research. Textures are useful for

many applications, especially, as they enrich synthetic

objects and computer generated scenes with variety

and realism, helping perception of shape, curvature

and material.

Objects appearance can be inﬂuenced by several

surrounding circumstances over time, and, as such,

temporal texture synthesis plays a fundamental role.

In addition, controllability is a crucial point to gener-

ate desires outputs.

In this paper, we present a ﬂexible methodology for

controllable synthesis of time-varying textures. The

objective is to animate textures in a general way, gen-

erating motion along given directions and simultane-

ously inﬂuencing the texture’s appearance in a dy-

namic way. The proposed algorithm allows produc-

ing a variety of outputs and provides a smooth and

continuous frames’ temporal animation.

Essentially, the novelty and contribution of this

work is to provide a straightforward methodology to

perform the synthesis of dynamic textures in a user-

deﬁned way: such approach permits intuitive image-

based texture synthesis enriched by a variety of cus-

tomizable effects. In particular, our method allows

local control to change the texture resolution, beside

its color and other attributes.

The paper is organized as follows: in the next sec-

tion we introduce previous research done in this area,

indicating the differences with our work. In chapter 3,

we introduce our approach and explain the algorithm.

In chapter 4 we present some obtained results. We

consider advantages and limitations, and we describe

attempts for optimizations. In chapter 5 we suggest

extensions and ﬁelds of application, discussing our

present and ongoing work. Finally, we conclude with

a summary and main contribution of the paper.

2 MOTIVATION AND RELATED

WORK

Signiﬁcant techniques have emerged in the computer

graphics and image processing literature; much effort

has been invested in producing useful and effective

algorithms, nevertheless, the need for visualization of

variable complex phenomena requires further investi-

gation.

Methods have been developed to generate dynamic

textures. In particular, we review here on existing ap-

285

Taponecco F. (2006).

LOCAL CONTROL FOR TEMPORAL EVOLUTION OF TEXTURED IMAGES.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 285-292

DOI: 10.5220/0001350502850292

 SciTePress

proaches for the synthesis of time-varying textures,

while we refer you to some good and comprehensive

surveys on texture synthesis procedures for a general

description and the basics of static textures. See for

instance (Efros and Leung, 1999), (Dischler et al.,

2002).

2.1 Motion in Texture Synthesis

Although many advances have been achieved in tex-

ture synthesis, the lack of control still remains a fo-

cal issue in designing new synthesis techniques. As

recognized by (Lefebvre and Hoppe, 2005), most

techniques that offers some kind of control, only pro-

vide little amount of texture variability and are mainly

restricted to random seeding of boundary conditions,

obtaining rather unpredictable results. Lefebvre and

Hoppe propose texture variability, but their target and

approach differs from ours. They desire an aperiodic

inﬁnite texture that they modify introducing new ele-

ments via drag-and-drop. (Kwatra et al., 2005) visual-

ize textures controlled through a ﬂow ﬁeld. Neverthe-

less, the approaches are basically different: they use a

global synthesis optimization process, which takes ef-

fect on the whole output texture, while we want local

control and we can manage several texture attributes

(such as resolution, color, shading, embossing besides

orientation) in a general way, in order to provide addi-

tional degrees of freedom for controlled synthesis of

the evolution of texture ﬂow and texture variation.

Regarding statistical methods that model textures

in motion and produce a sort of variation in textures,

they mainly concentrate on repetitive processes and

deal with the modelling and reproduction of tempo-

ral stationarity, like in sea-waves, smoke, steam, fo-

liage, whirlwind but also talking faces, trafﬁc scenes

etc. (see Figure 1). These approaches typically sug-

gest to use a sequence of textured frames to simulate

cyclic motion or periodic effects that are in some way

similar to movement.

For this task, an input sequence of samples - input

movie - is needed. This input has the function of train-

ing data, from which the procedures directly acquire

the necessary information and reproduce it through

statistical learning in an output sequence.

The ﬁrst approach that gives a statistical character-

ization of textures is the early work of Julesz (Julesz,

1962); successively, about twenty years ago, he intro-

duced (Julesz, 1981) the concept of textons as ”puta-

tive elementary units of texture perception” and there-

with opened the road to a very extensive research, also

in the ﬁeld of modelling motion in texture.

In recent years, Wei and Levoy (Wei and Levoy,

2000) propose a 3d extension to their model to cre-

ate solid textures or, as particular case, temporal tex-

tures, in case the motion data is local and station-

ary both in space and time. Bar-Josef et al. (Bar-

Figure 1: Temporal regularity is exploited in animation of

clouds, smoke, ﬁre, steam, waves, waterfall.

Joseph et al., 2001) employ multi-resolution analysis

(MRA) of the spatial structure of 2d textures and ex-

tend the idea to dynamic textures (movie texture), they

directly analyze a given input movie and generate a

similar one through statistical learning. Akin to this,

Pullen and Bregler (Pullen and Bregler, 2002) pro-

pose, modelling local dynamics, a multi-level sam-

pling approach to synthesize motion textures:new

(cyclic) motions that are statistically similar to the

original. Li et al. (Li et al., 2002) propose a tech-

nique named motion texture for synthesizing human-

ﬁgure motion: they model a motion texton by a Lin-

ear Dynamic System (LDS). Schdl et al. (Schoedl

et al., 2000) also model textons with LDS for video

texture, looping the original frames in a manner that

the synthetic reproduction is minimally noticeable to

the user. Doretto et al. (Doretto et al., 2004) generate

dynamic textures. Dynamic textures are sequences of

images of moving scenes that exhibit temporal regu-

larity, intended in a statistical sense. In the speciﬁc

case of spatially coherent textures (textures that ex-

hibit temporal statistics), Soatto et al. (Soatto et al.,

2001) (and (Doretto et al., 2004) for both spatial and

temporal regularity) synthesize a homogenized ver-

sion of the original sequence, through a model de-

signed for maximum-likelihood or minimal predic-

tion error variance. They use LDS to model a tex-

ture by an auto-regressive, moving average (ARMA)

multi-scale process. Similarly, Fitzgibbon (Fitzgib-

bon, 2001) uses an autoregressive (AR) model. Again

for stationary data, Szummer and Picard (Szummer

and Picard, 1996) use a spatial-temporal autoregres-

sive model (STAR), which provides a base for both

recognition and synthesis. This model produces con-

vincing results, nevertheless, it cannot capture curva-

ture and rotational motion.

Modelling more complex variations - nonlinear dy-

namics - is difﬁcult, it requires the use of multiple lin-

ear systems, and thus it is still challenging (see (Li

et al., 2002)).

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

286

3 ANIMATING TEXTURED

IMAGES

The works cited above mainly consider sequences

of images that exhibit certain stationary properties,

speciﬁcally repetitivity or cyclicity, in time. A prob-

lem is that the synthesized motion may lack global

variations when the training data is limited. These

techniques require a starting frames’ sequence, or in-

put movie, which has to be learned from the system

and then reproduced. Therefore, these methods par-

ticularly focus on statistical learning, having as task

texture analysis and recognition besides texture syn-

thesis. They usually assume the texture to have been

generated from an unknown stochastic source process

that they need to estimate and model.

3.1 Approach

Also for this reason, our work is different from the

ones described above. Our intention is not con-

strained to reproduce repetitive or cyclic motions; we

want to model general animations and variations of

textures. Instead of visualizing cyclic processes such

as repetitive waves, we concentrate on distorting a

given pattern by progressively varying some of the at-

tributes that deﬁne its structure. Starting with an input

texture, a control ﬁeld and an suitable synthesis algo-

rithm, it is possible to arbitrarily modify textures in

a variety of ways and then to continuously animate

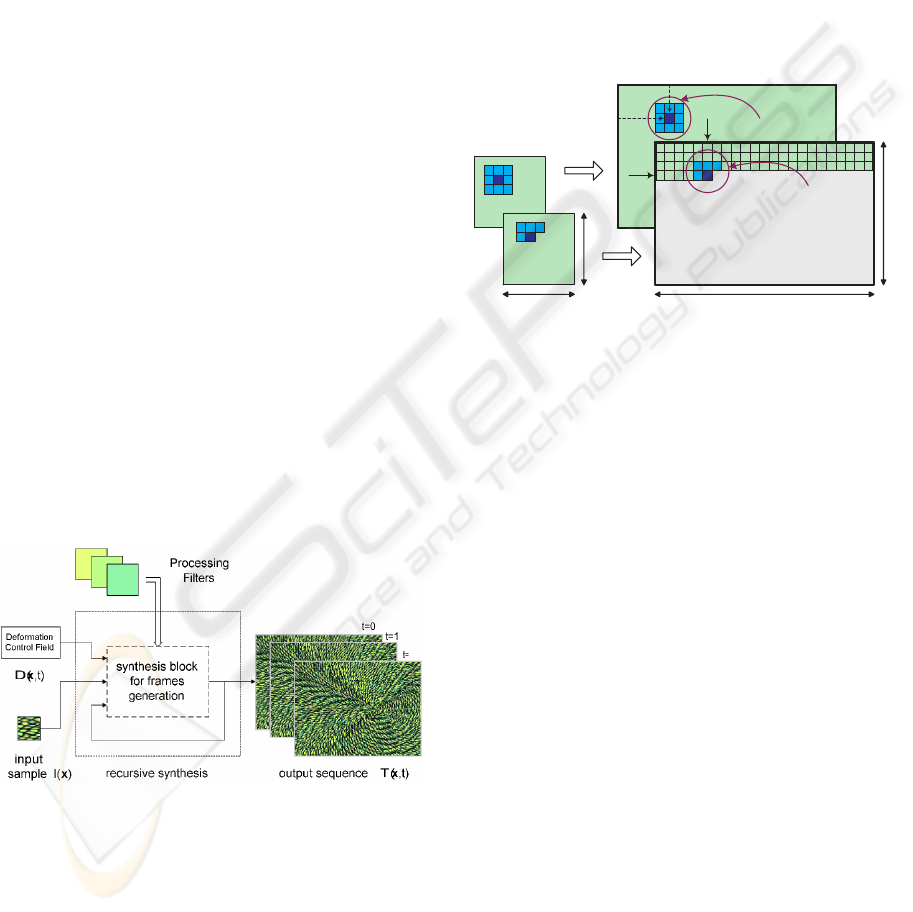
this transformation. Brieﬂy, we synthesize a frames

sequence that depicts the evolution of a texture over

time.

Figure 2: Block diagram for the generation of multiple sub-

sequent frames: their animated succession generates a time

varying texture.

Our algorithm works at a per-pixel level, and the

synthesis is performed in multi-resolution. Refer to

(Bonet, 1997), (Heeger and Bergen, 1995), (Portilla

and Simoncelli, 1999) for a complete explanation

about multi-resolution sampling procedures for tex-

ture synthesis.

3.2 Field-driven Synthesis

The motion and variation in time are controlled

through the selection of a control ﬁeld. This ﬁeld

is potentially multi-valued and multi-dimensional; it

varies the texture’s structure aligning and adapting

it along new directions. Such vector ﬁeld is vari-

able over time, hence, at each time step, the synthesis

process produces a corresponding texture frame. User

intervention is allowed in deﬁning the ﬁeld to inﬂu-

ence a given example. In this way, textures may be

arbitrarily controlled, deformed, varied over time.

t = 0

t = 1

t = 0

t = 1

Win

Wout

Hin

Hout

squared

neighbourhood

L-shaped

neighbourhood

Figure 3: Synthesis schema for the generation of two suc-

cessive frames using neighborhood size = 3.

3.3 Recursive Passes

The block scheme of Figure 2 sketches the generation

of the outputs’ sequence.

We recursively iterate the synthesis a desired num-

ber τ of frames. The dashed block representing

the single frame generation (used for standard tex-

ture synthesis) has been appropriately extended to

additionally acquire information from the previous

synthesized frame. For this scope, we deﬁne a

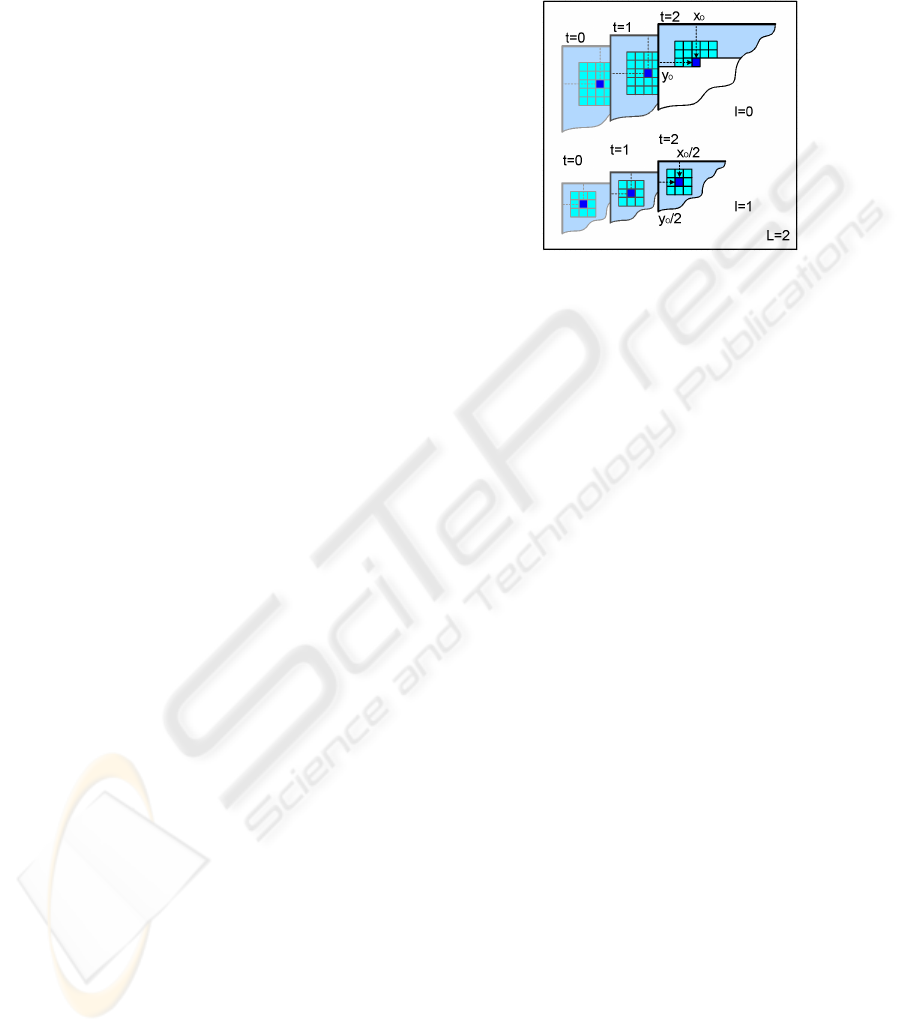
novel model for the neighborhood: we build a three-

dimensional cubic structure around the pixels. Fig-

ure 3 shows how to construct spatio-temporal neigh-

borhoods; it illustrates three-sized models in single-

resolution. Figure 4 shows a ﬁve-sized model in

multi-resolution.

Let consider the current pixel to synthesize, then

its cubic neighborhood incorporates the adjacent pix-

els in the L-shaped neighborhood - spatial informa-

tion - plus a number of square-shaped neighborhoods

- temporal information - at corresponding location

from the underlying complete layers at previous time

steps.

Such neighboring pixels carry coherence informa-

tion; in this way, this synthesis procedure achieves

continuity and preserves smoothness in the spatial do-

main (x, y) and in the temporal domain t as well.

LOCAL CONTROL FOR TEMPORAL EVOLUTION OF TEXTURED IMAGES

287

In the following section, we give more details for

possible re-implementation.

3.4 Algorithm

We call I(x) the selected input sample and deﬁne

T (x) to be an output texture in desired resolution,

where x is a vector, for simplicity in two-dimensions:

x =(x, y). Our target is to generate an animation of

T (x) under the action of a control ﬁeld D(x,t) and

during an arbitrary period of time τ : t ∈ [τ ] (see Fig-

ure 2).

The basic pattern of the texture is controlled

through the time-varying deformation ﬁeld and its

features are potentially controlled through ad hoc de-

ﬁnition of transfer functions T (x,t). More precisely,

D(x,t) and T (x,t) inﬂuence the speciﬁed texture ex-

ample over time, respectively by forcing it along new

directions, and by modifying its appearance.

For simplicity, we ﬁrst explain the temporal anima-

tion scheme; we illustrate later in section 3.6 how to

combine it with ﬁlter transformations.

Formally, we synthesize a texture’s sequence

T (x,t), with t =0, 1, ..., τ , and T (x) ∈ R

.As

drafted below in sub-section 3.5, we generate this

frames’ set in an automatic way with a recursive sys-

tem (refer to Figure 2): each temporal frame is in-

ﬂuenced in a straightforward manner by information

derived from the previous frame (or from a set of pre-

vious frames), this facilitates achieving smoothness

along the temporal evolution.

Figure 3 illustrates the synthesis of two successive

frames in single pass resolution and using a 3x3-sized

neighborhood. Assuming to have already completed

the starting frame (t =0)using standard planar syn-

thesis, we explain now how to synthesize a generic

pixel (the dark blue one) inside the following frame

(t =1). At this synthesis stage, the light green part

of the image has already been synthesized, and pro-

ceeding in scan-line order only the neighboring pix-

els above and on the left of the current pixel at posi-

tion (x

) are known. Consequently, the neighbor-

hood - bright blue pixels - is L-shaped. The light grey

part of the image is then generated in the same way in

raster scan order.

In order to incorporate temporal information, we

consider the pixel at the corresponding location

) that belongs to the previous step. That frame

has been entirely synthesized, therefore we can con-

sider the complete squared neighborhood around that

pixel. In this way, we build three-dimensional neigh-

borhoods, which comprise of the L-shaped neighbor-

hood from the current frame t plus the corresponding

squared neighborhood from previous time step (t−1).

The pixels that build the extended neighborhood

have to be adequately taken into consideration: it is

important to note that the preceding temporal frames

contribute to the 3d-neighborhood with different -

non-uniform - weights, as pixels in the current frame

present less correlation with pixels that belong to pre-

vious frames.

Figure 4: Five-sized neighborhood model (L-shaped plus

square-shaped) with two-level multi-resolution synthesis.

This is shown in Figure 4, which describes the tech-

nique for a three-frames process in case of larger sized

neighborhood (size = 5) and with two levels of multi-

resolution image pyramids. From left to right, the

illustrations show the texture evolution in time: the

right-most output slice represents the current frame.

Looking instead from right to left, we go back in

time and the layers inﬂuence to the right most one de-

creases. From bottom (coarse scale) to top (details),

multi-pass synthesis is executed using sub-band trans-

forms.

3.5 Implementation Steps

The algorithm synthesizes all the output pixels of a

single frame, and this for each frame in succession.

A cubic neighborhood N

is build for every output

pixel P

(x, y), with x ∈ [0,W

out

], y ∈ [0,H

out

], be-

ing W

out

and H

out

, respectively, the width and the

height of the output image. A similarity metric, based

on these neighboring pixel values, is computed with

least squares, and used as distance function to mea-

sure pixel similarity. In this way the best matching

pixels can be chosen.

The fundamental steps are:

1. Initialization: set values of output image dimen-

sion, time period, pyramid levels; deﬁne the con-

trolling deformation ﬁeld

2. First step: two-dimensional synthesis (t =0)

3. Further steps: three-dimensional synthesis (t>0)

We use the algorithm of (Taponecco and Alexa, 2004)

for the ﬁrst step of the algorithm. The synthesis steps

for the generation of the frames at general time step

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

288

t>0 are conducted as follows:

• Build a neighborhood N

for every pixel P

(x, y),

including the L neighborhood and further squared

neighborhoods (in number and resolution depend-

ing on the N

size and levels l of the pyramid)

• Evaluate the deformation ﬁeld D at the current out-

put position and time instant, and calculate promi-

nent ﬁeld features (phase, magnitude, curl, ...)

• Use this information to accordingly modify the in-

put sample inﬂuencing its structure and setting the

calculated directions to be the new orientation

• Build all possible N

around P

(i, j) inside the in-

put sample and calculate the similarity metrics

• Compare the entries of the input neighborhoods

array - on the base of distance function - with

(x, y)) and choose the most similar one

• Select that value P

(i, j)|

Max similarity

and set it

to be the current output pixel

• Proceed in scan-line order till the output texture is

completed

• Repeat this procedure for all levels l of image

pyramid and for all following temporal frames t in

the sequence of temporal range τ

Pi , i = Xi + Yi * Wout

Wout

Hout

Tout

T1 (W1 * H1)

T2 (W2 * H2)

j (Wj * Hj)

i (Wi * Hi)

.......

.........................

PN , N = (Wout * Hout)

P1 P5

.......

Tn (Wn * Hn)

T0 (W0 * H0)

Filter

.......

.........................

.......

Filter

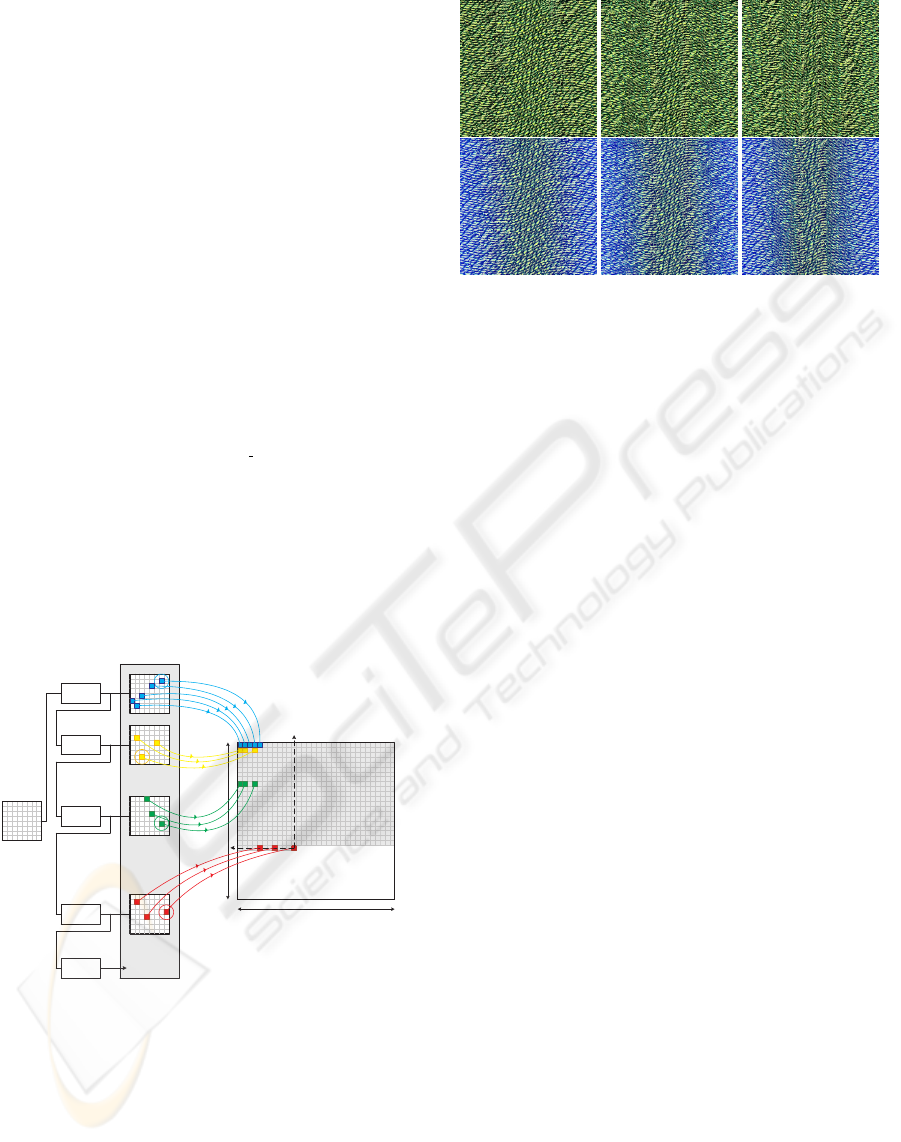
Figure 5: Filters’ bank for sample variation in non-

homogeneous texture synthesis.

3.6 Filtering

As shown in Figure 4, in addition to the use of a de-

formation ﬁeld, textures may be modiﬁed over time in

a progressive way through ﬁltering operators. We in-

tegrated such functionalities in our approach to allow

more manipulation.

Figure 6: A sinusoidal distortion ﬁeld modiﬁes a sample

(top), and a ﬁlter based on a blue component additionally

highlights the ﬁeld intensity in the same frames serie (bot-

tom).

Figure 5 shows one of the possible blocks schemes

for progressive ﬁltering. This operation may be in-

serted in the temporal synthesis scheme to extend its

functionalities (note the ﬁlter blocks in Figure 2).

3.7 Input Seed Processing

The ﬁlters and operators that act over the input texture

example may operate at runtime, at a pre- or at a post-

processing stage.

Some ﬁlters are applied during the synthesis

process to modify the sample seed, as in the case of

the scaling operator, which is responsible of varying

the resolution of the example texture.

Some operators may modify the input texture be-

fore the synthesis starts: for example the rotating op-

erators pre-computes rotated versions of the original

sample, generating an input set to be used as source

during the synthesis.

Some others DSP ﬁlters, as blurring, brightening,

embossing, coloring, may be applied directly on the

synthesized output, as they get - from the synthe-

sis process block - the relevant ﬁeld variables, which

have to be used as parameters to deﬁne the kernel.

4 RESULTS AND DISCUSSION

We have tested our approach in a variety of cases, in

particular for structured textures (Figure 6, 7, 8, 9).

We have mainly used directional samples, since pat-

terns that present accentuated features along a major

axis better exploit movement in the given directions.

Using textures having anisotropic pattern, it is easier

to visualize and enhance the information carried by

the control vector ﬁeld.

LOCAL CONTROL FOR TEMPORAL EVOLUTION OF TEXTURED IMAGES

289

Figure 7: Examples of ﬁltered texture frames sequences. In both cases, four temporal frames extracted from a longer sequence

are shown. They represent the time-varying texture at different time instants.

We believe this approach is promising for many

applications, including the visualization of animated

textures and the texturing of dynamically varying sur-

faces, as it is possible to generate animations of tex-

tures in an automatic and straightforward way. The al-

gorithm does not present any restriction for the choice

of the control ﬁeld expression and of the ﬁltering pa-

rameters. This offers a technique, which is easily

adaptable for a variety of applications.

The values we mostly used to produce the outputs

presented in this paper are 32x32 pixels for the size of

the input samples, and 256x256 and 256x512 for the

generated output. The synthesis time is essentially

comparable to the other pixel-based approaches. The

length of the frames’ sequence can be arbitrary and

animations could in theory be endless. An interesting

example of this is to opportunely design a cyclic con-

trolling function, which can repetitively deform the

pattern without producing artifacts or discontinuities

between different animation cycles.

4.1 Limitations and Optimization

When using texture patterns characterized by having

a complex structure, a large sized neighborhood is re-

quired to allow the synthesis algorithm to learn and

reproduce the sample statistics. In such a case, the

computational complexity rapidly increases. In addi-

tion, the eventual use of time-varying scaling opera-

tors over the input sample also leads to a larger neigh-

borhood size.

An important point to consider is the following: in

a few cases, we noted the occurrence of a sort of ﬂick-

ering effects in the transition between some frames

during the animation. The input sample may occa-

sionally strongly varies (through rotation, scaling and

other operators) between the different time steps: in

such a case, the collection of successive neighbor-

hoods for the best pixel choice could present discon-

tinuity. We solve this problem by considering, for the

neighborhood matching, only samples that we have a

posteriori re-rotated, with respect to the current pixel

as center of the operation. This guaranties better and

smoother results. Occasional spatial or temporal dis-

continuities might occur due to the pattern structure

of the chosen sample and they result from the nature

of the algorithm: in this case they can be removed

in a simple way by using a larger neighborhood or a

higher pyramid levels’ number, or could be blurred

away.

5 APPLICATIONS AND

EXTENSIONS

Image-based scientiﬁc visualization: the presented

texture-based synthesis procedure results to be useful

for the visualization of time-varying vector and ﬂows

ﬁelds. This is similar to the approach in (Taponecco

and Alexa, 2003), which we have here adapted and

extended from the spatial to the spatio-temporal do-

main. With our approach, ﬁeld properties such as

magnitude, phase and direction can be simply visu-

alized in their temporal evolution through the use of

adequate operators over the given input sample.

Non-homogeneous textures: our approach contains

techniques for non-homogeneous texture generation.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

290

Figure 8: A fabric (top) and a directional (bottom) texture are controlled by a vector ﬁeld. Scaling of the sample reﬂects

magnitude information of the ﬁeld; the resolution of the original sample is accordingly adjusted.

Figure 5 shows an example of how ﬁlter banks can

inﬂuence an input sample to generate a sample set (re-

fer to (Taponecco and Alexa, 2004) for more details).

The ﬁlters can be variable in time as well; we insert

the dashed block in the chain of the temporal synthe-

sis process (Figure 2).

Texture ﬂow: besides modelling general and con-

trolled motion, our technique may visualize repeti-

tive stationary motion, similarly to the approaches de-

scribed in § 2.1. Using directional samples, it is possi-

ble to generate an animated ﬂow of the texture’s struc-

ture along the pattern’s major direction.

Texture mixture and metamorphosis: Mixture and

metamorphosis in textures has recently become very

popular (see for instance (Zhang et al., 2003)). Our

methodology can contribute to produce interesting

texture transformations over time. Part of our future

work is to combine it with those techniques.

6 CONCLUSION

This paper outlines a technique for the synthesis of

varying textures. We propose a novel methodol-

ogy for the generation of continuous texture anima-

tions and, as speciﬁc case, smooth time-varying and

texture-based ﬁelds visualization. Interesting applica-

tions include decoration of surfaces that are deformed

or in motion such as cloths or other materials; textures

are a valid solution in helping shape and material per-

ception, and local control in their generation and vari-

ation is fundamental to augment such features.

Our algorithm is based on a recursive synthesis pro-

cedure that uses a three-dimensional neighborhood

model. The method is simple and general, but also

ﬂexible and capable of generating a variety of effects.

User intervention is offered: it is possible to pro-

duce speciﬁc output sequences through easy and in-

tuitive control parameters and formulæ. The synthe-

sized output frames conserve appearance and struc-

tural properties similar to the input sample. They are

controlled through a speciﬁed vector ﬁeld: they have

to be adapted locally to follow speciﬁed directions,

and accordingly vary their structure and attribute in

a non-homogeneous way. Resolution of the original

texture pattern, as well as color or shading attributes

can be easily varied. This synthesis procedure, being

pixel-based, does not run at interactive rates. The ad-

vantages, on the other hand, include the smoothness

of the outputs, and the presence of extra degrees of

freedom in the texture synthesis process, as local con-

trol has effect over individual pixels. In conclusion,

the main contribution of this work is to offer a general

and intuitive technique to synthesize variable textures

and animate them. These frames’ animation can de-

scribe a broad variety of temporal pattern variation.

Furthermore, this methodology is also a straightfor-

ward solution for the visualization of unsteady vector

ﬁelds, which is usually still challenging and calcula-

tion intensive.

REFERENCES

Bar-Joseph, Z., El-Yaniv, R., Lischinski, D., and Werman,

M. (2001). Texture mixing and texture movie synthe-

sis using statistical learning. In IEEE Transactions on

LOCAL CONTROL FOR TEMPORAL EVOLUTION OF TEXTURED IMAGES

291

Figure 9: Example of a varying bricks-like texture pattern.

Visualization and Computer Graphics, volume 7(2),

pages 120–135. IEEE Computer Society.

Bonet, J. S. D. (1997). Multiresolution sampling procedure

for analysis and synthesis of texture images. In Com-

puter Graphics, pages 361–368. ACM SIGGRAPH.

Dischler, J.-M., Maritaud, K., Levy*, B., and Ghazanfar-

pour, G. (2002). Texture particles. Computer Graph-

ics Forum, 21(3):401–401.

Doretto, G., Jones, E., and Soatto, S. (may 2004). Spa-

tially homogeneous dynamic textures. In Proceedings

of ECCV ’04, Prague, Czech Republic.

Efros, A. and Leung, T. (1999). Texture synthesis by non-

parametric sampling. In International Conference on

Computer Vision, pages 1033–1038.

Fitzgibbon, A. W. (july, 2001). Stochastic rigidity: Image

registration for nowhere-static scenes. In Proceed-

ings of International Conference on Computer Vision

ICCV ’01, pages 662–670, Vancouver, BC, Canada.

Heeger, D. J. and Bergen, J. R. (1995). Pyramid-Based

texture analysis/synthesis. In Cook, R., editor, SIG-

GRAPH 95 Conference Proceedings, Annual Confer-

ence Series, pages 229–238. ACM SIGGRAPH. held

in Los Angeles, California, 06-11 August 1995.

Julesz, B. (1962). Visual pattern discrimination. In IRE

Transaction on Information Theory, volume IT-8.

Julesz, B. (1981). Textons, the elements of texture percep-

tion and their interactions. In Nature, volume 290,

pages 91–97.

Kwatra, V., Essa, I., Bobick, A., and Kwatra, N. (2005).

Texture optimization for example-based synthesis. In

ACM Transactions on Graphics, SIGGRAPH.

Lefebvre, S. and Hoppe, H. (2005). Parallel controllable

texture synthesis. In ACM Transactions on Graphics,

SIGGRAPH.

Li, Y., Wang, T., and Shum, H.-Y. (2002). Motion texture:

A two-level statistical model for character motion syn-

thesis. In Hughes, J., editor, SIGGRAPH 2002 Confer-

ence Proceedings, Annual Conference Series, pages

465–471. ACM Press.

Portilla, J. and Simoncelli, E. P. (1999). Texture modelling

and synthesis using joint statistics of complex wavelet

coefﬁcients. In IEEE Workshop on Statistical and

Computational Theories of Vision.

Pullen, K. and Bregler, C. (july, 2002). Motion capture

assisted animation: Texturing and synthesis. In Pro-

ceedings of SIGGRAPH 2002. ACMPress.

Schoedl, A., Szeliski, R., Salesin, D. H., and Essa, I. (july,

2000). Video textures. In Proceedings of SIGGRAPH

2000, pages 489–498. ACMPress.

Soatto, S., Doretto, G., and Wu, Y. N. (july, 2001). Dynamic

textures. In Proceedings of ICCV ’01, Vancouver, BC,

Canada.

Szummer, M. and Picard, R. W. (1996). Temporal texture

modeling. Technical report.

Taponecco, F. and Alexa, M. (2003). Vector ﬁeld visualiza-

tion using markov random ﬁeld texture synthesis. In

IEEE TCVC Visualization Symposium. ACMPress.

Taponecco, F. and Alexa, M. (2004). Steerable texture syn-

thesis. In Eurographics 2004, pages 57–60, Grenoble,

France. ACMPress.

Wei, L. and Levoy, M. (2000). Fast texture synthesis using

Tree-Structured vector quantization. In Hoffmeyer, S.,

editor, Proceedings of the Computer Graphics Con-

ference 2000 (SIGGRAPH-00), pages 479–488, New

York.

Zhang, J., Zhou, K., Velho, L., Guo, B., and Shum, H.-Y.

(2003). Synthesis of progressively variant textures on

arbitrary surfaces. ACM Transactions on Graphics,

22(3):295–302.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

292