
SURFACE CONSTRUCTION USING TRICOLOR
MARCHING CUBES
Shaojun Liu, Jia Li
Oakland University
Rochester, MI 48309, USA
Xiaojun Jing
Beijing University of Posts and Telecommunications
No. 10 Xi Tu Cheng Rd, Beijing 100876, China
K
eywords:
Marching cubes, 3D surface construction.
Abstract:
This paper presents a generalized marching cubes (MC) method for 3D surface construction. Existing MC
methods require the sample values at cell vertices to be different from the threshold or modify them otherwise.
The modification may introduce topological changes to the constructed surface. The proposed Tricolor MC
method allows cell vertices with sample values which equal the threshold to lie on the surface. It constructs the
surface patches by exhausting the Eulerian circuits in the cells without changing sample values. The simulation
results show that the TMC method better preserves the topology of the surfaces that pass through cell vertices
and gives good results in other general cases.
1 INTRODUCTION
Three dimensional (3D) surface construction is a
widely studied topic in computer graphics and com-
puter vision. Polygonal representation of 3D surface,
or mesh, is extensively used in rendering on graph-
ics hardware, texture mapping, and shape analysis.
The marching cubes (MC) method is the most pop-
ular method to generate isosurface on volumetric data
at uniform grids. Proposed by Lorensen and Cline in
1987, MC method is fast in extracting high resolu-
tion isosurfaces and simple to implement (Lorensen
and Cline, 1987). However, the original MC method
has problems such as topology inconsistency and rep-
resentation inaccuracy. Since then a variety of MC
methods have been proposed for improvements.
Nielson and Hamann proposed an asymptotic de-
cider to solve the face ambiguity which happens in
a cube face with two diagonally opposite vertices
marked positive and the other two marked nega-
tive (Nielson and Hamann, 1991). Chernyaev used
33 configurations to eliminate the internal ambigu-
ity which occurs in the interior of a cube (Chernyaev,
1995). Ho et al. proposed CMS method to preserve
sharp features (Ho et al., 2005).
One of the original MC assumptions is not ad-
dressed by later variations, which assumes the cell
vertices lie either inside or outside the surface, not
on the surface. It meets a problem when isocontours
such as level set pass through cell vertices. To elide
this problem, existing MC methods modify the sam-
ple values that equal threshold. This modification,
however, may introduce obvious topological changes
in some cases as shown in the latter part of the paper.
This paper proposes a more general MC method
that does not modify the sample values. It constructs
surface by finding Eulerian circuits in the cell. The
paper is organized as following. In Section 2, the
background for MC method is briefly introduced. In
Section 3, we propose the new MC method and intro-
duce the surface construction procedure. The exper-
imental results are presented in Section 4. Section 5
concludes the paper.
2 BACKGROUND
The output of the marching cube algorithm is a mesh
representing the 3D surface. A mesh M is a pair
(K, V ), where K is a simplicial complex represent-
ing the connectivity of the vertices, edges and faces,
thus determining the topological type of the mesh, and
V = {v
1
,...,v
m
},v
i
∈
3
is a set of vertex coordi-
nates defining the shape of the mesh in
3
.
The input of the MC algorithm is volumetric data,
which has sample value associated with each grid
point. The samples at cell vertices are thresholded
before isosurface extraction. Hereafter the sample
319
Liu S., Li J. and Jing X. (2006).
SURFACE CONSTRUCTION USING TRICOLOR MARCHING CUBES.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 319-324
DOI: 10.5220/0001350703190324
Copyright
c
SciTePress

−
(a) (b) (d)(c)
0
0
+
+
0
0
0
+
++
+
+
+
0
+
+
+
0
−
−
+
−
−
−
−−
−
−−
−
−
Figure 1: Topological changes caused by sample value
modification. In each subfigure, the figure on the top shows
the original sample values, while the figure at the bottom
shows the possible topological change.
value is referred as that minus threshold. And we
call the cell vertex with positive/negative/zero sam-
ple value positive/negative/zero cell vertex re-
spectively. Existing MC methods do not allow cell
vertices lie on the surface, or zero cell vertices. Un-
der this assumption, the surface is limited to intercept
the cell in 2
8
= 256 ways since each of the eight
cell vertices can lie either inside or outside the sur-
face. It is equivalent to coloring the eight cell vertices
with two colors. Hence we call existing MC methods
bicolor methods. By exploiting the symmetries in the
256 ways, Lorensen et al. summarized the cases into
15 patterns in the original MC method (Lorensen and
Cline, 1987).
To hold this assumption, existing bicolor MC meth-
ods have to modify the zero sample value in prac-
tice. For example, as level set may pass through grid
points, Han et al. change the sample value at such grid
points from zero to negative (Han et al., 2003). This
kind of modification may introduce obvious topolog-
ical changes, which is shown in Fig. 1. The thick line
in the figure represents the interception of surface and
cell face. Modification on sample value changes the
original cell face into ambiguous faces as shown in
(a) and (b). And the interceptions become completely
different after modifications on (c) and (d). Secondly,
the isosurface extracted should be neutral with posi-
tive and negative data samples. In other words, the
isosurface should not change if we multiply the sam-
ple data with −1. Modifying the sample value, how-
ever, can lead to two different topological results for
the same set of data as shown in the experiment sec-
tion of this paper. Thirdly, modifying sample value
may introduce nonexistent face as shown in the ex-
periments.
This defect is regarded as a technical problem in
(Gelder and Wilhelms, 1994), and one of the several
major artifacts in most existing isocontour software
(Han et al., 2003). One of the reasons that existing
bicolor MC methods elide this problem is too many
cases are introduced without this assumption. If the
sample at cell vertex is allowed to be zero, each of the
eight cell vertices has three instead of two possible
positions relative to the surface, i.e. inside, outside
(1) (2) (3)
(4) (5) (6)
Figure 2: An example of one possible way to find 4 patches
edge by edge in a cell with 12 vertices.
or on the surface. Thus the surface intercepts the unit
cube in a total of 3
8
= 6561 ways. It is equivalent to
coloring cell vertices with three colors. We name our
method tricolor MC (TMC) to reflect this character.
To enumerate all these ways and reduce the symme-
tries manually, as what has been done in (Lorensen
and Cline, 1987), is extremely tedious and error-prone
to human. In the following sections, we will eliminate
this assumption to include zero cell vertices without
modification.
3 SURFACE CONSTRUCTION
For the convenience of discussion, we define patch
as the close interception of the isosurface and a cell, a
polygon formed by connecting the surface mesh ver-
tices. A patch edge is the interception of the surface
with a cell face, whose end points are two adjacent
surface mesh vertices on the cell edge. The degree
of surface vertex is the number of patch edges inci-
dent on the vertex. Since we are only interested on the
patch edges in one cell, hereafter the vertex degree ac-
tually refers to the degree in one cell. As mentioned
in Section 2, the cell may hold the patches in 6561
ways if taking zero cell vertices into consideration.
Instead of enumerating all these cases, we go back to
two dimensions to examine the ways of the intercep-
tion of isosurface and one cell face, or the patch edges.
As the patch is enclosed by patch edges, it forms an
Eulerian circuit, a graph cycle which uses each graph
edge exactly once. It suggests finding the patches in
the cell by finding the Eulerian circuits. We start from
any of the surface vertex, find one patch edge incident
on it if possible, and continue with the surface vertex
that is the other endpoint of the patch edge until we
return to the original vertex. After one Eulerian cir-
cuit, or a patch, is completed, repeat the process until
all the patch edges in the cell have been visited. Then
we find all the patches in the cell. An example of one
possible way to find 4 patches edge by edge by within
one cell is illustrated in Fig. 2.
As more than two surface vertices may lie on a
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
320
(13)
++
++
(1)
++
+−
(3)
++
0−
(5)
++
−−
(6)
++
00
(4)
0+
0+
0+
00
(7) (8)
++
+0
(2)
(9)
0
+
0
−0
(11)(10)
0+
−
0+
−+ 00
(12)
00
−
+
−
+
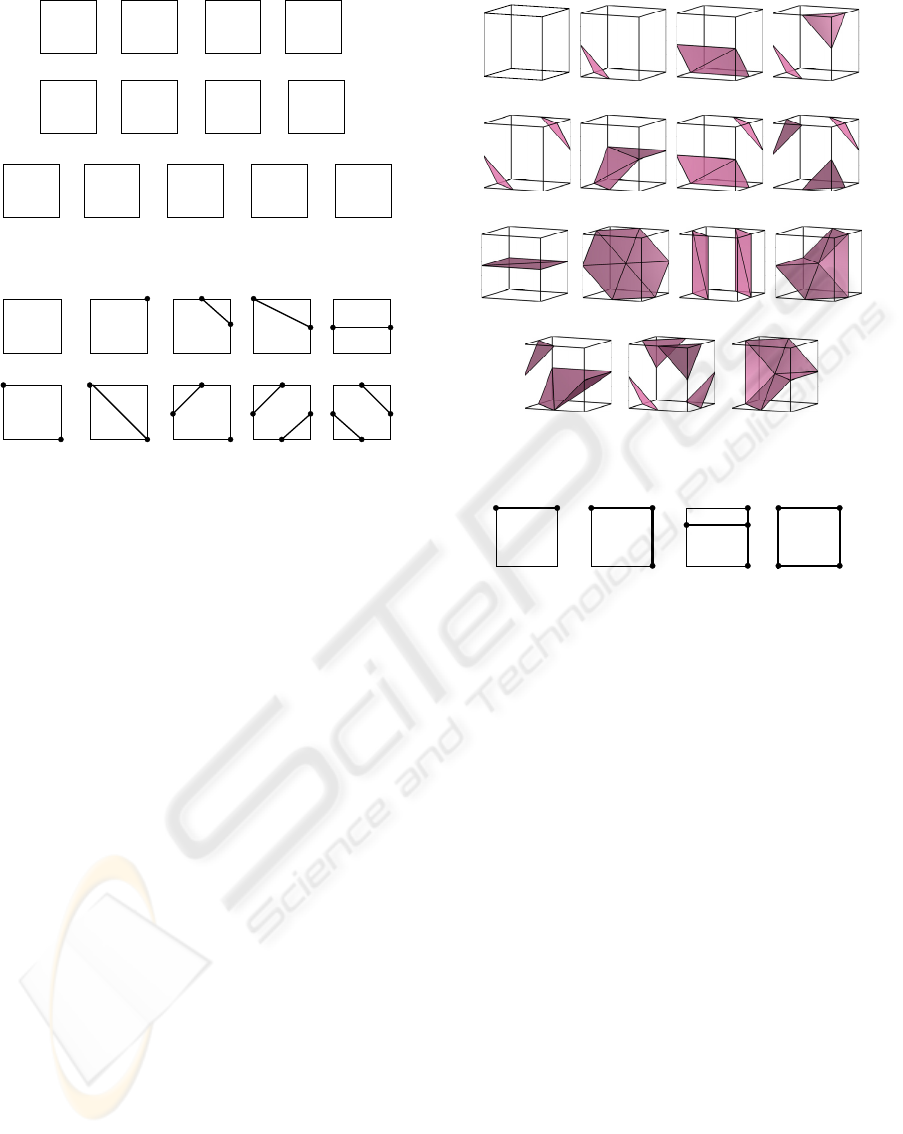
Figure 3: 13 cases of squares with zero cell vertices.
(9)
++
0−
(5)
+
+
++
++
+0
(1) (2)
+
+
(3)
+
−
+
+
−−
(6)
0
+
0
+
(7) (10)
0+
+−
(13.a)
−+
−+
(13.b)
−
+
−
+
0+
0−
Figure 4: 10 cases out of the original 13 cases in Fig. 3 with
zero cell vertices and their corresponding patch edges.
cell face, there are multiple ways to define the patch
edges. And the resulted patches in the cell would be
completely different. So we need to count how many
ways to define the edges on a cell face and make our
choice. Banks et al. counted the cases to produce
substitopes in the MC method (Banks and Linton,
2003). They enumerated 13 distinct cases in two di-
mensions with zero cell vertices as shown in Fig 3, in
which symmetries between positive and negative cell
vertices have been eliminated. Many of these cases,
however, allow ambiguous ways to connect the patch
edges. Various methods have been proposed to solve
the ambiguities. The bilinear interpolation over the
cell face is adopted to solve the ambiguity problem in
our study,
φ(u, v)=φ
00
(1 − u)(1 − v)+φ
01
(1 − u)v
+φ
10
u(1 − v)+φ
11
uv
(1)
where φ(u, v) stands for the value at logical coordi-
nates (u, v) on the cell face (Nielson and Hamann,
1991). This bilinear interpolation solves most cases
as shown in Fig. 4. The choice of ambiguous sub-
cases 13.a and 13.b is made according to the method
proposed in (Nielson and Hamann, 1991). Note that
the proposed method does not address internal ambi-
guity since it only allows patch edges on the cell face.
Case 1, 3, 6, 13.a and 13.b of Fig. 4 correspond
to all the 15 cases in the original MC method. To
show that the proposed method cover all the cases
of the original MC methods, we use the 15 cases in
the original MC method as input of TMC method and
get the same patches as the original MC method in
Fig. 5, though the triangulation is different. TMC
(0) (1) (2) (3)
(4) (5) (6) (7)
(8) (9) (10) (11)
(12) (13) (14)
Figure 5: 15 cases in original MC method covered by TMC.
+
0
(11)
0+
−00
(12)
0
0
+
00
(4)
0+
00
(8)
Figure 6: Bilinear Interpolation of case 4, 8, 11 and 12 in
Fig. 3.
method also generates the same results for all the pos-
sible configurations with ambiguous faces as those in
(Nielson and Hamann, 1991). Due to page limit, we
do not list the result here.
However, ambiguities in case 4, 8, 11 and 12 of Fig.
3 are not solved well by bilinear interpolation, which
is shown in Fig. 6. In case 11, one patch edge inter-
cepts with the other between its endpoints, resulting
in discontinuous surface. And too little information
is available to decide the patch edges at the border of
a cell face, which is called border edge. To ensure
the patch edge is on the border of two regions with
different sign, both cell faces incident on the possible
border edge need to be checked. The cases in Fig.
4 can be used to solve these ambiguities if the two
adjacent cell faces are ”merged” into one. In the fol-
lowing, we enumerate the combinations of case 4, 8,
11 and 12 with the 13 cases of Fig. 3.
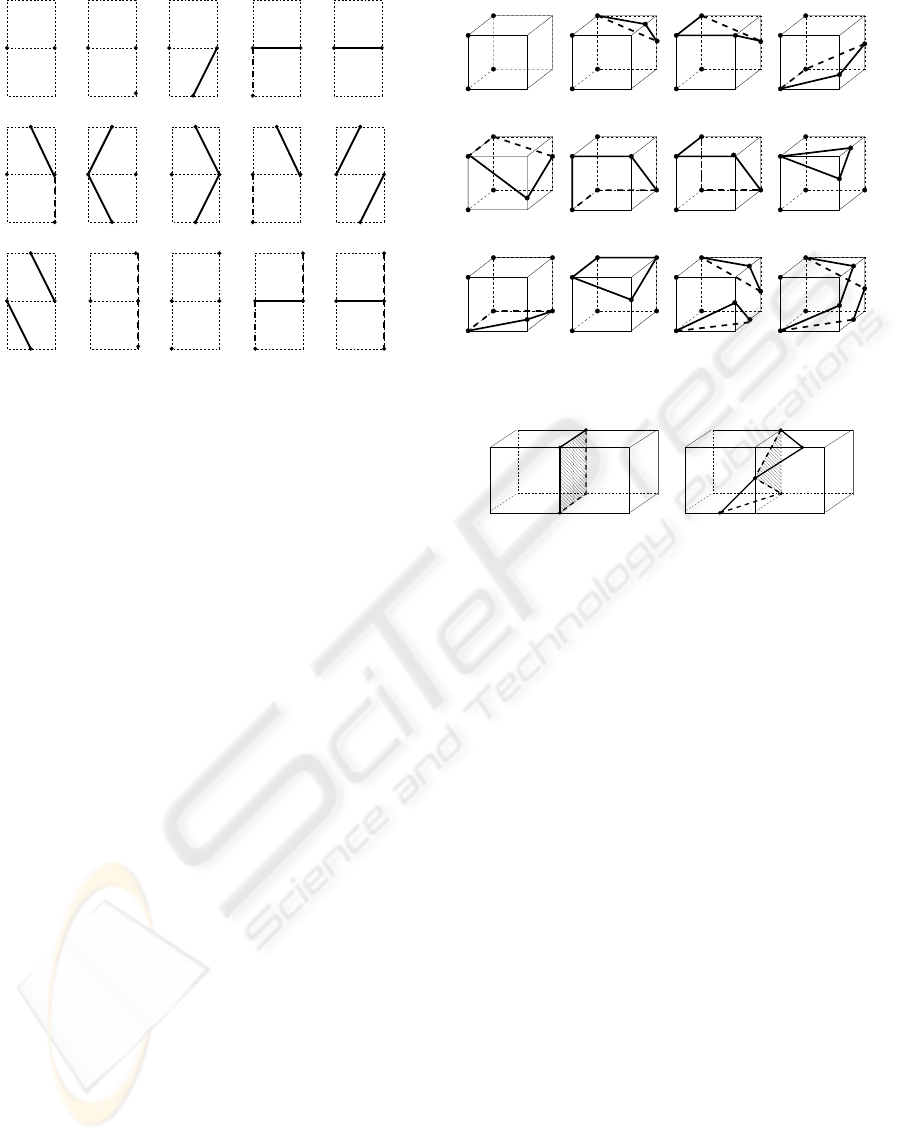
First we list the combinations without case 12 as
shown in Fig. 7. For example, case 4 of Fig. 3 has
five sub-cases from 4.a to 4.e in Fig. 7 with regard
to the cell face incident on the possible border edge.
And the ambiguous sub-cases 11.e.1 and 11.e.2 are
solved in the same way as 13.a and 13.b of Fig. 4. As
for the sub-cases 11.c.1 and 11.c.2, we choose 11.c.1
if the sum of absolute sample values at positive cell
vertices is greater than that at negative cell vertices,
SURFACE CONSTRUCTION USING TRICOLOR MARCHING CUBES
321
(8.h)
00
+0
−0
0
0
+
0
0
−
00
+
+
0
0
00
+
+
0
0
0
0
+
+
−
−
0
0
+
+
−
0
00
+
+
−
−
(11.b,8.c) (11.c.1)
00
+
+
−
−
00
+
+
−
0
(11.c.2) (11.d,8.d)
0
0
+
+
−
−
00
++
+0
0
0
++
+
+
(4.a)
00
++
+−
(4.b,8.a) (4.c,11.a)
00
++
0−
0
0
++
−
−
(4.d,8.b) (4.e)
(11.e.1)
(8.e) (8.f)(11.e.2) (8.g)
Figure 7: Solving ambiguities in case 4, 8 and 11 of Fig. 3.
Solid line stands for the patch edge while dotted line for the
undecided patch edge.
and 11.c.2 otherwise. As each of the sub-cases of case
8 in Fig. 7 has two possible border edges, we need to
check the two adjacent cell faces incident on the two
possible border edges.
As for the combinations with case 12 of Fig. 3, the
other eight cell vertices in the cell have only 13 dis-
tinct configurations of Fig. 3 due to symmetry. So
we can enumerate all the 13 configurations and gen-
erate patch edges accordingly. To use the results in
Fig. 7, we ”shrink” the cell face of case 12 into a bor-
der edge. Fig. 8 shows the patch edges for the twelve
sub-cases of case 12 of Fig. 3 in 3D. Note sub-case
12.a represents the configurations in which the other
eight vertices in the cell are the cases of 1, 2, 4, 7, 8 or
12 of Fig. 3. As for the ambiguous sub-cases 12.d.1
and 12.d.2, 12.e.1 and 12.e.2 or 12.g.1 and 12.g.2,
we choose 12.d.1, 12.e.1 or 12.g.1 if the sum of ab-
solute sample value at positive cell vertices is greater
than that at negative cell vertices, and 12.d.2, 12.e.2
or 12.g.2 otherwise. And the ambiguous sub-cases
12.h.1 and 12.h.2 are solved in the same way as 13.a
and 13.b in Fig. 4.
By solving the 13 tricolor cases of Fig. 3 accord-
ing to Fig. 4, Fig. 7 and Fig. 8, we can decide patch
edges for all the 6561 cases in 3D. But we still need
to ensure that TMC method can find all the patches by
searching the Eulerian circuits in the cell. The condi-
tion of Eulerian circuits is no surface vertex with odd
degree. We show briefly in the following that the de-
gree of surface vertex in one cell is either zero or two.
And the surface vertex with zero degree is isolated
and simply ignored.
Firstly, it is easy to verify the degree of surface ver-
tex, which is not zero cell vertex, is two. And the de-
gree of surface vertex in Fig. 8 is either zero or two.
Secondly, we show that the degree of surface vertex
−
(12.a)
0
0
0
0
0/+
0/+
0/+
0
0
0
0
−
−
(12.d.2)
+
0
0
0
00
−
(12.g.1)
+
0
0/+
+
(12.b)
0
0
0
0
+
−
+
0
0
0
0
0
(12.e.1)
+
0
−
0
0
0
00
(12.g.2)
+
0
−
+
(12.c)
0
0
0
0
+
+
0
−
0
0
0
0
(12.e.2)
+
0
0
−
0
0
0
0
−
+
(12.h.1)
+
−
(12.d.1)
0
0
0
0
+
−
−
+
0
0
0
0
(12.f)
+
0
+
−
0
0
0
0
−
+
(12.h.2)
+
Figure 8: Solving ambiguities in case 12 of Fig. 3.
−
0
0
0
0+
+
+
+
−
−
−
(a) Case 12 of Fig. 3
0
0+
+
+
+
−
−
−
−
+
−
(b) Case 11 of Fig. 3
Figure 9: Insert one patch between two adjacent cells rep-
resented by the filled region.
is at most two for the cases with zero cell vertices in
Fig. 4 and Fig. 7. In Fig. 4, if one zero cell ver-
tex connects to three patch edges like case 5 or 9, it
will cause a contradiction, in which the cell vertices at
the two sides of one patch edge are of the same sign.
In Fig. 7, we only need to check the degree of zero
cell vertex that possibly connect more than one patch
edge. Since only two cell vertices are not known in
Fig. 7, we get the degree is two by enumerating the
nine combinations of the two unknown cell vertices
in sub-cases 4.d, 11.b, 11.c.1, 11.c.2, 8.e, 8.g and 8.h.
Finally we show that the degree of zero cell vertex is
not one. We only need to check the zero cell vertex
that connects only one patch edge in Fig. 4 and Fig.
7. From case 5 and 9 of Fig. 4, the zero cell ver-
tex connects to only one patch edge on one cell face
if its two adjacent cell vertices are of different sign.
Similarly it connects to at least one patch edge in its
other adjacent cell faces, if its third adjacent cell ver-
tex (not displayed) is positive or negative. If its third
adjacent cell vertex is zero, only two other unknown
cell vertices (not displayed) affect its degree. We get
the degree is two by enumerating the nine combina-
tions of the two unknown cell vertices. In Fig. 7, the
degree of zero cell vertex in sub-cases 4.c, 4.e, 11.e.1,
11.e.2 is two since its two adjacent cell vertices are of
different sign. And we get the degree is two by enu-
merating sub-case 4.d, 11.b, 11.d, 8.e, 8.g and 8.h.
As the cell face of case 12 of Fig. 3 is shared by
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
322

−
+
+
−−
−
−
−−
−
0
+
0
+
−
−
++
+
+
+
(a) Original Topology (b) TMC (c) Bicolor MC
Figure 10: Topologies comparison between TMC and the
Lewiner’s MC implementation on cases 2 in Fig. 4.
two adjacent cells, if it separates two regions of dif-
ferent sign, we need to insert a patch between the two
adjacent cells as shown in Fig. 9(a). Moreover, as
the cell face of case 11 may result in different patch
edges in two adjacent cells, a new patch is also needed
as shown in Fig. 9(b). Note these patches inserted
between adjacent cells do not affect the previous con-
clusion about the vertex degree in the cell.
The orientation of patch vertices is adjusted to keep
the patch normal pointing outward the surface consis-
tently. Once all the patches are found, we complete
the whole front surface. To get the triangulate mesh,
we triangulate each patch by using one vertex as the
common triangle vertex. To avoid self intersection be-
tween patches within one cell (Gelder and Wilhelms,
1994), we add a new vertex, which is the average of
other vertices, as the common triangle vertex for poly-
gons with more than five edges.
Banks and Linton also counted the tricolor cases
in three dimensions in MC method by numerical al-
gorithms (Banks and Linton, 2003). They found 147
cases out of the original 6561 cases. However, it is
unrealistic to verify this result by hand. Enumerating
all the ambiguous cases for these 147 cases is also a
tedious task.
Another advantage of the TMC method is that 2D
contours have already been generated by patch edges
within each patch. By collecting the patch edges on
every plane, we can get the 2D contour at specified
position. Ho et al. also constructed surface by finding
2D segments in their CMS method (Ho et al., 2005).
But the CMS method does not consider the zero cell
vertex, hence it inherits the topological artifacts of the
bicolor algorithms.
4 EXPERIMENTAL RESULTS
AND ANALYSIS
To show the advantage of the proposed TMC method,
we test it over the cases shown in Fig. 10 and com-
−
0
00
0
−
−
−
−
−
−−
0
++
++
+
+
++
0
00
(a) Original Topology (b) TMC (c) Bicolor MC
Figure 11: Topologies comparison between TMC and the
Lewiner’s MC implementation on case 12 in Fig. 3.
(a) Two torus (b) Case (c) Blooby
Figure 12: Examples constructed by TMC.
pare it with an existing bicolor MC method imple-
mented by Lewiner et al. (Lewiner et al., 2003).
Lewiner’s implementation is based on Chernyaev’s
technique, to solve the ambiguity problem on the cell
face (Chernyaev, 1995). It modifies the zero sample
value at cell vertex to a small positive value. For the
case shown in top row in Fig. 10, Lewiner’s method
reports eight times of case 2 of Fig. 5 and gener-
ates 16 triangles. When the data are multiplied by
−1 as shown in the bottom case in Fig. 10, the pro-
posed TMC method consistently preserves the orig-
inal topology, while Lewiner’s method reports eight
times of case 1 of Fig. 5 and generates 8 triangles. To
illustrate, we enlarge its small positive value to 0.05
and get the result in Fig. 10. Note this enlargement
does not change its topology or the number of trian-
gles generated.
On case 12 of Fig. 3, Lewiner’s MC implementa-
tion outputs two planes for the top case in Fig. 11.
But it generates no plane when the data samples are
multiplied by −1 as the bottom case in Fig. 11. In
comparison, TMC gives no plane consistently since
these zero cell vertices are not the boundary of two
regions with different signs.
To illustrate TMC can extract the isosurface cor-
rectly, we synthesize volume data with known under-
lying functions and use them as the input (Lewiner
et al., 2003). The results are accordant with the un-
derlying functions as shown in Fig. 12. We also
test the proposed algorithm on volumetric data with
unknown underlying surface function. A series of
CT lung scans have been downloaded from the Na-
SURFACE CONSTRUCTION USING TRICOLOR MARCHING CUBES
323

(a) 3D surface
(b) 2D contour
Figure 13: Internal lung structures constructed from seg-
mentation results.
tional Cancer Institute [LIDC]. First the 3D image in
the region of interest (ROI) is segmented by level set
method. Then TMC is used to construct surface from
the level set results. Fig. 13(a) shows the results on
the ROI with 290×380×62 voxels. As mentioned, the
2D contours can be conveniently collected during ex-
tracting isosurface by TMC method as shown in Fig.
13(b), while tremendous efforts are needed for gener-
ating 2D contours in most existing MC methods. In
the image, the thin structures like lung bronchia and
fine surface details are well captured. And the results
have been validated by experienced physicians.
We also compare the running time of TMC method
with Lewiner’s MC implementation as shown in Table
1. TMC method is a little bit slower than Lewiner’s
method because of the added cases. It is still a fast
algorithm, which can generate 4 million triangles in
8.5 seconds in one experiment. The table shows that
the number of zero cell vertices are about 1% to 4% of
that of the resulted triangles. All the experiments are
carried out on a Pentium IV 3.2GHZ processor with
1G RAM.
5 CONCLUSION
We propose a tricolor marching cubes (MC) method
for 3D surface construction. Existing bicolor MC
methods do not allow cell vertices whose sample val-
ues equal threshold, or zero cell vertices. Modifying
sample value at such vertices may change the topol-
ogy of original surface. The proposed TMC method
allows the third ”color”, i.e. zero value prevail cell
vertices after thresholding. It constructs the isosur-
face by finding Eulerian circuits in the cells. Com-
paring with the existing MC methods, the proposed
method has the following advantages. First it best pre-
serves the original topology since it does not modify
sample values at cell vertices. Secondly it avoids enu-
merating a large number of the cases introduced by
zero cell vertices. Thirdly it generates 2D contours
of the surface automatically. Simulation results show
that TMC method preserves topology better than ex-
isting MC methods on contacting surfaces and is an
efficient method in constructing 3D surfaces.
Table 1: Running time of TMC and MC method.
Dimension Zero
Cell
Vertices
Triangles Time
(s)
MC
200 × 360 × 28 7407
260545 0.469
TMC 267167 0.718
MC
290 × 380 × 62 22081
548321 1.375
TMC 546660 1.75
MC
512 × 512 × 28 16054
1118504 2.063
TMC 1137072 2.578
MC
512 × 512 × 59 49227
4130056 5.0
TMC 4180029 8.469
REFERENCES
Banks, D. C. and Linton, S. (2003). Counting cases in
marching cubes: Toward a generic algorithm for pro-
ducing substitopes. In IEEE Visualization 2003, pages
51–58.
Chernyaev, E. V. (1995). Marching cubes 33: Construction
of topologically correct isosurfaces. Technical Report
CN/95-17, CERN, Geneva, Switzerland.
Gelder, A. V. and Wilhelms, J. (1994). Topological consid-
erations in isosurface generation. ACM Transactions
on Graphics, 13(4):337–375.
Han, X., Xu, C., and Prince, J. (June 2003). A topology
preserving level set method for geometric deformable
models. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 25(6):755–768.
Ho, C.-C., Lee, P.-L., Chuang, Y.-Y., Chen, B.-Y., and
Ouhyoung, M. (2005). Cubical marching squares:
Adaptive feature preserving surface extraction from
volume data. In EUROGRAPHICS, volume 24.
Lewiner, T., Lopes, H., Vieira, A. W., and Tavares, G.
(2003). Efficient implementation of marching cubes’
cases with topological guarantees. Journal of Graph-
ics Tools, 8(2):1–15.
Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:
A high-resolution 3D surface construction algorithm.
In Proceedings of the 14th annual conference on com-
puter graphics and interactive techniques, pages 163–
169.
Nielson, G. M. and Hamann, B. (1991). The asymptotic
decider: Resolving the ambiguity in marching cubes.
In Proceedings of Visualization ’91, pages 29–38.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
324
