A GEOMETRIC REPRESENTATION FOR THE REAL-TIME

SIMULATION OF NC MACHINING PROCESSES

Aitor Moreno, Carlos Toro, Iosu Arizkuren, Alvaro Segura, Jorge Posada

VICOMTech Association, Paseo Mikeletegi 57, 20009 San Sebastian, Spain

Marcelino Novo

FAGOR AUTOMATION S. Coop. Bº San Andrés, 19 - Apdo.144 - 20500 Mondragón, Spain

Juanjo Falcón

SOME Sistemas Informáticos S.L. Avda. Navarra s/n (oficina 10). 20500 Mondragón, Spain

Nieves Alcaín

Alecop, S. Coop. Loramendi, 11, Apto. 81 - 20500 Mondragón, Spain

Keywords: NC-Machining, Verification, Material Removal, Solid Representation, Simulator, Interactive Rendering.

Abstract: In this paper we present a level-based representation used in the implementation of a real-time material

removal simulator, whose principal feature is to be embedded into a commercial NC machine where the

hardware capabilities are limited. The representation and its supporting architecture is used for the

generation of an interactive simulation of the actual machined part taking as input the NC machine feedback

with the following features: i) The virtual and real simulations must be synchronized, ii) the internal

representation of the objects must be as exact and accurate as possible and iii) the graphical quality should

be acceptable, even with low graphics hardware resources. The mentioned representation was implemented

in the frame of a research project, allowing the evaluation of the architecture with some results presented in

this paper. The results confirm the hypothesis that the current implementation simulates low and medium

complexity models synchronously. More complex models require some tuning of the simulation parameters

in order to be correctly simulated.

1 INTRODUCTION

One of the principal industries to experiment the

advantages of the new computer revolution is the

machine tool workshop. New techniques, control

systems and computerized aids are used by leading

CNC companies to embed more information to the

user and in the meantime to foresee potential

mistakes or even dangerous operations as the pieces

manufactured are in most cases sharp steel objects

that must be handled with extreme caution.

The user nowadays is able to simulate the CNC

program with an outstanding efficiency, resembling

real behaviors with no material waste at all. The

possibility to try different approaches to a piece

manufacture is very interesting as well.

However, for the developer of the CNC system, a

good graphical output (3D real-time representation

of the manufactured object) constitutes a very

expensive development as their principal focus is the

hardware.

Almost every company buys a 3D representation

kernel and provides the simulation and real-time

manufacturing operation as a separate add-on to the

machine.

The 3D kernel used in the simulation of the

manufactured object, provides a set of functions and

possibilities that allows the CNC machine developer

357

Moreno A., Toro C., Arizkuren I., Segura A., Posada J., Novo M., Falcón J. and Alcaín N. (2006).

A GEOMETRIC REPRESENTATION FOR THE REAL-TIME SIMULATION OF NC MACHINING PROCESSES.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 357-363

DOI: 10.5220/0001351503570363

 SciTePress

to show a simulation or real-time action in the CNC

machine workshop.

However, 3D kernels are expensive and only

accessible through a very closed interface which in

many cases is not powerful enough to show the

machine’s potential.

In the scope of the SIMUMEK research project

(Moreno, 2004), we have worked together with a

CNC producer and a NC simulation software

company to test different simulation approaches in a

general framework. The main result of the project is

a low cost NC simulation kernel capable to deal with

different types of machine operations like multi axis

milling, classical lathe (2 ½ DOF) and C-axis lathe.

The obtained simulation kernel is generic and has

been tested with several simultaneous cutters.

In this paper we will address directly the results

obtained from this research project where the most

critical restrictions are:

• There is no previous knowledge of the CNC

machine code.

• The NC machine gives the tool movements as

tool positions, sampled every few milliseconds.

• The graphical system must run in real-time

while the real machine is performing the piece

cut.

This paper will be presented ad follows:

In chapter 2 a brief state of the art is reviewed

not intending to be an extensive study of the actual

techniques but to introduce the non familiar reader

to some of the technical terms used along the paper.

In chapter 3, the internal algorithms of the

simulator are described, focusing in the geometrical

representation and its usage.

In chapter 4, the efficiency results from the

geometrical representation and the simulation test

are shown.

Finally, the conclusions and the future work are

exposed.

2 STATE OF THE ART

The NC machining simulation using computer

graphics techniques is a widely extended research

topic.

Some traditional approaches do not store the

geometrical information during the simulation, but

they simply modify the drawing screen using an

image-based approach.

There are solutions that store in the computers

memory the intermediate result, having an internal

3D geometric representation of the object that is

changed dynamically during the simulation. This

allows a permanent representation and point of view

independency of the object, better geometric

accuracy control, collision detection, etc.

Van Hook (Van Hook, 1989) used an extended

Z-buffer data structure (called a Dexel structure) for

the graphical verification. In his paper he presented a

scan method to convert surface data into his Dexel

(depth element) structure, and to store Z values for

the nearest and the farthest surface at each Dexel.

This technique has been extended by several authors

(Zhu, 2004).

Another traditional CG techniques for the

geometric representation include i) B-Rep ii) CSG,

and iii) Hierarchical Space Decomposition.

Although B-Rep is the most used method for the

solid modeling in modern CAD systems, its

straightforward use for machining simulation is

mainly impaired by the long time required for

simulation (Spence, 2001). A similar problem occurs

with CSG representation, with computational costs

of order O(n

), where n is the number of primitives

(Stewart, 2003) being computationally expensive.

To cope with the complexity of the problem and

the long time required in these approaches, the

approximation of the exact geometry, and especially

the partitioning of the object in suitable regions has

been proposed by several authors (Stewart, 2003).

The most classic technique for volume

partitioning is the voxel representation (classical

octree, extended octree (Brunet, 1990), SP-Octree

(Cano, 2002)) that combines the space partitioning,

solid representation and boolean operation support

in a single definition.

Maeng et al (Maeng, 2003) have used the Z-map

scheme, where the work piece is approximated as a

set of z-axis aligned vectors, that restricts the

application to the 3-axis NC machining.

The level (or slice) based representation is

widely used in the computer assisted telemedicine to

generate 3D models from 2D layers (scanners,

CATs) (Fujimori, 2004). However, the support for

true real time visualization is not easily

accomplished.

In this paper, we present a level-based solid

representation. Although some similarities can be

found with the level approximation of the

telemedicine area, the main difference of this work

is the orientation towards boolean operations.

3 PROPOSED REPRESENTATION

In this chapter, we will introduce the simulator

components. For a deeper explanation about the

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

358

high-level architecture and the module definition, we

refer the reader to (Moreno, 2004).

Figure 1: A LBR parallelepiped is shown in solid mode

(left) and its approximation in levels (right).

3.1 Boolean Operation Support

The chosen geometrical representation for the

machined objects is a level-based representation,

consisting of using a set of parallel levels to

represent the 3D object. Each level is a set of non-

intersecting and coplanar polygons with at least

three vertices. The distance between the levels is

defined as ∆ and it defines the maximum detail that

can be perceived. We call LBR (Level-Based

Representation) this representation and LBR object

to the object represented using the LBR

representation (see Figure 1).

The LBR representation provides a direct way to

perform boolean operations between LBR objects: a

3D boolean operation is simplified in a set of 2D

boolean operation between two 2D polygons, that is

a well reviewed research topics (Vatti, 1992),

(Preparata, 1985) (see Figure 2).

Figure 2: A boolean operation example between 2 LBR

objects.

3.2 Spatial Partitioning

The efficiency of the polygon clipping algorithms

depends directly on the total number of contours and

points involved in the boolean operation (Leonov,

1998):

O(n log*n + k + z log n) (1)

where n is the number of edges (points), z is the

number of contours and k is the number of edges

intersections.

Table 1: Pseudo Code algorithm for the boolean operation

between the stock and the tool (LBR Objects).

OpBool (in-out LBR_Object stock, in LBR_Object sweep)

for-each section S in both objects

for-each level L in the section S

stock[S][L]=PolygonClip2D (stock[S][L], sweep[S][L])

end for-each

As the simulation is performed, the working piece

gets more complex and in consequence, the number

of points and contours grows. In order to limit the

number of points and contours that would increase

the boolean operation time, a high-level partitioning

system is added to the object definition.

This spatial partitioning decomposes the objects

into a set of smaller regions, each of them being a

set of parallel levels, as it was exposed previously.

Putting all this together, the boolean operation

pseudo-algorithm is shown in Table 1.

3.3 Performance

The overall computational cost is reduced since the

classical boolean operation between geometrical

objects is O(n

) (Poutrain, 2001) and this approach

reduces the computational cost to O(n*m) where n is

the number of levels and m is the number of

contours of the levels.

3.4 Model Reconstruction

The rendering of the LBR objects requires the

reconstruction of the set of levels. These levels must

be joined together in order to obtain a 3D polygonal

object. This process is called model reconstruction.

Several authors have solved this problem from a

non-real time point of view. For example, the use of

marching cubes techniques (Nielson, 2003) is one of

the most widely used techniques for the

A GEOMETRIC REPRESENTATION FOR THE REAL-TIME SIMULATION OF NC MACHINING PROCESSES

359

reconstruction of polygonal meshes from a set of

3D contours.

But due to its computational cost, the marching

cubes technique is not suitable for a real-time

material removal simulator.

In order to exploit the temporal and spatial

coherency of the machined object, two consecutive

levels are joined with a set of polygons only if every

contour knows with which contour has to be joined

in the next level (see Figure 3a).

This connectivity information is achieved during

the simulation process, since all the contours are

generated by known tool movements. The

movement identifier is used to determine which

contours must be joined to reconstruct the object.

Figure 3: A LBR solid mechanized with a ball-end tool.

Rendered a) joining consecutive levels, and b) extruding

each level towards the next one.

There exist cases and special conditions where a

level contour can not be joined with any other. This

is specially noticeable when the tool passes several

times by the same area or when the number of inner

contour are so complex, that it is uncertain how to

join them. In these cases, there is not enough

information to reconstruct that object portion or slice

so a special and simpler algorithm is used. This

algorithm extrudes a level perpendicularly towards

the next one (see Figure 3b), but the quality of the

graphical output decreases.

The combination of both algorithms makes

possible the rendering of level-based represented

objects at interactive frame rates, even during the

simulation process. Applying visualization

techniques, the reconstruction is performed in those

elements (regions and levels) that are visible,

optimizing the number of triangles sent to the

graphical API (OpenGL in our case).

4 RESULTS

In order to test the efficiency of the presented solid

representation, we have chosen two different

approaches: i) the behaviour of the LBR boolean

operation depending on the number of levels and

regions, and ii) the simulation times when the

simulator is running under final conditions.

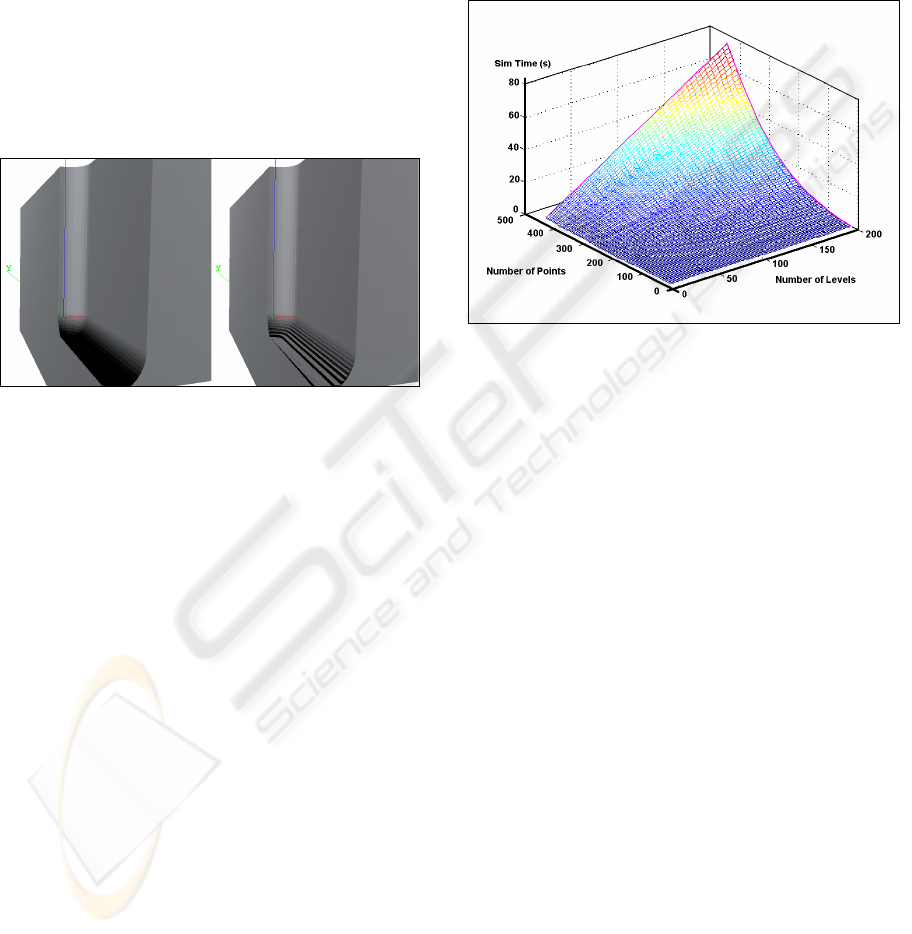
Figure 4: A 3D graphic where the axis are: Simulation

time (Y), number of Points (X) and number of Levels (Z).

The simulation time measures the execution time

performing a single 3D boolean operation between two

LBR solids with the given points and levels and a single

region.

The first test set is oriented to study the

computational cost in a single 3D boolean operation

between two LBR solids (see Figure 4) varying the

number of points and the number of levels for a

given set of boolean operation.

The main conclusions deduced from the results

confirms the theory. The number of levels increases

the computational effort in a linear way (each level

has to execute an internal 2D boolean operation) and

the number of points following a non-linear

function, due to the 2D boolean operation cost (see

formula 1).

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

360

Figure 5: A 3D Number of Regions Efficiency. The same

model has been executed with different number of regions.

In this example, the optimal number of regions is a 10 x 8

decomposition.

The next test set studies the simulation time

behavior varying the number of regions of a single

LBR solid (see Figure 5). Seeing the results, it is

noticeable that, if the number is low, the

computational cost is high. As the number of regions

increases, the computational cost falls till an upper

limit is reached. Going further this limit does not

improve the efficiency, but it worsen it.

Table 2: Simulation times for three test models with

different complexity varying the number of regions. The

factor is calculated dividing the given time with the real

machining time. The complexity of each model is a

subjective qualifier and it is intended to classify the

models in easy and difficult models, depending on the

achieved results after some number of simulations.

This lead us to a uncertain problem: how to

decide the number and distribution of the regions. In

the presented table, the optimal value is different

from each other, so there is no global optimal value.

A workaround for this problem is to classify the

models in different types, each one with common

properties. It is expected that similar models have

similar number of regions as optimal value. Then,

during the simulator initialization, the user informs

the model type he is going to simulate and

internally, the pseudo-optimal values are chosen. We

refer the reader to the future work to see what is

planned to solve definitively this problem.

The final test set is focused in the runtime

efficiency and the synchronization between the

simulator graphical output and the real NC machine

feedback. Different models has been tested in the

simulator and the times of three of them has been

tabulated in Table 2.

The synchronization is achieved when the

simulation time and the machining time are similar.

For testing purposes, we have considered that five

seconds delay is the proper limit to considerate that a

model has been simulated properly. Following this

criterion, just two complex models don’t complain

with the requirements (see third row in Table 2 to

see the details of one of them). The other models

have been correctly simulated.

The results show that with small and medium NC

programs, a synchronized simulation is achieved,

obtaining an interactive visualization and a quite

good graphical output. The reader must take into

account that the graphical hardware is limited (12”

monitor with 800x600 resolution (max)).

With complex models, the simulator becomes

sensible to the initial parameterization. In the tests,

the perfect synchronization has been achieved, but

several preliminary test have been performed in

order to set the proper initial parameters. This

simulator problems will be solved in the future (see

future work section for more details).

5 CONCLUSIONS

The main goal of this work was to present how a

level-based representation is used as the kernel of a

material removal simulator, being able to achieve

real time execution when it is used embedded in a

real NC machine (see Figure 6).

The results in chapter 4 confirm that a proper

real-time simulation is achieved with interactive

rates and a sufficient image quality taking into

Model

(Complexity)

Num

Regions

Simulation

Time (s)

Factor

Test-1

( Low )

1x1

2x2

4x2

8x2

Real Mach.

1740 301

221 174

170

10.2

1.7

1.3

1.02

1.0

Test-2

( Medium )

1x1

2x4

4x8

8x16

Real Mach.

2020 228

211 305

210

9.6

1.10

1.01

1.45

1.0

Test-3

( High )

1x1

4x2

8x4

8x8

16x16

Real Mach.

4215 920

509 470

554 450

9.3

2.04

1.13

1.04

1.23

1.0

A GEOMETRIC REPRESENTATION FOR THE REAL-TIME SIMULATION OF NC MACHINING PROCESSES

361

Figure 6: Some simulation results. From left to right: 2D milling, 2.5D lathe, 3D milling and C-axis lathe.

account that the available hardware resources are

limited.

The hardware employed for all the tests is an

AMD K6 1500 processor with a GForce 2 with

32Mb and a 800 x 600 resolution. The NC machine

is a 8070 CNC from Fagor Automation.

6 FUTURE WORK

In order to achieve the best efficiency of the

simulator, the optimal parameter values must be

chosen depending on the concrete NC program that

will be executed. This setup is estimated a priori and

a profile list is created with the pseudo-optimal

parameter values for each simulation type.

This strategy has a big problem. There will be

operations that will not be simulated as expected,

with the need of changing the simulation parameters.

Other related problem is that the chosen parameter

values are static along a simulation, being

impossible to change them if it is necessary.

The addition of a predictive control to the

simulation core is the solution for this kind of

problems. It will monitor some variables, modifying

the simulation parameters following a small set of

rules. We have to define which are the variables that

will be monitored, the rules that are applied and the

which variables will be updated. Each variable

changing action is associated with one action and its

computational cost. The action will be executed if it

worth, speaking in computational cost terms.

Increasing the NC machine hardware

capabilities, a more sophisticated visualization

rendering should be added to the simulation

pipeline. This would improve the achieved graphical

output, increasing the realism of the simulator. For

example, we are planning to use shading techniques

for the global illumination and to modify the texture

of the working piece with heat dependent color.

ACKNOWLEDGMENTS

This work is sponsored by the Basque Government

under INTEK program. The authors would like to

express their gratitude to the SIMUMEK partners

(FAGOR Automation S. Coop, SOME Sistemas

Informaticos and Alecop, S. Coop) for their

collaboration.

REFERENCES

Brunet, P., Navazo, I., 1990, Solid representation and

operation using extended octrees. In ACM

Transactions on Graphics 9, 2 (1990), pp. 170-197.

Cano, P., 2002, Representation of polyhedral objects using

sp-octrees. In Journal of WSCG 10, 1 (2002), pp. 95 -

101.

Fujimori, T., Suzuki, H., Kobayashi, Y., Kase, K., 2004,

Contouring medial surface of thin plate structure

using local marching cubes. In Shape Modeling

Applications, 2004. Proceedings 2004 pp. 297 – 306.

Leonov, M. V., 1998, Implementation of boolean

operations on sets of polygons in the plane. In BS

Thesis (in Russian), Novosibirsk State University,

1998.

Maeng, S. R., Baek, N., Shin, S. Y., Choi, B. K., 2003, A

fast Z-map update method for linearly moving tools. In

CAD, 35(11):995-1009, 2003.

Moreno, A., Toro, C., Arizkuren, I., Segura, A., Posada,

J., 2004, Development of an advanced 3d graphic

simulation system for milling and lathe CNC

machining, Topics 16, 4 (2004), p. 23.

Nielson, G. M., 2003, On marching cubes. In

Visualization and Computer Graphics, IEEE

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

362

Transactions on Volume 9, Issue 3, July-Sept. 2003

pp. 283 - 297.

Poutrain, K., Contensin, M., 2001, Dual B-Rep-CSG

collision detection for general polyhedra. In Computer

Graphics and Applications, 2001, Proceedings. Ninth

Pacific Conference on 16-18 Oct. 2001 pp. 124 - 133.

Preparata, F. P. , Shamos, M. I., 1985, Computational

Geometry: An Introduction. Springer-Verlag, New

York, NY, 1985.

Spence, 2001, Parallel processing for 2-1/2D machining

simulation. In Proceedings of the sixth ACM

symposium on Solid modeling and applications, 2001,

Ann Arbor, Michigan, United States Pages: 140 - 148.

Stewart, N., Leach, G., John, S., 2003, Improved CSG

Rendering using Overlap Graph Subtraction

Sequences. In International Conference on Computer

Graphics and Interactive Techniques in Australasia

and South East Asia - GRAPHITE 2003, pp. 47 - 53.

Van Hook, 1986, Real Time shaded NC Milling Display.

SIGGraph86, Volume 20, Number 4, pp. 15 - 20.

Vatti, B. R., 1992, A Generic Solution to Polygon

Clipping. In Commun ACM 35 1992, pp. 56 - 63.

Zhu, W., Lee, Y., 2004, Product prototyping and

manufacturing planning with 5-DOF haptic sculpting

and dexel volume updating. In Haptic Interfaces for

Virtual Environment and Teleoperator Systems 2004

(HAPTICS '04). Proceedings, pp. 98-105.

A GEOMETRIC REPRESENTATION FOR THE REAL-TIME SIMULATION OF NC MACHINING PROCESSES

363