SILHOUETTE DETECTION FOR ADAPTIVE POLYGONAL MESH

SIMPLIFICATION USING DISTANCE TRANSFORMS

Susana Mata and Luis Pastor

Dpt. de Informática, Estadística y Telemática, U. Rey Juan Carlos

C. Tulipán, s/n., 28933 Móstoles, Madrid, Spain

Angel Rodríguez

Dept. de Tecnología Fotónica, U. Politécnica de Madrid

Campus de Montegancedo s/n, 28660 Boadilla del Monte, Spain

Keywords:

Computational Geometry and Object Modelling, Three Dimensional Graphics and Realism, Picture and Image

Generation.

Abstract:

Distance Transforms have proven to be useful for many image processing applications. Nevertheless, they

have only recently started to be used in computer graphics environments. The goal of this paper is to propose

a new technique based on Distance Transforms for detecting mesh elements which are close to the objects’

external contour (from a given point of view), and using this information for weighting the approximation

error which will be tolerated during the mesh simpliﬁcation process.

1 INTRODUCTION

The number of ﬁelds using three dimensional graph-

ics is constantly increasing. Different areas like medi-

cine, education, training, leisure, etc. are more and

more taking advantage of the beneﬁts that 3D visual-

ization can bring to them.

Representing objects is one of the key stages of any

computer graphics system. Among the mainstream

models in this ﬁeld, the most extended technique for

representing the surface of objects is based on polyg-

onal meshes, being the simplicity of its basic elements

one of the underlying reasons (Watt, 2000).

However, polygonal meshes need a large number

of polygons for approximating real objects with a

reasonable accuracy. Whenever computation time is

a concern, techniques which decrease the model’s

polygon count while keeping an acceptable visual

appearance are mandatory. An approach that has

been widely investigated is multiresolution mod-

elling, which consists in representing objects at dif-

ferent resolution levels and choosing the proper ap-

proximation according to the visualization conditions

(Xia and Varshney, 1996; Hoppe, 1997). Basic princi-

ples of this approach were set by James Clark (Clark,

1976); comprehensive surveys can be found at (Puppo

and Scopigno, 1997; Garland, 1999; Luebke, 2001;

Luebke et al., 2003; Floriani et al., 2004).

The key point is to obtain a simpliﬁed model us-

ing less computational resources but looking similar

to the original one when rendered under certain con-

ditions. No attention needs to be paid to features not

observable by the end user. Moreover, some details

in a model become more obvious than others to a hu-

man viewer. For example, silhouettes are known to be

critical for the ﬁnal visual quality appreciated by our

visual system (Luebke and Erikson, 1997).

The goal of this paper is to propose a new tech-

nique that allows taking into account the proximity

of a mesh element to the mesh’s external contour for

weighting the approximation error which will be tol-

erated during the simpliﬁcation process. More specif-

ically, the contributions of this work can be brieﬂy

summarized as follows:

• Analyzing the applicability of Distance Transforms

for detecting the proximity of mesh elements to the

external silhouette.

• Proposing mesh simpliﬁcation criteria based on

a precomputed silhouette proximity measure, ob-

tained by means of a Distance Transform.

• Presenting a simpliﬁcation technique using a Dis-

tance Transform for selecting the allowed approxi-

mation error in regions close to the external silhou-

ette.

The rest of the paper is organized as follows: Sec-

tion 2 presents a short overview of some previous

work related to mesh simpliﬁcation algorithms and

the different approaches to identify and preserve the

model’s silhouette. A brief introduction to basic

Mata S., Pastor L. and Rodríguez A. (2006).

SILHOUETTE DETECTION FOR ADAPTIVE POLYGONAL MESH SIMPLIFICATION USING DISTANCE TRANSFORMS.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 43-50

DOI: 10.5220/0001353800430050

 SciTePress

concepts of digital Distance Transforms and Multi-

Tessellation is also included. Section 3 describes the

proposed approach, while Section 4 shows some ex-

perimental results. Finally the conclusions and future

work are presented in Section 5.

2 PREVIOUS WORK

2.1 Mesh Simpliﬁcation

Many mesh simpliﬁcation techniques have been pro-

posed during the last years. Among the methods

based on objective metrics, work has been done in or-

der to incorporate other attributes besides geometry

like color, texture or normals (Garland and Heckbert,

1998; Cohen et al., 1998). Perceptual metrics have

also been developed (O’Sullivan et al., 2004; Cheng

and Boulanger, 2005); Lindstrom and Turk use an im-

age metric to guide the simpliﬁcation process (Lind-

strom and Turk, 2000). Reddy introduced a percep-

tive model to guide the selection of the appropriate

level of detail (Reddy, 1997). (Luebke, 1998) de-

ﬁned a contrast sensitivity function that predicts the

perception of visual stimuli. Some of the perceptu-

ally driven simpliﬁcation methods explicitly pursue a

good silhouette preservation, deﬁning normal cones

(Williams et al., 2003). Good silhouette approxi-

mation through contour computation in image space

has also been researched (Raskar and Cohen, 1999;

Sander et al., 2000).

The approach presented here not only identiﬁes the

objects’ silhouette. It performs also a mesh elements’

explicit classiﬁcation in object space, attending to its

proximity to the external contour from a given point

of view.

2.2 Digital Distance Transforms

Measuring the distance between image elements may

be of interest for further processing in many image

analysis applications. Basics concepts regarding dig-

ital distances can be found in (Rosendfeld and Pﬂatz,

1966; Rosendfeld and Pﬂatz, 1968).

The application of a Distance Transform to an im-

age (usually binary) produces as output a distance

image, where each element of this distance-image is

assigned a distance label. For any element its label

stores a value indicating its closest distance to the

background. Therefore, the computed distance image

can be seen as a grey-level image where the intensity

level identiﬁes the minimum distance to the comple-

ment of the object.

A distance transform can be computed in two steps

by propagating local distances over the image; this is

true for 2D, 3D and higher dimensions (Rosendfeld

and Pﬂatz, 1966). Initially, the elements belonging to

the object are set to inﬁnity and the elements belong-

ing to the background are set to 0. In the case of a

2D image, during the ﬁrst step the image is analyzed

from top to bottom and from left to right. During

the second step, the image elements are visited from

right to left and from bottom to top. Each element

is assigned the minimum value between itself and the

already visited neighbours incremented by their con-

nectivity weight.

Distance transforms and some variations of them

in combination with other image processing tech-

niques can be applied for representing and analyzing

3D objects in multiple applications (Nystrom, 1997;

Svensson, 2001; Sintorn, 2005). Distance ﬁelds have

also been applied in computer graphics environments,

such as in collision detection (Teschner et al., 2004).

However, digital distance transforms can be used

in other ﬁelds that have not been explored so far. The

work presented here aims to open a way for new ap-

plications of Distance Transforms within computer

graphics environments.

2.3 Multi-Tessellation

The Multi-Tessellation method, originally called

Multi-Triangulation, was introduced by De Floriani et

al. (Floriani et al., 1997). It provides a general mul-

tiresolution framework for polygonal meshes offering

several attractive features, like selective reﬁnement,

locality or dynamic update (Floriani et al., 1998).

Multi-Tessellation, MT for short, is a hierarchical

model deﬁned as a directed acyclic graph, where the

nodes represent mesh updates and arcs represent de-

pendencies between updates labelled with sets of tri-

angles. Each triangle t may have associated a global

approximation error, describing the difference be-

tween t and the surface patch it approximates. Simpli-

ﬁcation applications may be adapted in order to build

an MT while performing the simpliﬁcation process.

Once the MT has been built, it can be queried at run

time for extracting a simpliﬁed mesh fulﬁlling some

deﬁned restrictions.

Two kinds of criteria can be deﬁned for selectively

reﬁning the mesh:

• A threshold function, used to bound the approxi-

mation error.

• A focus condition, used to set the region of interest

under which the query will be evaluated.

The distributed package (Geometric Modeling and

Computer Graphics Research Group. DISI - Dipar-

timento di Informatica e Scienze dell’Informazione

University of Genova, 2005) implements a hierarchy

of classes that permit the construction of an MT by

adapting a simpliﬁcation method in order to perform

some basic MT operations. Some useful threshold

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

and focus conditions are already implemented, in-

cluding point location, region intersection, etc. Ad-

ditionally, an executable implementing the Jade sim-

pliﬁcation technique is provided (Ciampalini et al.,

1997). In this case, the simpliﬁcation algorithm is

based on vertex decimation operators.

Deﬁning new focus and threshold conditions can be

easily done by adding new classes to the library. This

sets a general and useful framework for dynamically

managing the level of detail of a particular represen-

tation.

The MT package has been used in this work to

present the results obtained by integrating the pre-

computed distance to silhouette into the threshold

function.

3 METHOD DESCRIPTION

The approach followed here classiﬁes the mesh faces

or vertices attending to their proximity to the external

silhouette from a certain point of view. The classiﬁ-

cation process uses a Distance Transform, computed

over the mesh elements’ projection on the visualiza-

tion plane. This transform provides for each element

its distance to the projected contour, being useful for

extracting the mesh elements which compose or are

located near the mesh silhouette for any particular

point of view.

Previous to the projection stage, a 2D grid is cre-

ated on the visualization plane. This grid needs a res-

olution level that has to be selected according to the

input mesh level of detail, the desired simpliﬁcation

degree and the available time to perform the simpli-

ﬁcation procedure. Every cell in the 2D grid has a

list associated containing the indexes of the faces that

project into it. The occupancy of the grid cells can be

represented as a binary image; it is over this binary

image where Distance Transforms can be computed.

Last, a classiﬁcation of the model faces can be ob-

tained backprojecting the distance labels to the mesh

faces that map into each grid cell.

The same process can be applied for backproject-

ing the distance values to the vertices instead of to the

faces. The tags assigned to the polygonal mesh ele-

ments can then be used in different ways to guide the

simpliﬁcation process, providing a criterion for modi-

fying locally the approximation error allowed in areas

close to the external contour.

It must be highlighted that the ﬁrst three steps are

performed in a pre-processing stage, producing a la-

belled polygonal mesh which will be used later on

during the simpliﬁcation stage. The following Sec-

tions describe each of the method’s stages.

3.1 Mesh Mapping

Silhouettes are view-dependent features. For that rea-

son, their extraction must be done for a certain view

point. Given a visualization plane, the 3D mesh is

projected on it by applying the proper projection ma-

trix to each vertex coordinates. In order to extract the

object’s silhouette, it is necessary to create a binary

image where distance measurements can be carried

out. For that purpose the visualization plane is parti-

tioned into cells forming a grid which can be seen as

a 2D digital image. The number of cells making up

the grid is analogous to the image resolution; conse-

quently the parameterization of this value allows the

analysis at different resolutions.

Every face belonging to the projected polygonal

mesh is tested to ﬁnd the cells of the 2D grid with

which it intersects.

A data structure is updated where every grid ele-

ment keeps track of the faces intersecting with it. This

way, the posterior backprojection of distance values

is straightforward. This procedure is computationally

expensive, but affordable as pre-processing.

The binary image is extracted from the grid occu-

pancy information, setting as object every cell with

any face mapping over it.

3.2 Distance Transform

Computation

Once the 2D image is obtained, the next stage consists

in obtaining a distance image by applying a distance

transform to the binary image. The result is a new

image where the assigned intensity values increase as

the pixel gets further away from the background.

3.3 Mesh Labelling

At this point, the distance of an object pixel to the

background has already been computed. Previously,

the correspondences between pixels and the facets

mapping into them have also been calculated. There-

fore, the labelling of every face with a value repre-

senting its distance from the background is a simple

process. The distance label of a pixel, which is equiv-

alent to a grid cell, is assigned to all the faces that

intersect with the cell.

As a result, a labelled mesh is obtained where every

face stores a value representing its proximity to the

external contour.

The same approach may be followed when the dis-

tance label is assigned to vertices or edges instead of

faces. Figure 1 shows the results of backprojecting

the distance values onto the mesh. Fig. 1(a) shows

a rendered view of the original mesh. Fig. 1(b) and

1(c) represent the same mesh under different points of

SILHOUETTE DETECTION FOR ADAPTIVE POLYGONAL MESH SIMPLIFICATION USING DISTANCE

TRANSFORMS

(a) Original mesh (b) Mesh in Figure 1(a) rotated 180 de-

grees over the X axis, with grey levels

proportional to the distances to the ex-

ternal silhouette

over the X axis, with grey levels propor-

tional to the distances to the external sil-

houette

Figure 1: Backprojection of distance values in image 1(a) over the 3D model. Mesh vertices color represent the backprojected

distance label.

view. The grey levels in the images represent distance

to the silhouette (lighter intensities represent higher

distances to the contour).

3.4 Mesh Simpliﬁcation

The method’s last stage is also the ﬁnal goal of the

whole process, where the extracted distance values

are used for mesh simpliﬁcation purposes.

The use of the distance labels depends on the se-

lected simpliﬁcation technique. The work presented

here has been based on the Jade approach, a ver-

tex decimation technique based on the global er-

ror (Ciampalini et al., 1997). The distance infor-

mation is computed for the vertices of the original

mesh. Since the vertices belonging to a simpliﬁed

model are a subset of the original mesh, the precom-

puted distance labels are valid for any level of detail.

Multi-Tessellations obtained through the application

of the Jade method are freely distributed with the MT-

Package.

The proximity of every facet to the external con-

tour is taken into account in the extraction stage. This

means that for a given error threshold, the error al-

lowed in regions close to the external silhouette is re-

duced according to a predeﬁned law.

The implemented solution, requires the deﬁnition

of two parameters:

• Distance interval: range of distance labels which

identify the region where a more accurate approxi-

mation is desired.

• Error factor: the purpose of this parameter is to de-

ﬁne an error threshold for the portion of the mesh

within the region of interest. This threshold, differ-

ent from the global error threshold, is deﬁned as a

function of the global error threshold.

The width of the contour area can be simply modi-

ﬁed by changing the range of distance labels that de-

ﬁne the region of interest. In our case, the range is

deﬁned by setting a threshold over the minimum dis-

tance of the vertices belonging to a face. Other solu-

tions can be easily devised.

The error factor allows to reﬁne the quality of the

approximation in the contour region taking into ac-

count the threshold error ﬁxed for the rest of the

model. This way, the allowed error in the contour

is f · e, where e is the error permitted in the rest of

the model and f is the error factor. Again, other error

functions are also feasible.

4 RESULTS

The experimental results presented in this section

were obtained by applying the technique previously

described to the Multi-Tessellation models distributed

together with the MT-Package.

Figure 2(a) shows the simpliﬁcation of the mesh

obtained by imposing a restrictive error threshold over

the silhouette. In this case, the error factor was set to

0, meaning that no error is allowed on the external

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

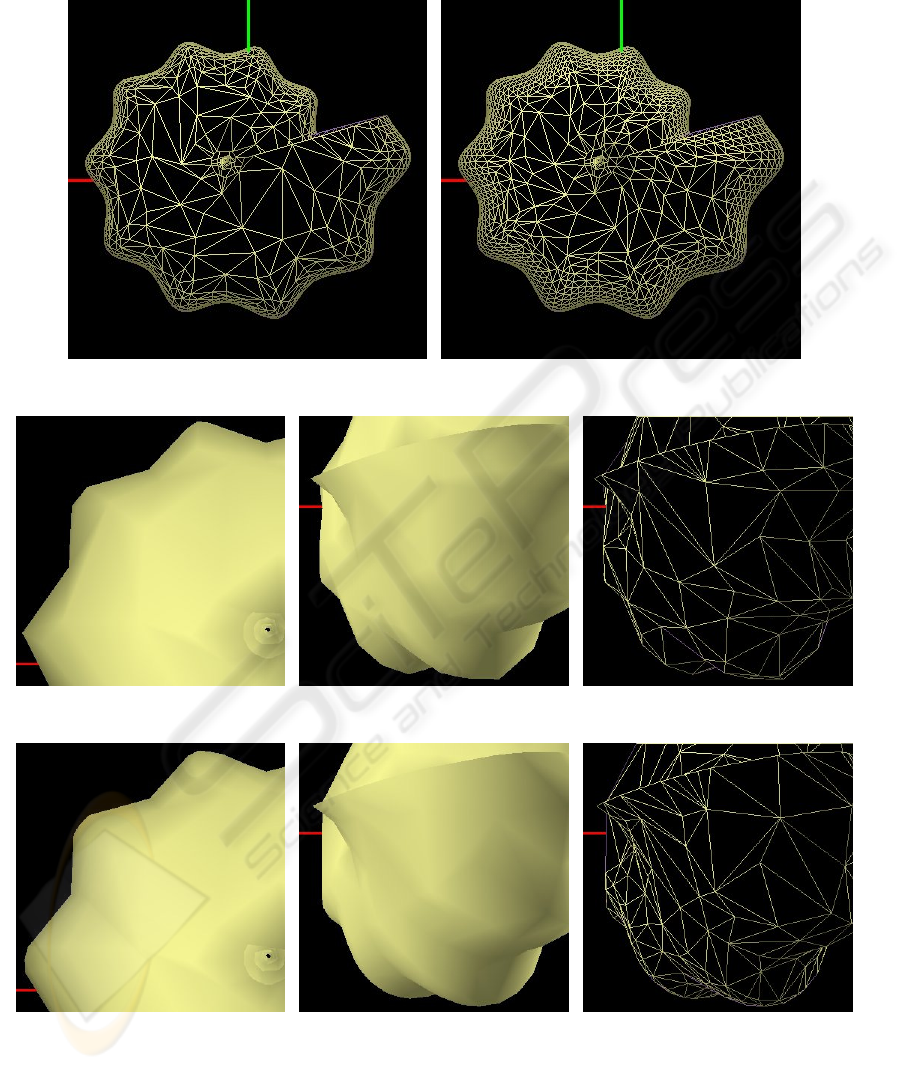
(a) Result of simplifying mesh elements with dis-

tance values larger than 2

(b) Result of simplifying mesh elements with dis-

tance values larger than 15

pliﬁcation

(d) The same simpliﬁed mesh from an-

other point of view

(e) Wire mesh of 2(d)

(f) Close-up view after the Distance

Transform based simpliﬁcation

(g) A Distance Transform based sim-

pliﬁcation for a different point of view

(h) Wire mesh of 2(g)

Figure 2: Shell example.

SILHOUETTE DETECTION FOR ADAPTIVE POLYGONAL MESH SIMPLIFICATION USING DISTANCE

TRANSFORMS

(a) Close-up view of the mesh simpli-

ﬁed with the Jade method

(b) Another perspective of the result af-

ter the Jade simpliﬁcation

(d) Close-up view of the mesh simpli-

ﬁed with proposed method

(e) A Distance Transform based simpli-

ﬁcation for a different point of view

(f) Wire mesh of 3(e)

Figure 3: Abstract geometric example.

contour. The region of interest (the mesh portion con-

sidered to be near the silhouette) is made up of faces

whose vertices have a minimum distance label less

than or equal to 2. It can be seen that the rest of the

mesh is coarser (it has suffered a strong simpliﬁca-

tion process), while the density of triangles over the

silhouette is extremely high.

The algorithm presented here allows an easy para-

meterization of the width of the contour area, as it can

be appreciated in Figure 2(b). It can be seen how the

region of high resolution extends itself towards the in-

terior of the object.

Figures 2(c) and 2(f) show two simpliﬁed meshes

with approximately the same number of polygons,

1074 and 1077 respectively, obtained with two meth-

ods: the Jade and the distance-based approach pro-

posed here. Figures 2(d) and 2(g) show the simpli-

ﬁcation from a different point of view. Figure 2(d)

(1226 triangles) has been obtained from Jade simpli-

ﬁcation, while Figure 2(g) has been obtained using

the distance information. A perceptible improvement

in the smoothness of the silhouette can be appreciated

in both Fig. 2(f) and 2(g). A wireframe rendering of

the model reveals a higher density of facets close to

the external contour in Fig. 2(h) with respect to 2(e).

Figure 3 shows some results of simpliﬁcations ap-

plied to the model shown in Fig. 1(a). Figure 3(a)

(612 triangles) is the simpliﬁed model extracted from

Jade simpliﬁcation method, while Fig. 3(d) (600 tri-

angles) represents the simpliﬁcation using distance

information. Under a different rotation, the simpli-

ﬁcation is carried out using distance labels in 3(e)

(510 triangles) while in Fig. 3(b) (508 triangles) no

distance information is taken into account. Again,

the smoothness of the silhouette is higher with our

method and the mesh density increases in the prox-

imity of the external contour, as shown in Fig. 3(c)

(without distance information) and 3(f) (with distance

information).

It can be observed that the approximation in the sil-

houette is noticeable better with our method.

Regarding computational issues, cost in terms of

memory requirements is only of one extra value per

vertex. In case of tagging the mesh faces or mesh

edges an additional value per tagged element would

be required. With respect to computational cost, it

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

has to be noted that all the heavy computation is per-

formed at pre-processing time. The most expensive

step is the mesh mapping over the 2D grid, in or-

der to collect the information needed for backproject-

ing the distance values. Efﬁcient implementations for

these operations using spatial data partitioning could

be considered. As it was explained above, the com-

putation of the Distance Transform can be performed

involving only two passes over the 2D image.

5 CONCLUSIONS AND FUTURE

WORK

Simpliﬁcation algorithms are usually guided by some

criteria in order to select which elements of the

mesh shall be removed or replaced. Introducing

precomputed distance labels as part of the guiding

metrics is a straightforward process, opening a new

way to design a range of techniques which are use-

ful for including perceptually motivated criteria in

mesh simpliﬁcation algorithms. The results presented

here suggest that the use of distance information is

a promising approach for mesh simpliﬁcation tech-

niques, since adding distance labels to mesh ele-

ments provides more information than the conven-

tional methods based on the extraction of the silhou-

ette edges.

The fact that distance information can be assigned

to any element of the mesh (vertices, edges or faces)

facilitates adapting these techniques to a wide range

of simpliﬁcation methods. The nature of the basic un-

derlying operator (vertex removal, edge collapse, etc)

does not impose additional limitations. Furthermore,

the applicability of distance labels goes from off-line

simpliﬁcation processing to run-time selective reﬁne-

ment.

The work presented here computes the mesh ele-

ments’ distance to the extended contour given a pre-

deﬁned point of view. Future work includes:

• Extending the method for covering all possible

points of view in a way which is both performant

and computationally efﬁcient.

• Integrating distance to the silhouette into other

mesh simpliﬁcation methods besides the Jade

method.

• Extending the method in order to consider also in-

ternal silhouettes.

ACKNOWLEDGMENTS

This work has been partially funded by the Span-

ish Ministry of Education and Science (grant

TIC2003-08933-C02) and Government of the Com-

munity of Madrid (grants GR/SAL/0940/2004 and S-

0505/DPI/0235).

The authors also thank to the Geometric Modelling

and Computer Graphics Research Group for distrib-

uting the MT-Package.

REFERENCES

Cheng, I. and Boulanger, P. (2005). A 3D perceptual met-

ric using just-noticeable-difference. In Proc. of Euro-

graphics 2005.

Ciampalini, A., Cignoni, P., Montani, C., and Scopigno, R.

(1997). Multiresolution decimation based on global

error. In The Visual Computer, volume 13 of 5, pages

228–246.

Clark, J. H. (1976). Hierarchical geometric models for visi-

ble surface algorithms. Communications of the ACM,

19:547–554.

Cohen, J., Olano, M., and Manocha, D. (1998).

Appearance-preserving simpliﬁcation. InProceedings

of SIGGRAPH 98, pages 115–122.

Floriani, L. D., Kobbelt, L., and Puppo, E. (2004). A

survey on data structures for level-of-detail models.

In N.Dodgson, M.Floater, and M.Sabin, editors, Pro-

ceedings MINGLE Workshop 2004. Springer Verlag.

(to appear).

Floriani, L. D., Magillo, P., and Puppo, E. (1997). Building

and traversing a surface at variable resolution. In Pro-

ceedings of IEEE Visualization 97, pages 103–110.

Floriani, L. D., Magillo, P., and Puppo, E. (1998). Efﬁcient

implementation of multi-triangulations. In Proceed-

ings of IEEE Visualization 98, pages 43–50.

Garland, M. (1999). Multiresolution modeling: Survey &

future opportunities. In EUROGRAPHICS’99.

Garland, M. and Heckbert, P. (1998). Simplifying surfaces

with color and texture using quadric error metrics.

In Proceedings of IEEE Visualization’98, pages 263–

270.

Geometric Modeling and Computer Graphics Research

Group. DISI - Dipartimento di Informatica e Scienze

dell’Informazione University of Genova (2005). The

MT (Multi-Tesselation) Package. Web.

Hoppe, H. (1997). View-dependent reﬁnement of progres-

sive meshes. In SIGGRAPH’97, Computer Graphics

Annual Conference Series, pages 189–198. ACM.

Lindstrom, P. and Turk, G. (2000). Image-driven simpliﬁ-

cation. In ACM Transactions on Graphics, volume 19

of 3, pages 204–241.

Luebke, D. and Erikson, C. (1997). View-dependent sim-

pliﬁcation of arbitrary polygonal enviroments. In Pro-

ceedings of SIGGRAPH 97.

Luebke, D., Reddy, M., Cohen, J. D., Varshney, A., Watson,

B., and Huebner, R. (2003). Level of Detail for 3D

Graphics. Morgan Kauffmann.

SILHOUETTE DETECTION FOR ADAPTIVE POLYGONAL MESH SIMPLIFICATION USING DISTANCE

TRANSFORMS

Luebke, D. P. (1998). View-dependent simpliﬁcation of ar-

bitrary polygonal environments. Ph. D. dissertation,

University of North Carolina.

Luebke, D. P. (May/June 2001). A developer’s survey of

polygonal simpliﬁcation algorithms. IEEE Computer

Graphics and Applications. Faltan las páginas y el

volumen.

Nystrom, I. (1997). On Quantitative Shape Analysis of Dig-

ital Volume Images. Ph. D. dissertation, Uppsala Uni-

versity.

O’Sullivan, C., Howlett, S., Morvan, Y., McDonnell, R.,

and O’Conor, K. (2004). Perceptually adaptive graph-

ics. In Schlick, C. and Purgathofer, W., editors, Eu-

rographics State-of-the-Art Report (EG-STAR), vol-

ume 6, pages 141–164. Eurographics Association, Eu-

rographics Association.

Puppo, E. and Scopigno, R. (1997). Simpliﬁcation, LOD

and multiresolution principles and applications. In

Fellner, D. and Szirmay-Kalos, L., editors, EURO-

GRAPHICS’97, volume16. Tutorial Notes PS97 TN4.

Raskar, R. and Cohen, M. (1999). Image precision sil-

houette edges. In 1999 Symposium on Interactive 3D

Graphics.

Reddy, M. (1997). Perceptually Modulated Level of Detail

for Virtual Environments. Ph. D. dissertation, Univer-

sity of Edinburgh.

Rosendfeld, A. and Pﬂatz, J. (1966). Sequential operations

in digital picture processing. Journal of the Associa-

tion for Computing Machinery, 13(4):471–491.

Rosendfeld, A. and Pﬂatz, J. (1968). Distance functions on

digital pictures. Pattern Recognition, 1:33–61.

Sander, P. V., Gu, X., Gortler, S., Hoppe, H., and Snyder, J.

(2000). Silhouette clipping. In Proceedings of SIG-

GRAPH 2000, pages 327–334.

Sintorn, I.-M. (2005). Segmentation Metohdos and Shape

Descriptions in Digital Images. Ph. D. dissertation,

Swedish University of Agricultural Sciences.

Svensson, S. (2001). Representing and Analyzing 3D Digi-

tal Shape Using Distance Information. Ph. D. disser-

tation, Swedish University of Agricultural Sciences.

Teschner, M., Kimmerle, S., Zachmann, G., Heidelberger,

B., Raghupathi, L., Fuhrmann, A., Cani, M.-P., Faure,

F., Magnetat-Thalmann, N., and Strasser, W. (2004).

Collision detection for deformable objects. In Eu-

rographics State-of-the-Art Report (EG-STAR), pages

119–139. Eurographics Association, Eurographics

Association.

Watt, A. (2000). 3D Computer Graphics. Addison-Wesley.

Williams, N., Luebke, D., Cohen, J. D., Kelley, M., and

Schubert, B. (2003). Perceptually guided simpliﬁca-

tion of lit, textured meshes. In Proceedings of the

2003 Symposium on Interactive 3D Graphics, pages

113–121.

Xia, J. C. and Varshney, A. (1996). Dynamic view-

dependent simpliﬁcation for polygonal models. In

Yagel, R. and Nielson, G. M., editors, IEEE Visual-

ization ’96, pages 335–344.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS