DISCRETE TOOLS FOR VIRTUAL SCULPTURE

Xavier Heurtebise, Sébastien Thon

LSIS, Marseille, France

Keywords: Geometry and modelling, virtual sculpture, voxels, levels of detail, 3D wavelets.

Abstract: In a virtual sculpture project, we represent the material to be sculpted as a set of volume elements (voxels).

Sculpture operations of subtraction and addition are applied on these voxels with tools with various shapes

and sizes. A major advantage of our system is that sculpted objects can then be used as new tools, because

the same model is used for both objects and tools. This is a multiresolution model based on a 3D wavelet

transform. We take advantage of the levels of detail to speed up display and sculpture. However, using

discrete models for objects and tools leads to three problems: important computation time, aliasing when

tools are rotated, and how to perform sculpture operations between discrete objects and tools with different

orientations and sizes. In this paper, we describe our model and then propose solutions to these problems

that allow real-time performance.

1 INTRODUCTION

1.1 Presentation

We present in this paper a multiresolution model

based on 3D wavelets to represent a 3D objects as a

discrete set of volume elements (voxels). Such a

discrete representation is of great use in a virtual

sculpture context as it allows to simulate easily

sculpture operations such as subtraction or addition

of material by simply adding or removing voxels. A

great improvement of our model is its

multiresolution nature given by the use of wavelets,

that allows to accelerate display, interaction and

sculpture operations by the use of levels of detail.

Another major advantage of our system is that we

use this model to represent both objects and tools, so

we can let the user design his or her own tools, by

sculpting them from basic objects. This is an original

approach to virtual sculpture, where most of other

approaches use different models for objects and

tools. However, if other approaches generally use

implicit tools (such as ellipsoids), it is because the

use of discrete tools is a difficult topic, due to three

problems:

− First, this is computationally expensive,

especially when the tool has to be rotated in its

discrete grid of voxels when the tool orientation

is changed.

− Second, there is a degradation of the shape of

the tool due to aliasing if angles of rotation are

not multiple of 90 degrees.

− Third, it is unclear how to perform sculpture

operations such as subtraction or addition

between discrete objects and tools with different

orientations and sizes.

1.2 Previous Works

In this paper, we tackle the problem of virtual

sculpture of 3D objects with tools, both represented

with spatial enumerations. Such a spatial

enumeration is a set of volume elements called

voxels, obtained by sampling the volume of a 3D

object. It can be seen as a 3D image composed of

voxels, where a 2D image is an array composed of

pixels. To make a spatial enumeration from a 3D

object, several methods have already been

suggested. The simplest way is a uniform spatial

enumeration, by regularly sampling the 3D object

into voxels with the same size. However, a major

drawback of this representation is the large number

of voxels needed to represent large objects with

detailed features. This entails three main problems.

The first one is the important memory cost to store

this uniform spatial enumeration. The second one is

that the display of these objects becomes slower.

Finally, operations on these objects such as sculpture

actions or displacements become less and less

interactive.

415

Heurtebise X. and Thon S. (2006).

DISCRETE TOOLS FOR VIRTUAL SCULPTURE.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 415-422

DOI: 10.5220/0001354604150422

 SciTePress

To prevent these inconveniences, adaptive

sampling methods have been developed. Libes

(Libes, 1991) uses an octree to gather groups of

adjacent voxels having same values to reduce the

number of elements stored in memory. It’s very

simple to use and to implement this method. Ferley

(Ferley, 2002) also works on a n-tree where each

cell can be divided in 27 ones. This method looks

like an octree and allows to reach a high level of

detail. However, for an object with small details, the

subdivision level of an octree or n-tree will be very

high. So the processes (construction and use) will be

slow.

Several other sampling methods used in collision

detection propose to modify properties of the voxels,

such as the size, the orientation or even the shape.

With the AABB method (Axis Aligned

Bounding Boxes), Bergen (Bergen, 1997) suggests

to use voxels with different sizes. Gottschalk

(Gottschalk, 1996) proposes to modify not only the

size of the voxels but also their orientation, with the

OBB method (Oriented Bounding Boxes). Thanks to

these two methods, the object rendering is optimized

because the original object shape can be approached

with less voxels than with a simple uniform spatial

enumeration. The modeling is finer with OBB tree

than AABB tree for a same number of bounding

volumes. However, AABB tree uses less memory

storage than OBB tree for a same number of

bounding volumes. Indeed, an OBB is represented

by using 15 scalars (9 scalars for the orientation, 6

scalars for position and extent), whereas an AABB

only requires 6 scalars (for position and extent).

Moreover, to optimize the modeling of the 3D

object, these two methods suggest to reduce overlaps

between bounding boxes and to increase their filling

by the object, with the less possible boxes. This

optimization is expensive in processing time, so we

prefer using a uniform spatial enumeration or an

octree, because they are faster than AABB and OBB

methods.

Liu (Liu, 1988) and Hubbard (Hubbard, 1995)

propose to replace cubes by spheres in an octree to

form a spheres tree, because spheres accelerate

collision detection between objects. Later, Hubbard

(Hubbard, 1995) (Hubbard, 1996) and Bradshaw

(Bradshaw, 2004) suggest a finer modeling using

spheres tree thanks to an approximated medial-axis

of the 3D object, but this method is slower and more

complicated than an octree.

To further improve the use of spatial

enumeration, several methods of multiresolution

representations have been proposed. So, processing

and display times are adapted with the desired level

of detail. Among these methods, there are octree and

wavelet decomposition.

An octree can also be seen as a hierarchical

representation of 3D object. The maximum level of

subdivision of the octree defines the maximum level

of detail of a multiresolution representation. Boada

(Boada, 2001) defines a section in an octree that

determines the displayed nodes for a defined level of

detail. This method is extended to a n-tree by Ferley

(Ferley, 2002).

The second multiresolution method uses wavelet

decomposition. Wavelets are a mathematical tool for

representing functions hierarchically. In our case,

these functions are discrete 3D functions that define

a set of voxels. More information about wavelets

will be given in the section 2.1. Muraki (Muraki,

1992) (Muraki, 1993) shows the use of 3D Haar

wavelets to represent a 3D object. Pinnamaneni

(Pinnamaneni, 2002) builds a 3D Haar wavelet

decomposition from a sequence of 1D Haar wavelet

decomposition in each direction of the 3D voxels

grid. Wavelet decomposition allows to display a 3D

object faster according to the level of detail. It also

permits to drastically cut down the memory cost,

because high compression ratio can be achieved on

wavelets coefficients, especially if lossy

compression schemes are used.

The previously cited methods are about discrete

representation of 3D objects. Different methods have

already been proposed to sculpt these kinds of

objects.

Ayasse (Ayasse, 2001) performs sculpture

operations by the use of CSG (Constructive Solid

Geometry). Complex objects are created by

successive modifications of the material with a tool

according to simple operations such as difference,

union or intersection. However, the object and the

tool are represented by simple uniform spatial

enumerations. Moreover, voxels are limited to

binary values (full or empty). Ayasse proposes to

reduce the computation time for each sculpture

operation by using only the effective voxels of a

movement. This method can be useful because the

computation times are reduced. However, it doesn’t

use a multiresolution representation that could

improve the display performance or computation.

In the Kizamu project, Frisken (Frisken, 2001)

uses ADFs (Adaptively sampled Distance Fields) to

model and to sculpt the material. A 3D object is

sampled adaptively with a 3D grid according to the

details of the object. Each grid cell contains a scalar

specifying the minimum distance to the object

shape. This distance is signed to distinguish between

the inside and outside of the shape.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

416

To represent an object to be sculpted, Ferley

(Ferley, 2002) also uses distance fields, stored in a

“n-tree” hierarchical representation where the

sampling rate depends on object’s details. The tool is

an ellipsoid defined by an implicit function that is

discretized to perform sculpture actions on the

object.

Bærentzen (Bærentzen, 2002) proposes the

Level-Set method to deform the material. This

method stores distance fields around the exterior of a

3D object. The tool is a blob represented by an

implicit function.

Raffin (Raffin, 2004) proposes a model of virtual

sculpture based on a multiresolution representation:

the octree. The tools are defined as voxels sets, but

they remain parallel to the axis.

1.3 Original Contribution

The main contribution of this paper is to propose a

discrete multiresolution model for virtual sculpture.

We take benefit of levels of detail to accelerate

display, interaction and sculpture operations. As the

same model is used to represent both objects and

tools, a major advantage of our system over existing

methods is that the user can create his or her own

tools from a previous sculpture. Furthermore, we

provide solutions to problems inherent to the use of

discrete objects, such as computation cost, aliasing

and operations between discrete tools and objects.

The remainder of the paper is organized as

follows: in section 2, we describe our discrete

multiresolution model. In section 3, we present the

tools, with original solutions for computation cost,

aliasing and sculpture operations. Then, we conclude

in section 4 and present future work in section 5.

2 OUR MODEL

In a virtual sculpture project, we represent the 3D

objects to be sculpted as a discrete set of voxels to

easily handle subtraction or addition of material by

tools. However, a uniform spatial enumeration is

expensive in processing and display times. Thus, we

propose a multiresolution model based on 3D Haar

wavelets.

2.1 About Wavelets

On the following example, we explain Haar wavelet

decomposition on a 1D case. First, consider a

sequence of p values, where p is a power of two

(here, p = 4 = 2

[

]

9, 7, 3, 5X =

Then, by applying Haar wavelet transform, we

can represent this sequence in terms of a low-

resolution sequence X

and a set of detail

coefficients Y

[]

9735

,8,4

⎡⎤

⎢⎥

⎣⎦

[]

9735

,1,1

−−

=−

⎡⎤

⎢⎥

⎣⎦

So, by repeating these operations, we obtain

several sets of coefficients corresponding to

different levels of detail, as shown on the following

decomposition table:

level of detail

low-resolution

coefficients

detail

coefficients

0 [ 9 7 3 5 ]

1 [ 8 4 ] [ 1 -1 ]

2 [ 6 ] [ 2 ]

Thus, the higher the number of the level of

detail, the less detailed the sequence. The sequence

obtained by Haar wavelet decomposition has the

same size as the original sequence. Its coefficients

are the low-resolution coefficients of the last level of

detail and the different detail coefficients:

Original sequence: [ 9 7 3 5 ]

Final sequence: [6 2 1 -1]

The extraction of the original sequence from the

final sequence uses the inverse wavelet transform:

[

]

[

]

62,62 8,4X =+ −=

(

)()

[

]

[

]

81,81,4 1,4 1 9,7,3,5X =+ − +− −− =

2.2 Definition of our Model

Similarly, we can use this wavelet transform in a 3D

case. First, the 3D discrete object is defined by a

uniform spatial enumeration. Then, by using the

wavelet transform we build a hierarchical structure

that stores the coefficients of each level of detail of

this 3D object.

We use the hierarchical structure proposed by

Pinnamaneni [Pin02]. For each level of detail, the

1D Haar Wavelet transformation is applied in x-, y-

and z-direction successively (figure 1).

DISCRETE TOOLS FOR VIRTUAL SCULPTURE

417

LLH HLH

HHH

HHLH

HLLL

3D Image

LLL HLL

HHLLHL

Figure 1: 3D Haar wavelet decomposition.

For each transformation step, we obtain a bloc

‘L’ with low-resolution coefficients obtained by a

low-pass filter, and a bloc ‘H’ with detail

coefficients obtained by a high-pass filter.

The figure 2 shows a 3D Haar wavelet

decomposition for a sphere with 6 levels of detail.

Each voxel contains a density value coded on one

byte (from 0 for an empty voxel to 255 for a full

one).

Figure 2: 3D wavelet enumeration for a sphere in

128x128x128 with 6 levels of detail (from 0 to 5, from left

to right, and from top to bottom).

The building time (for wavelet decomposition of

the 3D image) and the extracting time (for extraction

of a level of detail from wavelet enumeration) do not

depend on the kind of 3D object. These times only

depend on the number of voxels of the initial

uniform spatial enumeration and on the desired

levels of detail of wavelet enumeration. Measured

times are reported on Table 1. Note that an

improvement will be described in section 2.3 to

reduce these times. The results given in this paper

have been obtained on a PC with an AMD 3GHz,

1GB of RAM and a NVIDIA Geforce FX 5200 with

128MB video memory.

Table 1: Building and extracting times for a 3D Haar

wavelet enumeration with a most detailed level of

128x128x128 voxels.

Extracting

Building

(5 levels)

Level 0

(128

)

Level 1

(64

)

Level 2

(32

)

Level 3

(16

)

0.6975 s 0.7529 s 0.0627 s 0.0019 s 0.0002 s

2.3 Display

We display this discrete object with the marching

cubes algorithm (Lorensen, 1987) that provides a

smooth surface instead of a set of blocky voxels.

During display, we take advantage of the

multiresolution nature of our model given by the 3D

wavelets to display the more appropriate level of

detail according to the situation (Distance between

the object and the point of view, needed frame rate).

Moreover, we implemented a data cache that

improves performances by managing the triangles

generated for each level of detail by the marching

cubes. Thus, there are two big advantages. First, it is

not necessary to extract a level of detail from the

wavelets if it is already present in the cache, thus

alleviating the computation times presented in

Table 1. Second, during sculpture actions, it is only

necessary to recompute the surface for the parts of

the object modified by the tool.

In our virtual sculpture system, we use this same

model to represent both objects and tools.

3 THE TOOLS

As stated in the introduction of this paper, the use of

discrete objects and discrete tools leads to problems

of computation time, aliasing and sculpture

operations. We will provide solutions to these three

problems in the following points.

3.1 Tools Orientation

In order to allow any orientation of a tool over the

object to be sculpted, we have to face the problem of

discrete rotation of the tool in its 3D matrix of

voxels. Note that we always apply the rotation to a

reference object, not to a previously rotated object,

because it would result in more and more

deteriorated object.

3.1.1 Computation of the Rotated Tool

Bounding Box

Before performing the rotation of this 3D image of

voxels, we have to determine its size after rotation.

We first compute the rotation of its 8 corners. The

bounding box of the 8 rotated corners gives the final

size of the image after rotation. Thus, we ensure that

the rotated tool will be totally enclosed in the final

bounding box.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

418

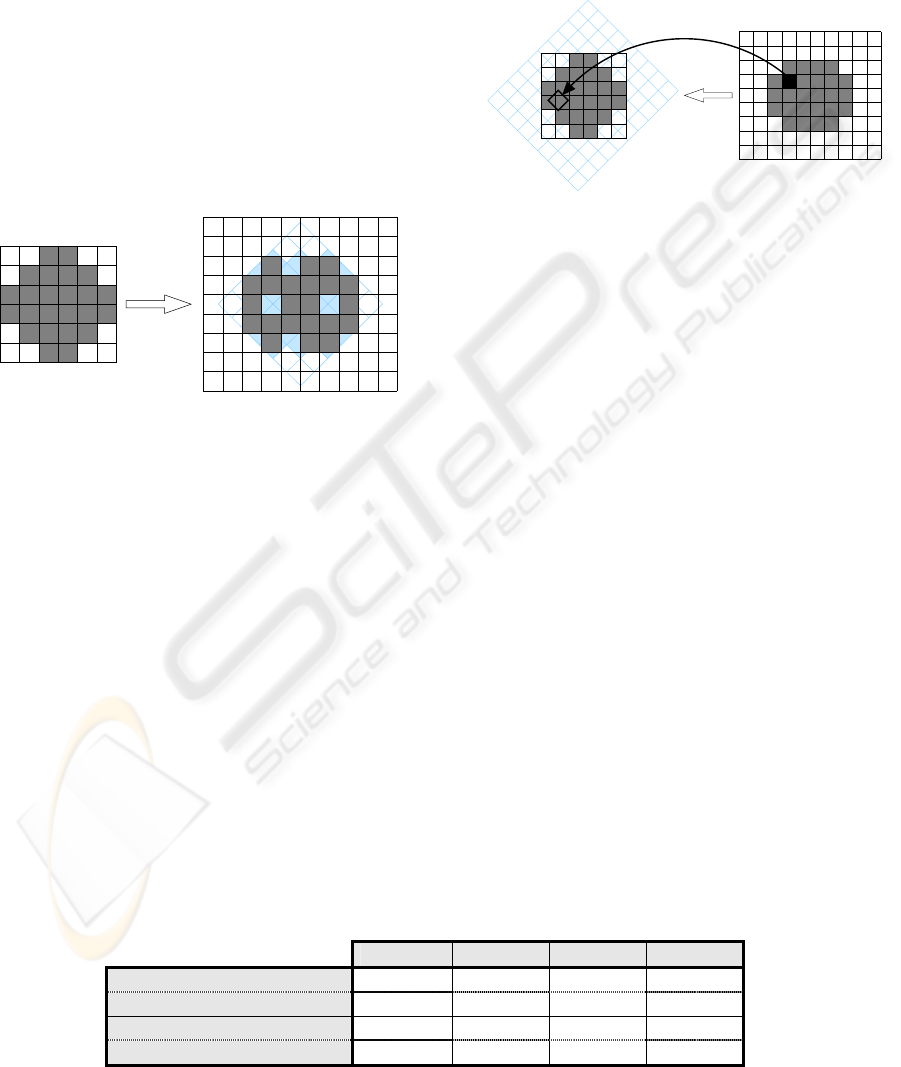
3.1.2 Direct Method

In order to perform the rotation of the 3D image of

voxels, the first idea would be to apply the rotation

to the voxels of the source image to fill the

destination image. Thus, for each voxel of the source

image, we multiply its position by the rotation

matrix, thus obtaining a rotated position. As the

coordinates of this position are real numbers, they

are then truncated to integers. The value of the

source voxel is then affected to the voxel at this

rotated position in the destination image.

However, as we can see on figure 3, this results

in holes in the final image as many voxels from the

source can be projected to the same voxel in the

destination due to truncation error to integers.

Consequently, a direct rotation of the source image

is inadequate.

Initial Image

Final Image

Rotation

Matrix

Figure 3: The use of the direct method to compute the

rotation of a discrete image results in holes in the final

image.

3.1.3 Inverse Method

The solution is to perform the inverse mapping. We

consider each voxel in the final image and map

backwards to find the closest voxel in the initial

image by applying the inverse rotation matrix. In

this way, every voxel in the final image is found,

without hole (figure 4).

However, there are still two problems:

− First, the computation time of this “brute force”

rotation is high, as we multiply each voxel

position of the final image by the inverse

rotation matrix (Of course, this one is only

computed once). Computation time increases

with the size of the 3D image, i.e. with the

number of voxels.

− Second, there is important aliasing in the final

image.zasing.

The aliasing problem will be tackled in the

following section. In order to reduce computation

time to allow real-time tool rotation, we propose an

optimised rotation method with three improvements

over the “brute force” method.

Matrix

Initial Image

Final Image

Inverse

Rotation

Figure 4: With the inverse rotation method, no hole is

obtained in the final image.

First, we do not compute the inverse

transformation for all the voxels of the final image,

but only for 4 voxels defining 3 orthogonal axes.

Positions of all other voxels are computed by simple

interpolations from these 4 positions (algorithm 1).

Computation times have been reported on table 2.

Moreover, comparisons between computation times

with brute force method and optimised method have

been reported on graph 1, for a tool in 16x16x16.

We can see that with this optimisation the rotation

time is cut down by 75% compared to the “brute

force” method. We can see that the computation

times depend on angle of rotation because the

number of voxels needed to store the rotated tool

changes with the angle.

Second, we drastically cut down the computation

time by only performing the rotation for the voxels

of the tool that are in contact with the object to be

sculpted. Indeed, this rotation is only required for

internal needs to perform sculpture operations. For

the display of the tool, we do not compute the

discrete rotation of the voxels, but we simply use

OpenGL rotation capabilities with the

glRotate() function. Thus, we can display tools

with good rendering quality, without distortion due

to discrete rotation.

Third, in order to reduce furthermore the

computation times, we store the already rotated

Table 2: Computation times obtained with different methods for rotation of a discrete tool for different resolutions

(averaged times for various rotation angles).

8x8x8 16x16x16 32x32x32 64x64x64

Brute force 0.1826 ms 1.321 ms 10.17 ms 82.3 ms

Optimised 0.0456 ms 0.322 ms 2.49 ms 18.1 ms

Brute force with antialiasing 0.2303 ms 1.628 ms 12.45 ms 102.1 ms

Optimised with antialiasing 0.0494 ms 0.351 ms 2.55 ms 18.7 ms

DISCRETE TOOLS FOR VIRTUAL SCULPTURE

419

voxels in a cache structure. Thus, we avoid to

compute them again when the contact area between

the tool and the object has changed. We only

compute the rotation of the voxels of the tool newly

entered in the area.

Algorithm 1: Discrete rotation of the tool.

P = voxel in final image

M = point in initial image

M = Inverse_Rotation(P)

b = (i,j,k) = final basis

B = (I,J,K) = initial basis

B = Inverse_Rotation(b)

dim = voxels number along an axis

in final image

FOR P.x=0 TO dim.X DO

FOR P.y=0 TO dim.Y DO

FOR P.z=0 TO dim.Z DO

// Get the value of the

// voxel M in initial image

P = GetValue(M)

// Next point M

M.x = M.x + K.x

M.y = M.y + K.y

M.z = M.z + K.z

END FOR

// Return along axis K in

// initial basis.

// M is incremented with J

M.x = -dim.Z * K.x + J.x

M.y = -dim.Z * K.y + J.y

M.z = -dim.Z * K.z + J.z

END FOR

// Return along axis J in

// initial basis.

// M is incremented with I

M.x = -dim.Y * J.x + I.x

M.y = -dim.Y * J.y + I.y

M.z = -dim.Y * J.z + I.z

END FOR

Please note that the computation times reported

on table 2, graph 1 and graph 2 are the times

observed in the worst cases, when all the voxels of

the tool have to be rotated (all voxels of the tool in

contact with the object and no voxel present in the

cache). In practical cases, the times are much lower.

0,5

1, 5

2,5

0 60 120 180 240 300 360

angles (degrees)

times (ms)

Graph 1: Comparison between computation times for

brute force method (dashed line) and optimised method

(solid line) for various rotation angles.

3.2 Antialiasing

Figure 5: A rotated cube without (a) and with antialiasing

by trilinear interpolation (b).

A major drawback of the rotation of a discrete image

is aliasing. The lower the image resolution, the more

important the aliasing (figure 5a).

0,5

1, 5

0 60 120 180 240 300 360

angles (degrees)

times (ms)

Graph 2: Comparison between computation times for

brute force method (dashed line) and optimised method

(solid line) with antialiasing for various rotation angles.

In order to reduce aliasing, we compute the value

of a rotated voxel from a trilinear interpolation of its

8 neighbours in the original image. Much better

results are obtained (figure 5b) to the price of

slightly higher computation times (On average,

+25% for the brute force rotation, +5% for the

optimised rotation as reported on Table 2). As for

graph1, we can see on graph 2 that the computation

times depend on angle of rotation.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

420

3.3 Sculpture Operations

Thanks to the representation of the material to be

sculpted as a set of volume elements, we can easily

handle sculpture actions such as subtraction or

addition of material. Other sculpture actions will be

studied in future work. A major advantage of our

method is that the tool used for virtual sculpture has

the same representation than the material. So, the

user can create his or her own tools to sculpt another

3D object.

Figure 6: Adding or subtracting material to an object with

a tool.

During the sculpture operations, a collision test is

first made between the bounding boxes of the tool

and the material. If there is a collision, the following

operations are performed:

− Find the voxels of the material and the tool

which are in the collision zone.

− Extract the value of each voxel of the tool in the

collision zone by using the discrete rotation.

− Find which voxel of the tool intersects which

voxel of the material in this zone.

If there is intersection between voxels of the

material and the tool in the collision zone, we

compute the filling percentage of the voxel of the

material by the one of the tool. The values of the

voxels of the material are then modified according to

the sculpture mode (illustrated in 2D on figure 6):

− In the “Adding material” mode, if the voxel of

the tool isn’t null, the filling percentage is added

to the value of the voxel of the material. If this

value becomes greater than 255, it is put to 255.

− In the “Subtracting material” mode, if the voxel

of the tool isn’t null, the filling percentage is

subtracted to the value of the voxel of the

material. If this value becomes negative, it is put

to 0.

For each level of detail, the triangulated surface

is rebuilt by marching cubes only for the modified

parts of the 3D object to improve the computation

time.

Examples of sculptures produced by our system are

shown on figures 7 and 8.

Figure 7: Chain with a ball, in 256x256x256, sculpted

with a spherical tool, a cubic tool and a ring tool in less

than 10 minutes.

Figure 8: Design of a new tool (a) using a ring tool and a

spherical tool. A more complicated object (b) sculpted in

less than 5 minutes using the previously designed tool.

4 CONCLUSION

We have presented in this paper a model for virtual

sculpture of 3D objects with tools. Both objects and

tools are represented by 3D Haar wavelets. This

multiresolution model permits to avoid speed and

memory issues inherent to a representation based on

voxels. The discrete representation as volume

elements allows to handle easily sculpture

operations such as subtraction or addition of

DISCRETE TOOLS FOR VIRTUAL SCULPTURE

421

material. Unlike other existing virtual sculpture

methods, a major advantage of our model is that the

tools can freely be created by the user.

In order to allow any orientation of a tool over

the object to be sculpted, we have developed an

algorithm of discrete rotation of the tool in its 3D

matrix of voxels. In order to enhance real-time

performance, this algorithm is applied only for the

voxels of the tool that are in contact with the object

to be sculpted. Aliasing problems inherent to

discrete rotation are reduced thanks to a trilinear

interpolation to the cost of slightly higher

computation time.

To verify the applicability of our sculpting

system, we have conducted many sculpting sessions

which have resulted in numerous interesting

sculptures. Some sculptures examples are shown on

figures 7 and 8, and several other examples can be

seen on http://www.iut-arles.up.univ-mrs.fr/thon/.

5 FUTURE WORK

Many improvements of our sculpture system are

possible, by investigating open issues such as

interaction with the object or computation time.

Concerning interaction, we plan to improve the

realism of sculpture actions, by adding parameters to

the voxels to imitate physical behaviour. Enhanced

sculpture actions will then be possible.

Interactive computation times will always be a

challenging issue. In order to accelerate the

sculpture actions, we plan to take more advantage of

the levels of detail of the 3D Haar wavelet. We will

also investigate the use of graphics hardware to

speed up many parts of our system, such as voxels

rotation or sculpture actions.

REFERENCES

Ayasse, J., Müller, H., 2001. Interactive Manipulation of

Voxel Volumes with Free-formed Voxel Tools. In

Proceedings of the Vision Modeling and Visualization

Conference 2001, 359-366.

Bærentzen, J.A., Christensen, N.J., 2002. Volume

sculpting using the Level-Set method. In Shape

Modelling International 2002. IEEE Computer

Society, 175-182.

Bergen, G.V.D., 1997. Efficient collision detection of

complex deformable models using AABB trees. In

Journal of Graphic Tools, 2(4), 1-13.

Boada, I., Navazo, I., Scopigno, R., 2001. Multiresolution

volume visualization with a texture-based octree. In

Visual Computer, 17, 185-197.

Bradshaw, G., O’Sullivan, C., 2004. Adaptive medial-axis

approximation for sphere-tree construction. In ACM

Transactions on Graphics, 23(1), 1-26.

Ferley, E., 2002. Sculpture virtuelle. Ph.D. thesis, Institut

National Polytechnique de Grenoble.

Frisken, S.F., Perry, R.N., 2001. Kizamu: a system for

sculpting digital characters. In Proceedings of ACM

SIGGRAPH 2001, 47-56.

Gottschalk, S., Lin, M.C., Manocha D., 1996. OBB-Tree:

A hierarchical structure for rapid interference

detection. In Proceedings of ACM SIGGRAPH’96,

171-180.

Hubbard, P., 1995. Collision detection for interactive

graphics applications. Ph.D. Thesis, Dept. of

Computer Science, Brown University.

Hubbard, P., 1996. Approximating polyhedra with spheres

for time-critical collision detection. In ACM

Transactions on Graphics, 15(3), 179-210.

Libes, D., 1991. Modeling dynamic surfaces with octrees.

In Computer & Graphics, 15(3).

Liu, Y., Noborio, J., Arimoto, S., 1988. Hierarchical

sphere model (HSM) and its application for checking

an interference between moving robots. In

Proceedings of the IEEE International Workshop on

Intelligent Robots and Systems, 801-806.

Lorensen, W.E., Cline, H.E., 1987. Marching Cubes: a

high-resolution 3D surface construction algorithm. In

Computer Graphics, 21(4), 163-169.

Muraki, S., 1992. Approximation and rendering of volume

data using wavelet transforms. In Proceedings of

Visualization ’92, Boston, 21-28.

Muraki, S., 1993. Volume data and wavelet transforms. In

IEEE Computer Graphics and Applications, 13(4), 50-

56.

Pinnamaneni, P., Meyer, J., Saladi, S., 2002. Remote

transformation and local 3-D reconstruction and

visualization of biomedical data sets in Java3D. In

Proceedings of Electronic Imaging Science &

Technology Visualization and Data Analysis

Conference, San Jose, CA, 44-54.

Raffin, R., Gesquière, G., Remy, E., Thon, S., 2004.

VirSculpt: a virtual sculpting environment. In

GraphiCon '04 Proceedings, 184-187.

Szeliski, R., Tonnesen, D., 1992. Surface modeling with

oriented particle systems. In Computer Graphics,

26(2), 185-194.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

422