INTERACTION BETWEEN WATER AND

DYNAMIC SOFT BODIES

Tatiana Alexandrova, Olivier Terraz, Djamchid Ghazanfarpour

XLIM Laboratory UMR CNRS 6172, University of Limoges,83 rue d’Isle,87000 Limoges, France

Keywords: liquid animation, movement simulation, dynamic soft body, Lattice-Boltzmann method.

Abstract: The water animation by moving soft bodies, changing their shapes, is the subject of the present work. The

mechanism of movement transformation from a body to a liquid is elaborated on the basis of Lattice-

Boltzmann method of fluid modeling. The use of boundary conditions, destined to perform this

transformation visually realistic and computationally quite inexpensive, is one of the main innovations of

our approach. The model is applied to the jellyfish propulsion water.

1 INTRODUCTION

The subject of this work is a physically based

modeling of a liquid animation caused by a soft

dynamic body movement. In computer graphics,

physical based models have an important advantage

compared to empiric ones. They make the scene

evolve automatically and do not require the user

intervention for each animation step. Once the

relations and laws of interaction among objects

and/or medium are given, the correctly produced

system automatically simulates the behavior of the

whole scene. This gives essential increasing of

computational time. Recent physically based models

(Guendelman, Selle, Losasso, Fedkiw, 2005),

(Muller, Solenthaler, Keiser, Gross, 2005) are

developed in order to maximally reduce the

calculation time and to present visual plausibility,

keeping the details of a real world animation.

The model presented in this paper proposes a

quite simple way of transforming body motion to

liquid motion. The special, easy to apply boundary

conditions are elaborated in application to the

Lattice Boltzmann method for this purpose. The

model is applied to underwater scenes with

swimming jellyfish. The simulations of jellyfish

movement and its interaction with particles in water

and with algae are performed.

The paper is composed as follows. In the second

part, the liquid animation models are discussed. The

third part is devoted to the transformation of soft

body movement to surrounding water and

consequently to neighboring objects. In this part, we

can find the main innovation of this work: the

boundary conditions for moving soft bodies. The

fourth part presents the results obtained by this

method. The last section concerns conclusions and

future work.

2 ANIMATION OF LIQUIDS

In this section we give a brief review of liquid

modeling. There are the fluid dynamics methods,

simplified to satisfy the needs of computer graphics.

Computational fluid dynamics proposes a variety

of tools for fluid motion modeling, but it demands

special skills and resists external control. In addition,

it is very time consuming. In order to be applied in

computer graphics, simplified physically based

approaches were intensively developed during recent

years. To introduce first branch, one can refer to

(Foster, Metaxas, 1996), (Stam, 1999), (Foster,

Fedkiw, R., 2001). Visual fidelity is the main goal of

these models. These methods solve the Navier-

Stokes equations on a discrete voxel grid that causes

decreasing the time step or refinement of a grid

when the boundary geometry is complex.

There are several problems already considered in

this branch of liquid modeling; the models were

essentially improved compared to the first ones. In

(Genevaux, Habibi, Dischler, 2003) the fluid-solid

interaction was explored; the method is based

mainly on the definition of a coupling force between

384

Alexandrova T., Terraz O. and Ghazanfarpour D. (2006).

INTERACTION BETWEEN WATER AND DYNAMIC SOFT BODIES.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 384-391

DOI: 10.5220/0001357003840391

 SciTePress

the solids and the fluid. In (Guendelman, Selle,

Losasso, Fedkiw, 2005) the method for water - cloth

interaction, well suiting also to water - air and solid -

fluid interface, is given. The rigid body - fluid

interplay is presented by a Rigid-Fluid method in

(Carlson, Mucha, Turk, 2004).

Recently, the Smoothed Particle Hydrodynamics

method was presented in application to fluid - fluid

interaction, water pouring into a glass and

interaction of fluid with deformable solids (Muller,

Solenthaler, Keiser, Gross, 2005), (Muller,

Charypar, Gross, 2003), (Muller, Schrim, Teschner,

Heidelberger, Gross, 2004).

The other direction in flow simulation is the

Lattice-Boltzmann method (LBM) (Chen, Doolean,

1998), (Wei Li, Zhe Fan, Xiaoming Wei, Arie

Kaufman, 2003). It gives a microscopic

representation of a fluid as a set of microscopic

particles. The method is derived from the Boltzmann

equation from the kinetic theory of gases. Almost all

Lattice-Boltzmann equations simulate compressible

fluids with some finite sound speed c

. However the

computed solutions are expected to converge to

incompressible limit, when the liquid speed |

| is

sufficiently small compared to the sound speed c

(Mach number

0/ →=

cuM

Let us consider the principles of LBM. The

liquid is represented by a finite regular grid and by a

set of a packet distribution values

{

}

f for each cell

of a grid. Each packet distribution value

corresponds to the velocity direction vector

shooting from a node to its neighbor. A pair

(

f ,

) indicates how many particles

f in the

cell have the velocity direction

It is supposed that there always exists a local

equilibrium particle distribution

f dependent only

on the density

, and on the local fluid velocity

The LBM updates the packet distribution values at

each cell based on two rules:

collision:

qiqi

new

tXftXf Ω=− ),(),(

(1)

propagation:

),()1,( tXfteXf

new

qiqiqi

=++

(2)

where X is the coordinate in R

, and

Ω is the

general collision operator. Since the components of

can only be chosen from {-1, 0, 1}, the

propagation is local.

Collision describes the redistribution of packets

at each local node. Propagation means the packet

distributions move to the nearest neighbor along the

velocity direction.

The density and velocity are calculated for each

cell from the packet distributions as follows (

Wei Li,

Zhe Fan, Xiaoming Wei, Arie Kaufman, 2003):

∑

Mass and momentum are conserved locally.

Then, the collision step (with commonly used BGK

collision term (Bhatnagar, Gross, Krook, 1954)) is:

()

),(),(

),(),( vftXftXfvf

qiqiqi

new

−−=−

where τ is a relaxation time (timescale for which

every variable relaxes towards equilibrium), which

determines the viscosity of the flow,

is the

local equilibrium distribution function.

A great advantage of this method is that it

supports dynamic boundary conditions. For more

details see (Chen, Doolean, 1998), (Wei Li, Zhe Fan,

Xiaoming Wei, Arie Kaufman, 2003).

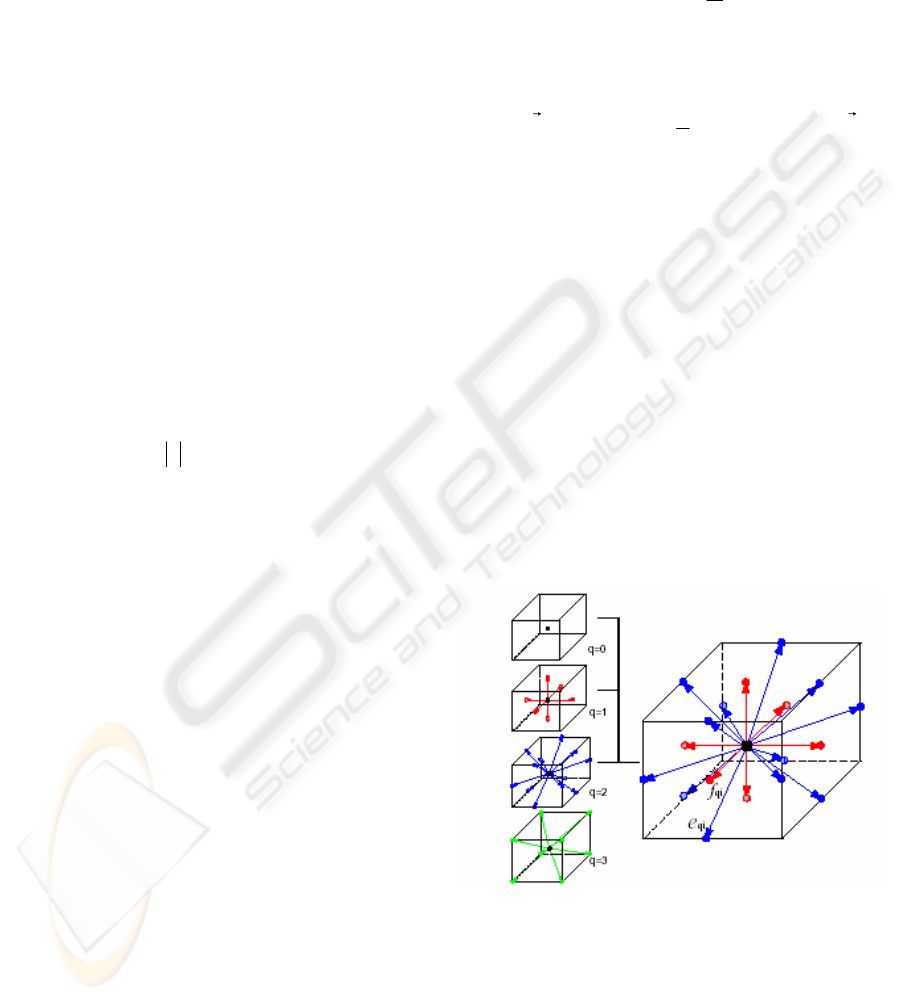
There exist the following usual models with a

rest particle for 3D space (see Fig.1): D3Q15 (fifteen

velocities), D3Q19 (nineteen velocities), D3Q27

(twenty seven velocities) (Renwei Mei, Wei Shyy,

Dazhi Yu, Li-Shi Luo, 2002). A minor variation of

those models is to remove the rest particles from the

discrete velocity set; the resulting models are known

as the D3Q14, D3Q18, and D3Q26 models,

respectively. The LBM with a rest particle generally

have better computational stability.

Figure 1: 3D lattice geometry. On the left side there are

presented the four sub-lattices that are defined in a 3D

lattice. On the right side is the combination of sub-lattices

0, 1, and 2 (19 packets) (Wei Li, Zhe Fan, Xiaoming Wei,

Arie Kaufman, 2003).

In the present work the D3Q15 model is taken,

the simplest model for 3D space, in our case it suits

well due to the smoothness of the movement and the

simplicity of the scene objects:

INTERACTION BETWEEN WATER AND DYNAMIC SOFT BODIES

385

⎪

⎩

⎪

⎨

⎧

=±±±

IIgroupi

Igroupi

particleresti

14,...,7)1,1,1(

6,...,1)1,0,0(),0,1,0(),0,0,1(

,0)0,0,0(

3 TRANSFORMATION OF BODY

MOVEMENT TO A LIQUID

MOVEMENT

The movement of the dynamic body, once properly

transferred, animates the liquid and neighboring soft

bodies, the passive and the active ones. An example

is the swimming jellyfish, which can transfer the

motion to other jellyfishes and algae surrounding it.

Let us suppose that the parameters of dynamic

body surface, such as coordinates and velocities of

the control points, are known at each time step. The

most important part in a water animation by a body

is the interaction, where the movement of a dynamic

surface should be properly transferred to the lattice

cells. Here we are restricted to one-way

transformation of movement, which means that the

body is not influenced by a liquid but acts as a motor

of a motion. The full interaction, the reciprocal

influence of the body and the liquid complicates the

problem.

The transformation of the movement is done

with assigning local surface velocities to the

boundary lattice cells touching the jellyfish surface

and their subsequent influence on the other cells. At

the starting point at time

0=t

the uniform

equilibrium distribution with velocity

and

constant water density is assigned to all lattice cells.

The coordinate of a unit cell is a vector, formed

by the minimal integer numbers of cell points

coordinates. So, the point (-5.3, 2.6, 0.1) belongs to

the cell with coordinates (-6, 2, 0).

Further, we consider the swimming jellyfish as

an example. The movement of the jellyfish suits to

our aim of deforming body – liquid interaction

simulation. The movement consists of contraction

and relaxation of the bell forming the body, so the

jellyfish opens and closes its bell.

Now we have to explain briefly the model of

jellyfish body and its animation model made here.

The jellyfish is presented as a NURBS surface with

axial symmetry (see Fig. 2). For the deformation a

dynamic particle system is used; the particles are

shown in the figure with points. The particle system

is a set of unit-masses, where the forces are applied.

The particles are placed in 96 CVs, the control

points, which control the shape of the surface.

For a better implementation of the deformation

system in the present model, the particles were

placed in CVs and then the shape of the surface was

modified. Particles positions at the low part of

jellyfish do not correspond to CV positions, but still

keep connection; the particle translations are applied

to corresponding CVs.

Jellyfish contractions are simulated by 10

axisymmetric mass-spring systems. Each spring acts

accordingly to its rigidity, a length at rest, and

weights of the particles at the ends. At the beginning

the springs are supposed to be stretched, that gives a

contraction. At the relaxation phase, the springs are

supposed to be compressed. For simplicity, the

properties of the springs are changed at certain time

points during scene evaluation in order to alternate

contractions and relaxations.

Figure 2: Jellyfish model with particle system and mass-

spring system.

As we know the coordinates of the control points

of the body, these 3D coordinates determine the

corresponding boundary cells; the velocities of the

control points allow the calculation of the packet

distributions for LBM. They can be taken as the

equilibrium distributions with the local surface

velocity and a constant water density for all cells, as

the water is a non-compressible liquid. Linear

interpolation is applied to calculate coordinates and

velocities of the cells in between the control points.

The lattice is finite and the boundary conditions

are to be set for the boundaries of the lattice, as well

as for the boundaries of the body.

3.1 Boundary Conditions on the

Lattice Border

Boundary conditions in the LBM may take several

forms (Wei Li, Zhe Fan, Xiaoming Wei, Arie

Kaufman, 2003). The conditions that can be applied

to the border of the lattice include periodic boundary

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

386

and outflow boundary. For periodic boundary, the

outgoing distributions wrap around and re-enter the

lattice from the other side. For outflow boundary,

distributions propagating outside the lattice are

simply discarded. However, boundary cells also

have some distributions propagating inwards from

fictitious cells just outside the boundary.

3.2 Boundary Conditions on the

Body

Now let us consider obstacle boundaries, which

should be set for objects inside the lattice. The “no-

slip” boundary condition requires that the tangential

component of the fluid velocity along the boundary

be zero. The simple implementation is a bounce-

back rule. The outgoing distribution, facing the

boundary, re-enters the lattice at the same cell, but

associated with the opposite velocity.

In (Wei Li, Zhe Fan, Xiaoming Wei, Arie

Kaufman, 2003) improved boundary conditions are

applied to complex geometries and moving

boundaries. They are represented as a complex

function including neighbor cell distributions,

velocity of the local surface, proportional distances

to the cell nodes (coordinate points) and surrounding

water velocities.

In the present work the moving boundaries are

treated in different manner. The main purpose of

proposed boundaries is to transfer the movement

from object to water independently of surrounding

water velocities. This is the main distinction of our

method. The boundary cells are, in some way, the

fictitious cells. They affect the other lattice cells, but

are not affected by other cells. The properties of

these cells depend totally on the local surface

velocity. The velocity distributions in these cells are

set to the equilibrium values. The aim is to transfer

the object-in-water motion properly and in a simple

manner. The method proposed, uses the bounce-

back rule in combination with the interaction with

the fictitious boundary cells.

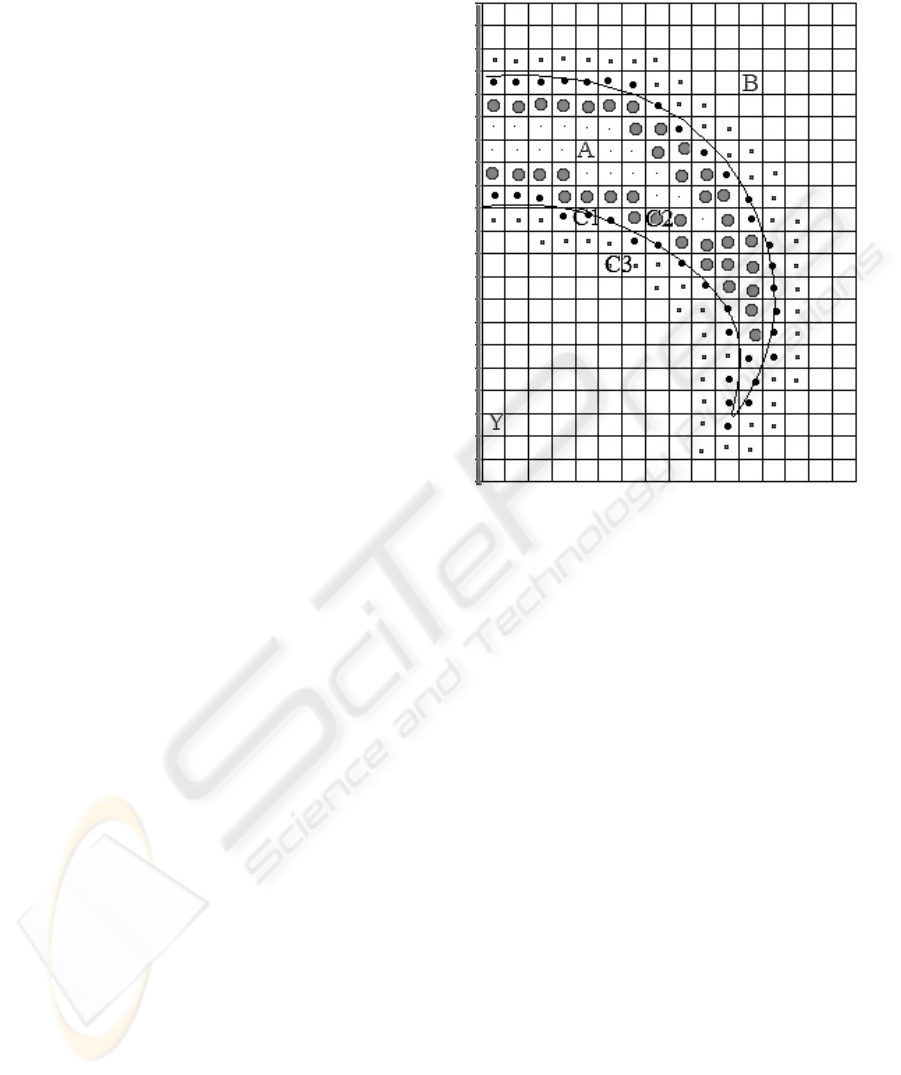
The lattice cells are separated in three groups,

see Fig.3. The first one (group A) is the group of

body inner cells. Inner cells mean the cells, which

stay inside the body as well as all of its neighbors.

These cells are passive and the distributions for them

are not calculated, they keep zero.

The second group (group B) includes water cells.

These are the cells, which are the cells of water as

well as all of its neighbors. The velocities of these

cells are calculated according to the standard

procedure in two steps: collision and streaming.

The third group (group C) is the boundary and

pre-boundary cells. This group is the most important

and is again divided into three groups:

Figure 3: Groups of lattice cells: A are the inner cells, B

are the water cells, C1, C2, C3 are the boundary cells.

1. boundary cells (group C1)

2. inner cells of the body which have at least

one boundary cell as a neighbor (group C2)

3. water cells which have at least one

boundary cell as a neighbor (group C3).

Further, we will discuss group C and its under-

groups. The cells of the first group, C1, get the

distributions

),(

loc

νρ

depending on local surface

velocity. The remaining two groups are responsible

for proper transferring of the movement.

Let us consider group C2, the inner cells. Since

we use linear interpolation to find the water cells

intersecting with body surface in between the control

points of dynamic system, it is important to find all

the cells having exchanges with the outside cells.

They are all inner cells having, at least, one C1

neighbor. In the present model their distributions are

set as average distributions of surrounding boundary

cells C1 (inner cells A are not taken into account).

The pre-boundary cells of group C3 get the

incoming distributions from C1 and C2 at a collision

step. But their own distributions, in directions to

boundary cells C1, change the direction for opposite

and re-enter to the cell. So, at the streaming step the

pre-boundary cells C3 get the incoming distributions

from the water cells B, from boundary cells C1, C2,

and, in addition, some of their own distributions are

INTERACTION BETWEEN WATER AND DYNAMIC SOFT BODIES

387

returned as they meet a wall (body surface). During

the evaluation of the dynamic system the lattice cells

change the status and pass from one group to

another.

The time step and the lattice size should be

properly chosen because the system can become

unstable. In the LBM the indication of instability of

a solution is the appearance of negative values of

equilibrium distributions at the collision step.

Physically, the model described above is not

accurate because mass is not strictly conserved. On

the other hand, the deviation is little and the method

is simple. The important feature of Lattice-

Boltzmann Method, the support of moving

boundaries, is used here and the movement issuing

from the object is successfully transferred to the

water space.

3.3 Jellyfish Propagation in a Water

Space

One more advantage can be gained from the

proposed application of the Lattice-Boltzmann

Model, the body propagation in liquid. Having

known the velocities of boundary cells, we know,

roughly speaking, the forces with which the body

acts on the liquid in these cells.

The propagation can be calculated based on the

momentum conservation law at the interaction of

two bodies having masses m

, m

and velocities v

correspondingly, m

In the case of a jellyfish swimming, a strong

simplification can be done. According to a

biological model, the jellyfish propagation is

generated by a cylindrical jet of water from the bell

cavity. Approximately, one can consider the two-

object system: the jellyfish and the cavity water; see

Fig.4.

Water

Jellyfish

Figure 4: Two-object system: the jellyfish and the bell

cavity water.

Here it does not matter what to consider, masses

or volumes, as the water and jellyfish densities are

almost equal. We know the volume of pushed water,

at each step it can be approximated as a sum over

boundary cells C1:

tlvV

cell

∆=∆

∑

here v

is the cell velocity, l

cell

is the cell size, ∆t is

the time step. Having this change of volume, we can

calculate the height of a column of water pushed by

jellyfish. The base of the column is taken as a circle

with the jellyfish aperture radius R

. The height of

the column is

∆

the velocity of the cavity

water is approximately taken as

∆

≈

. Now the

movement conservation law is used. Considering the

volumes in place of masses,

vv =

is the

jellyfish velocity at the current step, where

RaV

⋅=

is the approximate cavity water

volume, and the jellyfish volume V

is approximately

a sum of all inner cells (group A + group C2). The

jellyfish transition is calculated as

tvl

∆=∆ .

This model is non-correctly physically based

during jellyfish opening, but gives visually pleasing

results.

4 RESULTS

In this section we present the results of our model

application to underwater virtual words. Scenes are

modeled in Maya 6.0. A plug-in calculating the

velocity field in water, generated by a jellyfish

swimming is written in Maya API.

Let us consider the general parameters of the

scenes. In Fig.5 the jellyfish, the dynamic body, is

presented in the scene and the size of the lattice is

shown. The jellyfish is oriented normally to the

ground, but the orientation axis can be chosen

differently. It also can be changed during the

animation simulation as a function of some factor(s).

The bell diameter of relaxed jellyfish is about 40 cm,

and the field lattice cube size is 80 cm. In the present

results the size of lattice cells is 2 cm. The lattice

size is enough for movement transition to the

environment, and the values of cell velocities near

the lattice borders are almost negligible. These

parameters allow a frame rate about 1,1 frames per

second (cell size 2 cm) and 0,43 frames per second

(cell size 1 cm) on Intel Celeron 2.8GHz with 512

Mb RAM. It is not a real time simulation but an

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

388

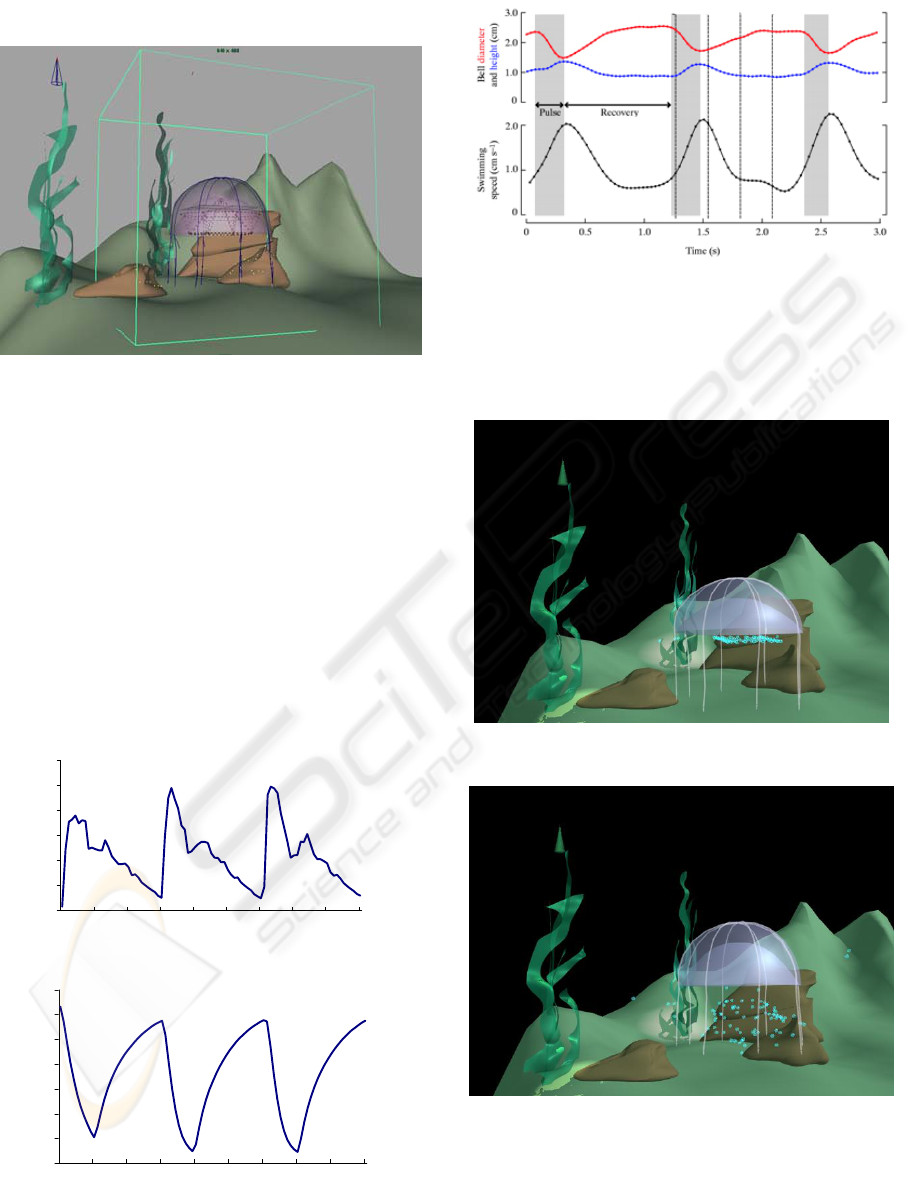
interactive time, where the evolution of the scene

can be followed.

Figure 5: The size of the lattice in comparison with the

scene.

The general character of the jellyfish propulsion

in water is presented in Fig.6, where the velocity of

the jellyfish and its aperture diameter are shown.

Comparing these data with the biological data

(

McHenry and Jed 2003) in Fig.7, the similarity of

movement character is to be pointed. The velocity of

jellyfish propulsion in our model depends on the

lattice cell size, which gives more or less precision

in calculation of a pushed water volume. Using

constant coefficients in the model allow regulation

of the jelly propulsion velocity according to

biological data or a desired movement.

(a)

0,2

0,4

0,6

0,8

1,2

0 8 17 25 33 42 50 58 67 75

time, s

propulsion velocity, cm/s

(b)

37,5

38,5

39,5

40,5

0 8 17 25 33 42 50 58 67 75

time, s

velocity, cm/s

Figure 6: The jellyfish propulsion velocity (a) and the bell

diameter (b) in dependence of time.

Figure 7: Representative kinematics of swimming in

jellyfish Aurelia aurita,

(McHenry and Jed 2003).

Further more, let us consider two scenes

animated by jellyfish movement. In the first scene,

the jellyfish make the particles move in the water,

presented as small spheres.

Figure 8 (a): Particles animated by jellyfish movement,

frame = 1.

Figure 8 (b): Particles animated by jellyfish movement,

frame = 400.

In Fig.8, four screenshots are given at frames: a) 1,

b) 400, c) 1400, d) 2000, the video is joined to the

article and available on http://www.msi.unilim.fr/

basilic/Publications/2006/ATG06. The ordered

INTERACTION BETWEEN WATER AND DYNAMIC SOFT BODIES

389

Figure 8 (c): Particles animated by jellyfish movement,

frame = 1400.

Figure 8 (d): Particles animated by jellyfish movement,

frame = 2000.

group of particles is intermixed by water flow.

Water movement also influences the tentacles. The

behavior of influenced objects looks quite natural.

In Fig.9, four screenshots from the underwater

scene with plants and some particles, placed in the

water, are shown; the video is joined to the article

and available on http://www.msi.unilim.fr/basilic

/Publications/2006/ATG06. The movement of the

green plants closest to the jellyfish can be easily

seen. In the underwater scene also appears the task

of a proper modeling of influenced objects. The

particle systems are well suited for this. Here, for

example, the green plants are modeled as particle

systems with particles placed in control points and

each particle is connected by springs with the closest

ones. Generally, this model should be complicated,

mostly by increasing the number of springs. In this

scene the simulation is visually pleasing and gives a

realistic impression of water flow pushing the plants.

Figure 9 (a): Underwater scene animated by jellyfish

movement, frame = 1.

Figure 9 (b): Underwater scene animated by jellyfish

movement, frame = 400.

Figure 9 (c): Underwater scene animated by jellyfish

movement, frame = 1400.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

390

Figure 9 (d): Underwater scene animated by jellyfish

movement, frame = 2000.

5 CONCLUSIONS AND FUTURE

WORK

In this paper we presented a simplified physical

model, based on the Lattice-Boltzmann method, for

the simulation of a movement transformation from a

dynamic soft body to a liquid. It is applied to a

jellyfish in underwater scenes. The field is realized

as finite lattice surrounding a jellyfish.

The special boundary conditions on the body

surface are elaborated for this task. They are devoted

to the aim of visually realistic presentation of the

body motion transferring to the environment.

Attention is also paid to the simplicity of the model.

Compared to previous work in this domain, the

following points should be mentioned:

• The special boundary on the body surface,

which depends only on the local properties of

the surface. Independence of the boundary cells

from the rest lattice cells allows taking into

account the body as a generator of the motion.

• The modeling of body propagation in the

water.

In a future work, the implementation of body

trajectory changes, in order to avoid obstacles, can

be considered. This can be done as a function of an

obstacle bounding box coordinates and a body

bounding box coordinates. Some minimum distance

can be presented and, if needed, the correction

vector may be added to jellyfish transition at each

time step to keep this distance. Also, the full

interaction can be considered, the reciprocal

influence of the body and the liquid.

As a disadvantage, we can mention the possible

instability of the solution that is usual for liquid

modeling. The time step, the cell size, as well as the

coefficients for the LBM model should be properly

set in order to avoid instabilities.

REFERENCES

Guendelman, E., Selle, A., Losasso, F., Fedkiw, R.,

(2005). Coupling Water and Smoke to Thin

Deformable and Rigid shells. ACM Transactions on

Graphics 24(3)

, 973-981, (SIGGRAPH 2005).

Muller, M., Solenthaler, B., Keiser, R., Gross, M., (2005).

Particle-Based Fluid-Fluid Interaction.

Eurographics/ACM SIGGRAPH Symposium on

Computer Animation

, 1-7.

Foster, N., Metaxas, D., (1996). Realistic Animation of

Liquids. Graphical Models and Image Processing 58,

471-483.

Stam, J., 1999. Stable Fluids. ACM SIGGRAPH 99, 121-

128.

Foster, N., Fedkiw, R., (2001). Practical Animation of

Fluids.

Proceedings of SIGGRAPH, 23-30.

Genevaux, O., Habibi, A., Dischler, J., (2003). Simulating

Fluid-Solid Interaction. Graphics Interface, 31-38.

CIPS, Canadian Human-Computer Communication

Society, A K Peters, ISBN 1-56881-207-8, ISSN

0713-5424.

Carlson, M., Mucha, P., Turk, G., (2004). Rigid Fluid:

Animating the Interplay Between Rigid Bodies and

Fluid. ACM Trans. Graph. 23, 3, 377-384.

Muller, M., Charypar, D., Gross M., (2003). Particle-

Based Fluid Simulation for Interactive Application.

Proceedings of 2003 ACM SIGGRAPH Symposium on

Computer Animation

, 154-159.

Muller, M., Schrim, S., Teschner, M., Heidelberger, B.,

Gross, M., (2004). Interaction of Fluids with

Deformable Solids.

Journal of Computer Animation

and Virtual Worlds (CAVW) 15, 3-4

, 159-171.

Chen, S., Doolean, G., D., (1998). Lattice-Boltzmann

Method for Fluid Flows,

Ann. Rev. Fluid Mech., 30,

329-364.

Wei Li, Zhe Fan, Xiaoming Wei, Arie Kaufman, (2003,

Nov.). GPU-Based Flow Simulation with Complex

Boundaries Technical Report 031105, Computer

Science Department, SUNY at Stony Brook

(http://www.cs.sunysb.edu/~vislab/projects/amorphou

s/WeiWeb/hardwareLBM.htm)

Bhatnagar, P., L., Gross, E., P., Krook, M., (1954). A

model for collision processes in gases. I: small

amplitude processes in charged and neutral one-

component system. Phys. Rev. 94, 511–525.

Renwei Mei, Wei Shyy, Dazhi Yu, Li-Shi Luo, (2002).

Lattice Boltzmann Method for 3-D Flows with Curved

Boundary, NASA/CR-2002-211657 ICASE Report No.

2002-17.

McHenry, M., Jed, J., 2003. The ontogenetic scaling of

hydrodynamics and swimming performance in.

jellyfish (Aurelia aurita).

The Journal of Experimental

Biology

,(http://jeb.biologists.org/cgi/content/abstract/2

06/22/4125)

INTERACTION BETWEEN WATER AND DYNAMIC SOFT BODIES

391