REALISTIC SIMULATION OF OCEAN SURFACE

USING WAVE SPECTRA

Jocelyn Fr

echot

LaBRI - Laboratoire bordelais de recherche en informatique

Domaine universitaire, 351 cours de la Lib

eration, 33405 Talence CEDEX, France

Keywords:

Natural phenomena, realistic ocean waves, procedural animation, parametric energy spectra.

Abstract:

We present a method to simulate ocean surfaces away from the coast, with correct statistical wave height and

direction distributions. By using classical oceanographic parametric wave spectra, our results ﬁt real world

measurements, without depending on them. Since wave spectra are independent of the ocean model, Gerstner

parametric equations and Fourier transform method can be used with them. Moreover, since they are simple to

use and need very few parameters, they allow easy production of ocean surface animations usable in movies

and games. We explain how to accurately sample them, to achieve oceanic waves in deep water according to

given wind parameters, in a realistic way.

1 INTRODUCTION

The reproductions of many natural phenomena is still

an open problem in Computer Graphics. In particular,

the realistic simulation of oceanic surfaces continues

to be of great interest. Many ﬁelds of activity rely on

it: virtual reality, movies and games, but also sailing

(Cieutat et al., 2001) and oceanographic simulations,

among others.

While beautiful pictures and animations such as

wave refraction (Gonzato and le Sa

ec, 2000) (Gamito

and Musgrave, 2002) are produced, there is still a

need for oceanic scenes with realistic wave features.

Models based on ﬂuid mechanics equations (Enright

et al., 2002) (Mihalef et al., 2004) should give the

more realistic results, but are inadequate for large

oceanic surfaces.

For twenty years, procedural models for wave rep-

resentation in Computer Graphics have been devel-

oped and improved (Iglesias, 2004). The Gerst-

ner parametric equations and their Fourier transform

rewriting are well known by the oceanographic com-

munity. Based on the linear wave theory, they allow

representation of natural wave shapes and moves in

deep water above the capillary size. As they not de-

scribe any net mass transport, they are limited to non-

breaking waves and to scenes without violent storms.

Wave height measurement data allow to simulate a

given sea state. In the more general case, oceanic sur-

face statistics are taken in account by the use of para-

metric wave spectra. For given wind parameters, they

indicate the distribution of wave energy as a function

of frequency. However, none of the existing methods

are able to correctly reproduce sea states described by

these spectra.

In this paper, we explain how wave spectra are

related to oceanic surface energy and we detail a

method to deduce wave heights from it. We propose

a solution for optimal spectrum sampling, suitable

for parametric and Fourier transform models. This

method enables the accurate simulation of oceanic

surface. Users can easily produce realistic wave ani-

mations, with respect to supplied weather conditions.

The structure of this paper is as follows. Section 2

summarizes ocean models for Computer Graphics. In

section 3, we detail our method and give classical

parametric spectrum examples. We handle wave sta-

tistics in section 4. We discuss our results in section 5,

and conclude in section 6.

2 OCEAN MODELS

2.1 Deﬁnitions and Relationships

The surface elevation, η, is the vertical displacement

from the mean water level of the oceanic surface at

given point and time. The wave amplitude, a, is the

maximum surface elevation due to this wave. The

wave height, H, is the vertical distance between a

trough and an adjacent crest. For a single wave,

Fréchot J. (2006).

REALISTIC SIMULATION OF OCEAN SURFACE USING WAVE SPECTRA.

In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 76-83

DOI: 10.5220/0001357800760083

 SciTePress

H =2a. The wavelength, λ, is the distance between

two successive crests. The period, T , is the time inter-

val between the passage of successive crests through

a ﬁxed point. The frequency, f =1/T , is the number

of crests that pass a ﬁxed point in 1 second. The wave

speed or phase speed, c = λ/T , is the speed of wave

crests or troughs. It can also be expressed as c = ω/κ,

where ω =2πf is the angular velocity or angular fre-

quency, and κ =2π/λ is the wavenumber. The water

depth, d, is the vertical distance between the ﬂoor and

the mean water level.

The concept of deep water is wave dependent and

is related to the ratio of the water depth to the wave-

length of the wave. This comes from the transcenden-

tal expression

λ =

2π

tanh



2πd



, (1)

where g ≈ 9.807 m·s

−2

is the standard acceleration

of gravity. Since tanh(x) ≈ 1 when x>π, and

tanh(x) ≈ x when x<π/10, water is considered

deep if d/λ > 1/2 and shallow if d/λ > 1/20. This

leads to some simpliﬁcations in the expressions of the

terms given above (see table 1).

Table 1: Relations between oceanographic terms. The sub-

script ∞ indicates a deep water term.

Transitional depth: Deep water:

1/20 <d/λ<1/2

d/λ > 1/2

c =

2π

tanh(κd) c

∞

2π

tanh(κd) c

∞

)

κ =

2π

∞

= κ tanh(κd)

λ =

2π

= cT

λ =

2π

tanh(

2πd

) λ

∞

2π

λ = λ

∞

tanh(κd)

ω =

2π

= κc

= gκ tanh(κd)=gκ

∞

= gκ

2.2 Parametric Equations

The base model for ocean waves simulation comes

from the linear (or small-amplitude) wave theory by

(Airy, 1845), widely used in oceanic engineering, and

in Computer Graphics by (Peachey, 1986). It de-

scribes waves with a sinusoidal shape, which corre-

sponds to calm weather conditions. Considering a lo-

cation x

lying on a 1D surface at rest, the elevation

z = η at time t due to a wave with wavenumber κ,

amplitude a and angular velocity ω =

√

gκ is

z(x

,t)=a cos(κx

− ωt). (2)

When the steepness of the wave increases, its crests

become sharper and its troughs ﬂatter. Therefore,

(Fournier and Reeves, 1986) used a more realistic de-

scription based on trochoids, made by (von Gerstner,

1804) and by (Rankine, 1863). The surface equation

is now



x(x

,t)=x

+ a sin(κx

− ωt)

z(x

,t)=z

− a cos(κx

− ωt),

(3)

where z

is the surface elevation at rest (typically 0).

Note that the important point here is the phase term

difference of −π/2 between x(x

,t) and z(x

,t), not

the use of a particular sine or cosine function. This

Lagrangian model describes the trajectory in a ver-

tical plane of a particle (x, z) around its position at

rest (x

). Summing several waves and extending

equation 3 to a 2D surface gives

⎧

⎪

⎨

⎪

⎩

x(x

,t)=

x



κ

κa(κ)sin(κ · x

− ω(κ)t + φ(κ))

z(x

,t)=

−



κ

a(κ)cos(κ · x

− ω(κ)t + φ(κ)),

(4)

where x =(x, y) is the horizontal particle position at

time t, x

=(x

) its position at rest, κ =(κ

,κ

)

a wave vector, i.e. a vector with magnitude κ =

κ and direction of the considered wave propagation

and

κ = κ/κ is the unit vector of κ. Because of

the presence of uniformly distributed random phase

terms, φ(κ) ∈ [0, 2π[, this model is also known as

random waves. Any set of x

can be taken, which

allows the use of adaptive mesh, for optimal surface

sampling (Hinsinger et al., 2002).

2.3 Inverse Fourier Transform

Another method for computing equation 4 is the 2D

inverse discrete Fourier transform, used by (Mastin

et al., 1987), (Premo

ze and Ashikhmin, 2001) and

(Tessendorf, 2001). The set of N ×M complex num-

bers F

n,m

is transformed into a set of complex num-

bers f

p,q



n=1



m=1

n,m

exp



i2π





, (5)

where p ∈{1, .., N} and q ∈{1, .., M }. This is

of particular interest because the fast Fourier trans-

form (FFT) algorithm is an efﬁcient way to compute

REALISTIC SIMULATION OF OCEAN SURFACE USING WAVE SPECTRA

these sum. However, in comparison with the previous

method, its usage is more restrictive. The set of x

deﬁned as a regular grid of N ×M points with dimen-

sions L

×L

and origin at the center, such that x

/N, m

/M ), where n

∈ [−N/2,N/2[

and m

∈ [−M/2,M/2[ are integers. We rewrite

equation 4 as

⎧

⎪

⎨

⎪

⎩

x(x

,t)=x

+ 





κ

κA(κ, t)exp(iκ · x

)



z(x

,t)=z

−





κ

A(κ, t)exp(iκ · x

)



(6)

where () and () correspond, respectively, to the

imaginary part and real part of the expression, and

A(κ, t)=a(κ)exp(i(−ω(κ)t + φ(κ))). (7)

Rather than the random phase term φ, authors com-

monly use a normally distributed random amplitude

(see section 4). To comply with equation 5, the set of

wave vectors must be

κ =(2π

, 2π

), (8)

where n

and m

are deﬁned as n

and m

above.

The resulting surface is periodic in all directions and

can be used as a tile (Tessendorf, 2001).

To decrease the FFT computation time by a fac-

tor two, real numbers can be used instead of com-

plex ones. This is achieved by adding two waves with

same amplitude and travelling in opposite directions

(Tessendorf, 2001). Equation 7 becomes

A(κ, t)=a(κ)exp(i(−ω(κ)t + φ(κ)))

+ a(κ)exp(−i(−ω(κ)t + φ(κ)))

=2a(κ)cos(−ω(κ)t + φ(κ)).

(9)

This results in a single stationary wave with time de-

pendent amplitude. This phenomenon is known as

standing wave. The drawback of this method is that

the generated surface is only half the size of the ex-

pected one. The second half is obtained with a rota-

tion of the ﬁrst one by 180 degrees around the origin,

leading to pattern duplications.

3 WAVE SPECTRA

To be able to use the models discussed so far, we

need a function a(κ). For the parametric model, we

also need to know which set of wave vectors char-

acterizes the surface we want to generate. The more

natural method is to use records of surface elevation

measurement data used by oceanic engineering (Thon

and Ghazanfarpour, 2002). Measurements are made

with accelerometers mounted on buoys, satellite al-

timeters, high frequency radars and others techniques.

A spectral analysis of the collected data is done using

the Fourier transform from time domain to frequency

domain. This decomposition of the surface elevation

gives a histogram of wave frequencies ω, with corre-

sponding amplitudes and possibly directions, known

as frequency amplitude spectrum. The same analysis

method can be used with oceanic surface photographs

(Tessendorf, 2001) (Thon and Ghazanfarpour, 2002).

An amplitude spectrum can be used to generate a

surface with the same characteristics as the related

one. However, to get several oceanic surfaces with

different sea states, as many spectra are needed. In-

stead, we rely on parametric wave spectra, which can

ﬁt any environment conditions, like wind speed and

fetch.

3.1 Wave Energy and Amplitudes

Oceanographers are mostly concerned by wave en-

ergy rather than amplitude. For this purpose, they

use another type of spectrum, S(ω), called wave fre-

quency energy spectrum or wave spectrum, which

gives information about wave energy distribution as a

continuous function of frequency. This is a smoothed

version of a modiﬁed amplitude spectrum (see be-

low). Directional informations are taken into account

with a directional wave spectrum:

E(ω, θ)=S(ω)D(ω,θ), (10)

where θ is the direction of the wave and D(ω,θ) is a

directional spreading function, deﬁned such that



+π

−π

E(ω, θ)dθ = S(ω) (11)

for all values of ω. The Pierson-Moskowitz paramet-

ric wave spectrum (see section 3.2) has been regularly

used in the ﬁeld of Computer Graphics since (Mastin

et al., 1987) as a direct evaluation of wave amplitudes.

But this method cannot reﬂect statistical characteris-

tics of the oceanic surface. First, this is a continuous

function, so it needs to be integrated to be used with a

discrete model. Second, wave spectrum does not give

direct information about wave amplitude but energy.

The mean energy per unit surface area is E =

ρg var(η), where ρ is the water density and var(η) the

variance of the surface elevation. The wave spectrum

is deﬁned to be related to the surface energy by

var(η)=



+∞

S(ω)dω. (12)

For a zero mean process, like the sinusoidal wave

model from equation 2, the variance is

var(x)=x

rms

, (13)

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

where x

rms

is the root mean square of the values. For

a general process, this becomes x

rms

−¯x

. The mean

amplitude of the trochoidal wave model from equa-

tion 3 is ¯a = −(κa

)/2, which can be reasonably ne-

glected in most cases for practical purposes. So, we

apply equation 13 to this model as well for simplic-

ity. The rms of a sinusoidal or trochoidal wave with

amplitude a is

rms

. (14)

As we see the oceanic surface as the sum of many

waves with independent random phases, the total vari-

ance of the surface elevation is the sum of the variance

of each wave. So, taking a ﬁnite range of frequen-

cies [ω

min

,ω

max

] such that it is representative of the

whole energy, i.e.



max

min

S(ω)dω ≈



+∞

S(ω)dω, (15)

we divide it in N samples of width ∆ω

and tag the

mean frequency of each of them as ω

to get the rela-

tion

var(η)=



n=1

var(a(ω

)) =



n=1

a(ω

)

. (16)

Regarding equations 12 and 15, this is rewritten as

var(η)=



max

min

S(ω)dω =



n=1



∆ω

S(ω)dω,

(17)

and so we found the amplitude of each wave with

a(ω

)



∆ω

S(ω)dω ≈ 2 S(ω

)∆ω

. (18)

To take into account the direction of the wave, we

sample the whole directional spectrum E(ω, θ):

a(ω

,θ

)



∆ω



∆θ

E(ω, θ)dθ dω. (19)

So, for each wave with angular frequency ω and direc-

tion θ, we can now compute the corresponding ampli-

tude a(ω, θ).

3.2 Parametric Spectra

Parametric spectrum models are empirical expres-

sions with user deﬁned parameters that have been

found to ﬁt ocean surface elevation measurements.

Most common parameters include wind speed and di-

rection and fetch. They are useful to simulate realistic

ocean waves without measurement data, but can also

be altered to ﬁt speciﬁc data.

The base of modern parametric wave spectrum was

found by (Phillips, 1957) and has the form

(ω)=

αg

, (20)

where α =0.0081 is called the Phillips constant.

Taking into account wind speed, (Pierson and Mos-

kowitz, 1964) found an expression that describes a

theoretical fully developed sea with inﬁnite fetch (see

ﬁgure 1). The wind has blown with no change over

a large area for several hours, and waves growth is

almost null. The spectrum is

(ω)=S

(ω)exp



−







, (21)

where ω

is the frequency of the peak of the spectrum,

i.e. dS

/dω =0for ω

. Usual value for ω

0.855g

where U

is the wind speed at a height of 10 meters

above the sea surface.

0 0.2 0.4 0.6 0.8 1 1.2

variance (m

·s)

frequency (rad·s

−1

)

10.0 m·s

−1

12.5 m·s

−1

15.0 m·s

−1

17.5 m·s

−1

20.0 m·s

−1

Figure 1: Pierson-Moskowitz frequency spectrum S

(ω)

with different wind speed values U

For a fetch limited sea, where waves continue to

grow, the JONSWAP spectrum has been found by

(Hasselmann and al., 1973) to be more appropriate

(ﬁgure 2). This is the previous spectrum with an ad-

ditional term:

(ω)=S

(ω)γ

, (22)

with

r =exp



−

(ω − ω

)

2σ



Here, γ is a peak enhancement factor, i.e. when same

values are used for α and ω

in both spectra, we get

γ = S

(ω

)/S

(ω

). The parameter σ controls

the width of the peak. Usual parameter values for this

spectrum are

α =0.076





0.22

where F is the fetch in meters,

=22





1/3

REALISTIC SIMULATION OF OCEAN SURFACE USING WAVE SPECTRA

γ =3.3, but can vary between 1 and 7, and

σ =



0.07 if ω ≤ ω

0.09 if ω>ω

As the fetch is an important element of the sea state

description, we use the JONSWAP spectrum, rather

than the Pierson-Moskowitz one.

0 0.2 0.4 0.6 0.8 1 1.2

variance (m

·s)

frequency (rad·s

−1

)

Pierson-Moskowitz

100 km

200 km

300 km

400 km

Figure 2: JONSWAP frequency spectrum, S

(ω), with a

wind speed of U

=15m·s

−1

, and different fetch values F .

Other parametric spectrum models can be found

in oceanographic literature, including double peaked

spectrum for swell coming from distant storm. These

spectra are often expressed as a function of frequency

f = ω/(2π). To preserve integral equality, conver-

sion between spectra is done using substitution:



(f)df =



(ω)dω =



(ω(f))

dω



(2πf)2π df.

(23)

For the dispersion relation, we use the expression

found by (Longuet-Higgins, 1962):

D(ω,θ)=N(s(ω)) cos



− θ



2s(ω)

, (24)

where θ

is the main direction of the spectrum, usu-

ally the direction of the wind, and N (s(ω)) is a nor-

malization factor deﬁned as

N(s(ω)) =

√

Γ(s(ω)+1)

Γ(s(ω)+1/2)

and Γ() is the gamma function (ﬁgure 3). The func-

tion s(ω) controls the sharpness of the directional

spreading and has been deﬁned by (Mitsuyasu and al.,

1975) as

s(ω)=11.5





2.5





with

µ =



5 if ω ≤ ω

−2.5 if ω>ω

0.1 m

·s

1.1 m

·s

2.1 m

·s

π/2

−π/2

−π

direction (rad)

0.4

0.6

0.8

1.2

freq. (rad·s

−1

)

variance (m

·s)

Figure 3: 3D plot of the JONSWAP spectrum, E

(ω, θ),

with U

=25m·s

−1

, F = 100 km and θ

= 0 rad.

For a simple use, only wind speed, direction and

fetch need to be given to the spectrum. In order

to make the spectrum curve ﬁt particular data, like

oceanic measurements, the default parameter values

can be changed, until the desired curve shape is

reached (ﬁgure 4).

0.2

0.4

0.6

0.8

0.6 0.8 1 1.2 1.4 1.6 1.8

variance (m

·s)

frequency (rad·s

−1

)

α × 1.3

× 1.2

σ =0.03

γ =1

Figure 4: JONSWAP frequency spectrum, S

(ω), showing

how different parameter values alter the curve shape (U

15 m·s

−1

, F = 50 km).

3.3 Spectrum Sampling

We now look for a selection of wave frequencies and

directions. For the FFT based model, the size and

sample number of the rendered surface determine the

set of wave vectors to be used (see equation 8). For

the parametric one, as there is not such restriction,

we select waves that are the most representative of

the spectrum energy dispersion. For this purpose,

we sample the wave spectrum over a limited domain

[ω

min

,ω

max

] × [θ

min

,θ

max

]. We want this domain

to be the most representative of the whole spectrum,

i.e. we want it to be as dense as possible. So, by

iteration, we found one of the smallest domain that

contains roughly 95% of the total energy.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

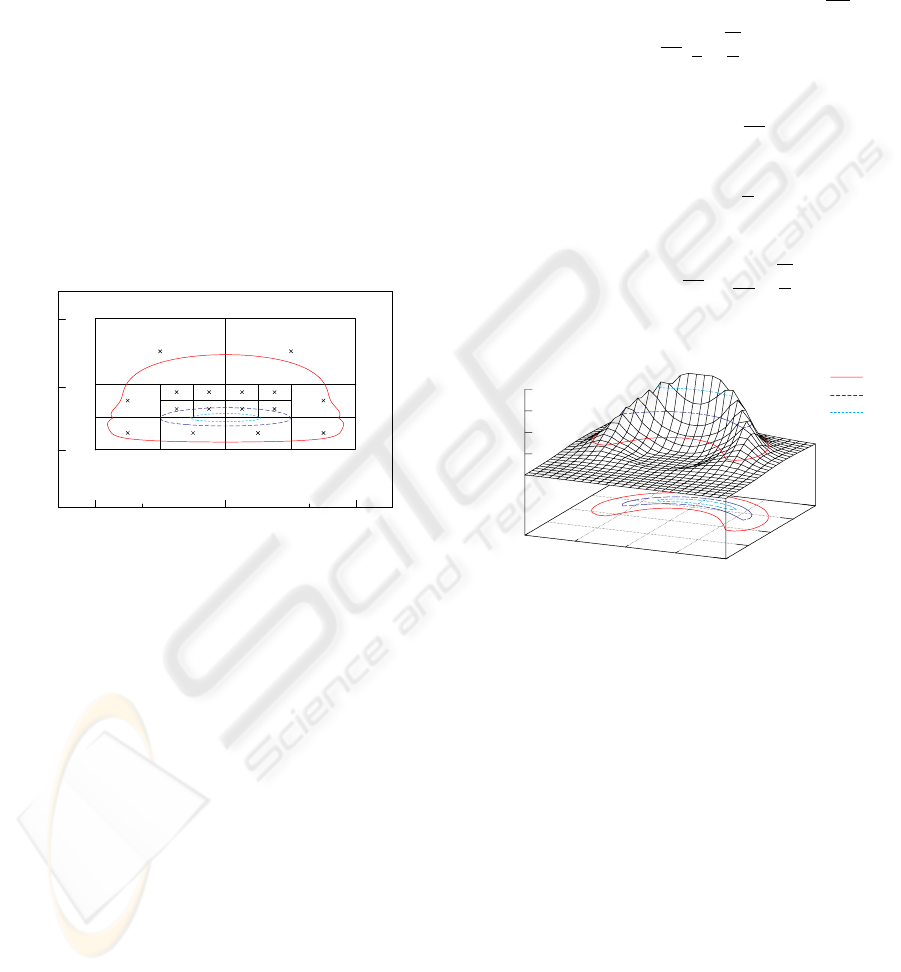
For simplicity, a regular sampling could be used

by taking a constant size ∆ω × ∆θ for each sam-

ple, with ∆ω =(ω

max

− ω

min

)/N and ∆θ =

(θ

max

− θ

min

)/M , where N and M are the num-

ber of frequency and angle samples, respectively. But

an adaptive sampling is more appropriate, especially

when few waves are summed, as this better reﬂects the

spectrum attributes. For this purpose, we over-sample

parts of the spectrum representing large amount of

energy, like (Thon and Ghazanfarpour, 2002). For a

given spectrum, we build a quadtree of 4+6n sam-

ples, where n is an integer. Samples have different

sizes but each of them roughly corresponds to the

same energy, and so the same amplitude. Sample cen-

ters give us corresponding wave vector polar coordi-

nates (ﬁgure 5). So, we now have a set of wave ampli-

tudes, frequencies and directions (a, ω, θ). In order to

use them with ocean models, we convert frequencies

to wavenumbers and polar coordinates to Cartesian

ones, to get a set of wave vectors (κ).

max

min

max

0θ

min

frequnecy (rad·s

−1

)

direction (rad)

Figure 5: 2D projection of the spectrum from ﬁgure 3,

showing adaptive sampling with 16 waves.

Using this method, we make oceanic surfaces with

realistic wave shapes and global structure which cor-

responds to the wanted weather condition. However,

if a close look at the surface is needed, we have to pay

special attention to short waves. When wind speed

or fetch increase, energy is transferred to lower fre-

quency waves, i.e. to high wavelength waves (see ﬁg-

ures 1 and 2). As we use adaptive sampling, we take

more samples for low frequencies and less for high

ones, resulting in a smoother surface at a human scale

and a lack of realism. So, the spectrum needs to be

sampled over a second domain corresponding to short

waves, up to the capillary wave size. This domain

must be close to the ﬁrst one, to avoid a “hole” in the

whole frequency range. The number of samples we

take can vary, depending of the distance between the

observer and the surface, in the spirit of (Hinsinger

et al., 2002).

For the FFT based model, we sample a spectrum

E(κ) in the Cartesian wavenumber domain (ﬁgure 6).

As the parametric spectra do not give same values

for a wave and its opposite (i.e. E(κ) = E(−κ)),

the real number method (equation 9) cannot be used.

To preserve integral equality, spectrum conversion is

done according to substitution rule. First, we convert

the frequency spectrum S

(ω) to a wavenumber spec-

trum S

(κ):



(κ)dκ =



(ω)dω =



(ω(κ))

dω

dκ



(

√

gκ)



dκ.

(25)

Second, we convert the wavenumber directional spec-

trum E

κ,θ

(κ, θ)=S

(κ)D(ω =

√

gκ, θ) from polar

coordinates to Cartesian ones:



κ

(κ)dκ =



κ,θ

(κ, θ)

dθ dκ. (26)

Finally, we get

κ

(κ)=E

ω,θ

(

√

gκ, θ)

2κ



. (27)

50 m

150 m

250 m

-4

-8

(10

−3

−1

)

-4

-8

(10

−3

−1

)

100

200

300

400

variance (m

)

Figure 6: The same spectrum as in ﬁgure 3, but in the wave

vector domain κ

× κ

(i.e. E

(κ)).

As the wavenumber vectors are set by the rendered

surface attributes, we cannot use adaptive sampling.

Furthermore, many vectors correspond to a negligible

energy amount but are still used. This is somehow

balanced by the effectiveness of the FFT algorithm:

for the same computation time, we can use a lot more

waves, and so spectrum samples, than with the para-

metric method. However, we have to deal with sur-

face size and sampling on one hand, and with spec-

trum sampling on the other hand. Looking at equa-

tion 8, we see that absolute values of wave vector

components κ

and κ

are bounded, i.e. 2π/L

≤

|κ

| <πN/L

and 2π/L

≤|κ

| <πM/L

. So,

we ﬁrst have to consider surface size L

× L

,as

it determines the lowest wavenumber value. Then,

we choose the number of surface (and so spectrum)

samples, knowing that it is related to the highest

wavenumber value.

REALISTIC SIMULATION OF OCEAN SURFACE USING WAVE SPECTRA

4 STATISTICAL PROPERTIES OF

THE OCEAN SURFACE

Measurements of oceanic wave statistics have shown

that, to a reasonable accuracy, the surface elevation η

follows a normal distribution. Attributes of oceanic

waves we simulate are consistent with these observa-

tions. If we look at the oceanic surface as an inﬁnite

sum of waves with inﬁnitely small amplitude, we see

that the wave spectrum is a probability density func-

tion of wave frequencies and directions. Furthermore,

the variance of the surface elevation is ﬁnite (equa-

tion 12). So, by virtue of the central limit theorem,

we know that the more waves we sum, the closer to

the normal distribution is the simulated surface eleva-

tion.

Another observed characteristic of oceanic waves

is that their heights follow a Rayleigh distribution,as

noted by (Fournier and Reeves, 1986). This distribu-

tion is used with a parameter σ = H

/2, where H

≈



var(η) is known as the signiﬁcant height. From

this, it can be shown that the probability that a wave

has a larger height than H

is exp(−2) ≈ 0.1353.

Since they use deﬁned amplitudes, the ocean mod-

els presented in section 2 are known as determinis-

tic methods. (Tucker et al., 1984) showed that uni-

formly distributed random phase terms φ should be

replaced with random amplitudes. An expression like

a cos(κx

− ωt + φ) becomes

a cos(κx

− ωt)+r

a sin(κx

− ωt)

= Ra sin(κx

− ωt +Φ),

(28)

where r

and r

are random numbers from the stan-

dard normal distribution, i.e. with a mean of zero and

a standard deviation of one, R =



+ r

follows a

Rayleigh distribution and

Φ=

⎧

⎪

⎨

⎪

⎩

arctan





if r

≥ 0

arctan





+ π if r

< 0.

This non-deterministic method has better statistical

properties than the previous one. In order to use it

with parametric and FFT methods, we rewrite equa-

tions 4 and 6 according to equation 28.

5 RESULTS AND DISCUSSION

We made a simple real-time implementation of ocean

models. We focused on wave shapes and animations,

without considering effects like Fresnel reﬂectivity

and transmissivity, or foam and spray (ﬁgure 7). Of

course, rendering could have been achieved with clas-

sical high quality techniques as well. Interactions of

objects with ocean surfaces are not specially handled

by the Lagrangian model we use, and are beyond the

scope of this paper.

Since our method preserves the main spectrum en-

ergy, the global structure of the rendered surface is in-

dependent of the number of waves we sum. For both

ocean models, the sea state we get is always consis-

tent with the provided wind parameters, which cannot

be achieved with other existing methods. Since these

parameters are the only ones needed to have full con-

trol of the method, there is no need for the user to

adjust the resulting surface by trial and error.

As previously noted, the FFT model can be partic-

ularly tedious to use. To catch a reasonable part of the

spectrum, the grid length and the number of samples

have to be carefully chosen, whatever are the desired

surface characteristics. For example, taking 512 sam-

ples up to a frequency of 25 rad·s

−1

requires a grid

length of no more than 25 m. Furthermore, as this

leads to a lowest frequency of about 1.5 rad·s

−1

, the

spectrum peak may be under-sample.

We have tested our implementation with a 3 GHz

Pentium 4 PC and a Radeon 9200 graphic board. With

the FFT model, we got about 65 fps and 13 fps with,

respectively, a grid of 128 × 128 and 256 × 256 sam-

ples. With the parametric equations, we got 8 fps with

a regular grid of 128 × 128 samples and 50 waves.

And taking less than 100 waves leads to poor detailed

results. Clearly, only the FFT can reach interactive

rate. Although we do not implement an adaptive sur-

face mesh, it seems obvious this could not compete

with the FFT speed. Parametric equations should be

kept for non-interactive rendering, since they are eas-

iest to use.

6 CONCLUSION

We have presented a method for accurate wave energy

spectrum sampling that allows realistic ocean surface

synthesis and animation. For given wind parameters,

the wave heights and directions are computed such

that statistical properties of the resulting surface are

correct. Since it does not rely on any ocean model,

this method is suitable for Gerstner equations and

Fourier transforms.

ACKNOWLEDGMENTS

The author wish to thank Bertrand le Sa

ec and Jean-

Christophe Gonzato for rereading this paper.

GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS

Figure 7: FFT with a grid of 512 × 512 samples. Left: grid length is 50 m and wind speed is 5 m·s

−1

. Middle: grid length

is 450 m and wind speed is 15 m·s

−1

. Right: grid length is 1500 m and wind speed is 25 m·s

−1

. White square is 1 m wide.

REFERENCES

Airy, G. B. (1845). Tides and waves. In Encyclopaedia Me-

tropolitana, volume 5, chapter 192, pages 241–396.

Cieutat, J.-M., Gonzato, J.-C., and Guitton, P. (2001). A

new efﬁcient wave model for maritime training simu-

lator. In Spring Conference on Computer Graphics.

Enright, D., Marschner, S., and Fedkiw, R. (2002). Anima-

tion and rendering of complex water surfaces. In Conf.

on C. G. and interactive techniques, pages 736–744.

Fournier, A. and Reeves, W. T. (1986). A simple model

of ocean waves. SIGGRAPH Computer Graphics,

20(4):75–84.

Gamito, M. N. and Musgrave, F. K. (2002). An accurate

model of wave refraction over shallow water. Com-

puters & Graphics, 26(2):291–307.

Gonzato, J.-C. and le Sa

ec, B. (2000). On modeling and

rendering ocean scenes. Journal of visualisation and

computer simulation, 11:27–37.

Hasselmann, K. and al. (1973). Measurements of wind-

wave growth and swell decay. Erg

anzungsheft zur

Deutschen Hydrographischen Zeitschrift, (12).

Hinsinger, D., Neyret, F., and Cani, M.-P. (2002). Inter-

active animation of ocean waves. In Symposium on

Computer Animation, pages 161–166.

Iglesias, A. (2004). Computer graphics for water modeling

and rendering: a survey. Future generation computer

systems, 20(8):1355–1374.

Longuet-Higgins, M. S. (1962). The distribution of inter-

vals between zeros of a stationary random function.

Philosophical Transactions for the Royal Society of

London, 254:557–599.

Mastin, G. A., Watterberg, P. A., and Mareda, J. F. (1987).

Fourier synthesis of ocean scenes. IEEE Computer

Graphics and Applications, 7(3):16 – 23.

Mihalef, V., Metaxas, D., and Sussman, M. (2004). Anima-

tion and control of breaking waves. In Symposium on

Computer Animation, pages 315–324.

Mitsuyasu, H. and al. (1975). Observations of the direc-

tional spectrum of ocean waves using a cloverleaf

buoy. Jour. of physical oceanography, 5(4):750–760.

Peachey, D. R. (1986). Modeling waves and surf. SIG-

GRAPH Computer Graphics, 20(4):65–74.

Phillips, O. M. (1957). On the generation of waves by tur-

bulent wind. Journal of ﬂuid mechanics, 2:417–445.

Pierson, W. J. and Moskowitz, L. (1964). A proposed spec-

tral form for fully developed wind seas. Journal of

geophysical research, 69:5181–5203.

Premo

ze, S. and Ashikhmin, M. (2001). Rendering natural

waters. Computer Graphics Forum, 20(4):189–199.

Rankine, W. J. M. (1863). On the exact form of waves near

the surface of deep water. Philosophical transactions

of the Royal society of London, pages 127–138.

Tessendorf, J. (2001). Simulating ocean water. ACM SIG-

GRAPH course notes. Updated in 2004.

Thon, S. and Ghazanfarpour, D. (2002). Ocean waves syn-

thesis and animation using real world information.

Computers and Graphics, 26(1):99–108.

Tucker, M. J., Challenor, P. G., and Carter, D. J. T. (1984).

Numerical simulation of a random sea. Applied ocean

research, 6(2):118–122.

von Gerstner, F. J. (1804). Theorie der wellen. Abhand-

lungen der K

oniglichen B

ohmischen Gesellschaft der

Wissenschaften, 1:1–65.

REALISTIC SIMULATION OF OCEAN SURFACE USING WAVE SPECTRA