
DANCE EVALUATION SYSTEM BASED ON MOTION
ANALYSIS
Masahiro Tada, Masahide Naemura
ATR Media Information Science Laboratories, 2-2-2 Hikaridai, Keihanna Science City, Japan
Keywords: Motion Analysis, Wavelet Multi-Resolution Correlation Analysis, Edutainment System, Dance.
Abstract: We are conducting research on computer-aided edutainment with a view to creating learning environments
where anybody can acquire advanced skills. In this paper, we focus on dance actions as a part of
edutainment research and propose a method to evaluate dance skills through motion analysis. Our method
consists of wavelet multi-resolution analysis and correlation analysis. Firstly, by using wavelet multi-
resolution analysis, we decompose complex dance motion data acquired from a motion-capture system into
different frequency components. And by applying correlation analysis to the decomposed data, we extract
motion features that play a dominant role in evaluating sense of rhythm and harmony of movement of each
body part. By comparing the extracted features of amateurs to those of experts, we have achieved a
quantitative evaluation method for dance skills. Through experiments, we confirmed that there is a strong
correlation amongst extracted motion features and subjective evaluation results of dance skills. Using the
proposed method, we have developed a computer-aided edutainment system for dance. By mapping motion-
captured dance data and its evaluation results onto the 3-D CG figure, our system enables users to visually
know bad points of their dance and acquire more advanced dance skills.
1 INTRODUCTION
We are conducting research on computer-aided
edutainment with a view to creating learning
environments where anybody can acquire advanced
skills (Naemura, 2005, Oshima, 2004). In order to
make good use of computer technology in
edutainment, it is important to identify the basic
factors that characterize the performance difference
between an amateur and an expert and to
computationally analyse the difference. In this
paper, we focus on dance actions as a part of
edutainment research.
We can roughly classify dance into two
categories: formal dance and rhythmical dance.
Formal dance (e.g. ballet) has precise and highly
formalized set steps and gestures, whereas
rhythmical dance (e.g. jazz dance, hip-hop dance)
emphasizes improvisation.
There are many works that focus on formal
dance; e.g. classic ballet (Soga, 2001), traditional
folk dance (Shiratori, 2004, Hachimura, 2005). Most
aim to digitally archive the dance of experts as
intangible cultural heritage, and do not consider
amateur dance at all.
Compared to formal dance, there are few works
on rhythmical dance. However, in recent years,
popularity of rhythmical dance (especially hip-hop
dance) is rapidly increasing. Therefore, in this paper,
we focus on hip-hop dance.
As a dance analysis method, Laban Movement
Analysis (LMA, Bartenieff, 1980) is widely used
(Naugle, 1999, Camurri, 1999, Hachimura, 2005).
LMA is a methodology classifying dynamical and
geometrical features of body motions in detail.
Nevertheless, LMA does not deal with rhythm that is
an essential factor of hip-hop dance.
Our goal is to develop an evaluation method for
rhythmical dance and help amateurs acquire
advanced dance skills. In this paper, we propose an
evaluation method for rhythmical dance based on
wavelet multi-resolution analysis and motion
correlation analysis.
2 MOTION CAPTURE SYSTEM
A motion capture system is one of the most effective
methods for digitalizing human motions. Therefore,
in order to acquire dance action movements, we use
243
Tada M. and Naemura M. (2006).
DANCE EVALUATION SYSTEM BASED ON MOTION ANALYSIS.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 243-250
DOI: 10.5220/0001358602430250
Copyright
c
SciTePress
an optical motion capture system (Vicon612).
Vicon612 uses 12 infrared cameras to detect
reflective markers (small balls) attached to a dancer.
Spatial resolution of Vicon612 is about 2mm, and
sampling interval is set at 1/60 second. The number
of markers attached to a dancer is 30. Based on
acquired three-dimensional coordinate positions of
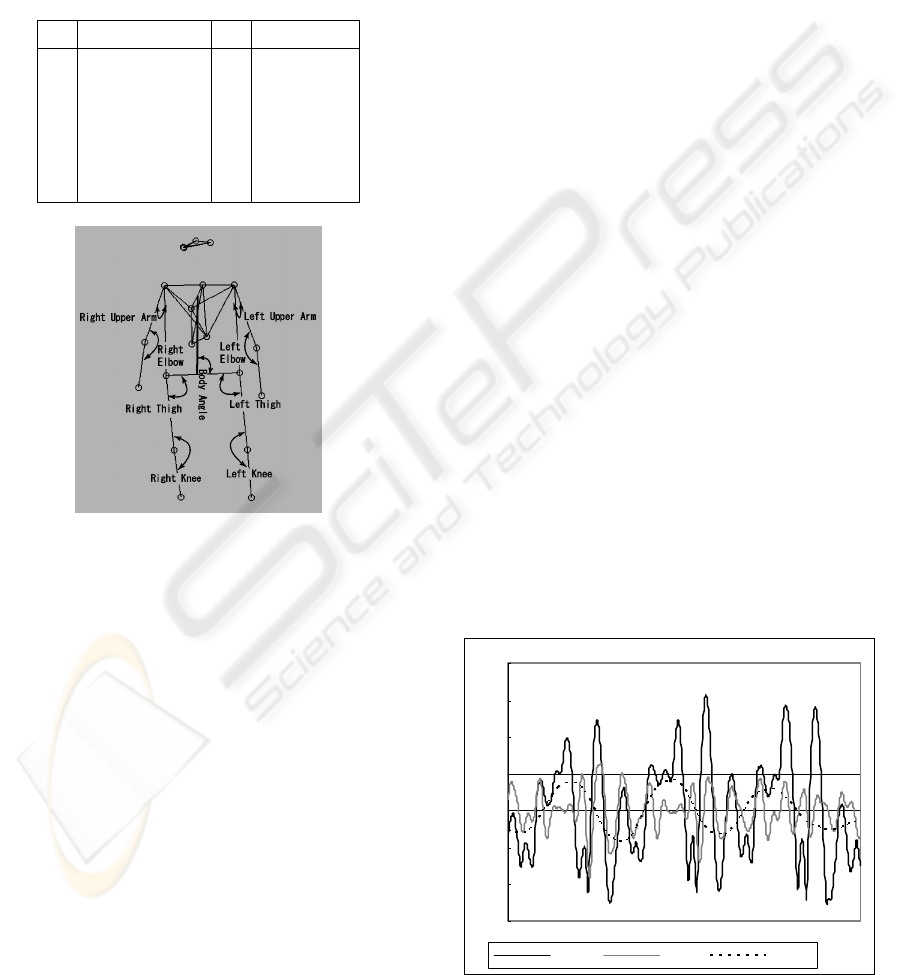
markers, we calculate joints angles shown in Table 1
and Fig.1.
Table 1: Adopted joints angles.
ID Joints ID Joints
0 Right Elbow 5 Left Knee
1 Left Elbow 6
Right
Thigh
2
Right Upper
Arm
7
Left
Thigh
3
Left Upper
Arm
8
Body
Angle
4 Right Knee
Figure 1: Adopted joints angles.
3 MULTI-RESOLUTION
ANALYSIS
In human motions, there are many correlations
among joint actions. Nakata (2005) proposed a
behaviour recognition method based on motion
correlation analysis. However, dance motion is very
complex. It is a mixture of various kinds of motions,
each having a different period. This complexity
would give a negative effect to motion correlation
analysis. Therefore, firstly, by using a multi-
resolution discrete wavelet transform (DWT), we
decompose complex dance motion data acquired
from a motion-capture system into different
frequency components.
3.1 Discrete Wavelet Transform
Multi-resolution DWT can provide information of
signals both in the time domain and in the frequency
domain. A wavelet transform can be obtained by
projecting the signal onto a scaled and translated
version of a basic function. This function is known
as mother wavelet, Ψ(t). A mother wavelet must
satisfy following conditions.
.1)(,0)(
2
∫∫
∞
∞−
∞
∞−
== dttdtt
ψψ
(1)
A scaled and translated mother wavelet Ψ
j,k
(t)
forms basis of functions. By discretizing scaling
parameters and translating parameters, Ψ
j,k
(t) is
represented as
.)2(2)(
2/
,
ktt
jj
kj
−=
−−
ψ
ψ
(2)
The variables j and k are integers that scale and
translate the mother wavelet Ψ(t) to generate
wavelets. The scaling index j indicates the wavelet’s
width, and the translating index k gives its position.
By using (2), wavelet coefficient d
j,k
is represented
as follows.
,)()(
,,
∫
∞
∞−
= dttxtd
kjkj
ψ
(3)
where x(t) is time-series joint-angle data. The
wavelet coefficient d
j,k
represents information at a
particular resolution (2
-j
) at a particular spatial
location (2
j
k) of x(t). Therefore, a frequency
component of x(t) corresponding to resolution 2
-j
can
be represented as follows.
.)()(
,,
∑
=
k
kjkjj
tdtx
ψ
(4)
x
j
(t) is called as level-j wavelet detail. High-level
wavelet details represent low frequency components.
Fig.2 shows time-series right-elbow angle data
acquired from motion capture system and its wavelet
details.
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
t
Original Level5 Level8
Figure 2: Right-elbow angle data of a dancer and its
wavelet details.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
244
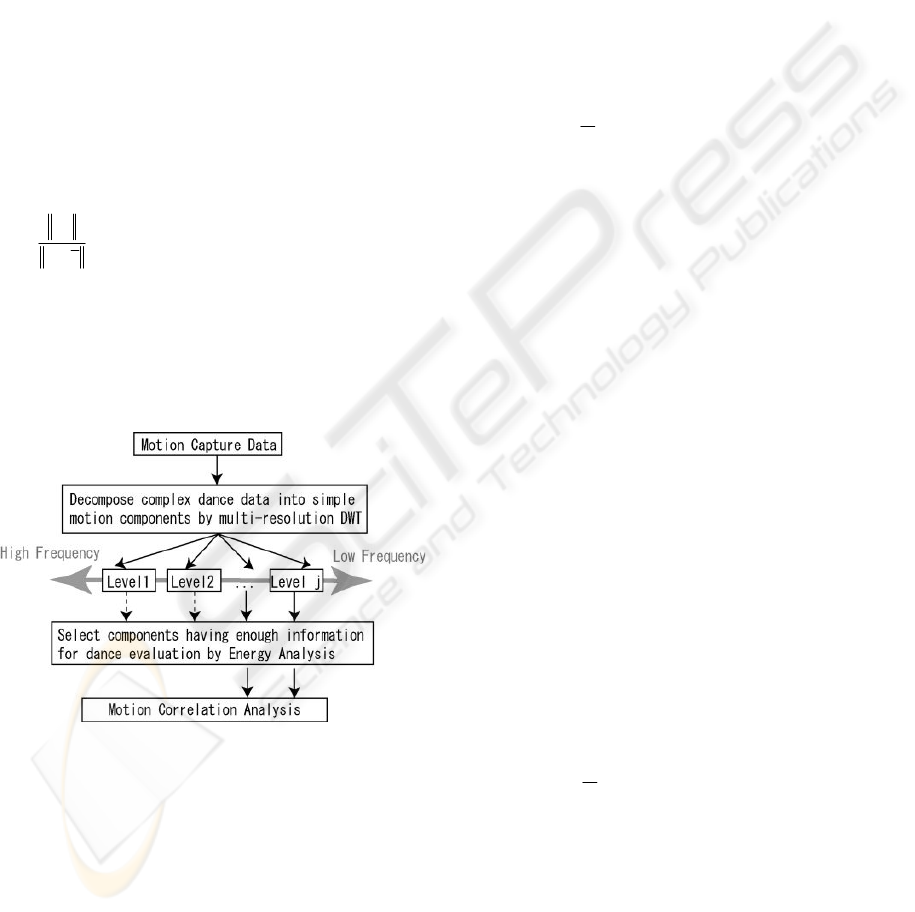
3.2 Energy Analysis
By using multi-resolution DWT, we can decompose
complex dance motion data into different frequency
components (wavelet details). However, not all the
components are important for evaluation of dance
skills; high frequency components (low-level
wavelet details) may contain only noise, whereas
low frequency components (high-level wavelet
details) may contain only too little and coarse
information.
Since a multi-resolution DWT conserves signal
energy (Walker, 1999), by comparing each
frequency component’s energy, we can select
components having enough information for
evaluation of dance skills.
Based on energy analysis, we define the
contribution ratio of the level-j wavelet detail as
,
x
c
j
j
−
=
x
d
(5)
where x is time-series angle data and d
j
is level-j
wavelet coefficient vector of x.
In this paper, wavelet details whose contribution
ratios exceed particular criteria are selected. Using
the selected wavelet details, we evaluate dance skills.
Figure 3: Overview of Multi-Resolution Analysis.
4 EVALUATION METHOD OF
DANCE SKILL
In order to evaluate dance skill, we employ (1) sense
of rhythm and (2) harmony of movement of all body
parts as evaluation criteria.
4.1 Evaluation Method of Sense of
Rhythm
Dancing to the rhythm of music is very important for
rhythmical dance. When a dancer moves his/her
limbs to the rhythm of music, each limb will draw a
periodic (proportion to beat-to-beat period)
trajectory.
In this paper, we propose an evaluation method of
sense of rhythm based on the autocorrelation
function and beat-to-beat interval information of
music.
Autocorrelation function of level-j wavelet detail
is defined as
,)()(
1
lim)(
2/
2/
0
,
∫
−
→
+=
T
T
jj
T
jxx
dttxtx
T
R
ττ
(6)
where x
j
(t) is level-j wavelet detail. R
xx,j
(τ) takes its
maximum at τ=0, and if x
j
(t) is periodic, R
xx,j
(τ)
attains its peak at τ=nT
j
, where T
j
is a period of x
j
(t)
and n is an integer.
Let us assume that beat-to-beat interval of music
is τ
b
, then autocorrelation function of motion data
moving perfectly to the rhythm of music will attain
its peak at τ=n τ
b
, where n is an integer. Therefore,
as a criterion for evaluating dancer’s sense of
rhythm, we employ the peak value of R
xx,j
(τ) and
difference between T
j
and τ
b
.
4.2 Evaluation Method of Harmony
of Movement of Each Body Part
Since dance is a gesture of the whole body, harmony
of movement of all body parts is essential. Therefore,
in this paper, we propose a method to evaluate
harmony of movement of each body part based on
the mutual-correlation function and beat-to-beat
interval information of music.
Let x
j
(t) and y
j
(t) be the level-j wavelet detail of
time-series angle data x(t), y(t) respectively. Then,
mutual-correlation function of x
j
(t) and y
j
(t) is
defined as follows.
.)()(
1
lim)(
2/
2/
0
,
∫
−
→
+=
T
T
jj
T
jxy
dttytx
T
R
ττ
(7)
If x
j
(t) and y
j
(t) are periodic, and move in
harmony with each other, R
xy,j
(τ) attains its peak at
τ=nT
j
, where T
j
is a period of x
j
(t), y
j
(t). Therefore,
as a criterion for evaluating harmony of movement
of body parts, we employ the peak value of R
xy,j
(τ)
and difference between T
j
and τ
b
.
Although there are many combinations of body
parts to calculate mutual-correlation functions, we
DANCE EVALUATION SYSTEM BASED ON MOTION ANALYSIS
245
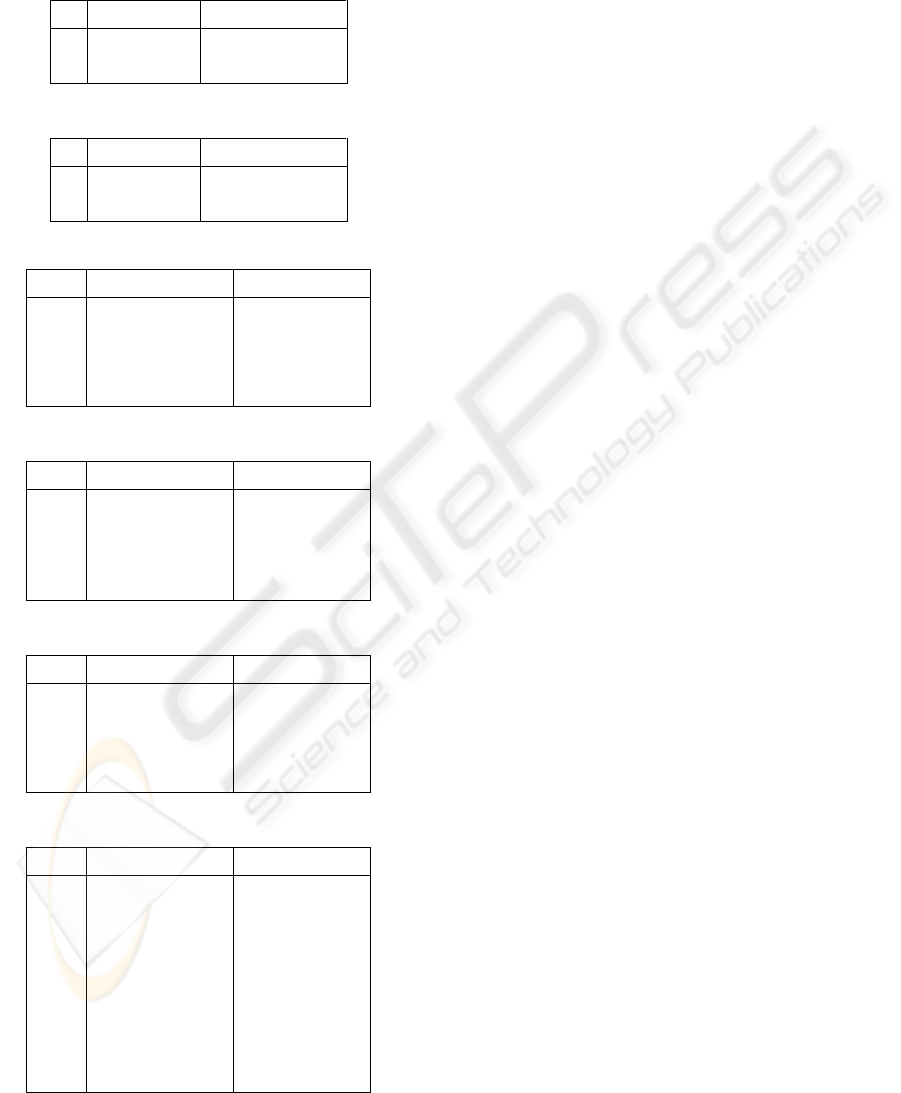
adopted 24 pairs of body parts shown in Table 2
under consideration of dance motion's characteristics.
Table 2: Pairs of Body Parts for Evaluation of Harmony of
Movements.
Harmony of Arm Parts
ID Body Part A Body Part B
0 Right Elbow Right Upper Arm
1 Left Elbow Left Upper Arm
Harmony of Leg Parts
ID Body Part A Body Part B
2 Right Knee Right Thigh
3 Left Knee Left Thigh
Harmony of top and bottom Parts
ID Body Part A Body Part B
4 Right Upper Arm Right Thigh
5 Left Upper Arm Left Thigh
6 Right Elbow Right Knee
7 Left Elbow Left Knee
Harmony of right and left Parts
ID Body Part A Body Part B
8 Right Upper Arm
Left Upper
Arm
9 Right Elbow Left Elbow
10 Right Thigh Left Thigh
11 Right Knee Left Knee
Harmony of Diagonal Parts
ID Body Part A Body Part B
12 Right Upper Arm Left Thigh
13 Left Upper Arm Right Thigh
14 Right Elbow Left Knee
15 Left Elbow Right Knee
Harmony of Body-Angle and Limbs
ID Body Part A Body Part B
16 Right Elbow
17 Left Elbow
18 Right Upper Arm
19 Left Upper Arm Body Angle
20 Right Thigh
21 Left Thigh
22 Right Knee
23 Left Knee
5 EXPERIMENTS
In our experiment, we let 4 dancers (1 expert and 3
amateurs) dance (7 kinds of hip-hop dance) to the
rhythm of music, and acquired their dance motions
using Vicon612.
Based on the acquired three-dimensional
coordinate positions of markers, we calculate joint
angles (Fig.1, Table 1), and decompose the data into
different frequency components (wavelet details)
using multi-resolution DWT. After selecting
important wavelet details by contribution ratios, we
evaluate each dancer’s skill.
5.1 Subjective Evaluation of Dance
Firstly, in order to confirm the subjective difference
in dance skill between an expert and an amateur, we
carried out a subjective evaluation experiment using
20 evaluators. We showed captured dances to
evaluators at random, and let them select the best
dance. As a result, all evaluators selected the
expert’s dance as the best one. This result shows that
there is a significant difference between the expert’s
dance and amateurs’ dance from the subjective
viewpoint. In the following sections, we try to
quantitatively evaluate this difference.
5.2 Evaluation Result of Sense of
Rhythm
Fig.4, 5 show the expert’s autocorrelation functions
(level-4, 6). X axis represents joints (numbers on x
axis correspond to ID in Table 1) and y axis is τ.
Colour of pixels in the figure represents the value of
autocorrelation functions. White pixels represent
strong positive correlation, black pixels represent
strong negative correlation, and gray pixels represent
week correlation. Dashed lines in the figure
represent beat-to-beat interval of the music.
Level-4 wavelet details capture short-period
motions (i.e. subtle motions), whereas level-6
wavelet details capture long-period motions (i.e.
general motions). As shown in Fig.4, 5, each
autocorrelation function peaks at the same time, and
the period of each joint’s motion is almost equal to
beat-to-beat interval of the music; i.e. the expert
moves her body parts completely to the rhythm of
music. These results show that the expert pays
conscious attention to subtle dance motions as well
as general dance motions.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
246
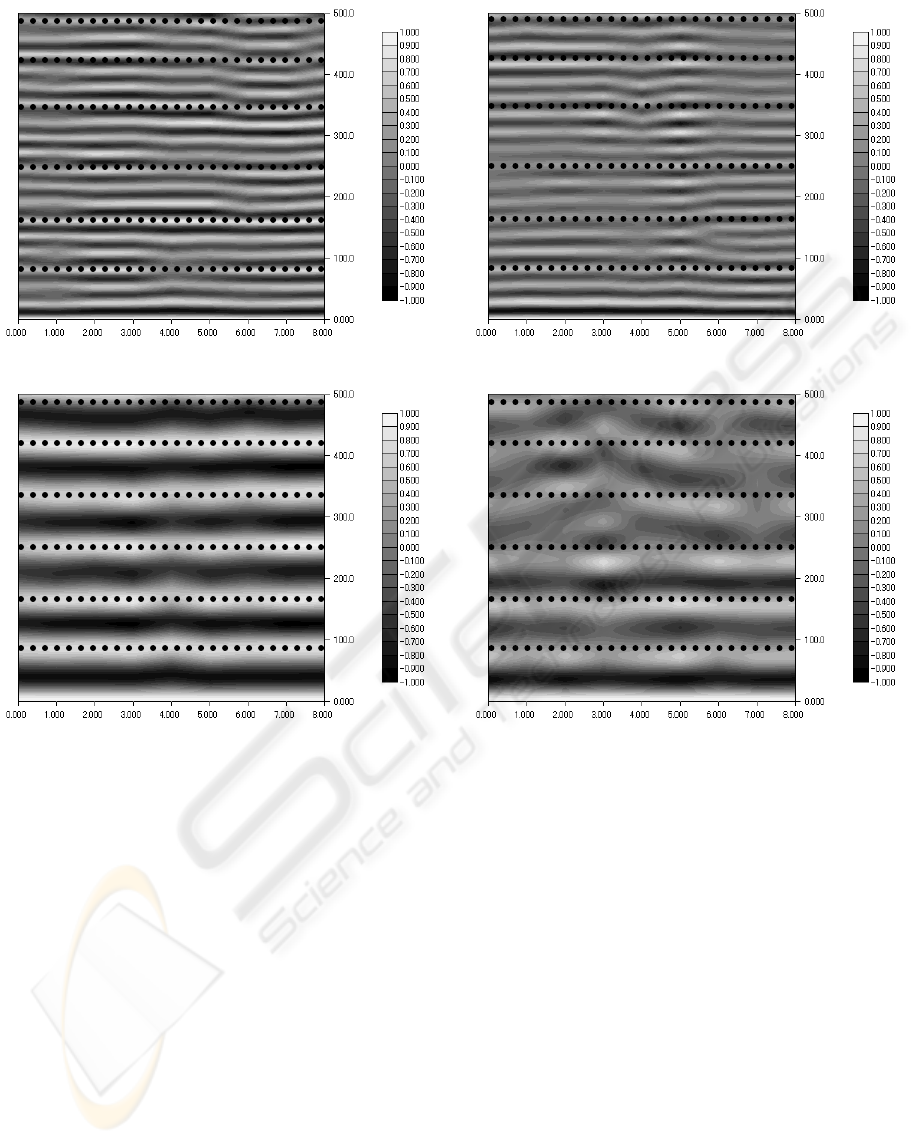
Figure 4: Expert’s autocorrelation functions (Level-4).
Figure 5: Expert’s autocorrelation functions (Level-6).
Fig.6, 7 show an amateur’s autocorrelation
function (level-4, 6). Most pixels in Fig.7 are gray;
i.e. most of level-6 wavelet details of amateur’s
dance motion data are not periodic. However, as
shown in Fig.6, when focusing on short-period
motions, most of autocorrelation functions attain
their peaks at the same timing that corresponds to
the beat-to-beat interval. These results show that
whereas the amateur can move her limbs at each
moment, she can't pay conscious attention to long-
period dance motions.
Figure 6: Amateur’s autocorrelation functions (Level-4).
Figure 7: Amateur’s autocorrelation functions (Level-6).
5.3 Evaluation Result of Harmony of
Movement of Each Body Parts
Fig.8, 9 show expert’s mutual-correlation functions
(level-4, 6). X axis represents pairs of body parts
(numbers on x axis correspond to ID in Table 2) and
y axis is τ.
As shown in Fig.8, 9, each mutual-correlation
function peaks (bottoms) at almost the same time; i.e.
in expert’s dance, each body part moves to make a
good harmony with the other body parts.
DANCE EVALUATION SYSTEM BASED ON MOTION ANALYSIS
247
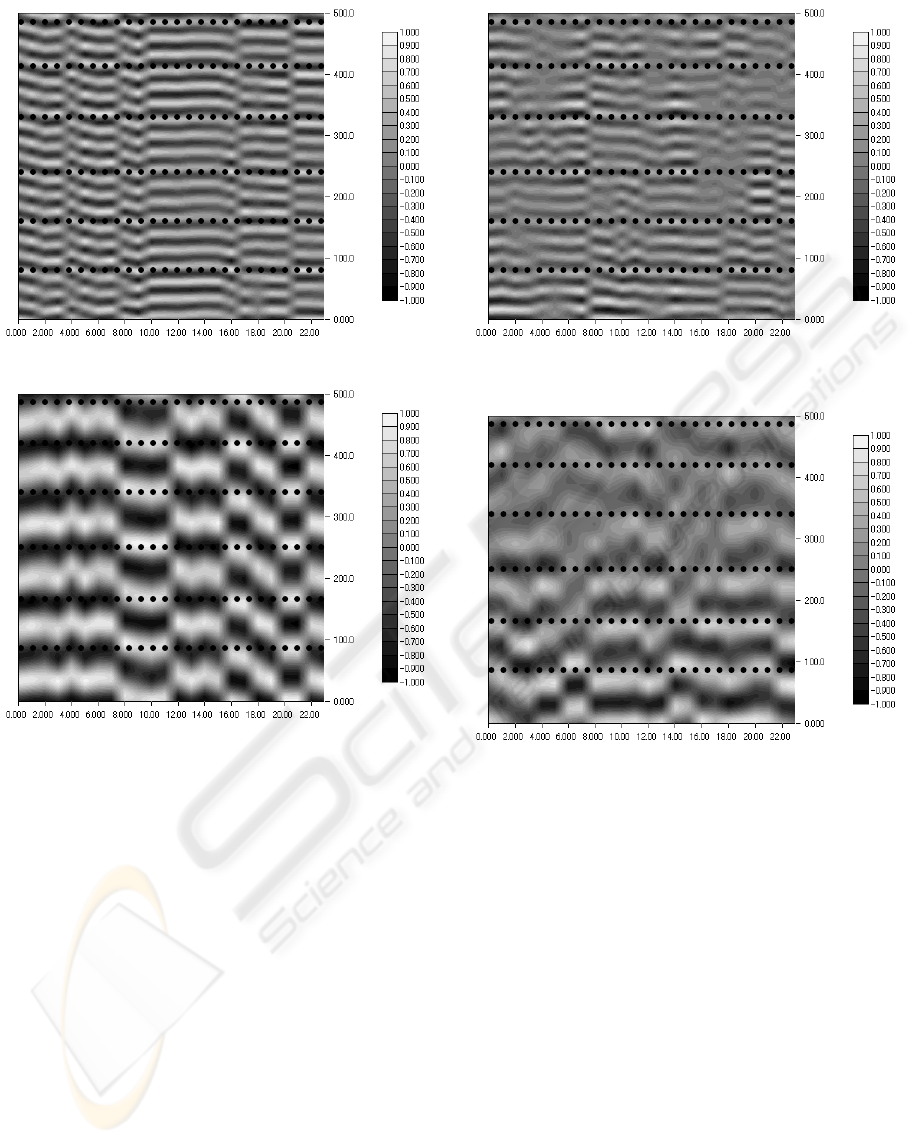
Figure 8: Expert’s mutual-correlation function (Level-4).
Figure 9: Expert’s mutual-correlation functions (Level-6).
Fig.10, 11 show the amateur’s mutual-correlation
functions (level-4, 6). Most pixels in Fig.10, 11 are
gray; i.e. in the amateur’s dance, most of body parts
move separately without considering harmony.
As shown above, the proposed evaluation
method shows that whereas the expert pays
conscious attention to subtle dance motions and to
the harmony of whole body parts, the amateur only
moves her limbs separately as an approximation of
dance.
Figure 10: Amateur’s mutual-correlation functions
(Level4).
Figure 11: Amateur’s mutual-correlation functions
(Level6).
5.4 Comparison: Evaluation Result
WITHOUT Multi-Resolution
DWT
To evaluate efficiency of multi-resolution DWT, we
also evaluate harmony of movement of all body
parts using “normal (without DWT)” mutual-
correlation functions as a comparison.
Fig.12 shows the expert’s mutual-correlation
functions (without DWT), and Fig.13 shows the
amateur’s. Whereas we can see clear difference
between Fig.8, 10 and Fig.9, 11, there is little
difference between Fig.12 and Fig.13. Most pixels in
Fig.12, 13 are gray; without multi-resolution DWT,
no strong motion correlation has appeared on dance
motion data.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
248

Figure 12: Expert’s mutual-correlation functions
WITHOUT DWT.
Figure 13: Amateur’s mutual-correlation functions
WITHOUT DWT.
These results show that complexity of dance
motion would give a negative effect to motion
correlation analysis. By decomposing complex
dance motions into simple motion components using
multi-resolution DWT, we can cancel the negative
effect to motion correlation analysis.
Fig.14 shows the expert’s mutual-correlation
function with DWT between left-thigh and body
angle, and Fig.15 shows the amateur’s. X axis
represents level of wavelet details, and y axis is τ.
As shown in Fig.14, by decomposing complex dance
motions into simple motions, strong correlations
have appeared on the expert's dance. In contrast, as
shown in Fig.15, no strong correlation has appeared
on the amateur's dance. These results show that
decomposition of complex dance motions by DWT
is indispensable to evaluate dance skills.
Figure 14: Expert’s mutual-correlation functions between
left-thigh and body angle with DWT (Level 4-6).
Figure 15: Amateur’s mutual-correlation functions
between left-thigh and body angle with DWT (Level 4-6).
6 DANCE EVALUATION SYSTEM
As discussed in Sec.5, by using the proposed method,
we can evaluate dance skills. However, it is difficult
to instinctively know bad points of a dance from
patterns like Fig.10. Therefore, in this paper, we
score an amateur’s dance skill by comparing
evaluation results of the amateur (e.g. Fig.10) to
those of the expert (e.g. Fig.8) by DP matching
(Cormen, 2001). By mapping motion-captured dance
data and its scoring result onto the 3-D CG figure,
we have developed a computer-aided edutainment
system for dance (Fig.16). Colour of balls attached
to each joint of 3D CG figure shows evaluation
result; blue balls represent a good score, and red
balls represent a bad score. By using our system,
amateurs are able to visually know the bad point of
DANCE EVALUATION SYSTEM BASED ON MOTION ANALYSIS
249

their dance, and to check their dance from any
viewpoint in a 3D CG space.
7 CONCLUSION
In this paper, we have developed an evaluation
method for rhythmical dance based on wavelet
multi-resolution analysis and motion correlation
analysis. A dance motion is a mixture of various
kinds of motions, each having a different period.
This complexity would give a negative effect to
motion correlation analysis. Therefore, by using
wavelet multi-resolution analysis, we decompose
complex dance motion data acquired from a motion-
capture system into different frequency components.
And by applying correlation analysis to the
decomposed data, we extract motion features that
play a dominant role in evaluating sense of rhythm
and harmony of movement of each body part. By
comparing the extracted features of amateurs to
those of experts, we have achieved a quantitative
evaluation method for dance skills.
Using the proposed method, we have developed a
computer-aided edutainment system for dance. By
mapping motion-captured dance data and its
evaluation results onto the 3-D CG figure, our
system enables users to visually know bad points of
their dance.
Figure 16: Screen shot of computer-aided edutainment
system for dance.
Figure 17: Expert’s Dance and Amateur’s Dance.
ACKNOWLEDGEMENTS
This research was partially supported by Japan
Society for the Promotion of Science, Grant-in-Aid
for Scientific Research (B), 1600038, 2004, and a
grant for “Research on Interaction Media for High-
Speed and Intelligent Networking” from the
National Institute of Information and
Communications Technology, Japan.
REFERENCES
Naemura, M. and Suzuki, M., 2005. Extraction of
Rhythmical Factors on Dance Actions through Motion
Analysis, In Proc. IEEE WACV2005.
Oshima, C., et al., 2004. Family Ensemble: A
Collaborative Musical Edutainment System for
Children and Inexperienced Parents, In Proc. ACM
MM2004.
Soga, A., et al., 2001. Motion Description and Composing
System for Classic Ballet Animation on the Web. In
Proc. 10
th
IEEE Roman.
Shiratori, T., et al., 2004. Detecting Dance Motion
Structure through Music Analysis, In Proc. 6
th
IEEE
International Conference on Automatic Face and
Gesture Recognition.
Hachimura, K., et al., 2005. Analysis and Evaluation of
Dancing Movement Based on LMA, In Proc. IEEE
International Workshop on Robots and Human
Interactive Communication.
Naugle, L. M., 1999. Motion Capture: Re-Collecting the
Dance, In Proc. Twenty-First Biennial Conference,
International Council of Kinetography
Laban/Labanotation.
Laban, R., 1963. Modern Educational Dance, Macdonald
and Evans Ltd.
Bartenieff, I. and Lewis D., 1980. Body Movement -
Coping with the environment, Gordon & Breach
Publishers.
Camurri, A., et al., 1999. KANSEI analysis of dance
performance, In Proc IEEE SMC '99.
Nakata, T., 2005. Behaviour Recognition by Temporal
Segmentation, In Proc. 32nd SICE Symposium on
Intelligent Systems.
Mallat, S.G, 1989. A theory for multiresolution signal
decomposition: the wavelet representation, IEEE
Transactions on Pattern Analysis and Machine
Intelligence, vol. 11, Issue 7.
Walker, J.S, 1999. A Primer on Wavelets and Their
Scientific Applications, CRC Press.
Cormen, T.H., et.al. 2001, Introduction to Algorithms,
MIT Press.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
250
