
SIMPLE AND EFFICIENT TOOLS FOR VIRSCULPT
Romain Raffin, Guillaume Thibault, Gilles Gesquière
LSIS, UMR CNRS 6168, ESIL - Case 925, 163 Avenue de Luminy,13288 Marseille, France
Keywords: Virtual sculpting, voxels, deformations, discrete potential fields.
Abstract: Numerous papers are describing methods for virtual sculpture which simulate real behaviours in a virtual
environment. During the sculpture process, the artist does not have to be disturbed by the latency of an
interaction between the object he works on and the tool he uses. Existing data structures or multiprocessing
enhancements are first ways to overcome this problem. We choose to focus our work on the interaction
between an object and a tool in order to improve the modelling process, even if the data model used is kept
simple.
1 INTRODUCTION
Since 1990, a lot of works have been done to
propose to artists an environment for virtual
sculpture. Several interesting functionalities can be
developed: a hard material would become soft; a
reaction process simulate a real one; a material can
be defined with visual or haptic characteristics that
differ from real material; an artist could record an
outline of his work to explore different creative
ways; finally, operation like undo, copy/past would
be interesting.
In the Virsculpt project (Raffin, 2004), our first
goal is to obtain a sculpture environment with no
latency during the interaction between the object and
the tool. The tool definition must also be generic to
permit wide range of sculpting tools. In this paper,
we focused on a volume manipulation methods and
we defined an interaction between tool and object.
Indeed, methods based on surfaces raise
problems if the object topology changes during the
sculpture process (Bill, 1995). Using surface
representation, such as McDonnell’s tri-parametric
Bsplines surfaces (McDonnell, 2001) is not as
intuitive as real sculpting due to the control points
structure.
Several virtual sculpting projects based on
volume models have been developed. First of all, a
volume representation based on CSG can be used,
but the increasing number of operations made during
sculpting process implies a growing computational
time. Such a model has been created by Mizuno to
sculpt virtual wood with an ellipsoidal tool as virtual
chisel (Mizuno, 1999). The two usual CSG
operations (union, intersection) linked to a tool
could be improved with R-functions (Pasko, 2001).
Another volumetric method has been
implemented by Galyean and Hughes (Galyean,
1991); their model is defined with a uniform discrete
spatial enumeration which contains density value.
3D tools modify the discrete potentials which
describe the object. Basic operations like addition or
subtraction, and several tool definitions (heat gun,
sand paper or colour modifier) are proposed.
Using a hierarchical representation decrease the
memory cost of the structure. Bærentzen chooses an
octree which permits to work on higher grid
resolution than uniform enumerations (Bærentzen,
1998). The only tool shape is a sphere, and the
permitted operations are CSG (addition and
subtraction) or surface filter “spray”. Tools are not
using the octree management to obtain an optimized
interaction process. Ferley also works on a
hierarchical organization of voxel to obtain a better
tool-object interaction (Ferley, 2000, 2002). The tool
is limited to an ellipsoid, which is artistically very
restrictive. This last method can be compared to
Kizamu proposed by Perry (Perry, 2001), which uses
distance fields in a discrete space octree. Operations
are CSG on the object or direct triangle face
modifications, but the Euclidean distance field used
instead of density raises discontinuity problems and
increases update computation time.
Simulating material deformation during the
interaction between a tool and an object is important
to obtain a more realistic behaviour. In the range of
436
Raffin R., Thibault G. and Gesquière G. (2006).
SIMPLE AND EFFICIENT TOOLS FOR VIRSCULPT.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 436-440
DOI: 10.5220/0001359104360440
Copyright
c
SciTePress
sculpting methods, we can cite a method using a
spring grid linking the voxels and the diffusion is
made from one voxel to his neighbour, reaching a
stable state (Dewaele, 2004). A similar method,
based on automata cells, is presented by (Druon,
2004 or Arata 1999), the diffusion algorithm uses
artificial intelligence laws to spread matter from a
voxel to one other, but the system still have to reach
a stable state.
Approaches based on discrete potential fields
seem to be interesting because the computation
process does not depend on the number of operation
between tool and object. We denoted that the main
difficulty is to provide adapted tools to the artists.
We can not imagine a traditional sculptor interacting
with unrealistic tools like an ellipsoid or
mathematical functions. Using hierarchical
representation for the object material and the tool is
interesting but the computation process of the
interaction is often expensive and difficult. The
purpose of this paper is to propose a simple but fast
method to deform a voxel-based object. Potential
field values are defined between 0 (the voxel is
empty) and 1 (the voxel is filled). If the value lies in
]0, 1[, the voxel is not completely filled. Material
can be added with a specific tool.
The defined tools will be used in our virtual
sculpting environment (Raffin, 2004). As previously
said, the main goal of this project is to provide a real
time system of interaction on common computers.
Interaction must be realistic and real-time. The
conservation volume aspect is also important. In this
approach, we are developing a set of rapid
algorithms to control and modify a sculpting
environment. We also use the selection of the usable
parts of a tool, as described in (Ayasse, 2000) to
accelerate object/tool collision detection. The first
part of this paper will introduce the diffusion method
of an action in the object. The second part describes
the distribution of the matter. Finally, we present
some images of the deformations and propose some
future works to improve our method.
2 SIMPLE DIFFUSION METHOD
Assuming the collision test between the object and
the tool has been done, we know the tool voxel(s)
that interacts with the object voxel(s). For the
considered object voxel, the matter it contains will
be suppressed. Then, this matter must be propagated
through the object to conserve its volume during
time.
In our method, we propose to displace matter in the
direction of the normal of the voxel tool which is
acting. Whatever the tool’s displacement, when it
reaches the object, we can determine the collided
voxels. If a transformation is applied to the tool, the
representation in the current grid that contains the
object and its environment must be recomputed. It
implies that each transformation of the tool is
embedded in the sculpting grid.
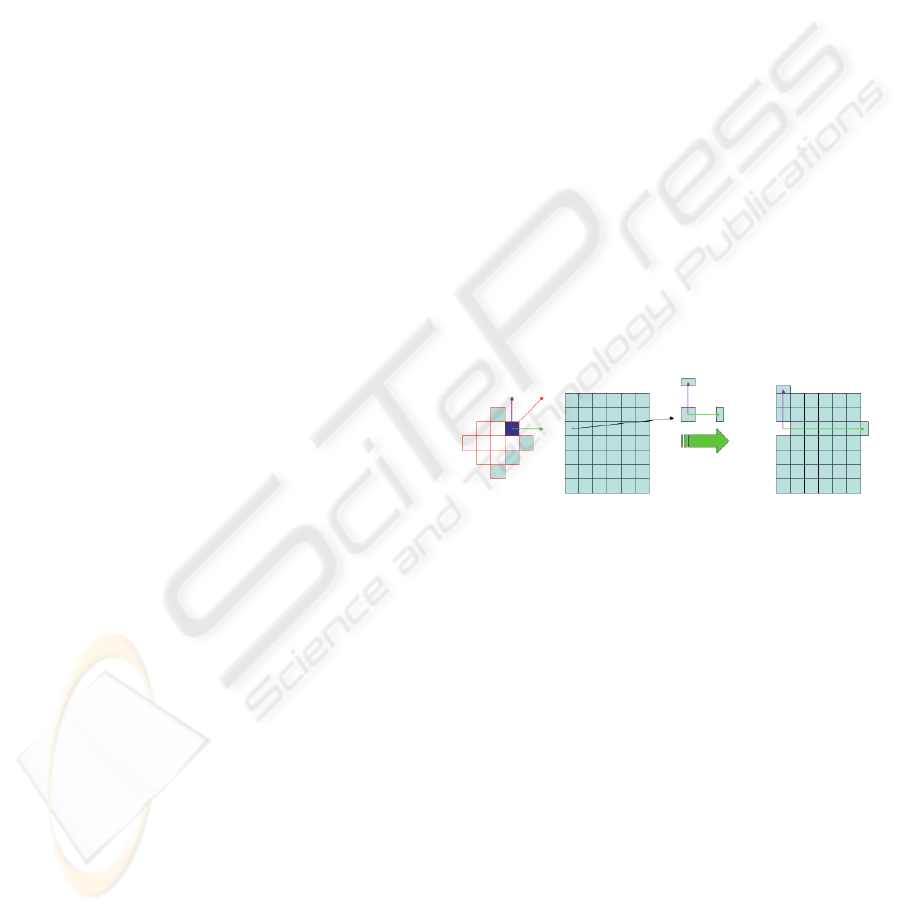
Firstly, we propose to explain our method in a
two dimensions space to avoid confusion (see Figure
1). The object is represented in cyan and is initially a
simple rectangular grid. The tool is an isotropic grid
of 13 voxels represented on the left of the figure.
The tool interacts with voxels of the object and we
focus our discussion on the dark blue voxel of the
tool. Its normal
N
u
ur
, have two components along the
axis (
1
n
u
r
and
2
n
u
ur
), implying
12
Nnn=+
uururuur
. The
corresponding voxel in the object contains an
amount Q of matter that needs to be diffused through
the object. Q is distributed along the axis, which
support the normal components, in q
1
and q
2
, with
Q=q
1
+q
2
.
1
n
u
r
2
n
u
ur
N
u
ur
q
1
q
2
Tool
Object
Matter
repartition
Object
modification
Q
Figure 1: principle of matter diffusion.
To distribute these two parts of Q, we cross the
voxels following the normal components, until a
non-filled voxel is encountered. It says that, if the
initial object is totally filled with matter, the moving
matter q
i
, which came from the collision with the
tool, will be added on a boundary, in the direction of
a normal component. If an encountered voxel have
an amount lesser than the maximum, it is filled until
the quantity q
i
is set to 0.
This method permits to know very quickly if a
voxel on the object surface is receiving matter and
the quantity it would receive. Due to its simplicity, it
does not provide the diffusion in the object (in all
cells of the grid) but towards its surface.
SIMPLE AND EFFICIENT TOOLS FOR VIRSCULPT
437
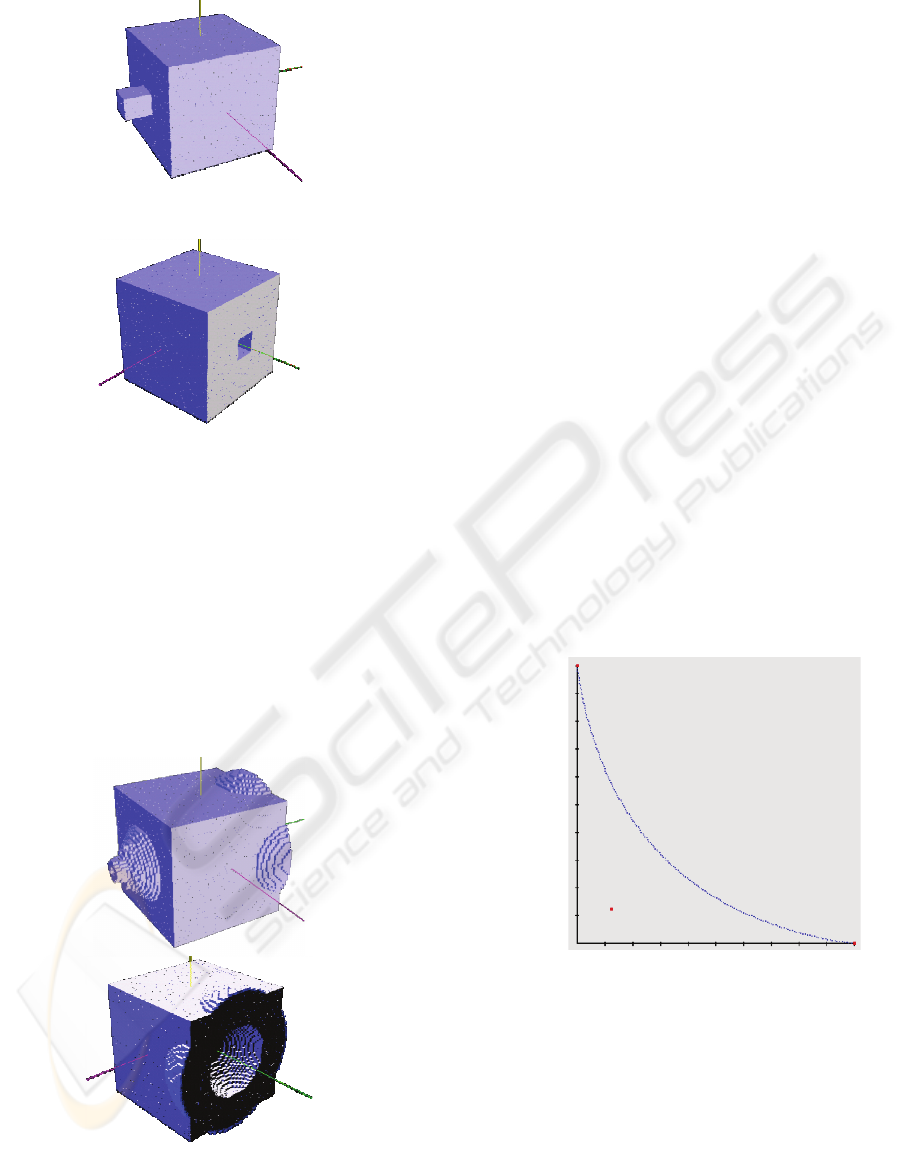
Figure 2: two views of the deformation of an initial
uniform cubic grid, by another cubic tool. The matter
diffusion is not realistic.
As seen on Figure 2, if the tool only contains
voxels in contact with axis oriented normals, the
resulting object seems to be pushed into from a
boundary to the other. On Figure 3, we can see the
same initial object modified by a spherical tool.
While the voxel normals of the tool are directed
radially, the resulting object voxels are pushed in
different directions while the tool enters the object.
Figure 3: two views of the deformation of the initial
uniform cubic grid by a spherical tool.
3 EFFICIENT MATTER
DISTRIBUTION
To perform a more realistic result, we need to
implement the distribution of the exiting matter on
the object surface.
Once the object surface is encountered, adding only
the remaining amount of matter q
i
to one voxel will
result in a poor realistic deformation. We propose
then an algorithm to distribute the matter to surface
neighbours, using a plasticity value of the object
matter. This method is frequently used in free form
deformations to deform the neighbourhood of
constraint points (Raffin, 1999).
We propose indeed to propagate the remaining
matter into a predefined range of voxels, from the
exiting voxel V. Matter repartition is now managed
by a radius of influence R and a repartition function
f. From the exiting voxel V, in the range of R, the
amount q
i
of matter must be distributed. If n
v
voxels
lie in this range, the matter they receive is q
i
/ n
v
.
This first method computes an average of matter
for each influenced voxels. It results in a cylinder at
the surface of the object. On the other hand, we can
use a repartition function as shown at Figure 4 and
the amount of matter decrease from the voxel V to
the voxels out of the range R.
Figure 4: distribution function.
The algorithm of the matter distribution is then:
– First of all, locate the exiting voxel V;
– From V, locate all its neighbours in a range of
influence give by R;
– Compute for each neighbour, the influence
value, depending of its distance to V and the
shape of the distribution function f.
distance
influence
f
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
438

– Affect each influenced voxel v
k
the amount of
matter:
v
k
n
j
j=1
( . influence_value )
influence_value
i
k
q
q =
∑
The effect of the distribution function shape is
represented at Figure 5.
Figure 5: Effect of distribution function f shape. The
distribution can be linear (left) or Gaussian (right).
To construct the distribution function, we use a
Bézier parametric curve, fixing the first control point
as the maximum, when the distance to V is null. The
last control point location implies that the function
value is 0 when the range R is reached. A control
point is let free to be modified interactively by the
user, to create a new function shape.
The images of Figure 6, show the resulting
object obtained with this method, using a cubic tool,
with two distribution functions. On the Figure 7, the
tool applied is a star-shaped tip, with viscosity
enabled or not.
4 CONCLUSION AND FUTURE
WORKS
The model we presented is admittedly simple but
rather efficient to provide rapid sculpting method.
For example, we act on a 50x50x50 grid with less
than 1/10th of a second to compute and roughly
render on a basic PC (Pentium 4 class, 512 Mo,
2Ghz CPU, with no GPU acceleration). As we said
previously, we deliberately do not use powerful data
structures to focus on the deformation method. The
complexity of global diffusion algorithm is
decreased by the use of normal components. The
realism of the deformation is only computed at the
object surface.
Using voxels seems to be a good way to obtain
real-time interaction. To increase the number of
voxels, we plan to use a paging method. We will
only use a partial part of the object. If we have time,
we can load other parts “on the fly”.
We also plan to improve our model by taking into
account the tool displacement direction when
striking (actually, the direction displacement is
perpendicular to the face of the object).
Indeed an important work would be made on the
reaction of the matter, using viscosity to provide
creases, bulges and matter crushing as, for example,
if the object is lying on a rigid table.
Figure 6: the two upper images show a deformation with a
cube, with different distribution functions. The last image
is the same spherical tool that the one used in Figure 3.
SIMPLE AND EFFICIENT TOOLS FOR VIRSCULPT
439

Figure 7: three views of a cube pushed into by a star-
shaped tip. The two first images are made without
viscosity and the down image use a high viscosity
value.
REFERENCES
Arata, H., Takai, Y., Takai, N.K.and Yamamoto, T., 1999.
Free form shape modelling by 3D cellular automata.
International Conference on Shape Modeling and
Applications, pp. 242-247, 1999.
Ayasse, J. and Müller, H., 2000. Sculpturing on discrete
displacement fields. Comput. Graph. Forum, 21(3).
Bærentzen, A., 1998. Octree-based volume sculpting,
Presented at IEEE Visualization ‘98.
Bill, J.-R. and Lodha, S., 1995. Sculpting polygonal
models using virtual tools, In Graphics Interface’95,
pp. 272-278.
Dewaele, G., and Cani, M.P., 2004. Interactive global and
Local Deformations for Virtual Clay, Graphical
Models (GMOD), vol. 66, pp. 352-369.
Druon, S., 2004. Modélisation et recalage d’objets et
d’environnements en déformation viscoplastique :Aide
au geste pour les métiers matière, PhD thesis (in
french), University of Montpellier, Lirmm.
Ferley, E., Cani, M.P., and Gascuel, J.D., 2000. Practical
Volumetric Sculpting, The Visual Computer,
8(16):469-480
Ferley, E., Cani, M.P. and Gascuel, J.D, 2002. Resolution
adaptive volume sculpting, Graphical Models
(GMOD), 63:459-478, special issue on Volume
Modelling.
Galyean, T. and Hughes, J., 1991. Sculpting: An
interactive volumetric modeling technique, Computer
Graphics, 25(4):267-274. Proceedings of Siggraph’91.
McDonnell, K.T, Qin, H. and Wlodarczyk, R.A, 2001.
Virtual Clay: A real time sculpting system with haptic
toolkits, Proceedings of the 2001 ACM Symposium on
Interactive 3D Graphics, pp. 179-190.
Mizuno, S., Okada, M., and Toriwaki, J.I., 1999. An
interactive designing system with virtual sculpting and
virtual woodcut printing, Comput. Graph. Forum,
18(3):183-194.
Pasko A, Savchenko V, and Sourin A., 2001, Synthetic
carving using implicit surface primitives. Computer
Aided Design, 33(5):379-388
Perry, R.N. and Frisken, F. S., 2001. Kizamu: A system
for sculpting digital characters, Proceedings of
SIGGRAPH 2001, pp. 47-56, ISBN 1-58113-292-1.
Raffin, R., Neveu, M., and Jaar, F., 1999. Extended
constrained deformations: a new sculpturing tool, in
International Conference on Shape Modeling and
Applications, University of Aizu, Japan, pp. 219-224,
IEEE Computer Society.
Raffin, R., Gesquière, G., Remy, E. and Thon S., 2004.
VirSculpt: a virtual sculpting environment, GraphiCon
04, pp. 184-187, Moscow.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
440
