ON COLOUR SPACES AND ON COLOUR PERCEPTION

Independence between uniques and chromatic circularity

Alfredo Restrepo Palacios

Laboratorio de Señales, Dpt. Ing. Eléctrica y Electrónica, Universidad de los Andes, Bogotá, Colombia

Keywords: Colour space, unique colour, spectral colour, independence of uniques, chromatic circularity.

Abstract: The colour space one uses has a bearing on the type of colour image processing tasks one does. As we

approach the stage of colour processing in image processing, new colour spaces may be needed. In

particular, colour spaces that model properties of our perception of colour may be useful. We propose two

nonlinear, tridimensional transformations of the variables of the RGB (or LMS) colour space. In the

resulting spaces pure S, or pure M input, does not imply the presence of yellow. Since there is evidence of S

input to the parvocelular system, we use a dimension called violet minus green; in the resulting space, as the

wavelength variable sweeps the visible spectrum, a circle is obtained, making explicit a circularity of

chromaticity for spectral colours.

1 INTRODUCTION

While experimenting with a technique for colour

contrast enhancement (Restrepo et al, 2002),

(Restrepo and Vega, 2005), for which colour space

is triangulated with tetrahedra and points (colours)

within each tetrahedron are expanded, it became

clear that the technique performs better in some

colour spaces than in others. In particular, for the

detection of malaria parasites in thin blood films, the

colour space called here Hering-2 is better than

traditional RGB space (Ortiz et al, 2005).

We are particularly interested in perceptually

good colour spaces. In RGB space, the corners of

the cube although geometrically equivalent, play

different roles perceptually: cyan and violet are

binary colours, black and white are achromatic

colours while red, green, blue and yellow are unique

colours. We say that a colour space is perceptually

better than another if it geometrically makes

conspicuous perceptual aspects and does not

geometrically differentiate between aspects that

perceptually are of the same type. The terminology

used here and that includes the terms unique colour

and binary colour is the one used by researchers

such as Pridmore, in (Pridmore, 1999).

Trichromacy, although a fundamental link

between the wavelength and the perceptual aspects

of colour, is also a source of misunderstanding,

partially because it is valid both at the receptoral

(e.g. in the human retina or in a colour camera) and

at the stimulus (MacAdam, 1985) (e.g. in a colour

projector or a computer screen) levels. At a

receptoral level, it is convenient to call the response

variables of the human visual system large, medium

and small, rather than red, green and blue, the terms

red, green and blue being misleading there.

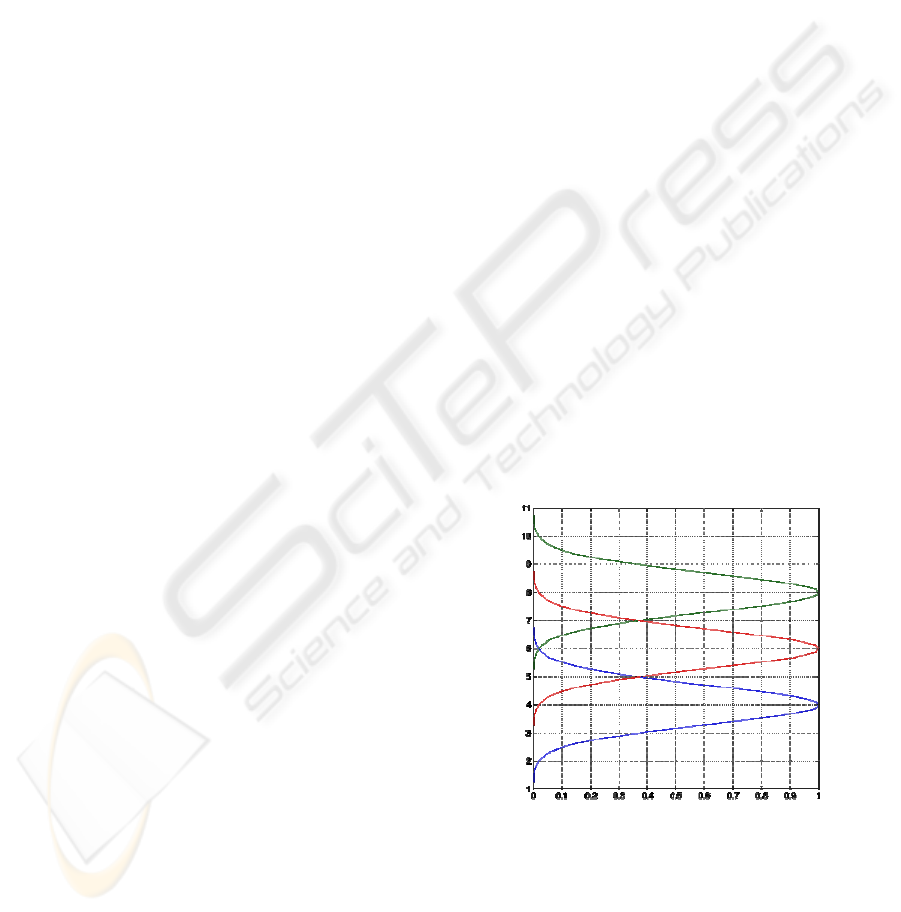
Figure 1: Assumed R, G and B functions. For the purpose

of a schematic illustration of the ideas presented here, for

the R, G and B functions, we use the shown bell shaped

curves, on an artificial wavelength scale from 0 to 12,

rather than real curves based on psychophysical data.

Likewise, in image processing, RGB is an

ambiguous term, partly because of the phenomenon

of metamerism. Interpreted as an input code for

image processing, RGB refers to the broadband and

183

Restrepo Palacios A. (2006).

ON COLOUR SPACES AND ON COLOUR PERCEPTION - Independence between uniques and chromatic circularity.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 183-187

DOI: 10.5220/0001361201830187

 SciTePress

overlapping functions R(λ) (a high-pass filter at

approximately 600 nm) G(λ) (a band-pass between

approx. 500 and 575 nm) and B(λ) (a low-pass at

approx. 500 nm), of the wavelength variable λ,

which are the spectral transmittance functions of the

3 filters used in colour cameras. As an output code,

RGB may refer to the relative intensities of three

light sources of narrow spectrum (e.g. a Blue Violet

LED at 430 nm, a Super Red LED at 633 nm and a

Pure Green LED at 555 nm) which when combined

evoke the corresponding same RGB readings in a

colour camera; these narrowband lights do not

usually have the colours we speak of as red, blue and

green. Unique red is not a spectral colour, in fact,

unique red, a red that does not appear neither

yellowish nor bluish must include both long and

short wavelengths [4]. When displaying colours on

the screen of the computer, RGB values given by 1

0 0, 1 1 0, 0 1 0 and 0 0 1 correspond to “pure” red,

yellow, green and blue, respectively, and if we want

pure and unique coincide, the stimulus

corresponding to red cannot be narrow band.

The NCS (Natural Colour Space) is inspired in

Hering´s colour theory of opposite colour pairs

(Hering, 1964), advanced towards the end of the

nineteenth century and rechampioned by Hurvich

and Jameson (Hurvich and Jameson, 1957). The

dimensions in NCS space are red versus green or

RG, yellow versus blue or YB and lightness or

Bk&Wt. As a system inspired in the opposing colour

theory, the four chromatic basic components given

by [RG, YB, Bk&Wt] = [1, 0, 1/3], [-1, 0, 1/3], [0, 1,

1/3] and [0, -1, 1/3], should correspond to unique

colours. An interesting asymmetry should be noted

here: the two chromatic and opposing processes RG

and YB differ in that a mixture of green and red is

likely to produce a yellow, which lies in the

chromatic YB dimension, while a mixture of blue

and yellow is likely to produce a grey, in the Bk&Wt

dimension, with no chromatic RG or YB component.

(A mixture of binaries cyan and violet is likely to

produce a grey, though.) Also, the chromatic RG and

YB processes are opposing from the perceptual point

of view, while the achromatic Bk&Wt process is a

cooperative process: greys are perceptually

intermediate colours between black and white.

At the perceptual level there is an independence

between the uniques green, red, yellow and blue; the

four “true colours” proposed by Alberti in 1435

(www.colorsystems.com, 2005). (Also interesting,

perceptually, there are four chromatic binaries, and

no “ternary” chromatic combinations.) We would

like a colour system that allowed such an orthogonal

quality between uniques, and have the possibility of

zeroing e.g. the RG channel but not the YB channel.

(Clearly, there should be no way of silencing the

achromatic, magnocelular system.) Such an

independence does not exist for the dimensions of

the RGB system as the response curves overlap.

Even though the NCS system is perceptually a better

model than RGB space, granting that the NCS and

RGB systems are linearly related as RG = R-G, YB

= 0.5(R+G)-B and Bk&Wt = (1/3)(R+G+B), NCS

space has the apparent drawback that from pure red

and from pure green, a nonzero yellow results: YB =

0.5. This is a source of confusion since we might

expect an independence between the Y part of the

YB dimension of the NCS colour system and the RG

dimension, all of the involved colours red, green,

yellow and blue being uniques.

The workings of a color camera model the

responses of the human L, M and S channels, at the

receptoral level. Pioneered by Young, polished

during the nineteenth century by Maxwell and

Grassmann and finally published in complete form

by Helmholtz (Helmholtz, 2005), the Young-

Helmholtz trichromacy theory served as an

inspiration for the color TV camera. However, the

perceptual uniques red, yellow, green and blue,

result from (possibly multiple, accounting for

metamerism,) specific combinations of the L, M and

S responses, and not from only one of these channels

responding at a time. Not even at the ganglionar

level, where Hering´s theories found biological

grounds, are the uniques made explicit (as Marr

would say (Marr, 1980)) by a unique channel system

of firing neurons. The NCS system and the

architecture of the human visual system correlate at

the ganglionar level like this: the RG dimension

corresponds to the parvo system of the human visual

system, the YB dimension to the konio system and

the Bk&Wt dimension to the magno system. It is

perhaps not until cortical area V4 that a 1-1

correspondence between our colour experience and

the responses of specific neurons is found (Zeki,

1993).

It will be probably necessary to go beyond the

RGB and NCS colour systems to do meaningful

colour processing of images. At any rate, this path

roughly follows the course of the visual system in

frugivorous primates; RGB correlates with the

receptoral layer of the retina while NCS correlates

with the ganglionar layer.

In this paper, guided by the search of

mathematical models of the circular perception of

chromaticity and of the independence of the uniques

red and green and the unique yellow, we propose

two colour systems; the starting point being the

RGB system

VISAPP 2006 - IMAGE UNDERSTANDING

184

2 THE TRIDIMENSIONALITY OF

COLOUR PERCEPTION

Aristotle´s model of colour is linear (Aristotle,

2001), (Aristotle, 2002), as it is da Vinci’s (da Vinci,

2002). Although Acuilonius in the fifteenth century

proposed a model that is not linear and includes

black and white as extrema, the first circular model

of (chromatic) colour is Newton´s circle of colours,

which appears in his work Optiks in 1704. In 1810,

Otto Runge published his sphere of colours, the first

tridimensional colour space, from a geometric point

of view (www.colorsystem.com, 2005). The

mathematization of trichromaticity by Grassmann

gave the algebraic tridimensionality to trichromatic

colour space. Hering´s opposing colour theory is

also tridimensional; likewise, colour space HSI

(Hue, Saturation, Intensity) is tridimensional.

Granting that a colour space should be

tridimensional and even if in all currently accepted

cases, topologically the space is a 3-ball, the fact

remains that there are many possible tridimensional

manifolds. And it is not clear whether they should

have a boundary: no matter how white a region in a

scene looks, it is possible to make another region

look whiter. Also, other mathematical structures

(such as orbifolds), besides manifolds could turn out

to be more appropriate.

Besides the geometric and topological properties

of a colour space, there should be also algebraic

structures modelling of colour mixtures and colour

independence. We are well behind such

expectations; consider for example that the RGB

cube is not closed under the operation of standard

vector addition

3 INDEPENDENCE BETWEEN

RED, GREEN AND YELLOW

In the NCS space, both pure yellow (RGB=110) and

pure blue (RGB=001) result in a zero valued RG

channel; not so for pure red and pure green when

considering the YB channel. We propose a

modification of the YB dimension of the NCS

consisting in modulating it with the factor (R*G –

B), which we interpret as red and green, or blue.

This makes the new variable Y\B zero, for pure red

and for pure green; we call the resulting

transformation Hering-1

RG = R – G

Y\B = (R*G + B)(0.5[R + G] - B) (1)

Bk&Wt = (1/3)(R + G + B)

The resulting image of the RGB cube, under

transformation (2), is shown in Fig. 2.

E.g. for R= 0, the equation for the surface image

of the plane G-B is given by

Y\B = [3/2]*(Bk&Wt)

– (3/8)*RG

*Bk&Wt

For the computation of the inverse of

Transformation 2, we must first solve the cubic

polynomial in the variable B

+ (4 – 7*Bk&Wt)*B

+ (15*Bk&Wt

– 4*Bk&Wt-RG

)*B

+ Bk&Wt*RG

– 9*Bk&Wt + (3/8)*YB = 0

and then solve for R and G

Figure 2: The image of the RGB cube under

Transformation (2).

R = 0.5(3*Bk&Wt + RG – B)

G = 0.5(3*Bk&Wt – RG – B).

Several researchers have remarked on the need

for nonlinear models of the L, M and S variables for

colour perception. (Larrimer, 1974), (Elzinga and

de Weert, 1984); so, it is not unreasonable to use

nonlinear transformations for colour spaces in image

processing

4 CIRCULARITY

Let us remind ourselves that there are non spectral

colours; that is, colours that are not metameric to

any narrowband spectral light, among them we have

the greys, browns (which result mainly in contrast)

and unique red (in fact, the whole line of purples of

CIE space).

As the wavelength of a hypothetical single-

wavelength light (a spectral light) sweeps the visible

ON COLOUR SPACES AND ON COLOUR PERCEPTION - Independence between uniques and chromatic circularity

185

spectrum, the resulting point in RGB space (using

the functions in Fig. 1) describes a curve as the one

shown in Fig. 3, that starts at the origin (pure black),

parallel to the B axis and ends at the origin, parallel

to the R axis. On the other hand, since unique red is

not a spectral colour, a curve of visible λ’s in a

hypothetical perceptual colour space would not be a

simple closed curve (i.e. a topological circle), there

would be a gap between spectral colours

corresponding to large wavelengths which we

perceive as reddish oranges and those of small

wavelengths which we perceive as purples. Our aim

here is to have a colour space where such a curve

corresponding to spectral lights is closed and closes

itself at a point where the variables R and B are

small valued but not yet zero. (It is probably

incorrect to assume that an electromagnetic radiation

with spectral contents off the

visible spectrum gives

rise to black; invisible would be a more appropriate

term.)

Figure 3: The image of the wavelength interval [2, 10]

with respect to the functions R, G and B of Figure 1

In order to speak of a curve in a hypothetical

colour perception space we need the mathematical

concept of continuity. The perceptual correlate of

such a continuity is grounded in MacAdams´ ellipses

(MacAdam, 1999). His finding gives geometrical

meaning to the fact that a small enough change in

the spectral contents of a light goes unnoticed; it

gives fuzziness to the concept of equivalence in

colour space.

A new transformation, called Hering-2 is

obtained by further transforming the variables Y\B

and RG of the Hering-1 colour space. As has been

pointed out (Stromeyer et al, 1998), there may well

be an input from the S channel to the parvo channel;

thus, instead of a red-versus-green process, we

propose a violet. versus. green process given by

V~G= 0.5(R+B) – G

In addition, modulating the YB variable of the

NCS system with red or blue, and green, we also get

zero for pure green and for pure red, in a new

variable called Y~B. We get circularity for spectral

colours in this way.

Y~B = 10G(R+B)(0.5[R + G] - B)

A factor of 10 has been added to make clearer

the resulting circularity in a plot. Thus, we have the

transformation Hering-2 given by

V~G= 0.5(R+B) – G

Y~B = 10G(R+B)(0.5[R + G] - B) (2)

Bk&Wt = (1/3)(R + G + B)

Figure 4: The image in the V~G – Y~B plane of the

wavelength interval [0, 12] with respect to the functions R,

G and B of Figure 1

Under this transformation, in the V~G – Y~B

plane, the curve corresponding to the spectral lights,

for the interval λ∈[0, 12], is as shown in Fig. 4; a

closed curve is obtained. The curve in Fig. 4 is not

meant to include black, (the origin) as the curve

closes on itself before the three variates R, G and B

are all zero.

To invert (3), we obtain B, using a rational

function, then we find R and G, as shown below.

*YB − 9*Bk &Wt

+ 2*VG

* Bk &Wt + 30 * VG * Bk &Wt

3*VG * Bk &W

−

9Bk &W

+ 2VG

VISAPP 2006 - IMAGE UNDERSTANDING

186

R= 3*Bk&Wt + (2/3)*VG – B

G= Bk&Wt – (2/3)*VG

6 CONCLUSION

Two transformations of the R, G, B data, intended to

model the perceptual independence between unique

colours, and the perceptual circularity of our colour

perception, up to spectral colours, are given. As the

perceptual properties are surely advantageous to

frugivory primates, it is probable that the given

implementations will be of use in computer vision,

they have shown to be useful in the detection of

malaria in images from thin blood films. We have

explored colour standardization by triangulating

colour space and expanding colours within each

tetrahedron (Restrepo et al, 2002), for the

recognition of malaria (Ortiz et al, 2005), we had

that Hering-2 is a more meaningful space.

Regarding the perceptual independence between

reds and greens on the one side and yellows on the

other, it probably has advantages regarding the

detection of mature fruits. It is difficult to speculate

as to the ways and advantages in which circular

chromaticity is achieved in the human visual system;

for one thing, it is probably not convenient to have

to close a chromatic circle using black; a symmetry

in the way the L, M and S channels are treated by

the neural circuits of the visual system may

represent savings ins genetic code and neural wiring.

Unlike NCS space, in RGB space the achromatic

line is not geometrically conspicuous in the cube and

it is hard to speak of the circularity of the chromatic

colours.

Colour, as a perceptual entity is meant to give us

information about the surfaces of the objects in a

scene and, as such, is largely independent of the

spectral contents of the illuminant. Even though

mathematically, pointwise, colour is a vector

statistic of a spectral density, it is a very

sophisticated measure when taken in the context of

the surrounding colours in a scene. We can only try

and speculate about the adavantages brought about

by the workings of our visual perception.

ACKNOWLEDGEMENTS

We would like to thank the anonymous reviewers of

a cruder version of this paper for their patience and

much valuable comments

REFERENCES

Restrepo, A., Nieto, A., Ardila, S. and Vega., J., 2002. An

approximation to color standardization. In Procs. 4

IASTED Signal and Image Processing Int. Conf.

Kawai, 609-614.

Restrepo, A. and Vega, J., 2005. A Tool for Color

Contrast Enhancement. In Memorias del X Simposio

de Tratamiento de Imagenes, Señales y Visión

Artificial, Cali, Colombia.

http://senales.univalle.edu.co.

Ortiz, M.V., Pimentel, M.A. y Restrepo, A., 2005.

Metodología para el reconocimiento automático de la

malaria basado en color. In Memorias del X Simposio

de Tratamiento de Imagenes, Señales y Visión

Artificial, Cali, Colombia.

http://senales.univalle.edu.co

Pridmore, R.W., 1999. Unique and binary hues as

functions of luminance and illuminant color

temperature, and relations with invariant hues. Vision

Research, 39, 3892-3908.

MacAdam. D.L., 1985. Color Measurement, Theme and

variations, Springer, Berlin, 2

edition.

Hering, E., 1964 Outlines of a Theory of the Light Sense.

Tr. by L. M. Hurvich and D. Jameson, Harvard

University Press, Cambridge.

Hurvich, L.M. and Jameson, D., 1957 An pponent-process

theory of color vision Psychological Review, 64, 6,

385-403.

www.colorsystem.com, 2005

Helmholtz, von H., 2005. Treatise on Physiological

Optics,. Dover, Mineola.

Marr, D., 1980. Vision. Freeman, San Francisco.

Zeki, S., 1993. A Vision of the Brain. Blackwell, Oxford.

Aristotele, 2001. Anima. Bompiani, Milano.

Aristotele, 2002. L’anima e il corpo. Parva Naturalia.

Bompiani, Milano.

da Vinci, L., 2002. Trattato della pittura. Rusconi, Roma.

Larimer, J., 1974. “Opponent-process additivity -I:

Red/Green equilibria. Vision Research, 14, 1127-

1140.

Elzinga, C.H. and de Weert, C.M.M., 1984. Nonlinear

codes for the yellow/blue mechanism. Vision

Research, 24, 911-922.

Macadam, D.L, 1999. Role of luminance increments in

small color differences. In Color Metrics, J.J. Vos,

L.F.C. Friele and P.L. Walraven, eds., 160-167.

C.F. Stromeyer, C.F., Chaparro, A., Rodriguez, C., Chen.

D., Hu, E. and R.E. Kronauer, R.E., 1998. Short-wave

cone signal in th Red-Green Detection Mechanism.

Vision Research 38, 813-826.

www.microbackup.magnet.fsu.edu/primer/lightandcolor/le

dsintro.html, 2005.

ON COLOUR SPACES AND ON COLOUR PERCEPTION - Independence between uniques and chromatic circularity

187