AUTOMATIC EXTRACTION OF CLOSED CONTOURS IN THE

PORTUGUESE CADASTRAL MAPS

Tiago Candeias, Filipe Tomaz, Hamid Shahbazkia

Universidade do Algarve, Computer Science Laboratory

Campus de Gambelas, 8000-117 Faro, Portugal

Keywords:

Contour Extraction, Image Recognition, Document Image Analysis.

Abstract:

The automatic extraction of closed contours is the most important and difﬁcult problem in the automatic recog-

nition of the Portuguese cadastral maps. Many difﬁculties such as gaps on contour, elements connected on

contour, crossing of lines and the association of each entity to its contour have to be solved. In literature there

are very few studies about the recognition of cadastral maps and the maps already studied are different than

ours. Therefore our research mainly focused on appropriate computer vision algorithms that yield acceptable

results.

In this paper we present a sequence of algorithms to solve various problems in the contour extraction. The

algorithms are completely different and each one tries to solve one speciﬁc problem of the analysis. The

methods used were the Block-Fill algorithm, the Lohmann’s algorithm, the Seed-Segment algorithm and the

Rosin-West’s vectorization algorithm.

The architecture of our system is presented and the results are shown at the end of the paper.

1 INTRODUCTION

The automatic digitalisation of the Portuguese cadas-

tral maps has many problems and difﬁculties that rep-

resent interesting challenges in the image recognition

ﬁeld. One of those problems and certainly the most

difﬁcult is the automatic extraction of the closed con-

tours. These difﬁculties are due to the quality of im-

ages to recognise and the way the maps were drew.

These cadastral maps are composed by many dif-

ferent patterns such as crosses, circles, arcs, dashed

lines, solid lines and characters. Each pattern has

a semantic, for instance a circle represents a cadas-

tral entity, which is inside of a closed solid line that

represent the parcel’s contour and deﬁnes the con-

tour perimeter. Perhaps a parcel has inside some

dashed lines and some characters that represent the

sub-parcel’s contour and the sub-parcel’s type or sub-

parcel’s number.

The automatic extraction of the closed contours in

this type of maps has many difﬁculties namely gaps in

contour, elements connected on contour and also the

crossing of lines on contour (see ﬁgure 1). Further-

more, it is necessary to associate each parcel using

the circle position with its closed contour.

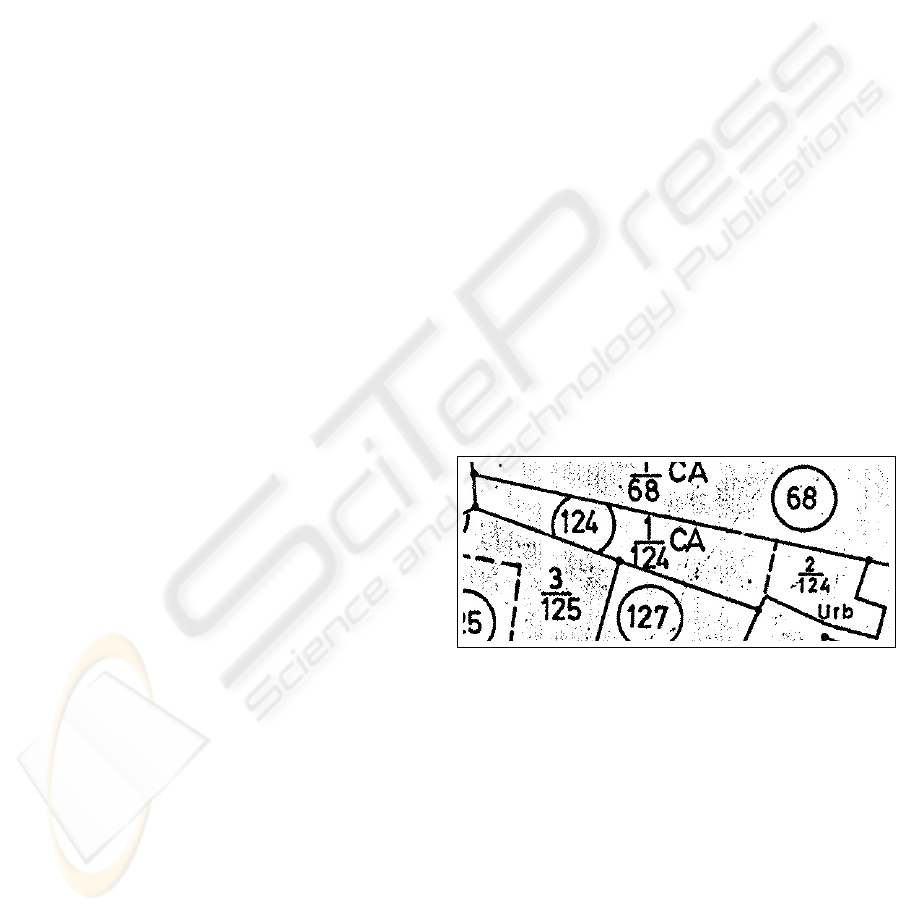
Figure 1: Examples of some problems in the contour extrac-

tion such as gaps in contour, elements connected on contour,

the crossing of lines and also it is needed to associate a cir-

cle with a contour.

In the literature, there is not any algorithm which

could solve all of these problems, but only simple

methods that can individually solve one problem.

Therefore, we use one algorithm to solve each prob-

lem, instead of trying to design a complex method to

ﬁx all of them.

428

Candeias T., Tomaz F. and Shahbazkia H. (2006).

AUTOMATIC EXTRACTION OF CLOSED CONTOURS IN THE PORTUGUESE CADASTRAL MAPS.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 428-433

DOI: 10.5220/0001361304280433

 SciTePress

2 RELATED WORK

The image recognition problem can be seen on two

different perspectives, considering the pattern recog-

nition at pixel level or using segments from the vec-

torisation process. Those approaches can recognise

the graphical primitives in image but each one has

speciﬁc problems. Song et al. (Jiqiang Song and Cai,

2002b) discussed the recognition from binary images

using each one of these approaches, and they sug-

gested to use both, since neither of them is perfect

enough to handle all the difﬁculties.

The image recognition at pixel level should be

analysed in a hierarchic point of view, recognising the

features of the drawings from the simplest to the most

complex primitive. Song et al. (Song et al., 2002) con-

sidered that an engineering drawing can be seen as a

collection of lines, arcs, curves, simbols and strings.

In each recognition process the elements detected are

erased or segmented to simplify the next detections.

Dori and Wenyin (Dori and Wenyin, 1999) have

developed a vectorisation system for the mechanical

drawings, ﬁrstly doing a description of the image by

segments and detecting higher shapes as circles or

arcs later. But as our maps have elements connected

on contour, a vectorisation and followed by the recog-

nition of shapes would introduce many errors. There-

fore our choice was to analyse the image at pixel level

since it is less complex even though slower (Tombre

et al., 1999).

Song et al. (Jiqiang Song and Cai, 2002a) stud-

ied the vectorisation of engineering drawings at pixel

level and Dosch et al. (Dosch et al., 2000) studied a

system for the recognition of architectural drawings.

The French cadastral map is a completely differ-

ent sheet because it is older and has others types

of problems, Shahbazkia (Shahbazkia, 1998) studied

the recognition of the French cadastral maps. Also

Viglino et al. (Jean-Marc Viglino, 2003) are studying

the contour extraction in the French cadastral map.

The knoweledge on the Portuguese cadastral maps

(analysis domain) is available and we can use it to

simplify the contour extraction.

3 PROCESSING METHODS

The main stages of the cadastral maps recognition are

the detection of circles, the parcel’s number recog-

nition and the contour extraction. Since any parcels

have a contour associated, so the contour extraction

algorithm has as input the circle position to allow the

association with the contour.

The deformation of the image introduces noise and

degradation, and it is going to yield dirt and gaps

in the drawings. The cadastral maps have symbols,

dashes and circles over the contours as well. This su-

perposition difﬁcults the extraction very much since it

is necessary to segment the two elements ﬁrst.

It is important to deeply look for each problem of

the contour extraction to choose the algorithms that

can solve them. The main difﬁculties of this analy-

sis are the discontinuities, the elements connected and

the crossing of contour lines. The application of the

line following algorithm (Spinello and Guitton, 2004)

with waiting lists is very complex in the last situation

due to the variety of paths to follow. Furthermore the

line following algorithm does not solve the problem

of elements connected on contour, the association of

each parcel to the contour and neither the discontinu-

ities on it.

In the literature there is not any general method

solving all these problems, however for each problem

there is some possible solution. We chose that each

method had to solve one speciﬁc problem since we

think this improves the robustness of the application

and makes it simpler. Each algorithm has different

features and properties and all of them enable us to

solve most of the difﬁculties.

3.1 Block-Fill Algorithm

From the beginning, we tried to ﬁnd out an off-the-

shelf method (Tombre et al., 1998) to implement the

contour extraction. Our ﬁrst idea was to use the classi-

cal snakes algorithm (Kass et al., 1987) but as it needs

some control points and it did not always converge

due to the lack of grey value in image, we did not use

it.

As the method can start the analysis from the circle

position, the ﬂood ﬁll algorithm sounded better. As

some contours have gaps, we implemented an algo-

rithm based on the ﬂood ﬁll but using blocks. The in-

put image is pre-processed by a thinning (Tombre and

Tabbone, 2000) to detect the central contour points

since it is necessary to have the same segment be-

tween two neighbors contours.

The block ﬁll algorithm starts the detection at the

circle position and ﬁlls the parcel with blocks of size

NxN. This algorithm is iterative, in the ﬁrst iteration

the stack has only the circle position, in the second

the ﬁrst block’s 4-neighbors if the blocks have not any

black pixel inside, the algorithm continues the ﬁlling

looking for the neighbor blocks (see ﬁgure 2).

The detection of the contour points is done con-

sidering the blocks that touch on the contour. Each

block has neighbor blocks outside of the contour and

they were tested in every directions to detect every

contour points. The goal is to detect as many points

as possible, however as there are parts of the contour

where it is impossible to detect all the points, it is nec-

essary to use a method of line following to detect the

contour points that are between the two parts already

AUTOMATIC EXTRACTION OF CLOSED CONTOURS IN THE PORTUGUESE CADASTRAL MAPS

429

(a) The initial image of a

closed contour.

(b) The block ﬁll algo-

rithm in the thinned image.

Figure 2: Example of the block ﬁll algorithm application.

detected. The line following algorithm is applicable

since we used a thinning of the contours and without

the non connected elements resulting in the contour

lines with one pixel width.

The block ﬁll is the kernel of the contour extraction

and the next algorithms were implemented to solve

some problems of this algorithm.

3.2 Lohmann’s Algorithm

The ﬁrst problem of the block ﬁll algorithm is that

some blocks go out of the contour due to the large dis-

continuities. For instance, a large discontinuity can

appear when two small discontinuities are close, af-

ter segmenting the bigger from the smaller elements

(component labeling algorithm) the element between

the two discontinuities is erased. The goal of the

Lohmann’s algorithm (Lohman, 1995) is to segment

the inner contour that is open and has large disconti-

nuities.

Before applying the Lohmann’s algorithm, it is

necessary to have the distance transform (di Baja,

1994) of the thinned contour image. As the block ﬁll

algorithm, this also has as input a point inside of the

contour. This algorithm is iterative and starts pushing

the input point into the stack. Following, the point of

the stack’s head is popped and from this position is

found out the maximum circle radius that touchs the

contour points. The algorithm then detects the local

maximums over the maximum circle radius and store

them into the stack. Once a circle is accepted as be-

ing inside of the contour, if there is not any end point

in the circle radius, then the points inside of the cir-

cle are painted with the black color in the distance

transform image to enable the convergence of the al-

gorithm. This process repeats until the maximum cir-

cle radius has a discontinuous point of the contour (a

point with only one neighbor), so the gap length is

calculated and if the circle is outside of the contour or

the gap length is bigger than a threshold value, then

is not considered, otherwise the expansion continues

and the maximum locals of the circles are pushed into

the stack.

(a) The blocks goes out-

side using the block ﬁll al-

gorithm.

(b) The circles of the

Lohmann’s algorithm do

not go outside.

Figure 3: Example of the Lohmann’s algorithm behavior

with big discontinuities.

This process continues until the stack is empty. At

the end, the contour is ﬁlled with circles of different

sizes (see ﬁgure 3) allowing to segment the inner con-

tour.

After getting the list of circles that segment the con-

tour, we can only consider the blocks from the block

ﬁll algorithm that are inside of at least one of these

circles. Therefore we can use the block ﬁll algorithm

to detect only the points inside of the contour even

having big discontinuities.

3.3 Seed-Segment Algorithm

Another problem happens when the symbols are con-

nected on the contour. A consequence of this fact is

that the parcel’s contour is empty or incomplete after

the application of the block ﬁll algorithm. One pos-

sible solution is ﬁrst segment the symbols from the

contour using a straight line detection algorithm such

as the hough transform algorithm (Jiqiang Song and

Cai, 2002c) but after some tests this algorithm did not

solve our problems since there are some curves in im-

ages.

A seed segment is a small rectangle with any ori-

entation that is characteristic of a straight line and it

is found considering some conditions. The seed seg-

ment algorithm (Song et al., 2000) starts looking for

seed segments in the image. This method detects the

straight lines in the image doing the line tracking from

the seed segment orientation.

Knowing some contour straight lines, it is easy to

segment the symbols from the solid line. The ﬁgure 4

shows an element connected to the contour, but after

the application of the line tracking, it is possible to de-

VISAPP 2006 - IMAGE ANALYSIS

430

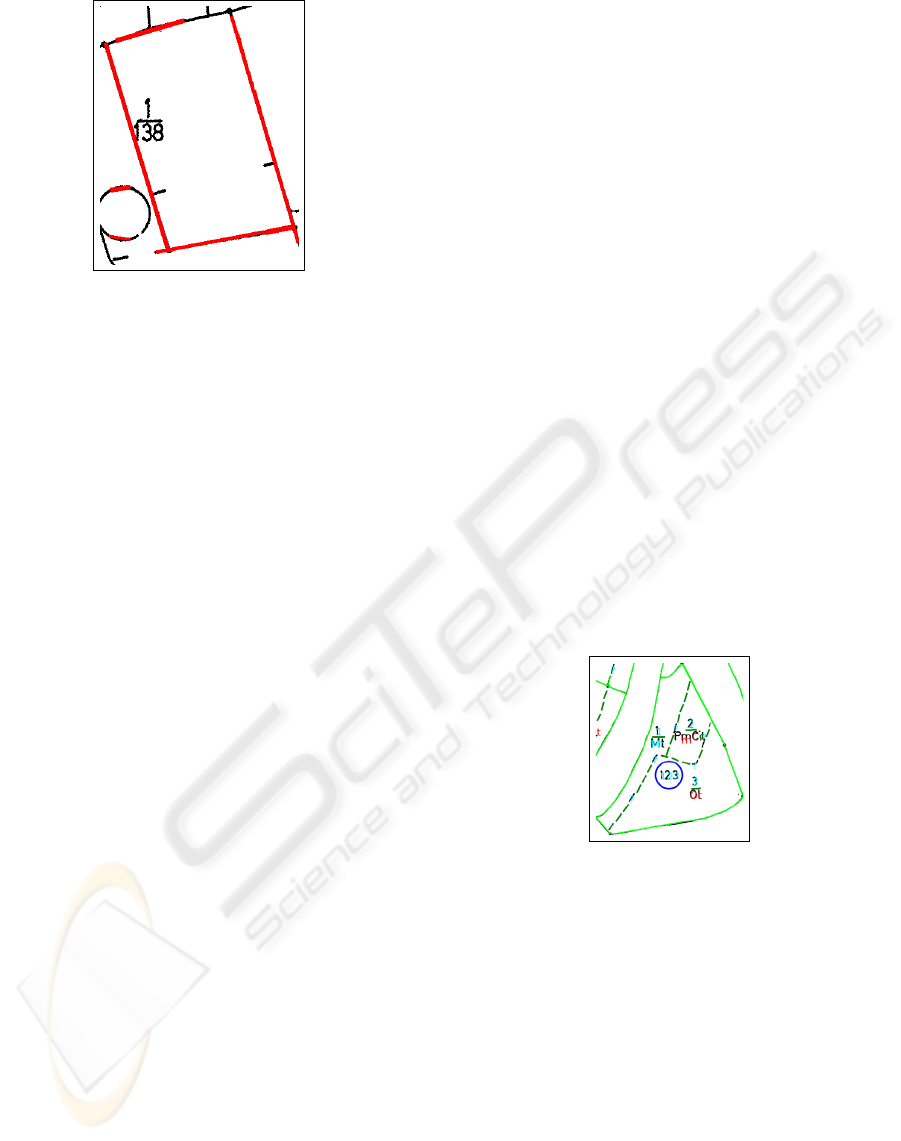
Figure 4: Segmentation of the characters and the dashes

from the contour.

tect some straight lines of the contour and segment the

elements from the contour. Finally, having the plain

contour we can apply the block ﬁll algorithm again to

extract the contour points.

3.4 Rosin-West Algorithm

The contour extraction is implemented using the

block ﬁll algorithm. After of the contour points are

obtained they are veriﬁed to assess if the contour has

big discontinuities or if the list of contour points is

too small. The Lohmann’s algorithm is used in the

ﬁrst case while the seed segment algorithm is used in

the second one. After of the identiﬁcation of the al-

gorithm to use, a window over the map is used with

center in the circle position. This is important to lo-

cally process each parcel since the two methods are

slow and the ﬁrst one needs to calculate the distance

transform image and we do not need it to all the map.

After the application of the previous algorithms, it

is necessary to vectorize the contour. The contour

points are drew in an image and vectorized using the

Rosin-West algorithm (Rosin and West, 1989). At

the end of this process, the segments are obtained and

they can be post-processed by the next algorithm.

3.5 Segment Following Algorithm

The contour segments obtained from the vectoriza-

tion can have symbols or dashes connected on contour

and discontinuities. The dashes connected on contour

can be found considering that three segments have a

common point, the segment that represent the dash is

smaller than a threshold value and its orientation is

the most different of the three collinear segments.

If the contour has a discontinuity that is smaller

than a threshold value then we can close the contour

adding the necessary segment. This can be very useful

for small discontinuities since it happens frequently.

The problem of the symbols connected is more dif-

ﬁcult to solve, it can be detected since there is a se-

quence of small continuous segments with different

orientations (there is not a stable sequence of orienta-

tions). These small segments were removed and the

contour is veriﬁed to see if it has only small disconti-

nuities by removing the segments, otherwise this is a

problematic situation. The dashes and symbols con-

nected to the contour are added to the list of the par-

cel’s objects.

At the end, if the contour is closed and every seg-

ments are used to follow the contour then the contour

is valid.

4 RESULTS AND DISCUSSION

We developed our algorithms using a set of 5 cadas-

tral maps with A0 size and digitalised, a map has in

average 10 000x8 000 pixels. A map is a huge sheet

and has a great quantity of information, so we can see

a huge diversity of shapes, symbols, characters and

contours in a single map. In each one, there are prob-

lems for the contour extraction but we have veriﬁed

that all of these drawbacks are contained in the cases

studied by the three algorithms. We consider the 5

cadastral maps studied representative of the diversity

of the Portuguese cadastral maps.

Figure 5: Example of a large contour without problems in

the extraction.

Our sheets have many types of contours but in most

cases they are large contours and there are not any el-

ements connected to the contour (see ﬁgure 5). The

gaps on contour frequently happen but these discon-

tinuities are small and the block ﬁll algorithm is suf-

ﬁcient to handle the problem. The big gaps are less

frequent since they are originated by two close dis-

continuities, and this is solved by the Lohmann’s al-

gorithm. The problem of the open contours with small

and big discontinuities are completely solved since

these contours are obtained without many problems.

In most cases the dashes connected on contour are

detected and this problem is considered solved too.

However, some dashes connected on contour are also

connected to characters and that difﬁcults consider-

AUTOMATIC EXTRACTION OF CLOSED CONTOURS IN THE PORTUGUESE CADASTRAL MAPS

431

ably the problem. Thus, the simpler cases are solved

while the difﬁcult problems are very speciﬁc and we

do not consider their solution yet, since we are look-

ing for general algorithms at this level of recognition.

The problem of the characters connected on con-

tour is a more difﬁcult problem. The seed segment al-

gorithm detects the straight lines but it does not detect

all the straight lines on the contour, so if a character is

connected on a curve or on a straight line that was not

detected, then the character is not erased. The contour

in ﬁgure 6 is composed by straight lines and in this

case is possible to segment the characters from the

contour. The contour post-process do not remove all

the characters connected on contour, since the method

previously described only remove the cases where the

character only has one segment collinear with the con-

tour. In the ﬁgures 7 and 8 we can see some difﬁcult

problems of the contour extraction since in the ﬁrst

case there is more than one segment collinear between

the contour and the character and in the second case

is the same situation and the element in on a curve. In

the other cases the problem is more difﬁcult to detect

and we do not consider it yet. As this problem hap-

pens less than 5% in each map, we think that it is not

too problematic and do not inﬂuence considerably the

results.

Figure 6: Example of a thinned contour with some elements

connected.

The implementation of the algorithms were made

in different levels of abstraction. We started consid-

ering few contours and at the end we considered the

results of all the contours in 5 maps. The tunning of

the algorithms and the identiﬁcation of all the prob-

lems is very important to improve the system. Since

the contour is extracted at a low level, so it is impor-

tant to consider only the main drawbacks and distinct

the particular from the general problems, avoiding in-

troduce more complexity into the main goal.

The results of the contour extraction are considered

good since the recognition rate is higher than 70% in

each map. Furthermore, the process of contour ex-

traction is fast, spending only 2 minutes on an Intel

Pentium IV at 3.0MHz, in average for each sheet.

The general classiﬁcation of the system is good and

we consider that it is already a valid prototype, since

the system complexity level and the recognition rate is

balanced. We think that the ideas and concepts devel-

Figure 7: Example of characters connected to the contour.

oped are correct and the next steps should be the opti-

mization of the algorithms and the resolution of some

difﬁcult problems. The algorithms works well in dif-

ferent types of maps namely urban or rural cadastral

maps.

Figure 8: Example of characters connected to a curved con-

tour.

5 CONCLUSIONS

Once the problems are complex and very different in

each map, the analysis should be made with simple

methods. The approach should be general and not

particular, so one method should solve only one prob-

lem. Because it is not possible to extract all the con-

tours from the maps, we should design the algorithms

to extract most of them. Thus, ﬁrst the problems need

to be completely identiﬁed to choose the algorithms

features and to obtain a higher recognition rate.

The results are good and the system can extract

more that 70% of the contours in each maps. The

algorithms studied are sufﬁcient to solve all the prob-

lems of the contour extraction of the Portuguese

cadastral maps. The recognition rate could be im-

proved solving particular problems but doing this

we will increase the system complexity and the im-

provement of the results are not a true consequence

again. This happens because the system should be

balanced between its complexity and the recognition

rate. Using the methods presented here we can con-

clude that the problem of the contour extraction is

globally solved.

ACKNOWLEDGEMENTS

This work was partially funded by the FCT (Fundac¸

para a Ci

encia e Tecnologia), project ACID, contract

SRI/34257/99-00 - Automatic Cadastral Information

Digitalization.

VISAPP 2006 - IMAGE ANALYSIS

432

REFERENCES

di Baja, G. (1994). Well-shaped, stable and reversible

skeletons from the (3,4)-distance transform. Journal

of Visual Communication and Image Representation,

5(1):107–115.

Dori, D. and Wenyin, L. (1999). Sparse pixel vectorization:

An algorithm and its performance evaluation. IEEE

Trans. on PAMI, 21(3):202–215.

Dosch, P., Tombre, K., Ah-Soon, C., and Masini, G. (2000).

A complete system for analysis of architectural draw-

ings. International Journal on Document Analysis and

Recognition, pages 102–116.

Jean-Marc Viglino, M. P.-D. (2003). A vector approach for

automatic interpretation of the french cadatral map. In

ICDAR, pages 304–308.

Jiqiang Song, F. Su, H. L. and Cai, S. (2002a). Raster to

vector conversion of construction engineering draw-

ings. Automation in Construction, 11(5):597–605.

Jiqiang Song, M. Cai, M. L. and Cai, S. (2002c). A new ap-

proach for line recognition in large-size images using

hough transform. In Proc. IAPR International Confer-

ence on Pattern Recognition (ICPR02),Quebec City,

Canada, August 11-15, pages I:33–36.

Jiqiang Song, M. Cai, M. L. and Cai, S. (August 11-15

2002b). Graphics recognition from binary images:

One step or two steps. In Proc. IAPR International

Conference on Pattern Recognition (ICPR02), Quebec

City, Canada.

Kass, M., Witkin, A., and Terzopoulos, D. (1987). Snakes:

Active contour models. In Proc. of IEEE Conference

on Computer Vision, pages 259–268, London, Eng-

land.

Lohman, G. (1995). Computer Analysis of images and Pat-

terns, chapter A new method of extracting closed con-

tours using maximal discs. Lecture Notes in Computer

Science 970, Springer-Verlag. V. Hlavac and R. Sara.

Rosin, P. L. and West, G. A. (1989). Segmentation of edges

into lines and arcs. Image and Vision Computing, 7(2),

pages 109-114.

Shahbazkia, H. (1998). Reconnaissance invariante et ac-

quisition de connaissance: application au traitement

automatique des plans de cadastre franc¸ais. PhD the-

sis, Universit

e Louis Pasteur de Strasbourg.

Song, J., Su, F., Tai, C., and Cai, S. (2002). An object-

oriented progressive-simpliﬁcation based vectoriza-

tion system for engineering drawings: Model, algo-

rithm and performance. IEEE Transaction on Pattern

Analysis and Machine Intelligence, 24(8):1048–1060.

Song, J., Su, F., Tai, C., Chen, J., and Cai, S. (Jun. 2000).

Line net global vectorization: an algorithm and its

performance evaluation. In Proc. IEEE International

Conference on Computer Vision and Pattern Recogni-

tion (CVPR?00), South Carolina, U.S.A., pages 383–

388.

Spinello, S. and Guitton, P. (2004). Contour line recognition

from scanned topographic maps. In WSCG (Winter

School of Computer Graphics).

Tombre, K., Ah-Soon, C., Dosch, P., Habed, A., and Masini,

G. (1998). Stable, Robust and Off-the-Shelf Meth-

ods for Graphics Recognition. in Proceedings of the

14th International Conference on Pattern Recogni-

tion, Brisbane (Australia), pages 406–408.

Tombre, K., Ah-Soon, C., et al. (september 1999). Sta-

ble and robust vectorization: How to make the right

choices. Proceedings of Third IAPR International

Workshop on Graphics Recognition (Jaipur, India),

pages 3-16.

Tombre, K. and Tabbone, S. (september 2000). Vectoriza-

tion in graphics recognition: To thin or not to thin.

Proceedings of 15th International Conference on Pat-

tern Recognition, Barcelona (Spain), 2, pages 91-96.

AUTOMATIC EXTRACTION OF CLOSED CONTOURS IN THE PORTUGUESE CADASTRAL MAPS

433