A FAST ALGORITHM FOR N D POLYHEDRAL SCENE

PERCEPTION FROM A SINGLE 2D LINE DRAWING

Hongbo Li

Key Laboratory of Mathematics Mechanization

Chinese Academy of Sciences, Beijing 100080, China

Lei Huang

Key Laboratory of Mathematics Mechanization

Chinese Academy of Sciences, Beijing 100080, China

Keywords:

nD Perception, Polyhedral Scene, Structural Cognition, 2D Line Drawing, Face Identiﬁcation.

Abstract:

In this paper, we study the problem of reconstructing the polyhedral structures of a general nD polyhedral

scene from its single 2D line drawing. With the idea of local construction and propagation, we propose a

number of powerfultechniques for general face identiﬁcation. Our reconstruction algorithm, called “nDView”,

is tested by all the 3D examples we found in the literature, plus a number of 4D and 5D examples we devised.

Our algorithm does not prerequire the dimension n of the object nor the dimension m of its surrounding space

be given, and allows the object to be a non-manifold in which neighboring faces can be coplanar. Another

striking feature is its efﬁciency: our algorithm can handle 3D solids of over 10,000 faces, with a speed 100

times as fast as the fastest existing algorithms on 2D polyhedral manifold reconstruction.

1 INTRODUCTION

Representing and perceiving an nD object has been

a very fascinating problem in both science and art

(Miyazaki, 1983). For n = 3, the simplest represen-

tation is a line drawing which is the 2D projection of

the wireframe of the object, like drafting in geometric

design and mathematical diagram. To perceive an nD

object one needs to rebuild the nD structure from its

2D projection.

How can the n dimensions be recovered from a rep-

resentation in which almost all dimensions are lost?

To start with, let us analyze how a solid in 3D space

is perceived. No one can direct his eyesight to pierce

through the solid. The only perceived object is the

boundary of the solid, which is a 2D closed manifold.

It is the closedness that allows us to ﬁll the bound-

ary with solid content to achieve one more dimension.

When we watch a line drawing of the wireframe of a

solid, which is essentially one dimensional, we ex-

tract each cycle of edges, either ﬁll it by a plane or by

some other surface to improve its dimension by one.

Then we detect if any closed manifold is formed by

the planes and surfaces, and if so, gain one more di-

mension by ﬁlling the closed manifold with solid con-

tent. The closedness of a manifold and a pattern to ﬁll

it are the two essential things in our 3D perception

from low dimensional data. The following concept

generalizes this observation to nD object perception.

The wireframe model of an nD object consists of

(1) a set of edges connecting a ﬁnite set of points,

called vertices of the object, (2) a subset of rD cycles

for 0 < r < n, called boundary rD cycles, which are

the boundaries of the (r+1)D pieces of the object, (3)

a set of ﬁlling patterns, each for a boundary rD cycle.

The simplest ﬁllings are afﬁne ﬂats. The correspond-

ing wireframe models are called polyhedral scenes.

They can be used to approximate other shapes and

thus are among the most thoroughly studied models.

In this paper we consider only such models.

A transparent line drawing of a wireframe model

is the image of a perspective or parallel projection

from the surrounding mD afﬁne space of the wire-

frame model to the image plane, such that all the

edges and vertices are revealed, and if three vertices

are not collinear in the mD space, nor should their

images.

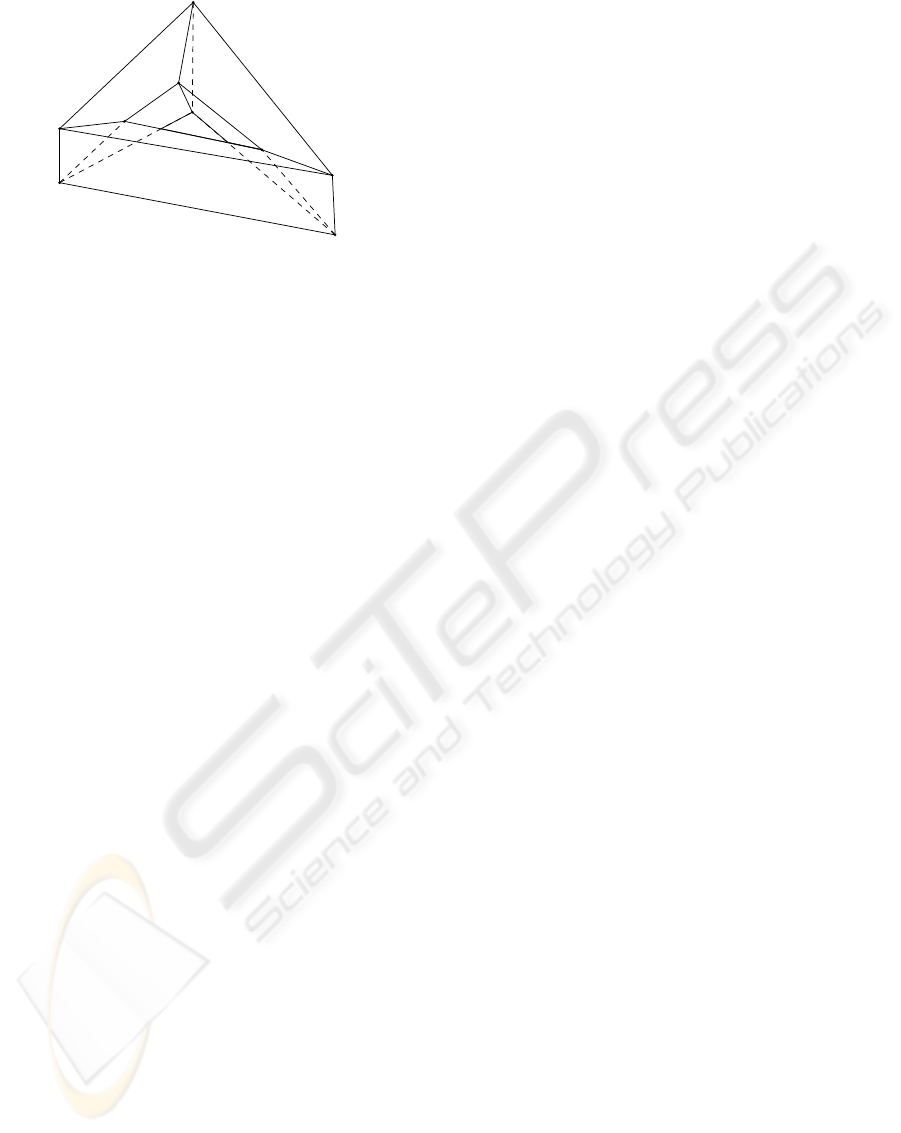
Figure 1 shows a (transparent) line drawing of a

torus in 3D space. It has 6 triangular cycles and 9

square cycles of edges. If all the 15 cycles of edges

are interpreted as polyhedral faces, then the 2D faces

form 6 cycles of faces which are the boundaries of 6

triangular columns. If the 6 cycles of faces are inter-

preted as triangular columns then they form a cycle of

3D faces, which is the boundary of a 4D ball, i.e., the

cycle of 3D faces forms a 3D sphere. So if the object

Li H. and Huang L. (2006).

A FAST ALGORITHM FOR N D POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 69-76

DOI: 10.5220/0001363100690076

 SciTePress

F3"

F2"

F1"

F1’

F3’

F2’

V2"

V3"

V1’

V2’

V3’

V1"

Figure 1: A torus in 3D space.

is required to be a 3D manifold, then the line draw-

ing has a unique interpretation which is a 3D sphere.

On the other hand, if the object is required to be a 2D

manifold, then the line drawing has another unique in-

terpretation, which is a torus in which the 6 triangular

cycles are hollow instead of being ﬁlled.

This example shows that the problem of wireframe

reconstruction from a single line drawing is rather

“ill-posed”: without a priori knowledge on the shape

and dimension, any cycle can be either ﬁlled up or

hollow, and the result is always a solution. What is

the criterion for a “most plausible solution”?

There are three cases each with its own criterion.

The ﬁrst case is on a single 2D manifold in 3D space

(Liu et al., 2002). Most applications, e.g., the drafting

of machine parts, belong to this case. The criterion

is that all given vertices and edges must be included

in a 2D manifold such that the neighborhood of every

vertex and edge is homeomorphic to a disc. The sec-

ond case is on objects in 3D world in which no two

neighboring faces are coplanar. The criterion for an

optimal solution is that it should be most likely iden-

tiﬁed by a human being. Quantitatively this criterion

is described as follows (Shpitalni and Lipson, 1996):

There should be as many faces as possible passing

through as many edges as possible. The third case is

the most general one: we consider polyhedral scenes

of maximal dimension n in an mD surrounding space

in which neither m nor n is given, the objects need

not be a single manifold and two neighboring faces

can be coplanar. In Section 2 of this paper, a principle

of psychological selection is proposed as the criterion

for optimal solution in this case.

For several decades, the study of wireframe models

and their reconstructions has been an active research

topic in computer-aided design, computer graphics

and computer vision (Agarwel and Waggenspack,

1992), (Ganter and Uicker, 1983), (Courter and

Brewer, 1986), (Hanrahan, 1982), (Marill, 1991). In

the literature, all algorithms for 3D reconstruction

consist of two steps: searching for all the cycles in the

wireframe which are face candidates, and then iden-

tifying faces from the candidates. Each step has ex-

ponential complexity, so the reconstruction from 2D

to 3D has double exponential complexity. Since the

problem is NP-complete theoretically, most research

focuses on improving the practical efﬁciency by re-

ducing the number of potential faces produced in the

ﬁrst step, i.e., in cycle searching. However, all the al-

gorithms in the literature are global in that the search-

ing is within the whole wireframe. A consequence

is that the number of potential faces is usually much

larger than the number of real faces. There remains a

lot of room for further improvement in efﬁciency.

In this paper, we ﬁrst extend the study of polyhe-

dral scene reconstruction from 3D to nD, under the

most general assumption that neither the dimension

n of the object nor the dimension m of its surround-

ing space is given, and whether or not the object is a

manifold is unknown. We then propose several pow-

erful new techniques for face identiﬁcation, and de-

sign an algorithm for fast and general face identiﬁca-

tion. Among the new techniques, the most prominent

one is localization, i.e., the cycle searching and face

identiﬁcation are carried out locally and the results are

propagated locally. In the classical case m = n = 3,

our algorithm can handle complicated 3D objects of

over 10,000 faces, outperforming all other algorithms

in both speed and range of application. For the exam-

ples in (Liu and Lee, 2001), (Liu et al., 2002), (Sh-

pitalni and Lipson, 1996), our algorithm can generate

all the solutions for ambiguous wireframes, and pro-

duces much fewer redundant cycles which are not real

faces.

The study of general nD scene reconstruction from

a single line drawing is valuable at least in scien-

tiﬁc visualization and high-dimensional animation in

entertainment industry: scientists and artists may be

very much excited to ﬁnd that their conceptual and

spiritual nD object be readily embodied in, perceiv-

able and recognizable from a single 2D line drawing.

2 N D POLYHEDRAL SCENE

COGNITION

2.1 Constraints on Line Drawings

A perspective projection from mD to 2D is the com-

position of m − 2 successive perspective projec-

tions whose projective centers are linearly indepen-

dent vectors, and at least one center is an afﬁne point.

A parallel projection from mD to 2D is the compo-

sition of m − 2 successive parallel projections whose

projective centers are linearly independent directions.

A naive way of visualizing such a projection is to

imagine watching a TV program, in which there is

VISAPP 2006 - IMAGE UNDERSTANDING

a guy watching another TV program, and in that TV

program there is still another guy watching still an-

other TV program, etc. If each TV program is ob-

tained by a pinhole camera through perspective pro-

jection, then the m − 2 successive perspective projec-

tions transforms the mD world into a 2D image.

The reconstruction is the inverse procedure of the

above sequence of projections: the input is the 0D

and 1D information displayed in a 2D space: vertices

and edges of the polyhedral scene; the reconstruction

from 2D to 3D is to identify the real 2D faces of the

scene; going this way, the reconstruction from (m −

1)D to mD is to identify the real (m − 1)D faces.

In a wireframe model, a 0D face is a vertex, a 0D

cycle is the two vertices of an edge, and a 1D face is an

edge. For r > 0, an rD cycle is a set of rD faces such

that (1) if two faces intersect, the intersection belongs

to their iD faces for 0 ≤ i < r, (2) any (r − 1)D face

of one rD face is shared by exactly one other rD face

in the set. For r > 1, an rD face is an (r − 1)D cycle

ﬁlled by the rD afﬁne ﬂat surrounded by it.

If two rD faces share at least two (r − 1)D faces

which are in different (r − 1)D planes, then the two

rD faces must be in the same rD afﬁne plane, i.e.,

coplanar. The union of a set of rD coplanar faces

is called an rD polyface, and the faces are said to be

merged together. An advantage of this concept is that

usually we do not need to decompose a polyface into

non-overlapping faces.

Some geometric constraints must be satisﬁed for

an (r − 1)D cycle to be eligible for being an rD face.

In previous work on face identiﬁcation, it is gener-

ally assumed that any two neighboring faces are not

coplanar. We feel that this is too strong a constraint to

include many interesting models, so we discard it.

Figure 2: Face adjacency constraint (left: if both ACDEB

and F CDEG are 2D faces then they must be coplanar);

Non-self-intersection constraint (right: since edges HI and

J K intersect not at a vertex, cycle H I JK cannot be the

projection of a 2D face).

The polyhedral setting imposes a strong constraint,

called the rD face adjacency constraint (Shpitalni and

Lipson, 1996): if two rD faces share two (r − 1)D

faces which are in different (r − 1)D afﬁne planes,

then the two rD faces must be in the same rD afﬁne

plane, i.e., are coplanar.

In a line drawing of an mD polyhedral scene, if two

edges are collinear, so are they in the mD scene; if

two edges cross not at a vertex, they do not intersect

in the mD scene. By a perspective projection, a 2D

face is projected onto a 2D region of the image plane

whose boundary does not intersect itself. The 2D non-

self-intersection constraint says that if two edges in-

tersect not at a vertex, then they cannot belong to the

same 1D cycle.

The 2D non-interior-intersection constraint (Liu

et al., 2002) says that if two 1D cycles intersect at

only two vertices and the line segment between the

two vertices intersects both the enclosed regions of

the 1D cycles in the image plane, then either the two

cycles form a polyface, i.e., are coplanar, or at most

one can be assigned as a face.

Figure 3: Non-interior-intersection constraint (left: If both

ABC DE and H GC F E are 2D faces then they must be

coplanar, otherwise their intersection CE must be a visible

edge); Chordless constraint (right: cycle IJ LM K contains

a chord J K, so it is not assigned as a face, instead, I JK

and J LM K can be assigned as faces).

If an rD face F does not belong to an rD cycle C

but its intersection with C is exactly the boundary of

F , then F is called a chord of C. A face with chord

can always be decomposed along its chord into two

coplanar faces, and can thus be replaced by the two

faces sharing the chord. However, the two faces need

not be coplanar any more. To gain more degree of

freedom in the reconstruction, an rD cycle with chord

is not assigned as a face. This is the rD chordless

constraint.

2.2 Principle of Psychological

Selection

For a general object in an unknown environment, a

human tends to choose a face identiﬁcation in which

there are as many edges as possible participating in

as many faces as possible, which is the guideline for

the algorithms in (Liu and Lee, 2001) and (Shpitalni

and Lipson, 1996). If the dimension is unknown, the

most important goal should be to ﬁnd the highest di-

mension n, for which the above guideline may not be

helpful.

Our principle of psychological selection is that for

r > 1, the rD face identiﬁcation should make as

many (r − 1)D faces as possible participating in as

many rD faces as possible, such that the sequence of

A FAST ALGORITHM FOR ND POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING

numbers of non-coplanar iD faces is maximal lexico-

graphically, for i from n down to r.

For example, if a line drawing has two explana-

tions, one is two 3D faces together with ﬁfty 2D faces

not belonging to the 3D faces, the other is one 3D face

together with one hundred 2D faces not belonging to

the 3D face, such that any two faces of the same di-

mension are not coplanar, then it is the former expla-

nation that is chosen as the optimal solution. Thus,

our principle of psychological selection is different

from that in (Liu and Lee, 2001) and (Shpitalni and

Lipson, 1996). Its goal is to ﬁnd ﬁrst the highest di-

mension n, second as many as possible nD faces that

are non-coplanar.

2.3 Principle of Rigidity

To improve the speed for ﬁnding the ﬁrst optimal so-

lution, it is very important to arrange the face can-

didates in such an order that the most plausible ones

come ﬁrst. We classify the cycles according to their

rigidity so that they have different levels of priority in

face identiﬁcation.

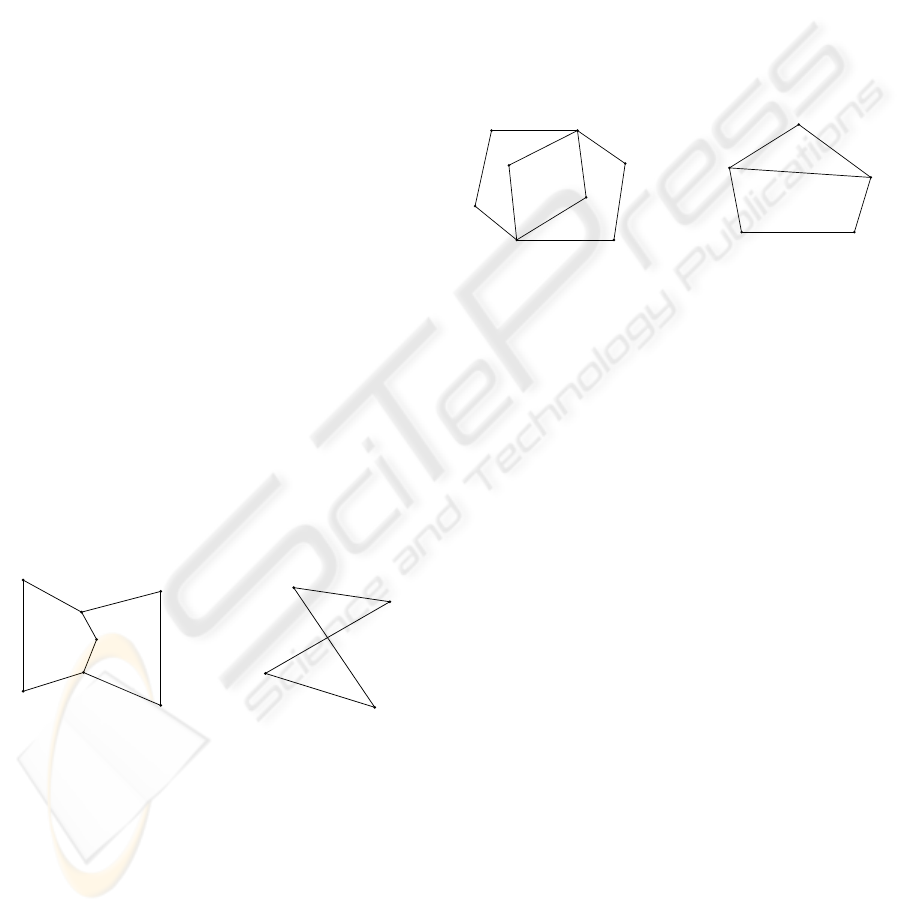
By the deﬁnition of a cycle, the supporting afﬁne

plane of an (r − 1)D cycle has dimension at least r.

If in the geometric reconstruction from rD to (r +

1)D, for a given (r −1)D cycle in the rD afﬁne plane,

the dimension of the conﬁguration space of the lifted

cycle is k + r + 1, then the rigidity of the cycle is

deﬁned to be −k, and the ﬂexibility of the cycle is

deﬁned to be k. A cycle of rigidity 0, or −1, or < −1

is said to be rigid, or elastic, or plastic respectively.

For example, if r = 2, a 1D cycle of k + 3 non-

collinear vertices has rigidity −k, see Figure 4. How-

ever, most rigid cycles are not boundaries of sim-

plices. For example, the boundary of any column or

wedge is a 2D rigid cycle.

E F

J K

Figure 4: Rigidity of 1D cycles: rigid (left), elastic (middle)

and plastic (right).

Our principle of rigidity is that rigid cycles are al-

ways identiﬁed as faces, and elastic cycles are more

likely to be faces than plastic ones. The explanation

is as follows:

1. Rigid cycles are boundaries of either real or interior

faces of the object. If they are all assigned as faces,

they never force any two faces of different planes

to be coplanar. If the object is not assumed to be a

manifold, then taking all rigid cycles as real faces

conforms to the principle of psychological selec-

tion.

If the object is required to be a manifold, then tak-

ing all rigid cycles as real faces induce a decompo-

sition of the object into smaller ones of the same di-

mension, and by our manifold assembly algorithm

to be introduced in the next section, all interior

faces can be removed.

2. Elastic cycles are next to rigid ones in simplicity.

Experiments show that they are the next most plau-

sible face candidates.

3 NEW TECHNIQUES AND

ALGORITHM FOR

COGNITION

Below we propose several new techniques for struc-

tural reconstruction based on the above perception

principles. Without loss of generality, we only de-

scribe the classical case of ﬁnding 1D cycles in 2D

face identiﬁcation.

3.1 Localization

To speed up the ﬁnding of the highest dimension, we

propose to search for the cycles locally in the wire-

frame, then propagate the result to construct more cy-

cles. This technique proves to be effective also in re-

ducing the number of redundant cycles.

Let C be a wireframe model. A local wireframe

model of C is a subset of the vertices of C together

with all the higher dimensional faces formed by the

subset of vertices. A localization ﬁlter, or localiza-

tion, of C is a sequence of local wireframe models

⊂ S

⊂ . . . ⊂ S

= C in which each successor

introduces more vertices than its predecessor. With

the introduction of new vertices, all the edges among

them and the existing vertices are introduced.

Localization is often realized by propagation

through edges. Starting from a vertex called the ori-

gin, we localize the wireframe by considering only

the subgraph of the origin and its neighboring ver-

tices. Within the local wireframe we identify the

faces. Then we set the origin to be the current local

wireframe, and repeat the localization and identiﬁca-

tion procedure. By introducing new vertices accord-

ing to the closeness of their relations with the existing

ones and the rigidity of the cycles formed by them,

the complexity of cycle searching can be reduced.

In Figure 5(a), a localization goes as follows:

{1} ⊂ {1, 2, 3, 4} ⊂ {1, 2, 3, 4, 5, 6, 7, 8, 9, 0}

⊂ {1, 2, 3, 4, 5, 6, 7, 8, 9, 0, a, b, c}.

VISAPP 2006 - IMAGE UNDERSTANDING

b 7

(a)

b 7

(b)

Figure 5: Localization, deletion and blocking.

3.2 Deletion

To further control the number of face candidates,

we propose two techniques deletion and blocking, to

reduce the scope of cycle searching by deleting or

blocking the branches that do not produce any new

face candidates.

For a general object, the criterion for an edge to be

deletable is that the deletion does not inﬂuence the ﬁ-

nal identiﬁcation of 2D faces and polyfaces. By our

principle of psychological selection, an edge E in the

procedure of localization can be deleted if by assign-

ing any new cycle through it as a face, (1) the num-

ber of non-coplanar faces does not increase, (2) if any

new vertex V is to be added into the polyface con-

taining the face, there is always a cycle of edges in

the polyface that passes through V but not E, i.e.,

deleting E does not prevent V from joining the poly-

face via a cycle of edges. The following theorem can

be proved within graph theory.

Deletion Theorem. In cycle searching, if for an

edge E not collinear with any other edge, all its

neighboring edges are already in faces containing

edge E, then E can be deleted. Such an edge is said

to be saturated.

In Figure 5(a), if three cycles 125a04, 138c94

and 126b73 are already assigned as faces, then edges

12, 13, 14 are saturated and can be deleted. Then ver-

tex 1 is no longer connected to any other vertex and

can be deleted. See Figure 5(b).

3.3 Path Blocking

In Figure 5(b), the vertices in the localization form

a big cycle 25a049c837b6. This cycle cannot be a

face, otherwise all three constructed faces have to

be merged. In searching for more face candidates

passing through a ﬁxed vertex, those faces having

been identiﬁed can block off some search branches

by avoiding identiﬁed faces to merge, according to

our principle of psychological selection. This tech-

nique is extremely useful in reducing the number of

branches in cycle searching.

For a general object, if a branch of edges intersects

a face at least at three vertices which are not collinear,

then the branch is blocked by the face. The block is

called a face block. If a branch meets two different

face blocks, then it is blocked permanently. If along a

branch there is only one face block, then the branch of

edges can be merged with the face to form a polyface.

In Figure 5(b), suppose we want to ﬁnd a new cy-

cle passing through vertex 2. From 2 to 6, the path

is blocked by face 62137b. From 2 to 5, the path

is blocked by face 04125a. The two different face

blocks permanently block any new cycle from pass-

ing through branch 625.

In (Liu et al., 2002), the models are 2D manifolds in

which no two neighboring faces are coplanar. If a cy-

cle is identiﬁed as a face then no other branch passing

through two edges of it can generate a face. Here one

face sufﬁces to block off the branch permanently. For

a general object, this single blocking does not work.

There are other types of blocks. The 2D non-self-

intersection constraint can block some branches per-

manently. The blocks are called intersection blocks.

The 2D non-interior-intersection constraint can block

some branches from including the interior of an exist-

ing face. The blocks are called interior blocks. The

2D chordless constraint can permanently block some

branches from generating cycles with chords. The

blocks are called chord blocks.

3.4 Manifold Assembly

In many applications it is required that the object be a

2D manifold. For this special purpose, there are two

alternatives to revise our general-purposed structural

reconstruction algorithm:

Anterior Approach: Employ the a priori constraints

of a 2D manifold in the general algorithm from

the start, by revising the localization, deletion and

blocking techniques accordingly (Liu et al., 2002).

Posterior Approach: Use the general algorithm to

produce a set of 3D faces which are themselves 2D

manifolds. Assemble the 3D faces into a single 2D

manifold. This approach, called manifold assem-

bly, appears to be more efﬁcient than the previous

one.

Our manifold assembly algorithm follows a local

propagation approach, and employs the following 2D

manifold assembly principles:

Principle 1. (Face assembly) If two 3D faces inter-

sect at a 2D face whose edges are of degree greater

than two, then the 3D faces can be assembled at the

2D face by removing it; if one edge has degree two,

then one 3D face must be deleted.

Remark: For a set of rD faces, the degree of an

(r − 1)D face with respect to the set is the number

A FAST ALGORITHM FOR ND POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING

(a)

(b)

Figure 6: Manifold assembly principles.

of elements in the set passing through the (r − 1)D

face.

For example, in Figure 1 we can assemble columns

′

′′

and F

′′

, and denote the result by

O. Then face F

′′

is deleted, and its neighbors

, F

′

, F

′′

, F

′′

each have a degree-2 edge. The

four neighbors disallow the other four columns to be

annexed to O. As a result, vertex V

′′

is absent from

O. Although O itself is a 2D manifold, it does not

provide the whole line drawing with such an explana-

tion.

Principle 2. (Edge assembly) If two 3D faces inter-

sect at an edge E but not at any 2D face, then they

can be assembled at the edge if and only if within

the line drawing, a 2D face F

at E in one 3D face

is within the 2D region of a 2D face F

at E in

the other 3D face. If no such two 2D faces then

one 3D face must be deleted; else the assembling

is realized by replacing the two 2D faces by their

difference in the polyface generated by them.

For example, in Figure 6(b) cube ABCDEF GH

and tetrahedron IJ KL share a common edge IJ.

Face IJK can be merged into either face BCEG or

face ABGH. On the other hand, face IJL can only

be merged into face BCEG. As a result, face IJK

can only be merged into face ABGH.

Principle 3. (Vertex assembly) If two 3D faces in-

tersect at a vertex V but not at any 2D face or edge,

then they can be assembled at the vertex if and only

if within the line drawing, a 2D face F

at V in

one 3D face is within the 2D region of a 2D face

at V in the other 3D face. If no such two 2D

faces then one 3D face must be deleted; else the

assembling is realized by replacing the pair of 2D

faces by their difference in the polyface generated

by them.

For example, in Figure 6(a) cube 12345678 and

tetrahedron 3abc intersect at vertex 3. Face 2376 can

be merged with either face 3ab, or face 3ac, or face

3bc, leading to three different manifold structures.

Principle 4. (Empty assembly) If two 3D faces do

not intersect, then they can be assembled at two 2D

faces if and only if one 2D face is within the 2D

region of the other 2D face. To assemble the two

3D faces is to replace the pair of 2D faces by their

difference in the polyface generated by them.

For example, in Figure 6(a) cube 12345678 and

cube ABCDEF GH can be assembled at either the

pair of faces (1234, ABCD), or the pair of faces

(1584, ABCD), leading to two different manifolds.

Principle 5. (Orientation assembly) If two 3D

faces are assembled then their orientations must be

compatible at their common 2D faces.

For example, in Figure 6(b) cube ABCDEF GH

and column NOP QRS can be assembled in four dif-

ferent ways:

(1) (ABCD, N OP ) and (EF GH, QRS),

(2) (ADF H, NOP ) and (EF GH, QRS),

(3) (ABCD, N OP ) and (BCEG, QRS),

(4) (ADF H, NOP ) and (BCEG, QRS).

In assemblings (2) and (3) the orientations of the

cube and the column are incompatible at their com-

mon faces, so only assemblings (1) and (4) are al-

lowed.

3.5 The Main Algorithm – nDView

Input: (1) a 2D line drawing composed of vertices

and edges. A vertex is represented by its 2D coor-

dinates, an edge by two vertices.

(2) A set of lines. A line is represented by a se-

quence of collinear edges.

(3) A vertex as the origin of localization.

Output: Objects of dimension > 1: faces and poly-

faces.

Initialization: Find all pairs of edges intersecting not

at a vertex.

Step 1. Localization start: Start from the origin,

use localization to generate a set of new vertices.

Step 2. Cycle searching: Generate faces by the

depth-ﬁrst cycle searching strategy, together with

the deletion and blocking techniques.

Step 3. Dimension upgrading: Start from the 2D

local wireframe constructed so far, construct higher

dimensional faces in a hierarchical order, following

a procedure similar to Steps 1 to 3.

Step 4. Assembling: It occurs if the result is re-

quired to be a manifold of given dimension. The

assembling is also local.

Step 5. Localization end: Go back to Step 1 for an-

other round of localization. Terminate after all ver-

tices are included.

Step 6. More solutions and completeness: Explore

the state-space trees to get more (or all) solutions.

The vertices of the rD state-space tree are rD

VISAPP 2006 - IMAGE UNDERSTANDING

non-rigid cycles with their states. A vertex here

has two states: either the cycle is identiﬁed as a

face, or not allowed to be a face. A descendent

of a vertex in the tree is a cycle found after the

vertex (cycle with a state) has been found in the

localization.

Remark. (1) Although a speciﬁc set of 2D co-

ordinates are given in the input, they are used

only to test the inequalities occurring in the 2D

non-self-intersection constraint, the 2D non-interior-

intersection constraint and the 3D assembly. A solu-

tion based on these coordinates is acceptable as long

as the polyhedral structures are compatible, no matter

if the coordinates satisfy the realizability conditions

for nD geometric reconstruction. This is true for all

face identiﬁcation algorithms in the literature.

(2) The main algorithm above improves the practi-

cal efﬁciency but not the theoretical one. Step 6 is a

procedure having double exponential complexity for

a ﬁxed dimension r. For the examples tested in our

experiments, the algorithm can always ﬁnd a solution

reaching the maximal dimension without resorting to

Step 6. if a different solution is needed, then chang-

ing the origin of localization in the imput is usually a

better option than carrying out Step 6.

3.6 Experiments

We have implemented nDView in VC++ 6.0,

have tested all the examples in (Agarwel and

Waggenspack, 1992), (Liu and Lee, 2001), (Liu et al.,

2002), (Shpitalni and Lipson, 1996), etc., in addition

to a dozen higher dimensional ones designed by our-

selves, e.g. the line drawings in Figure 7.

(a)

(b)

(c)

4 7

(d)

Figure 7: 4D cube (a); 5D polytope (b); 4D polytope (c);

5D polytope (d).

For the classical case m = n = 3, we make com-

parison between our algorithm and the existing fastest

algorithm for face identiﬁcation of 2D manifolds (Liu

et al., 2002), using the steam box model shown in

Figure 8(a) and a sequence of N steam boxes con-

nected by cubes as typical 2D manifolds of genus N.

The reason for this choice is that Figure 8(a) is the

most complicated example in (Liu et al., 2002) and

about half of the cycles constructed there are redun-

dant ones, in sharp contrast to all other examples in

that paper.

a b

(a)

(b)

Figure 8: Face identiﬁcation.

The following table collects some data from our ex-

periment. In the table, by “global search” we mean

the algorithm in (Liu et al., 2002), by “local search”

we mean our algorithm nDView. The table reveals

that for very small N our algorithm runs a little bit

slower, but very soon with the growth of N, our algo-

rithm runs much faster. For n = 100 our algorithm

runs more than 100 times faster than the algorithm in

(Liu et al., 2002). Figure 9 in the next page shows the

comparison of the computing time graphically. The

tests are made on an HP Desktop PC of Intel 3.40GHz

CPU and 1GB RAM.

N Global search Local search G : L

time G (sec.) time L (sec.)

1 0.006 0.025 0.24

10 6.172 1.890 3.26

20 23.796 7.094 3.35

30 189.589 16.687 11.36

40 450.031 31.687 14.20

50 1165.547 53.077 21.96

60 1745.013 81.578 21.39

70 2383.511 118.328 20.14

80 4513.983 165.358 27.29

90 16148.985 230.562 70.04

100 41327.325 320.765 128.83

A FAST ALGORITHM FOR ND POLYHEDRAL SCENE PERCEPTION FROM A SINGLE 2D LINE DRAWING

4 CONCLUSION

In this paper, we study the problem of machine per-

ception of nD polyhedral scenes from a single 2D line

drawing. We propose a number of efﬁcient techniques

for the structural reconstruction. By testing them with

classical 3D examples, we ﬁnd their superiority over

existing ones. The work should prove to be valuable

for high-dimensional scientiﬁc and artistic visualiza-

tions.

N: number of steam boxes

10080

time

(minutes)

Local Search

Global Search

N: number of steam boxes

100806040200

time

(minutes)

500

300

400

200

100

Local Search

Global Search

Figure 9: Comparison of computing time: local search

(solid line) vs global search (dashed line).

REFERENCES

Agarwel, S. and Waggenspack, C. (1992). Decomposition

method for extracting face topologies from wireframe

models. In Computer Aided Design. 24(3): 123–140.

Courter, S. and Brewer, J. (1986). Automated conversion

of curvilinear wireframe models to surface boundary

models. In Comput. Graph. 20(4): 171–178.

Ganter, M. and Uicker, J. (1983). From wireframe to solid

geometric: Automated conversion of data representa-

tions. In Computer in Mechanical Eng. 2(2): 40–45.

Hanrahan, P. (1982). Creating volume models from edge-

vertex graphs. In Computer Graphics. 16(3): 77–84.

Liu, J. and Lee, Y. (2001). A graph-based method for face

identiﬁcation from a single 2d line drawing. In IEEE

Trans. on PAMI. 23(10): 1106–1119.

Liu, J., Lee, Y., and Cham, C. (2002). Identifying faces in

a 2d line drawing representing a manifold object. In

IEEE Trans. on PAMI. 24(12): 1579–1593.

Marill, T. (1991). Emulation the human interpretation of

line drawings as 3d objects. In International J. of

Computer Vision. 6(2): 147–161.

Miyazaki, K. (1983). An Adventure in Multidimensional

Space: The Art and Geometry of Polygons, Polyhedra,

and Polytopes. Wileyinterscience Publ.

Shpitalni, M. and Lipson, H. (1996). Identiﬁcation of faces

in a 2d line drawing projection of a wireframe object.

In IEEE Trans. on PAMI. 18(10): 1000–1012.

VISAPP 2006 - IMAGE UNDERSTANDING