LOCAL KERNEL COLOR HISTOGRAMS FOR BACKGROUND

SUBTRACTION

Philippe Noriega, Benedicte Bascle, Olivier Bernier

France Telecom, Recherche & Developpement

2, av. Pierre Marzin, 22300 Lannion, France

Keywords:

Histograms, background subtraction, color quantization.

Abstract:

In addition to being invariant to image rotation and translation, histograms have the advantage of being easy

to compute. These advantages make histograms very popular in computer vision. However, without data

quantization to reduce size, histograms are generally not suitable for realtime applications. Moreover, they

are sensitive to quantization errors and lack any spatial information. This paper presents a way to keep the

advantages of histograms avoiding their inherent drawbacks using local kernel histograms. This approach is

tested for background subtraction using indoor and outdoor sequences.

1 INTRODUCTION

A normalized color histogram is easy to compute

and is invariant to rotation and translation of im-

age content. It is robust regarding partial occlusions

of objects of interest in the scene. These advan-

tages explain why histograms are widely used in com-

puter vision. Examples of applications are: content

based image retrieval (CBIR) (Han and Ma, 2002;

Pass and Zabih, 1996; H. Yamamoto and Takemura,

1999), tracking (B. Han and Davis, 2005; M. Ma-

son, 2001), background subtraction (A. Elgammal

and Davis, 2000; K. Toyama and Meyers, 1999)...

However, histograms have some drawbacks. First,

they lack any spatial information: two images can

have the same histogram and be dissimilar due to a

different ordering of the pixels in the images. A sec-

ond drawback occurs when histogrammed data is in-

sufﬁciently quantized. This problem generally im-

plies large histograms (several thousands of bins) re-

quiring important computation costs and preventing

real-time computation. Histograms are also sensi-

tive to image noise and to quantization errors that

may cause bin changes even though image variation

is small. So, bin by bin comparison measure can lead

to important dissimilarities between histograms from

similar pictures.

The goal of local kernel histograms is to deal with

these drawbacks while keeping the advantages of his-

tograms. This technique is applied on background

subtraction using local kernel color histograms to

demonstrate its efﬁciency. The next section presents

the related works, section 3 describes the local ker-

nel histograms taking example on color feature ex-

traction, section 4 explains how to apply them to

background subtraction, experimental results are pre-

sented in section 5 and section 6 concludes this paper.

2 RELATED WORKS

Some histogram techniques permit to recover miss-

ing spatial information. The color cooccurrence his-

togram (Chang and Krumm, 1999; Huang et al.,

1997) is an elegant solution where a histogram bin

b is associated with two colors c

, c

and a distance

d. The histogram bin b(c

, c

, d) records the number

of (c

, c

) colored pixel pairs wich are d distant. A

variant consist in only considering pixels belonging

to contours (Crandall and Luo, 2004). Color cooc-

currence histograms tend to have a huge number of

bins making real time computation difﬁcult. Another

solution is to split the histogram bins in two classes

to classify coherent and incoherent pixels of the same

color (Pass and Zabih, 1996). A pixel is considered as

coherent if it is part of a homogeneously colored zone.

Otherwise, the pixel is considered as incoherent. This

method needs clustering algorithms to deﬁne the ho-

mogeneous zones. A last solution for this problem

consists in dividing the image in regions and comput-

213

Noriega P., Bascle B. and Bernier O. (2006).

LOCAL KERNEL COLOR HISTOGRAMS FOR BACKGROUND SUBTRACTION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 213-219

DOI: 10.5220/0001363302130219

 SciTePress

ing a histogram for each one. Each histogram is asso-

ciated with a local zone in the image providing spatial

information. A variant consists in dividing the im-

age in equal squares and compute one histogram for

each square (M. Mason, 2001). The Multi-Scale His-

togram Intersection Representation (MSHIR) (Gargi

and Kasturi, 1999) is another variant. It is a global to

local representation where the image is divided into

decreasing scale blocks. Another similar approach

consists in recursively dividing the image into regions

until each region has a homogeneous feature distribu-

tion or until the size of each region becomes smaller

than a given threshold value (H. Yamamoto and Take-

mura, 1999).

To reach real-time performance, it is necessary to

reduce the amount of data by quantizing the fea-

ture space before histogram computation. Consider-

ing color histograms, quantization consists in putting

close colors in the same histogram bin. Quantization

can be performed in different color spaces. (M. Ma-

son, 2001) applies a color depth reduction formula

to transform the 24-bit RGB color space to 12-bit,

(Crandall and Luo, 2004) work in CIE LAB color

space and reduce it to 267 standard colors in a ﬁrst

stage before keeping only 10 basic colors. The CIE

LAB space has the advantage of being perceptually

uniform i.e. the Euclidean distance between two

colors corresponds to the human perception differ-

ence. The calculation of the distance between two

histograms is another way to reach real time com-

putation. In the case of quadratic histogram distance

(J. L. Hafner and Niblack, 1995), the weight matrix

that contains the coefﬁcients denoting the similarity

between histogram bins can be diagonalized ofﬂine.

Filling several histogram bins with a unique pixel

is a good method to reduce inﬂuence of noise and

of quantization errors in histogram computation (Han

and Ma, 2002). Quadratic distance (J. L. Hafner and

Niblack, 1995) yields the same advantage but use

only the Euclidean distance in histogram similarity

computation.

3 COLOR LOCAL KERNEL

HISTOGRAMS

In the proposed technique, image is segmented into

overlapped local squares with a histogram for each

one to provide accurate spatial information. To re-

duce signiﬁcantly the amount of data without loosing

important information because of coarse quantization,

the color space is quantized according to the most rep-

resentative colors extracted from the scene. A double

Gaussian kernel, one in the image space and one in

the color space bring robustness against noise. Tech-

nical implementation is described further below.

3.1 Image Partitioning

Histograms must be computed from a group of pix-

els. For maximum spatial accuracy, the image is par-

titioned in n × n square like regions that are over-

lapped with the same gap g for both image axis co-

ordinates. So, excluding the image edges, a pixel be-

longs to N

= (n/g)

regions.

On one hand, n must be large enough to smooth

both camera vibrations and waving objects in the

scene. On the other hand, too large regions prevent

accurate objects of interest detection. In experimental

results, n is ﬁxed at 12 pixels with a gap g = 3. More

overlapping requires excessive computing resources.

3.2 Color Quantization

Quantization allows saving computer resources by re-

ducing the histogram sizes. Because camera noise

prevents distinguishing between all the 256×256 col-

ors in the U V space, this last is reduced to 40 × 40

colors. Then, a good option is quantizing taking into

account the most representative colors in the scene.

In this way, n

colors are selected from the image

reference to be associated to n

histogram bins. An

undeﬁned color bin is added for other unselected col-

ors. Thus, all pixels not corresponding to one of the

selected colors is associated with the undeﬁned color

bin.

This approach brings a great improvement in term

of computation time. To represent more than ninety

percent of reduced colors in a cluttered scene, the

color histogram size is set to only 15 color bins.

Moreover, this size is smaller than those reached

by good quantization: 64 with fuzzy histograms in

CBIR application (Han and Ma, 2002) or 1600 bins in

CIELAB (Crandall and Luo, 2004), and much smaller

than those usually reached: 4096 for the tracking al-

gorithm presented in (M. Mason, 2001) or 9796 for

color cooccurrence histograms (Chang and Krumm,

1999).

3.3 Kernels

Instead of associating one pixel with a unique region

and a unique histogram bin, Gaussian kernels are in-

troduced in both image and color space to bring more

ﬂexible fuzzy associations between image and his-

tograms. Gaussian kernels are also chosen because of

its smoothing properties and are easily computed. For

computation efﬁciency, the kernels are pre-computed

and stored in lookup tables.

3.3.1 Spatial Gaussian Kernel

Pixels S

, y

) in a local area l are weighted in

terms of distance from the area center. Thus, to com-

VISAPP 2006 - IMAGE ANALYSIS

214

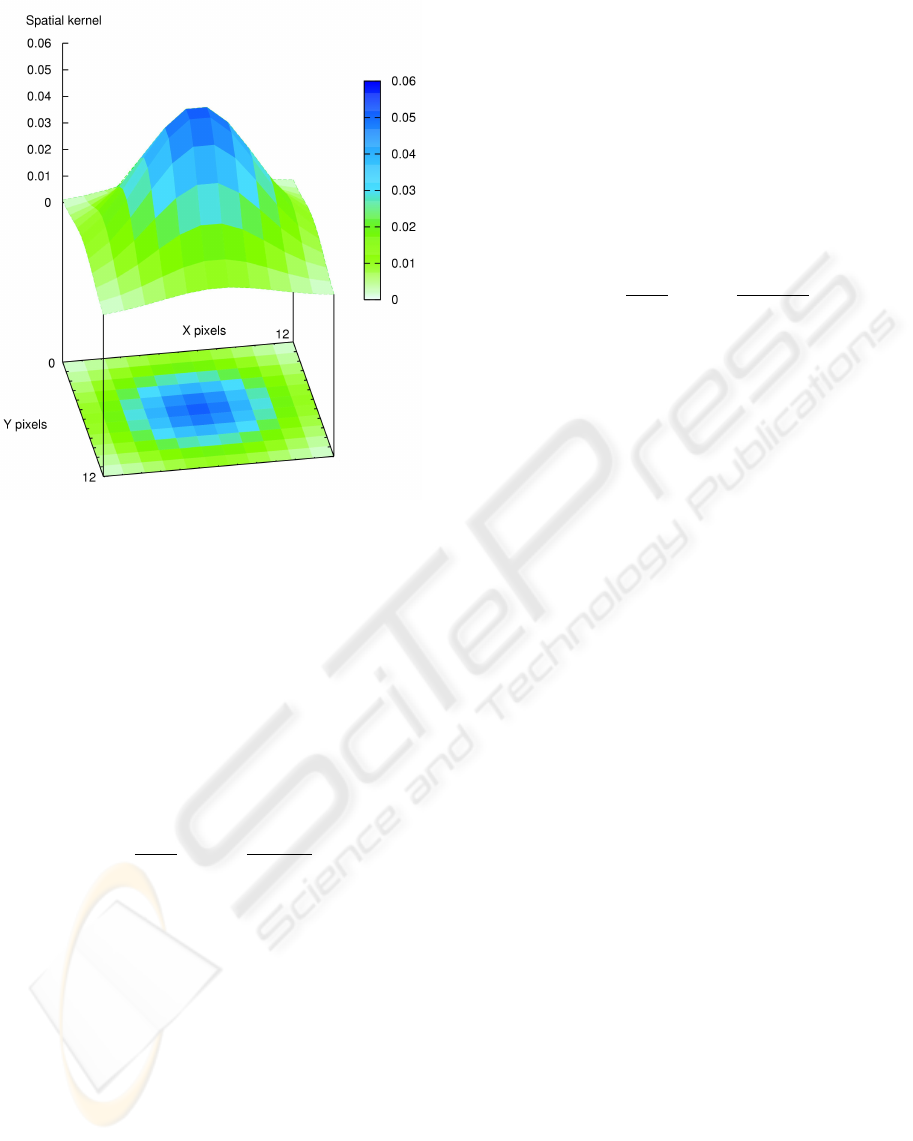
Figure 1: Spatial Gaussian kernel on a local area of 12 × 12

pixels. The standard deviation is low enough (σ

= 3) to

provide good smoothing properties.

pute the local histogram H

, the pixel contributions

are weighted according to a bi-dimensional spatial

Gaussian kernel G

(µ

, σ

) with mean µ

, y

) on

the area center and standard deviation σ

(see Figure

1). K

is a normalization coefﬁcient:

= x

− x

= y

− y

) =

2πσ

exp

−

+ d

2σ

(1)

The ratio weight between the border and center

area of regions must be low enough to provide good

smoothing properties. Thus, the standard deviation

is chosen to be about a quarter of the local area

size. This setting brings 95 percent of the Gaussian

kernel inside the area and gives a ratio weight of

about 0.135. K

normalizes the kernel on the area:

k=1

) = 1.

3.3.2 Color Gaussian Kernel

Two different colors falling in two separate histogram

bins are considered dissimilar even if they are very

close. This is a signiﬁcant classical histogram draw-

back.

Using a color Gaussian kernel alleviates this prob-

lem and takes into account colors similarity. In-

stead of falling into a unique histogram bin, a

pixel is shared between several bins according to

a Gaussian weight G

. In Y UV color space and

given h

, a bin representing the color (U

, V

) in the

chrominance histogram, the contribution of the pixel

, y

, Y

, U

, V

) to the h

bin is:

= U

− U

= V

− V

, V

) =

2πσ

exp



−

+ d

2σ



(2)

is a normalization coefﬁcient determined for

the color (U

, V

) among the n

colors in the reduced

space:

i=1

, V

) = 1. Standard deviation σ

is estimated by taking into account the camera noise.

3.4 Local Kernel Histograms

Computation

As explained above, local kernel histograms are com-

puted from image overlapped regions taking into ac-

count the two Gaussian kernels: the former in image

space and the second in color space.

In a local area l, the value of a h

histogram bin

corresponding to a selected color (1 ≤ j ≤ n

) is:

k=1

) . (3)

For the undeﬁned color bin, all occurs as if his-

togram contains all the n

colors in the reduced space

(1 ≤ j ≤ n

). Then, the value of the undeﬁned color

bin is the sum of unselected color bins:

j+1

(j=n

+1)

. (4)

Of course, for fast histogram computation, contri-

butions of each colors in the reduced color space are

pre-computed in lookups tables. The normalized his-

togram H

contains n

colors bins plus the undeﬁned

color bin. It is normalized due to the normalization

constants K

and K

4 APPLICATION TO

BACKGROUND SUBTRACTION

In background subtraction, histograms are often used

to extract spatial or temporal features of background.

LOCAL KERNEL COLOR HISTOGRAMS FOR BACKGROUND SUBTRACTION

215

Those can being color or contours orientation for spa-

tial features or pixel value versus frame number in

the case of temporal features. For example (A. El-

gammal and Davis, 2000) compute their background

model using histograms that describe temporal statis-

tics for pixels values. In their region scale process,

(K. Toyama and Meyers, 1999) use histograms to

compare moving regions between frames. This sec-

tion describes how to apply local kernel histograms in

color background subtraction to obtain a pixel scale

probability map.

4.1 Local Area Probability

As histograms are normalized, the Bhattacharyya dis-

tance between them provides a result between 0 and

1 which can be assimilated as a probability. Given

histograms H

and H

computed from the same

area l respectively in reference and current image,

the probability P

that l belongs to the background

is computed applying Bhattacharyya distance to the

histogram bins h

j=1

. (5)

4.2 Pixel Probability

Area histogram similarity computation provide an

identical probability for all the pixels in the area.

Thus, the resulting probability map is heavily aliased.

If it is suitable for tracking (M. Mason, 2001), back-

ground subtraction needs generally more spatial ac-

curacy. Overlapping between areas reduce aliasing

but there is a trade off between computation time and

gap size between areas. To provide a pixel scale map

while preserving computation ressources, the prob-

ability is computed with the probabilities resulting

from the N

areas that a pixel belongs to. Taking ac-

count of the spatial kernel G

, the probability P

for

the pixel S(x

, y

, Y

, U

, V

) is:

l=1

. (6)

5 EXPERIMENTAL RESULTS

The local kernel histograms are compared with three

other algorithms in the ﬁeld of background subtrac-

tion. Each algorithm use chrominance channels U V

from Y UV color space:

Mean & Threshold: Pixel-wise mean values

are computed during a training phase, and pixels

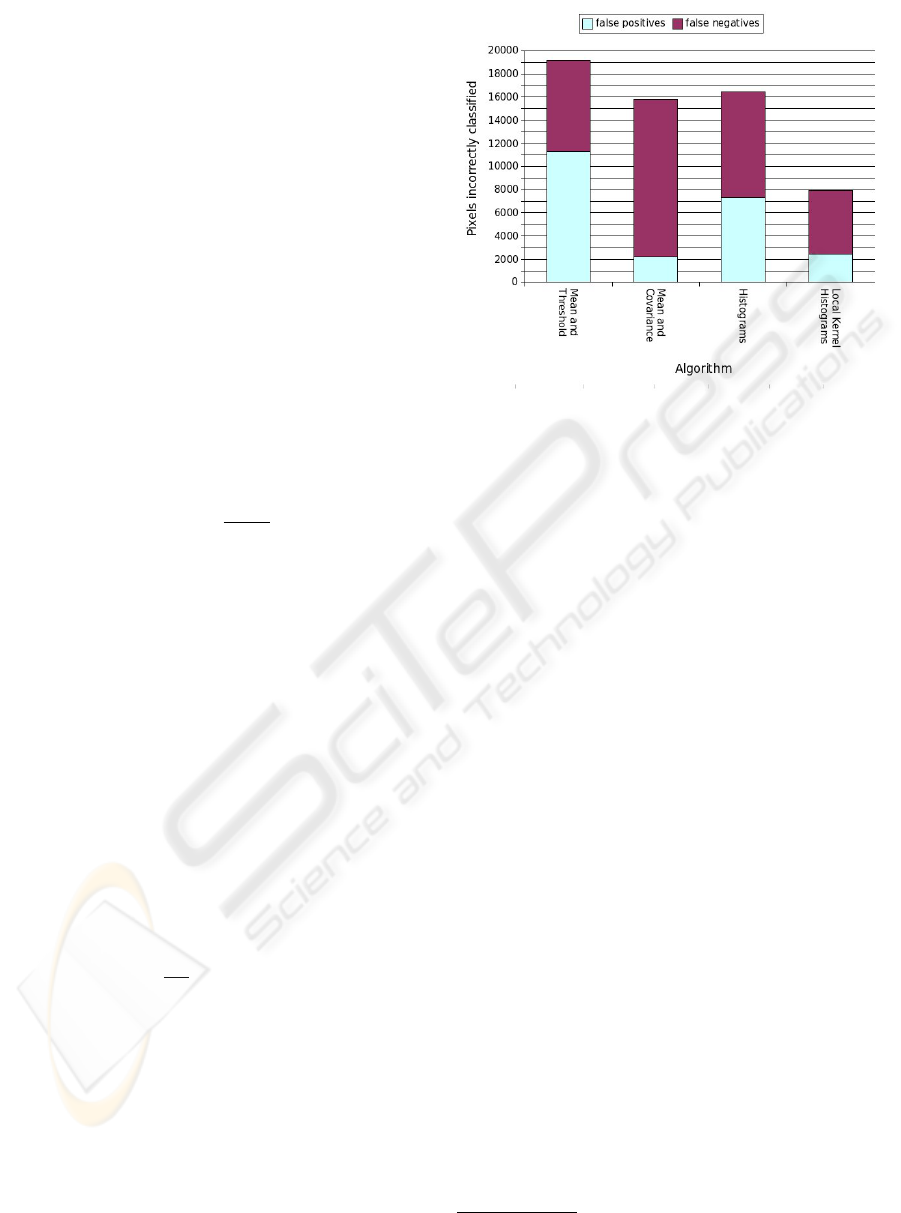
Figure 2: Algorithms overall performance.

within a ﬁxed threshold of the mean are considered

background.

Mean & Covariance: The mean and covari-

ance are computed from the recent samples values

for pixels. Foreground pixels are determined using a

threshold. This is similar to the background algorithm

used in (A. Elgammal and Davis, 2000).

Histograms: Frames are segmented into 50%

large overlapped square zones of 20 pixels. A

conventional color histogram is computed from

each zone for both reference and current image.

Similarity is computed with histogram intersection

and a threshold determines foreground pixels: see

(M. Mason, 2001).

Local Kernel Histograms: The method explained in

this paper, probability map is thresholded to extract

silhouettes.

Both indoor and outdoor test sequences are used

(see Figure 3). The third (foreground covers monitor

pattern) and the fourth (waving trees) sequences were

used by (K. Toyama and Meyers, 1999). They are

available from the web

in color with a 160×120

pixels resolution. The ﬁrst indoor scene was grabbed

with a color CCD camera using 384×288 pixels

resolution and the last outdoor scene with a webcam

and a 320×240 pixels resolution. Image quality is

relatively poor. The ﬁve sequences show classical

difﬁculties for background subtraction:

http://research.microsoft.com/users/jckrumm/

WallFlower/TestImages.htm

VISAPP 2006 - IMAGE ANALYSIS

216

Table 1: Performance of algorithms on various images test.

Problem Type and his Associated Frame Test

Camera Indoor Foreground Waving Unexpected

Vibrations Covers Trees Gust of

Error Monitor Wind Total

Algorithm Type (frame 235) (frame 235) (frame 251) (frame 247) (frame 246) Errors

Mean and false neg. 0 6351 457 104 971

Threshold false pos. 2787 1848 195 1905 4554 19172

Mean and false neg. 0 6788 3273 977 2589

Covariance false pos. 49 603 89 116 1333 15817

Histograms false neg. 0 4525 2455 931 1207

false pos. 338 4507 32 96 2359 16450

Local Kernel false neg. 0 3247 664 195 1390

Histograms false pos. 0 692 146 495 1126 7955

Camera Vibrations: Camera is not strongly

ﬁxed and vibrations cause small image motion.

Shadows and Reﬂections: A person stays be-

tween the window and the door. Shadow and

reﬂections slightly modify the background on the left

side of the picture.

Foreground Covers Monitor Pattern: A mon-

itor lies on a desk with rolling interference bars. A

person walks into the scene and occludes the monitor.

Waving trees: A person walks in front a sway-

ing tree.

Gust of Wind: A person walks in front of swaying

ﬂowers. Suddenly, a gust of wind occurs. The ﬂowers

move with more intensity.

The test images are shown in Figure 3. Tests are

performed on a single frame from each sequence and

consist in segmenting a human subject from the back-

ground. Mean & Threshold and Mean & Covariance

algorithms are both initialized during the ﬁrst 200

frames before the test. Histogram based algorithms

are only trained with the ﬁrst image of the test se-

quence.

Because histograms naturally have the capacity to

smooth noise, camera vibrations and swaying ﬂowers

do not affect histogram based algorithms. If the Mean

and Covariance algorithm succeeds on the waving

trees scene, it needs a certain time to adapt its back-

ground model causing false detections when an unex-

pected event occurs e.g. a gust of wind. On the other

hand, conventional histograms fail when shadows and

reﬂections appear in the scene. In this case, U V

colors channels are slightly modiﬁed yielding pixels

jumps between histograms bins and obviously, con-

ventional histograms bin by bin comparison measures

fails. It is a classical histogram drawback. However,

small color changes do not affect local kernel his-

tograms because the color kernel reduces quantization

errors. Conventional histograms (M. Mason, 2001)

result in strongly aliased foreground detection. Thus,

because of their poor spatial accuracy, histograms are

generally not suitable for silhouette pose or gesture

analysis. However, local kernel histograms provide

spatial accurate probability maps (cf. § 4) for silhou-

ette extraction.

The results of the tests are shown in Figure 2 and

table 1. As in (K. Toyama and Meyers, 1999), per-

formances are evaluated in term of number of fore-

ground pixels marked as background (false negatives)

and background pixels marked as foreground (false

positives). Ground truth is provided by hand seg-

mentation. It is obvious that the few test sequences

produced in this paper are not sufﬁcient to correctly

evaluate the difference between the algorithms. How-

ever, results underline the capacity of local kernel

histograms to naturally smooth noise from camera,

soften shadows or reﬂections and waving background

objects.

In terms of computation load, the local kernel his-

tograms modelizes a local area including n

pixels

with a histogram comprising n

+1 bins. In our exper-

iments, 144 pixel in a local area are modelized with

only 16 bins. Moreover, Gaussian kernels are pre-

computed and stored in lookup tables, yielding a fast

histogram computation. Thus, even with strong over-

lapping between local areas, computation times are

close to those required by the Mean & Threshold al-

gorithm.

6 CONCLUSION

As shown in experimental results, the local kernel

histogram based algorithm is a robust and efﬁcient

LOCAL KERNEL COLOR HISTOGRAMS FOR BACKGROUND SUBTRACTION

217

method to extract color information from images.

Even in noisy environment with camera vibrations

or swaying vegetation, they provide useful and accu-

rate probability map for background subtraction. This

method is easily generalizable to other features e.g.

contours, and can be useful in many ﬁelds of com-

puter vision e.g. content based image retrieval (CBIR)

or tracking. This paper has demonstrated that local

kernel histograms combine conventional histograms

advantages and avoid their inherent drawbacks to pro-

vide robust, fast and accurate spatial information. Il-

lumination robust background subtraction using con-

tour features and local kernel histograms will be ad-

dressed in future works.

REFERENCES

A. Elgammal, D. H. and Davis, L. S. (2000). Non-

parametric model for backg round subtraction. In Eu-

ropean Conference on Computer Vision, volume II,

pages 751-767. Springer-Verlag.

B. Han, C. Yang, R. D. and Davis, L. (2005). Bayesian

ﬁltering and integral image for visual tracking. In

Special session on Real-Time Object Tracking: Algo-

rithms and Evaluation in Workshop on Image Analysis

for Multimedia Interactive Services (WIAMIS).

Chang, P. and Krumm, J. (1999). Object recognition with

color cooccurrence histograms. In IEEE Conference

on Computer Vision and Pattern Recognition. IEEE

Computer Society.

Crandall, D. and Luo, J. (2004). Robust color object detec-

tion using spatial-color joint probability functions. In

IEEE Computer Society Conference on Computer Vi-

sion and Pattern Recognition (CVPR’04 ) - Volume 1,

pp 379-385. IEEE Computer Society.

Gargi, U. and Kasturi, R. (1999). Image database query-

ing using a multiscale localized color representation.

In IEEE Workshop on ContentBased Access of Image

and Video Libraries. IEEE Computer Society.

H. Yamamoto, H. Iwasa, N. Y. and Takemura, H. (1999).

Content-based similarity retrieval of images based

on spatial color distribution. In Int. Conf. on Im-

age Analysis and Processing (ICIAP), pp. 951-956.

Springer.

Han, J. and Ma, K. K. (2002). Fuzzy color histogram and its

use in color image retrieval. In IEEE Transactions on

Image Processing, vol. 11, no. 8, pp. 944-952. IEEE

Computer Society.

Huang, J., Kumar, S., Mitra, M., Zhu, W., and Zabih, R.

(1997). Image indexing using color correlograms. In

Proc. IEEE Comp. Soc. Conf. Comp. Vis. and Patt.

Rec., pages 762-768. IEEE Computer Society.

J. L. Hafner, H. S. Sawhney, W. E. M. F. and Niblack,

W. (1995). Efﬁcient color histogram indexing for

quadratic form distance functions. In IEEE Trans-

actions. Pattern Anal. Mach. Intell. 17(7): 729-736.

IEEE Computer Society.

K. Toyama, J. Krumm, B. B. and Meyers, B. (1999). Wall-

ﬂower: principles and practice of background mainte-

nance. In ICCV, pages 255-261. IEEE Computer So-

ciety.

M. Mason, Z. D. (2001). Using histograms to detect and

track objects in color video. In 30th AIPR Workshop.

pp. 154-159. IEEE Computer Society.

Pass, G. and Zabih, R. (1996). Histogram reﬁnement for

content-based image retrieval. In IEEE Workshop on

Applications of Computer Vision. IEEE Computer So-

ciety.

VISAPP 2006 - IMAGE ANALYSIS

218

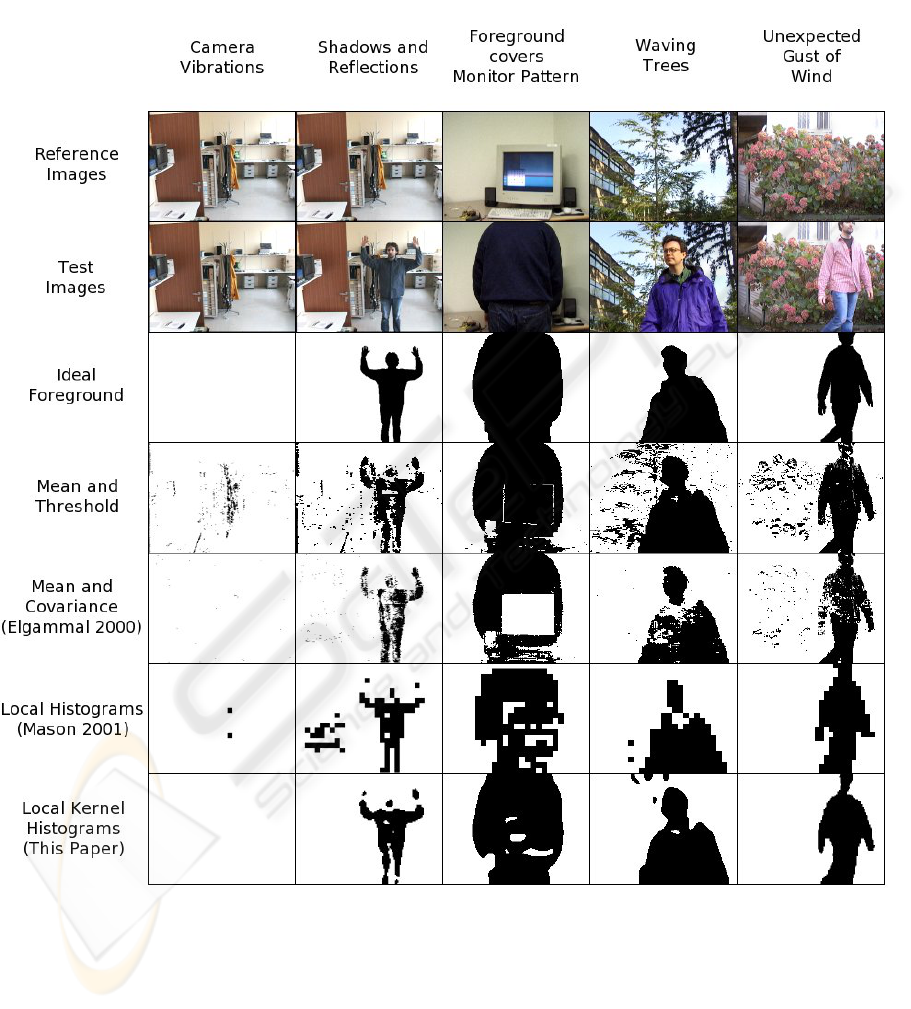
Figure 3: Comparison of color background subtraction algorithms with color local kernel histograms. The top row shows

reference images used to initialize background subtraction. The second row corresponds to original images extracted from

indoor and outdoor scenes. Third row represents hand segmented ground truth. Each other row shows the result for one

algorithm and each column represents a conventional problem.

LOCAL KERNEL COLOR HISTOGRAMS FOR BACKGROUND SUBTRACTION

219