FACIAL IMAGE FEATURE EXTRACTION USING SUPPORT

VECTOR MACHINES

H. Abrishami Moghaddam

K. N. Toosi University of Technology, P.O. Box 16315 -1355, Tehran, Iran

M. Ghayoumi

Islamic Azad University, Science and Research Unit, P.O. Box 14515-75, Tehran, Iran

Keywords: Feature extraction, Support vector machines, Face recognition, Principal component analysis, Independent

components analysis, Linear discriminant analysis.

Abstract: In this paper, we present an approach that unifies sub-space feature extraction and support vector

classification for face recognition. Linear discriminant, independent component and principal component

analyses are used for dimensionality reduction prior to introducing feature vectors to a support vector

machine. The performance of the developed methods in reducing classification error and providing better

generalization for high dimensional face recognition application is demonstrated.

1 INTRODUCTION

Choosing an appropriate set of features is critical

when designing pattern classification systems under

the frame-work of supervised learning. Ideally, we

would like to use only features having high

separability power while ignoring or paying less

attention to the rest. Recently, there has been an

increased interest in deploying feature selection in

applications such as face and gesture recognition

(Sun et al., 2004). Most efforts in the literature have

been focused mainly on developing feature

extraction methods (Jain et al., 2000,

Belhumeur, et

al., 1997) and employing powerful classifiers such

as probabilistic (Moghaddam, 2002), hidden Markov

models (HMMs) (Othman and

Aboulnasr, 2003),

neural networks (NNs) (Er et al., 2002) and support

vector machine (SVM) (Lee et al., 2002).

The main trend in feature extraction has been

representing the data in a lower dimensional space

computed through a linear or non-linear transform-

ation satisfying certain properties. Principal

component analysis (PCA) (Turk and

Pentland, 1991)

selects features which are maximally variant across

the data. With independent components analysis

(ICA) (Liu and

Wechsler, 2003) statistically

independent features result. Linear discriminant

analysis (LDA) (Yu and

Yang, 2001) encodes the

discriminatory information in a linear separable

space by maximizing the ratio of between-class to

within-class variances.

SVM have shown to be very effective classifiers

for face recognition applications and provide the

ability to generalize over imaging variants (Heisele

et al., 2001). SVM provide an optimal decision

hyperplane by employing kernel learning, projecting

the data into a high-dimensional space (Vapnik,

1995). Some authors used PCA and ICA for

dimensionality reduction before using SVM for face

recognition (Wang et al., 2002, Qi, et al., 2001).

Without using effective schemes to select an

appropriate subset of features in the computed

subspaces, these methods rely mostly on

classification algorithms to deal with the issues of

redundant and irrelevant features. This might be

problematic, especially when the number of training

examples is small compared to the number of

features. Fortuna and Capson (Fortuna and

Capson,

2004) proposed an iterative component algorithm for

feature selection by combining PCA and ICA

methods and SVM classifier.

In this paper, we present an approach that uses

SVM to classify PCA, ICA and LDA extracted

features and a hybrid iterative method for improving

the generalization of the classifier. Application of

the developed algorithm to a facial image database

480

Abrishami Moghaddam H. and Ghayoumi M. (2006).

FACIAL IMAGE FEATURE EXTRACTION USING SUPPORT VECTOR MACHINES.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 480-485

DOI: 10.5220/0001363604800485

 SciTePress

demonstrates the improvement in correctness,

margin and number of support vectors of the

classifier. The rest of the paper is organized as

follows: Section 2 provides a brief review of feature

extraction algorithms including PCA, ICA and LDA.

In section 3, we present the classification algorithm

using SVM and the iterative method for improving

the generalization of the classifier. Section 4 is

devoted to experimental results and discussion.

Finally, concluding remarks and plans for future

works are given in section 5.

2 FEATURE EXTRACTION

Given a set of centred input vectors

xxx ,...,,

n variables, a data matrix

X is defined with each

vector forming a column of

X . The goal of feature

extraction algorithms is to construct a decomposition

of the data such that a set of basis vectors for the

data which are maximally decorrelated can be found.

In other words, we look for a matrix

A such that:

XAS

(1)

where the columns of

S are decorrelated. For

pattern recognition, the decorrelated space

S is used

for dimensionality reduction.

2.1 Principal Component Analysis

Finding the principal components from

observations of

creates an nn× covariance

matrix

XXΣ = . When nN  , this is a convenient

form of the covariance matrix to use. An

covariance matrix results from

and is useful

when

Nn  . This is typically the case when an

image forms an observation and n is very large. If

the SVD is used to decompose

X as,

VUΛX

2/1

the

nn×

covariance matrix is found by:

ttt

UUΛUVΛVUΛΣ ==

2/12/1

(2)

This can be recognized as an eigen-

decomposition on

XX where U is an nn× matrix

whose columns are the eigenvectors of

XX , V is

NN × matrix whose columns are the

eigenvectors of

and Λ is an Nn× matrix

whose first

diagonal elements correspond to non-

zero eigenvalues of the covariance matrix in

descending order. Thus the

dimensional subspace

is formed by selecting the first

rows of the

transformed data matrix

X :

XUX

(3)

The

covariance matrix XX

gives:

tttt

VVΛVUΛUVΛXX ==

2/12/1

(4)

and the following relation may be used for

dimensionality reduction when

Nn  (Fortuna and

Capson, 2004):

XVX

(5)

2.2 Independent Component

Analysis

ICA is originally developed for blind source

separation whose goal is to recover mutually

independent but unknown source signals from their

linear mixture without knowing the mixing

coefficients. ICA decorrelates

X by finding a

matrix

such that

is not just decorrelated but

statistically independent. The degree of

independence is measured by the mutual information

between the components of the random variable

ss d

)(

log)()(

∏

∫

(6)

where

)(sp is the joint probability of s and )(

p s

are the marginal densities. If a nonlinear mapping

)(sy g

is applied such that

has uniform

marginal densities, it has been shown that mutual

information is obtained by (Bartlett and

Sejnowski,

1997):

yyyyy d)(log)()()( ppHI

∫

=−=

(7)

)(yI can then be minimized with:

[]

ijijij

gEg

xxAAs

)()()(log

detlog

⎥

⎦

⎤

⎢

⎣

⎡

∂

−

∑

(8)

where

[

]

denotes expected value. Multiplying

leads to the natural gradient algorithm (Shi

et al., 2004):

[

]

AxxAIA ))((

gE+∝Δ

(9)

2.3 Linear Discriminant Analysis

LDA criteria are mainly based on a family of

functions of scatter matrices. For example, the

maximization of

)(

tr ΣΣ

−

ΣΣ /

is used, where

are within and between-class scatter matrices,

respectively. In LDA, the optimum linear transform

is composed of

)( nr

≤

eigenvectors of

ΣΣ

−1

FACIAL IMAGE FEATURE EXTRACTION USING SUPPORT VECTOR MACHINES

481

corresponding to its

largest eigenvalues.

Alternatively,

ΣΣ

−1

can be used for LDA, where

represents the mixture scatter matrix

)(

wbm

=Σ

A simple analysis shows that both

ΣΣ

−1

and

ΣΣ

−1

has the same eigenvector matrix

. In general,

not full rank, hence

Σ is used in place of

. The

computation of the eigenvector matrix

from

ΣΣ

−1

is equivalent to the solution of the generalized

eigenvalue problem

Σ , where

is the

eigenvalue matrix (Fukunaga, 1990).

3 SUPPORT VECTOR

MACHINES

To perform classification with a linear SVM, a

labelled set of features

},{

yx is constructed for all

features in the training data set. The class of

feature

c is defined by }1,1{ −=

y . If the data are

assumed to be linearly separable, the SVM attempts

to find a separating hyperplane with the largest

margin. The margin is defined as the shortest

distance from the separating hyperplane to the

closest data point. If the

training data follow:

iby

∀≥−+ 01)( wx

(10)

Then the points for which the above equality

holds lie on the hyperplanes

+ b

and

1−=+ b

. The margin can be shown to be

(Cristianini and

Shawe-Taylor, 2000):

=Margin

(11)

The SVM attempts to find the pair of hyperplanes

which give the maximum margin by minimizing

subject to constraints on w . Reformulating the

problem using the Lagrangian, the expression to

optimize for a nonlinear SVM can be written as:

),(

)(

111

jijij

KyyL xx

αααα

∑∑∑

===

−=

(12)

),( xx

′

is a kernel function satisfying Mercer’s

conditions. An example kernel function is the

Gaussian radial basis function:

⎟

⎠

⎞

⎜

⎝

⎛

′

−

−=

′

exp),(

xxK

(13)

where

is the standard deviation of the kernel’s

exponential function. The decision function of the

SVM can be described by:

⎥

⎦

⎤

⎢

⎣

⎡

∑

iii

bKyf

),(sgn)( xxx

(14)

For data points which lie closest to the optimal

hyperplane the corresponding

are non-zero, and

these are called support vectors. All other

parameters

are zero. As such, any modification of

the data points which are not support vectors will

have no effect on the solution. This indicates that the

support vectors contain all the necessary information

to reconstruct the hyperplane.

3.1 General Subspace Classification

An SVM can be used to classify subspace features

(including PCA, ICA and LDA extracted features)

as described below:

i) The Transformation matrix

is determined

using the training data set

train

ii) The training and test data sets in the reduced

dimension subspace are determined as follows:

trainttrain

XAS =

testttest

XAS =

iii) Define data pairs (

train

y,s

) and apply a support

vector classifier to classify

test

3.2 Iterative Subspace Classification

In order to improve the generalization of the

classifier, an iterative algorithm which moves outlier

feature vectors toward their class mean and modifies

the basis vectors

to fit the new features has been

proposed (Fortuna and

Capson, 2004). We used this

algorithm with all three feature extraction methods

as follows:

i) find

from

train

ii) initialize:

trainttrain

XAS =

testttest

XAS =

iii) initialize the support vector coefficient matrix

to the identity matrix.

iv) repeat

v) move the support vectors toward the mean by

amount proportional to the support vector

by:

)(

meantraintraintrain

SSSS −Γ−=

vi) recalculate

by:

train

SXA

where + denotes pseudo-inverse.

vii) calculate:

trainttrain

XAS =

testttest

XAS =

VISAPP 2006 - IMAGE ANALYSIS

482

viii) define data pairs (

train

y,s ) and apply a support

vector classifier to classify

test

ix) until margin change

≺ 0.01.

4 EXPERIMENTAL RESULTS

4.1 Gaussian Mixture Data

An example of two classes, each comprising a

mixture of three Gaussian random variables, is used

to illustrate the relationship between PCA, ICA and

LDA extracted features classified by SVM. The

mixture of Gaussian data points

]

[xX = are

defined by:

})

-x()

-xexp{(

μμ

∑

})

-x()

-xexp{(

μμ

∑

where:

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=Σ=Σ=Σ===

19.

9.25.1

19.

9.25.1

19.

9.25.1

3.19

0.9

2.18

4.6

1.17

8.3

μμμ

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=Σ=Σ=Σ===

19.

9.25.1

19.

9.25.1

19.

9.25.1

9.17

0.10

7.16

0.8

6.15

0.6

μμμ

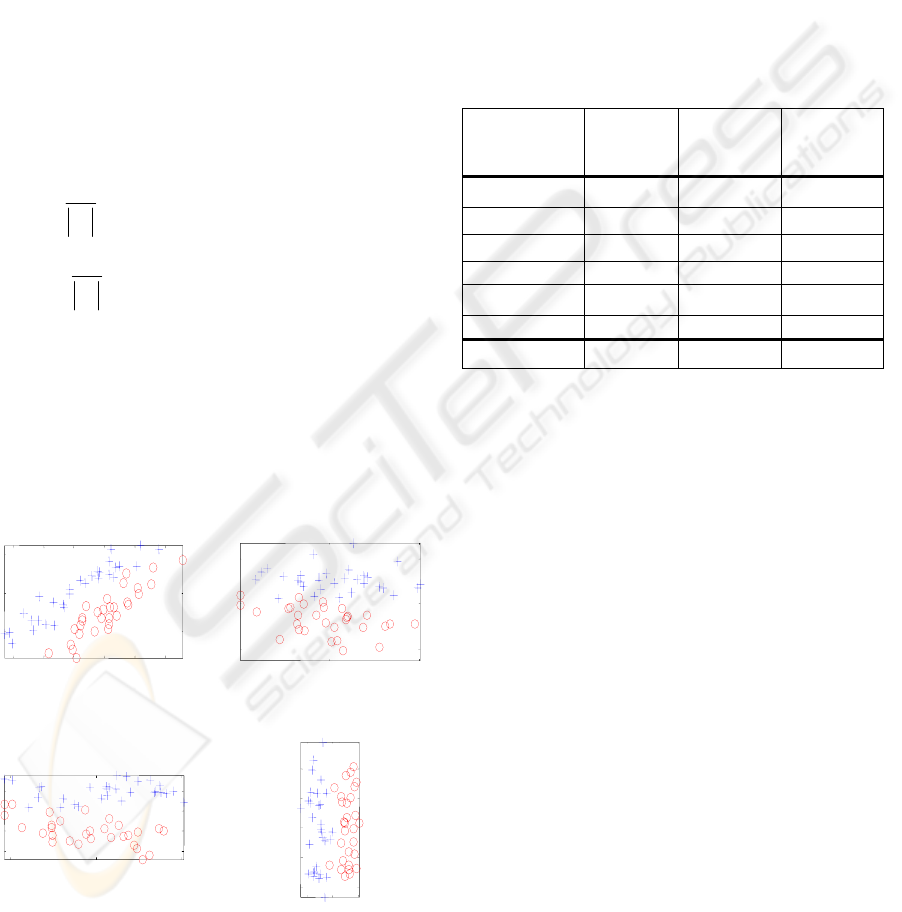
Figure 1: Example mixture of Gaussian data set: (a)

original

data, (b) principal component coefficients, (c)

independent

components coefficients, (d) Linear

discriminant coefficients.

Figure (1.a) illustrates the distribution of the original

data points in two dimensional space. Figures (1.b-d)

illustrate the transformed data by PCA, ICA and

LDA, respectively. Table (1) shows the

classification results using direct and iterative

implementation of each method. As shown, LDA

extracted features provide slightly improved

recognition performance compared to PCA and ICA

features.

Table 1: Classification results for mixture of Gaussian data

set.

4.2 Facial Image Database

The developed algorithms were also applied to Yale

face database B (Georghiades, et al., 2001). For this

experiment, 2 class recognition experiments are

performed over 36 pairs of subjects. For each pair of

subjects, a training data set is constructed from the

first 32 lighting positions for pose 1 and 2 of each

subject. The test data set comprised the same pair of

subjects imaged under the last 32 lighting position

from pose 7 and 8. The training and test images were

histogram equalized and mean centred before

subspace calculation and classification. For this

example

Nn  , so we used XX

to compute the

eigenvectors. Recognition performance (margin,

number of support vectors and error rate) was tested

for each subject pair for kernel

ranging from 1 to

5. The dimensionality of the training subspace is

reduced to 25 prior to recognition. Figures (2.a) and

(2.b) show the training images for two faces

(selected randomly) from the data set. Figs. 2(c) and

(d) show the test images for the same two faces. Fig.

3 shows the resulting principal, independent and

linear basis images for the training images shown in

Figs. 2(a) and (b). Table (2) shows the average

number of support vectors, margin and recognition

rate for the entire data set. As illustrated in Table

(2), iterative algorithms provide better generalization

Method Mean of

Margin

Mean of SV Mean of

Recognition

Rate

No subspace 0.0030 11.2720 99.4867

PCA 0.0030 11.2680 99.4800

ICA 0.0030 11.2720 99.4867

LDA 0.0029 11.0080 99.4600

PCA iterative 0.0298 7.8800 99.3397

ICA iterative 0.0260 8.1200 99.5107

LDA iterative 0.0295 6.9480 99.2941

2 4 6 8 10 12

(a)

ORGINAL

-5

0 5

-2

(b)

PCA

-5 0 5

-2

-1

(c)

ICA

-2 0 2

-4

-2

(d)

LDA

FACIAL IMAGE FEATURE EXTRACTION USING SUPPORT VECTOR MACHINES

483

of the SVM classifier. The improvement in

generalization the iterative techniques illustrated by

improved margin and reduced number of support

vectors is statistically significant for all results on

the face database.

(a) (b)

Figure 2: Example of training and test images: (a) class 1

training, (b) class 2 training, (c) class 1 test, (d) class 2

test

(a) (b)

(a) (b) (c)

(d) (e) (f)

Figure 3: Example components (contrast enhanced): (a)

images of

PCA, (b) images of ICA, (c) images of LDA,

(d)

images of iterative PCA, (e) images of iterative ICA,

(f) images of

iterative LDA.

Moreover, among three feature extraction

algorithms, LDA component representation exhibits

higher performance with respect to margin, number

of support vectors and recognition rate. In all of the

experiments, ICA consistently increased the margin

and the number of support vectors compared to raw

data and PCA component representations.

Table 2: Classification results for Yale face.

5 CONCLUDING REMARKS

In this paper, we used three feature extraction

methods including PCA, ICA and LDA to reduce the

dimensionality of the training space. An iterative

algorithm was utilized to further enhance the

generalization ability of the feature extraction

methods by producing compact classes. Our

experimental results on simulated data illustrated

that the proposed methods improve the performance

of the SVM classifier both in terms of accuracy and

complexity. These results also illustrated that LDA

provides slightly improved generalization compared

to PCA and ICA. Experimental results on a facial

database demonstrated the same improvement in

classification performance using LDA extracted

features. In our future work, we plan to evaluate the

performance of adaptive PCA and LDA algorithms

for feature extraction in facial data.

REFERENCES

Sun, Z., Bebis, G., Miller, R., 2004. Object detection using

feature subset selection. Pattern Recognition, Elsevier

Vol. 37, No. 11, pp. 2165-2176

Jain, A., Duin, R., Mao, J., 2001. Statistical pattern

recognition: a review. IEEE Trans. Pattern Anal.

Machine Intell , Vol. 22, No. 1, pp. 4-37

Belhumeur, P. N., Hespanha, J. P., Kriegman, D. J., 1997.

Eigenfaces vs. Fisherfaces: Recognition using class

specific linear projection. IEEE Trans. Pattern Anal.

Machine Intell , Vol. 19, pp. 711-720.

Moghaddam, B., 2002. Principal manifolds and

probabilistic subspaces for visual recognition. IEEE

Method Mean of

Margin

Mean of SV Mean of

Recognition

Rate

No subspace 0.2027 126.8 95.33

PCA 0.2201 120.9 96.50

ICA 0.2247 122.0 96.52

LDA 0.2745 120.0 96.94

PCA iterative 1.2032 10.1 98.5

ICA iterative 1.1547 10.6 97.5

LDA iterative 1.3521 9.5 98.9

VISAPP 2006 - IMAGE ANALYSIS

484

Trans. Pattern Anal. Machine Intell, Vol. 24, No. 6,

pp. 780-788.

Othman, H., Aboulnasr, T., 2003. A separable low

complexity 2D HMM with application to face

recognition. IEEE Trans. Pattern Anal. Machine

Intell, Vol. 25, No. 10, pp. 1229-1238

Er, M. J., Wu, S., Lu, J., Toh, H.L., 2002. Face recognition

with radial basis function (RBF) neural networks.

IEEE Trans. Neural Networks, Vol. 13, No. 3, pp. 697

– 710.

Lee, K., Chung, Y., Byun, H., 2002. SVM-based face

verification with feature set of small size. Electronics

Letters, Vol. 38, No. 15, pp. 787-789

Turk, M., Pentland, A., 1991. Eigenfaces for recognition.

J. Cognitive Neurosci

Liu, C., Wechsler, H., 2003. Independent component

analysis of Gabor features for face recognition. IEEE

Trans. Neural Networks, Vol. 14, No. 4, pp. 919-928

Yu, H., Yang, J., 2001. A direct LDA algorithm for high

dimensional data―with application to face

recognition. Pattern Recognition

, Vol. 34, No. 10, pp.

2067-2070

Heisele, B., Ho, P., Poggio, T., 2001. Face recognition

with support vector machines: global versus

component-based approach. Proceedings of the 8

IEEE International Conference on Computer Vision

,Vol. 2, pp. 688 - 694

Vapnik, V., 1995. The nature of statistical learning

theory. ,Springer, Berlin.

Wang, Y., Chua, C. S., Ho, Y. K., 2002. Facial feature

detection and face recognition from 2D and 3D

images. Pattern Recognition Letters, Vol. 23, No. 10,

pp. 1191-1202

Qi, Y., Doermann, D., DeMenthon, D.,2001. Hybrid

independent component analysis and support vector

machine learning scheme for face detection.

Proceedings of the International Conference on

Acoustics, Speech and Signal Processing (ICASSP),

pp. 3327–3338

Fortuna, J., Capson, D., 2004. Improved support vector

classification using PCA and ICA feature

space

modification. Pattern Recognition, Vol. 37, No. 6, pp.

1117-1129

Bartlett, M., Sejnowski, T.,1997. Independent components

of face images: a representation for face recognition.

Proceedings of the Fourth Annual Joint

Symposium on

Neural Computation

Shi, Z., Tang, H., Tang, Y., 2004. A new fixed-point

algorithm for independent component analysis

. Neuro-

computing , Vol. 56, pp. 467- 473.

Cristianini, N., Shawe-Taylor, J., 2000. An Introduction to

Support Vector Machines. Cambridge University

Press

Georghiades, S., Belhumeur, N., Kriegman, D. J., 2001.

From few to many: illumination cone models for face

recognition under variable lighting and pose. IEEE

Trns, Pattern Anal, Machine Intell, pp. 643-660.

Fukunaga, K., 1990. Introduction to Statistical Pattern

Recognition, Academic Press,New York . 2

edition.

FACIAL IMAGE FEATURE EXTRACTION USING SUPPORT VECTOR MACHINES

485