
INTERPOLATION SNAKES FOR BORDER DETECTION IN
ULTRASOUND IMAGES
Silviu Minut
Michigan State University
East Lansing, MI, USA
George Stockman
Michigan State University
East Lansing, MI, USA
Keywords:
snakes, active contours, ultrasound, echocardiogram, border detection, segmentation, left ventricle, interpola-
tion splines, energy minimization.
Abstract:
Ultrasound images present major challanges to just about any segmentation algorithm, including active contour
techniques, due to increased specularity, non-uniform edges along the boundaries of interest, incomplete and
misleading visual support. Active contours that depend on a vector of parameters (e.g. B-splines), have been
proposed in the literature, and have the advantage over traditional snakes and level-set snakes, that smoothness
is built-in, which is a sine qua non requirement in border detection in medical images. We propose in this
paper the use of interpolation splines as active contours for border detection in ultrasound images, which
we term interpolation snakes. We argue that interpolation snakes are better suited for ultrasound than other
snakes, because of the fact that the control points (parameters which control the shape of the snake) are on
the curve. This allows for an initial arclength parameterization of the snake. In conjunction with interpolation
snakes we define a new energy (measure of fit) which incorporates a term supposed to maintain arclength
parameterization of the snake throughout the minimization process. A shape prior can also be introduced
naturally, as a distribution on the control points.
1 INTRODUCTION
Active contours have been used extensively in many
computer vision problems, particularly in boundary
detection and motion tracking, with relative success,
especially in medical imaging. Almost two decades
after the introduction of the concept by Kass, Witkin
and Terzopoulos (Kass et al., 1988), a great variety
of different “species” of snakes have been developed.
One can distinguish two major categories: variational
models, and geometric models.
Chronologically, the variational models occured
first (Kass et al., 1988), and are based on the observa-
tion that if we want a curve γ to be aligned along the
edges in an image, then γ must accumulate the most
amount of gradient. In other words, γ must minimize
an image energy defined as:
E
img
(γ)=−
γ
|∇I|ds (1)
If smooth minima are sought, then an extra energy
term must be added into the equation, to penalize for
the formation of discontinuities:
E
int
(γ)=
γ
|γ
|
2
+ |γ
|
2
ds (2)
The original Kass, Witkin and Terzopoulos active
contour model includes a third energy term - the ex-
ternal energy E
ext
, which can incorporate e.g. prior
knowledge about the location or the shape of the
boundaries of interest. One then seeks minima of an
energy functional of the form
E(γ)=E
img
+ E
int
+ E
ext
(3)
Minimization of the energy (3) is done through
variational principles and so local minima are found.
Consequently, initialization near the boundaries of in-
terest is required. This model underwent major im-
provements (themselves variational models) e.g. in
(Cohen, 1991; Amini et al., 1990; Williams and Shah,
1992; Xu and Prince, 1997; McInerney and Terzopou-
los, 2000), only to quote a few.
The geometric models were introduced indepen-
dently in (Caselles et al., 1993) and (Malladi et al.,
1995) based on front propagation theory (Osher and
Sethian, 1988; Osher and Sethian, 1990) and were a
297
Minut S. and Stockman G. (2006).
INTERPOLATION SNAKES FOR BORDER DETECTION IN ULTRASOUND IMAGES.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 297-305
DOI: 10.5220/0001364202970305
Copyright
c
SciTePress

revolutionary way of viewing active contours. These
authors proposed a non-variational approach, namely
mean curvature motion along the normal direction.
By viewing the active contour as the zero level-set of a
surface φ = φ(x, y, t), the motion of the snake along
its own normal direction can be cast into a Hamilton-
Jacobi (H-J) evolution equation φ
t
= H(∇φ). The
existence of solutions of H-J equations, their proper-
ties, as well as numerical schemes for finding them,
are highly non-trivial mathematical subjects. Thanks
to the deep results of (Crandall and Lions, 1984; Os-
her and Shu, 1991; Sethian, 2001), there are known
numerically stable schemes that can be used to solve
H-J equations. Efficient algorithms such as the fast
marching method (Sethian, 1996) and the narrow
band method (Adalsteinsson and Sethian, 1995) have
also been found, and make the level-set snakes suit-
able for real-time applications. A milestone in the
theory of active contours was the introduction of geo-
desic active contours by Caselles, Kimmel and Sapiro
(Caselles et al., 1997), which provide a unifying view
of the variational and non-variational models, and
are arguably the state-of-the-art in active contours.
Specifically, it is shown in this work that the minima
of a gradient-based energy derived from (3) can be
obtained through motion in the normal direction, and
hence, implemented using level sets, these snakes can
change topology during evolution.
There are, important domains, such as ultrasound,
which provide very irregular visual support for the
boundaries of the object of interest, while the true
boundaries are known a priori to be smooth. See Fig-
ure 1. Ultrasound is one of the toughest domains in
computer vision, and still presents great challanges to
just about any segmentation or border detection algo-
rithm, due to the noisy, specular nature of the ultra-
sound images and incomplete data, with misleading
visual support. The edges in such images are usually
weak, spurious, and have non-uniform magnitude.
Under these extreme conditions, variational models
usually follow the data too closely, and the detected
boundaries do not meet the smoothness requirement.
Geometric models pose additional problems. Their
signature feature - the ability to seamlessly change
topology - is detrimental in ultrasound, because the
snake can and will detect artifacts, muscles or other
visually salient structures which are not in fact part
of the object of interest. Another problem with geo-
metric snakes - perhaps the most stringent under the
conditions of non-uniform boundaries - is the stop-
ping criterion: the snake may stop prematurely in
some regions, while leaking through the boundaries
in other places. These problems are illustrated in Fig-
ure 1 (b)
1
. The snake stops around the inner structure
1
Using the ITK (Kitware, 2005) implementation of the
geodesic active contour model.
(papillary muscle) while it leaks through the valve,
and near the apex. More often than not, a single set of
parameters, regardless of their values, simply cannot
accomodate both strong and very weak boundaries
along the same contour.
What can be done, however, if smooth boundaries
are required in noisy images, is to search for minima
of the energy (3) in a (finite dimensional) subspace
of the space of all curves. One way to do this is to
choose a finite set of functions (with certain desirable
properties), and consider only snakes which are linear
combinations of those basis functions:
γ
C
(s)=
l
i=1
c
i
·B
i
(s) (4)
The search space is now reduced to span < B
i
>≈
R
2l
, and the restriction to this space of any snake en-
ergy function is now simply a function of 2l variables.
The shape of any γ = γ
C
is controlled by the vector
C =(c
1
,...c
l
) ∈ R
2l
of free parameters.
Several varieties of snakes fall in this framework.
Staib and Duncan (Staib and Duncan, 1992) express
a closed curve in the form of a trigonometric series,
and then, to reduce the number of degrees of free-
dom, they truncate the series to the first n harmon-
ics, where n is a finite, user-defined integer. Along
the same lines, Jain et al. (Jain et al., 96) use prod-
ucts of the form sin nt · cos mt as basis functions. B-
Splines (de Boor, 2001) were used as active contours
(B-Snakes) for border detection and tracking (Bascle
and Deriche, 1992; Brigger et al., 2000; Rueckert,
1997), and for stereo problem (Menet et al., 1990).
Cootes and Taylor (Cootes et al., 1995) learn the
modes of variation of the outline of an object of in-
terest and express the snake as a linear combination
of the most significant modes. Regarding the selec-
tion of the number of free parameters that define the
snake, Figueredo (Figueredo et al., 2000) proposes
a very powerful, fully automatic way of determin-
ing this number, using a minimum description length
(MDL) criterion.
Parametric snakes are best suited for problems
where smoothness is a must. In addition to that, they
preserve topology, which, in medical images, is often
known a priori. Furthermore, prior knowledge about
the shape of the snake can be introduced in a more
natural way, as prior probability on the coefficients,
and can be done so in a way invariant to translations,
rotations and scale (Cremers et al., 2003) (although
very recently, shape prior has been introduced in level
sets too by Leventon et al. in (Leventon et al., 2000),
and Cremers et al. in (Cremers et al., 2004)). Last,
but not least, from a practical standpoint, minimiza-
tion of an energy like (3) is a much more tractable
problem in the case of parametric snakes: such an en-
ergy is simply a function of 2l variables, and can be
VISAPP 2006 - IMAGE ANALYSIS
298
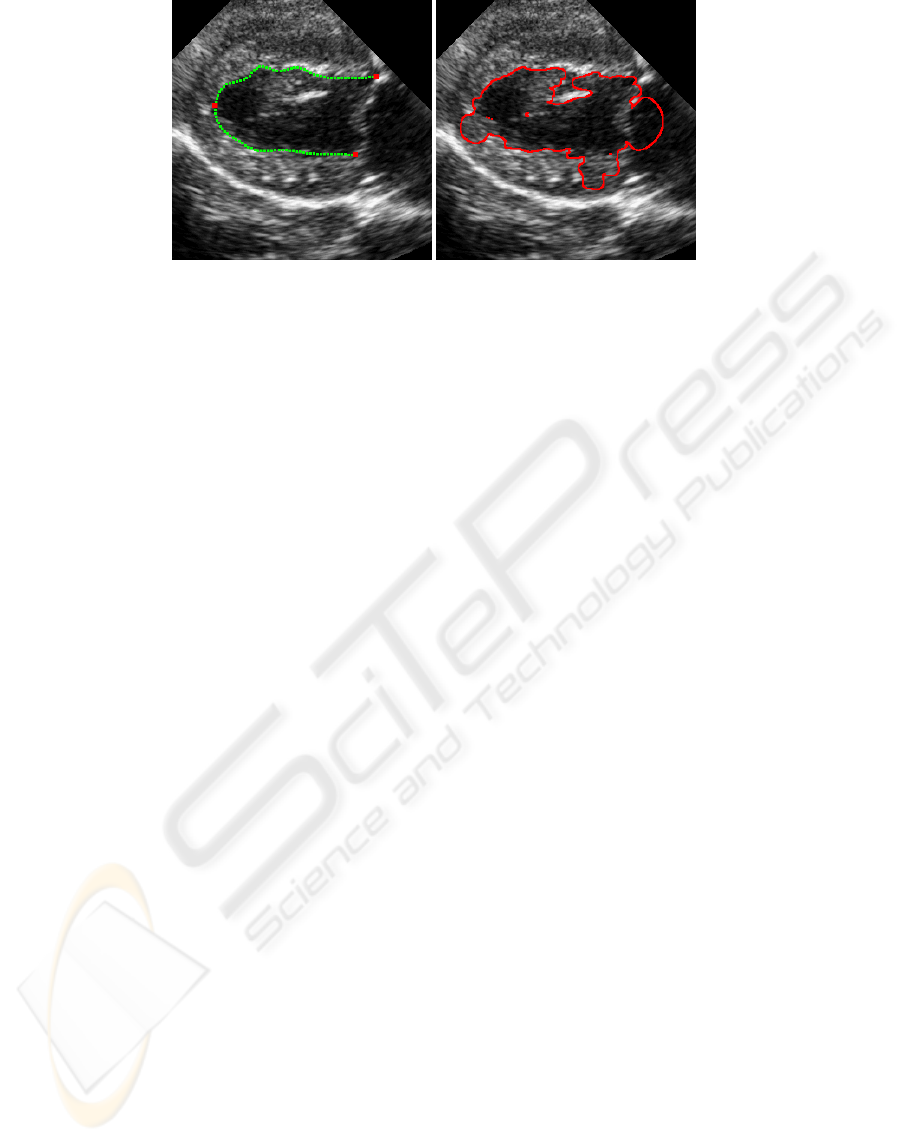
(a) (b)
Figure 1: Endocardium detection in an echocardiogram (dog heart). (a) Green: manually drawn ground truth. The red dots
represent the all important valve points and apex. (b) Segmentation using the Geodesic Acrive Contour model. Note the
ruggedness and the leakage through regions of low gradient, while stopping at extraneous anatomical structures inside the
ventricle.
minimized by any of a number of well tested, already
existing minimization algorithms. No special provi-
sions must be made to ensure the numerical stability
of the evolution problem.
2 INTERPOLATION SNAKES
We have argued that parametric snakes are likely to
work better in difficult environments, such as ultra-
sound. Of these snakes, we shall single out one par-
ticular type, most suitable for imposing spatial hard
constraints.
There are situations where certain points or regions
along the boundary of interest have particular signif-
icance for the problem at hand, and so, they have to
be very accurately located. Such is the case, for in-
stance, with the two valve points and the apex of the
left ventricle, in echocardiograms (See Figure 1 (a)).
However, when these spots happen to lie along weak
edges or incomplete data, or simply in a region that
does not differ qualitatively from other regions along
the border, they are nearly impossible to detect by a
“simple-minded” data fitting snake.
Short of implementing special purpose modules
dedicated to the sole detection of these special points,
a compromise solution might be to allow an expert
user to mark these points as fixed at initialization time.
These fixed points are hard constraints for an evolving
active contour and we argue that among the various
types of smooth snakes, interpolation snakes are the
most amenable to imposing hard constraints.
Following (de Boor, 2001), an interpolation spline
is defined in 2D by the following elements:
• a strictly increasing set of real numbers ξ
0
<
ξ
1
···<ξ
l
(the break points),
• a set (with the same number of elements) of data
vectors: y
0
,...y
l
∈ R
2
(the control points).
• a positive integer k (the degree of the spline).
Given this data, the interpolation spline of degree
k, is defined as a curve γ :[ξ
0
,ξ
l
] → R
2
, with the
following properties:
• componentwise, γ is a degree-k polynomial on
each interval [ξ
i
,ξ
i+1
)
• the pieces fit smoothly at the break points: γ is of
class C
k−1
, i.e. it has k − 1 continuous derivatives.
By fixing the break points and the degree, the
free parameters that define the spline are the control
points, and these are points on the spline, by defini-
tion. This distinguishes the interpolation splines from
other types of parametric snakes, where the parame-
ters do not have an intuitive geometric significance,
and makes interpolation splines suitable for imposing
spatial hard constraints. Indeed, with other types of
parametric snakes, it is not obvious what conditions
should be imposed on what coefficients, in order e.g.
to force the snake to go through a fixed point.
Of particular importance are the cubic interpola-
tion splines (k =3), due to the following property
(de Boor, 2001): among all smooth curves (polyno-
mial or otherwise) that pass through the given control
points at the respective break points, cubic interpo-
lation splines have the smallest total second deriva-
tive, i.e. they are minima of
ξ
l
ξ
0
γ
(τ)
2
dτ, subject
to the constraints γ(ξ
i
)=y
i
for all i. Note that
one minimizes the total second derivative (as opposed
to other derivatives), because of its geometric signif-
icance: under the canonical parametrization, the sec-
ond derivative represents the curvature of γ, and so, it
INTERPOLATION SNAKES FOR BORDER DETECTION IN ULTRASOUND IMAGES
299

measures the amount of bending at each point on the
curve.
The snake energy is a function of the control points:
E = E(y
0
,...y
l
), and we fit an interpolation snake
to an image, by varying the control points. Obvi-
ously, if any of these points must remain fixed dur-
ing the minimization, we simply consider the energy
as a function of the remaining control points (but the
spline is still computed through the entire set of con-
trols).
Computation of a cubic interpolation spline is
based on the following lemma. See e.g. “Recipes in
C” (Press et al., 1993):
Lemma 2.1 If γ = γ(t) is a cubic polynomial, then
on any interval [a, b] γ can be expressed uniquely as
γ(t)=A(t) · γ(a)+B(t) · γ(b)
+ C(t) · γ
(a)+D(t) · γ
(b)
(5)
where
A =
b − t
b − a
,B=1− A
C =
(A
3
− A)(b − a)
2
6
,D=
(B
3
− B)(b − a)
2
6
If we take a, b to be consecutive breakpoints, say,
a = ξ
i
and b = ξ
i+1
, then, since γ(ξ
i
)=y
i
and
γ(ξ
i+1
)=y
i+1
are control points (hence given), we
can compute γ(t) for all t ∈ [ξ
i
,ξ
i+1
], provided we
know the second derivatives γ
at the break points.
The second major point is, therefore, the computa-
tion of γ
(ξ
j
):=γ
j
, for j =0,...l− 1. This can be
done by taking the derivative in (5) and requiring that
the first derivatives of γ be continuous at the break
points. In the case of a closed spline, this condition
makes sense at all l break points, if we identify natu-
rally y
l
= y
0
,y
−1
= y
l−1
and ξ
l
= ξ
l−1
+ |γ
l−1
γ
0
|.
We get then a linear l × l system in the unknowns γ
j
(one system in each dimension of γ) whose matrix has
the form
M =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
A
0
B
0
0 ... 00C
l−1
C
0
A
1
B
1
... 000
0 C
1
A
2
... 000
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000... A
l−3
B
l−3
0
000... C
l−3
A
l−2
B
l−2
B
l−1
00... 0 C
l−2
A
l−1
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
Lemma 2.2 M has an LU decomposition M = LU .
Proof: The proof is straightforward once we guess
the right form of L and U:
L =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
100... 0000
b
0
10... 0000
0 b
1
1 ... 0000
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000... b
l−4
100
000... 0 b
l−3
10
u
0
u
1
u
2
... u
l−4
u
l−3
b
l−2
1
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
U =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
a
0
b
0
0 ... 00v
0
0 a
1
b
1
... 00v
1
00a
2
... 00v
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000 0b
l−4
0 v
l−4
000 0a
l−3
b
l−3
v
l−3
000 0 0 a
l−2
b
l−2
000 0 0 0 a
l−1
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
In the case of an open spline, the continuity of the
first derivative only makes sense at the l − 2 interior
break points, and we set γ
(ξ
0
)=γ
(ξ
l−1
)=0for
two extra conditions. The resulting system is in this
case genuinely tridiagonal. Thus, in either case, the
second derivatives can be computed in O(l) time. If
the curve is sampled at n points, then computation of
the interpolation spline has complexity O(l + n)=
O(n),asl<n.
3 THE ENERGY FUNCTIONAL
Obviously, since smoothness is built into γ
C
, we can
drop the internal energy term E
int
from the energy
(3). Our only concerns now are (a) to make the snake
converge to boundaries, (b) keep the points equidis-
tant during the evolution and, eventually, (c) impose
a prior on the overall shape of the snake, e.g. in the
form of a density function on the control vector C,or
using kernel methods as in (Cremers et al., 2003). Un-
der these requirements, we model the snake evolution
by the following energy:
E(C)=
γ
w(s)· < ∇I
⊥
,
γ
|γ
|
>
E
img
+
L
0
||γ
(t)|−1|dt
E
arc
+ E
shape
(6)
Here, <, >denotes the dot product, C =
(y
0
,...y
l−1
) ∈ R
2l
is again the vector of control
VISAPP 2006 - IMAGE ANALYSIS
300

points of the spline, L = length(γ), and w(s) is a
user-defined weight function along γ.
The image energy E
img
measures the fit to data.
In the simplest case, w ≡ 1, in which case, if we
fix an orientation along γ, the spline will align itself
along edges with dark to its right, and light to its left.
The reason for this is that < ∇I
⊥
,
γ
|γ
|
> is minimum,
when ∇I
⊥
is coliniar with γ
and points in the op-
posite direction. This means that the gradient itself
points from right to left as we walk along γ in the
direction of the chosen orientation.
An illustrative example of the general case is shown
in Figure 3. The green curves represent the initial (a)
and final (b) interpolation snake. A blue circle rep-
resents a control point with w =0and will be kept
fixed during the minimization. The variable points
are marked in red, either with a plus sign (w =+1)
or with a minus sign (w = −1). The energy (6) is a
function of the red control points only. The weights at
any other point on the spline (green points) are com-
puted by interpolation of the known weights. In this
example, the orientation of the spline is from top to
bottom. Although initialized on an edge, the snake
moves away from it, picking the edges with the po-
larity dictated by the weights: as we walk downward
along the final snake (b), the w<0 points are at-
tracted by a dark → light edge, whereas points with
w>0 are attracted by a light → dark edge. This
edge polarity selection by the snake is due to the fact
that unlike the image energy E
img
in (3) which only
depends on the magnitude of the gradient, the E
img
in (6) depends on the magnitude of the gradient and
on the angle between the gradient ∇I and the (unit)
tangent to γ. We have found that this latter image en-
ergy performs better than the original magnitude-only
image energy.
(a) Initial (b) Final
A final detail about E
img
is the computation of the
image gradient ∇I. Instead of the usual gaussian
smoothing, or the more sophisticated anisotropic
smoothing methods, we compute the directional
derivatives at each pixel as I
x
= average(I)
right
−
average(I)
left
and I
y
= average(I)
bottom
−
average(I)
top
, where each average intensity is cal-
culated on a small rectangle in constant time (only 4
lookup operations, regardless of the size of the rectan-
gle), using a pre-computed integral map of the image
I (Viola and Jones, 2004). Obviously, if a different
amount of smoothing is deemed necessary, the inte-
gral map need not be computed again.
The arclength energy E
arc
is designed to keep the
points of the snake equidistant throughout the mini-
mization process, by penalizing non-arclength para-
meterizations. Since under the canonical parameter s,
the speed along the curve is 1 (i.e. |γ
(s)| =1), then
the amount
|γ
(τ)|−1
is indicative to which extent
τ fails to be the canonical parameter. The necessity of
the arclength term is due to the following argument.
Without exception, a curve γ is discretized by sam-
pling it at equally spaced grid points t
i
= i·∆t.How-
ever, the points γ
i
= γ(t
i
) need not be equidistant, so
this procedure does not correspond to the arclength
parameterization. Of course, if a non-uniform distri-
bution of the points along the snake is allowed, then
the image energy will indicate a misleading measure
of fit, if e.g. a densely populated segment along the
snake happens to fall into an energy pit. It is therefore
crucial to start out with, and maintain equally spaced
points on the snake.
Somewhat surprisingly, the problem of preserving
arclength parametrization along the snake during the
evolution, although noticeable both theoretically and
practically, has been silently overseen. Different ac-
tive contours implementations deal with this problem
in an ad-hoc manner, e.g. by removing points from
regions along the snake where the points have come
too close together, and inserting points in regions
where the snake has become too sparse. The first au-
thors to address this problem were, to our knowledge,
Williams and Shah (Williams and Shah, 1992), who
replace the first order term in the internal energy E
int
(2), by a term which penalizes for deviations from the
mean distance
¯
d =
|γ
i+1
− γ
i
|/n along the con-
tour, namely
(|γ
i+1
− γ
i
|−
¯
d|).
In the discrete setting, we take an equidistant sub-
division of the interval [0,L], namely τ
i
= i · L/n,
and let γ
i
= γ
C
(τ
i
). We approximate the derivative
at τ
i
as γ
(τ
i
) ≈ (γ
i+1
− γ
i
)/∆τ, and approximate
the arclength energy E
arc
by a Riemann sum:
E
arc
≈
n−1
i=0
|γ
i+1
− γ
i
|
∆τ
− 1
· ∆τ (7)
=
n−1
i=0
|γ
i+1
− γ
i
|−∆τ
(8)
If L is chosen to approximate the length of the (ini-
tial) contour, and if this length remains roughly the
INTERPOLATION SNAKES FOR BORDER DETECTION IN ULTRASOUND IMAGES
301
same during the evolution, then
n−1
i=0
|γ
i+1
− γ
i
|≈L = n · ∆τ
so ∆τ is the mean of all distances between consecu-
tive points along the snake. We arrive this way at the
elastic energy proposed by Williams and Shah.
The initial snake is also constructed so that the sam-
pling at uniform time intervals corresponds to (an ap-
proximate) arclength parameterization. We achieve
this by a judicious choice of the break points ξ
i
.Ify
i
are the user-defined control points, then we choose
ξ
0
=0, and ξ
i
− ξ
i−1
= |y
i
y
i−1
| for i>0,so
that the length along the curve between two consec-
utive control points y
i−1
and y
i
is approximated
2
by
∆ξ = ξ
i
− ξ
i−1
. By choosing the breaks this way,
the usual (uniform) parameter t along the real axis,
becomes - approximately - the arclength parameter
along the resulting spline γ = γ(t). Note that this
choice of the breakpoints, which seamlessly produces
a curve parametrized approximately by arclength, is
not possible with other parametric snakes; it is only
possible with interpolation snakes, because of the par-
ticular significance of the snake parameters, as points
on the snake.
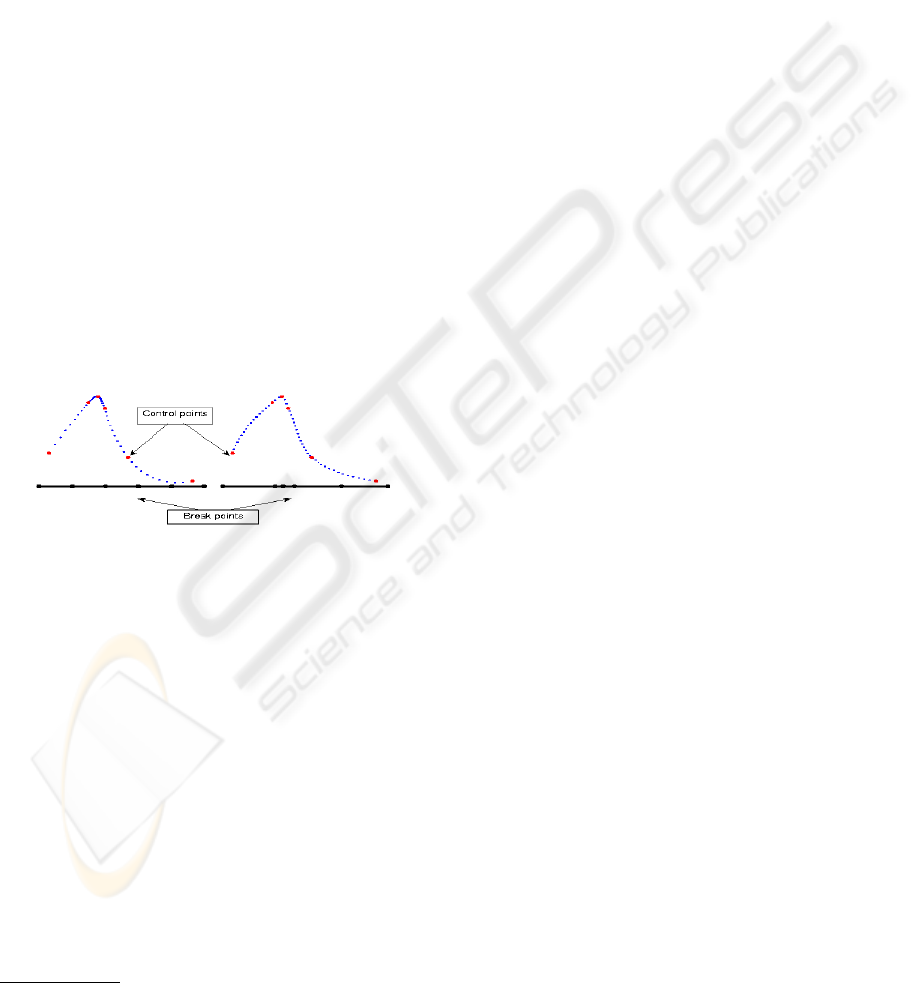
Figure 2: Cubic interpolation spline (blue). Red: control
points. Black: break points. The spline on the left has
equidistant breaks, and is not parametrized by arclength (the
density is higher near points of high curvature). The spline
on the right is built on the same control points as the one on
the left. Choosing the breaks ξ
i
by ξ
i
= ξ
i−1
+ |y
i−1
y
i
|
produces an arclength parameterized spline.
The shape energy E
shape
represents the shape
prior knowledge and can be imposed e.g. as a distrib-
ution on the vector of coefficients. Any of a number
of techniques for distribution estimation can be used,
such as e.g. Principal Component Analysis (PCA) on
a number of training contours, Parzen windows, or
more general kernel methods (Cremers et al., 2003;
Cremers et al., 2004). In this paper we use the sim-
plest method: we simply assume a Gaussian distrib-
ution on the control points, estimated using the full
2
To the extent that the segment y
i−1
y
i
approximates the
corresponding arch along the spline.
covariance matrix and the mean of manually anno-
tated training contours. Since the number of control
points is small (e.g. 15 control points), we need not re-
duce the dimension through PCA. We assume known
correspondences on the control points of the training
samples. During the minimization, we factor out the
scale, translation and the rotation of the active con-
tour, by registering it to the mean of the training sam-
ples.
We minimize the energy (6) using Powell’s con-
jugate directions gradient descent algorithm (Press
et al., 1993).
4 RESULTS
A systematic comparison of various active contour al-
gorithms on a significant database of (medical) im-
ages is beyond the scope of this paper, and will be
the subject of another study. For now we shall con-
fine ourselves to three examples. We only compare
our interpolation snakes against the geodesic snakes
(Caselles et al., 1997).
Example 1. For this example refer to Figure 3. A
synthetic binary image is used as ground truth (Fig-
ure 3 (a)). We we simulate a noisy boundary by ran-
domly swapping pixels. Figures 3 (b) and (c) show
the initial and the final interpolation snake. As be-
fore, the red points are variable, and the blue circles
are fixed points. A single interpolation spline, cannot
make sharp turns, by construction. However, since we
allow for open interpolation snakes, nothing prevents
us from defining a chain of independent snakes (2 in
this example), such that each snake starts precisely
where the previous one ended. Obviously, at the joints
(blue circles) the aggregate snake has no smoothness
(other than continuity), being able this way to simu-
late sharp corners. Figure 3 shows in red the geodesic
active contour. Since it is impossible to keep fixed
points during the evolution of the geodesic snake, the
lower wedge is missed.
Example 2. This example shows the performance
of an interpolation snake vs. a geodesic active contour
in a cardiac ultrasound image. Refer to Figure 4. Parts
(a) and (c) show two significantly different initializa-
tions, and (b) and (d) show the detected epicardium.
Part (i) is the geodesic active contour. The rugged
shape and leakage through the boundary are typical
for geodesic snakes (and other non-spline snakes) in
ultrasound.
Example 3. Certainly, our interpolation snake is
not fail proof. It was designed to detect smooth
edges, but, like any other snake, without any fur-
ther constraints it does not have control upon which
edges to detect (other than the polarity of the edges,
as explained in the example in Section 3). For this
VISAPP 2006 - IMAGE ANALYSIS
302
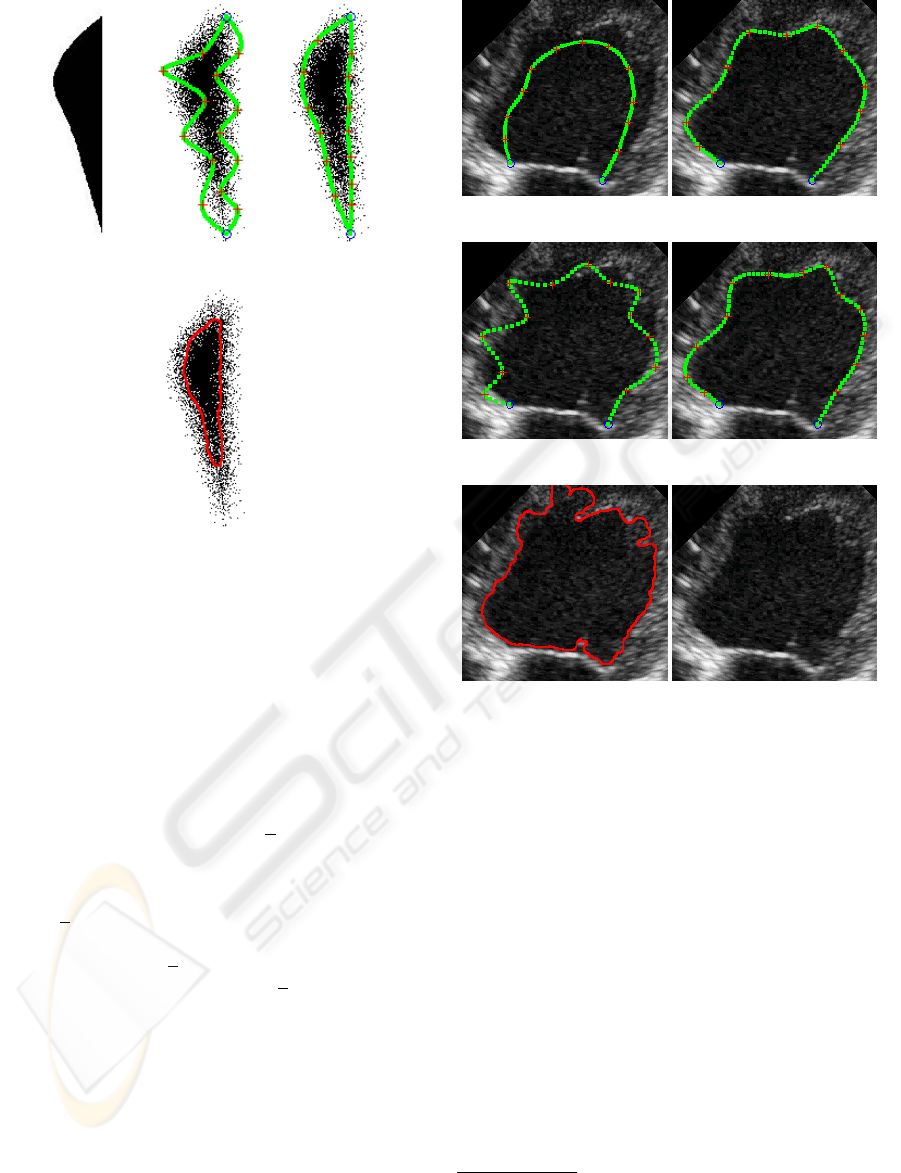
(a) (b) (c)
(d)
Figure 3: Comparison to ground truth in a synthetic image.
(a) Ground truth image. (b) Initialization of a 2-piece ag-
gregate interpolation snake. Each piece starts and ends at a
blue circle (fixed control point). (c) Detected boundary. (d)
Geodesic active contour.
last example refer to Figure 5. Here we incorpo-
rate prior knowledge about the shape of the target
object (ellipse). For training we generate 30 inter-
polation splines z
i
, 12 control points each, from a
gaussian distribution, whose mean
z approximates an
ellipse. We assume known correspondences between
the control points of any two training samples. If W
is the working snake, then we take E
shape
(W )=
− log N(
z,25)(w) where N(·, ·) is the normal dis-
tribution and w is obtained from W by registering
the latter to the mean
z by a scaling transformation,
using the control points of W and
z. As expected,
using the shape prior, the snake no longer detects ar-
bitrary edges (as in Figure 5 (b)), but only the ellipse
(Figure 5 (d)).
5 CONCLUSION
We have introduced in this paper a new type of active
contour - the interpolation snake - designed to detect
smooth boundaries in very noisy images, with non-
uniform gradient along edges, such as ultrasound.
(a) (b)
(c) (d)
(e) (f)
Figure 4: Application to ultrasound. (a) and (c) Initial inter-
polation snake. (b) and (d) Detected boundary. (e) Geodesic
active contour. (f) Original image used in (a)-(e).
This type of snake is in the same category as B-
Snakes. The lack of the compact support property
3
does not seem to affect the performance of an in-
terpolation snake, while due to the particular signif-
icance of the control points, our snake has other at-
tractive properties, such as arclength parameterization
throughout the fitting process, and the ability to freeze
some of the control points. Prior knowledge can be
introduced naturally, as a distribution on the control
points.
3
A control point on a B-Snake can change the shape of
the curve only in a local neighborhood, because the basis
functions have compact support. This is not the case with
an interpolation snake.
INTERPOLATION SNAKES FOR BORDER DETECTION IN ULTRASOUND IMAGES
303

(a) (b)
(c) (d)
(e)
Figure 5: Interpolation snakes without shape prior((a),(b))
and with shape prior ((c),(d)). (e) Aligned training contours
(green) and their mean (purple).
ACKNOWLEDGEMENTS
We are greateful to Dr. Bari Olivier and Dr. Au-
gusta Pelosi from the MSU Animal Clinic for pro-
viding us with echocardiograms of the dog heart.
We also thank Kitware Inc. - the producer of the
Insight Toolkit (ITK) - for making publically avail-
able their wonderful software. We have used ITK’s
Geodesic Active Contours.
REFERENCES
Adalsteinsson, D. and Sethian, J. A. (1995). A fast level set
method for advancing interfaces. Journal of Compu-
tational Physics, 118(2):269–277.
Amini, A. A., Weymouth, T. T., and Jain, R. C. (1990).
Using dynamic programming for solving variational
problems in vision. PAMI, 12(9):855–867.
Bascle, B. and Deriche, R. (1992). Feature extraction us-
ing parametric snakes. In Proceedings of the 11-th
IAPR International Conference on Pattern Recogni-
tion, pages 659–663, Netherlands.
Brigger, P., Hoeg, J., and Unser, M. (2000). B-spline
snakes: A flexible tool for parametric contour de-
tection. IEEE Transactions on Image Processing,
9(9):1484–1496.
Caselles, V., Catte, F., Coll, T., and Dibos, F. (1993). A geo-
metric model for active contours. Numerische Mathe-
matik, 66:1–31.
Caselles, V., Kimmel, R., and Sapiro, G. (1997). Geodesic
active contours. International Journal of Computer
Vision, 22(1):61–79.
Cohen, L. (1991). On active contour models and balloons.
CVGIP: Image Understanding, 53(2):211–218.
Cootes, T., Taylor, C. J., Cooper, D. H., and Graham, J.
(1995). Active shape models - their training and ap-
plication. Computer Vision and Image Understanding,
61(1):38–59.
Crandall, M. and Lions, P. (1984). Two approximations of
solutions to Hamilton-Jacobi equations. Mathematics
of Computation, 43(167):1–19.
Cremers, D., Kohlberger, T., and Schnorr, C. (2003). Shape
statistics in kernel space for variational image seg-
mentation. Pattern Recognition, 36(9):1929–1943.
Cremers, D., Osher, S., and Soatto, S. (2004). Kernel den-
sity estimation and intrinsic alignment for knowledge-
driven segmentation: Teaching level sets to walk. Pat-
tern Recognition, 3175:36–44.
de Boor, C. (2001). A Practical Guide to Splines. Springer.
Figueredo, M., Leitao, J., and Jain, A. (2000). Unsuper-
vised contour representation and estimation using b-
splines and a minimum description length criterion.
IEEE Transactions of Image Processing, 9(6):1075–
1087.
Jain, A., Zhong, Y., and Lakshmanan, S. (96). Object
matching using deformable templates. IEEE PAMI.,
18(3):267–278.
Kass, M., Witkin, A. P., and Terzopoulos, D. (1988).
Snakes: Active contour models. IJCV, 1(4):321–331.
Kitware (2005). The Insight Segmentation and Registration
Toolkit (ITK). http://www.itk.org.
Leventon, M. E., Grimson, W. E. L., and Faugeras, O.
(2000). Statistical shape influence in geodesic active
contours. In IEEE Proceedings of CVPR, volume 1,
pages 316–323, Hilton Head Island, North Carolina.
Malladi, R., Sethian, J., and Vemuri, B. (1995). Shape mod-
eling with front propagation: A level set approach.
PAMI, 17(2):158–175.
McInerney, T. and Terzopoulos, D. (2000). Topology adap-
tive snakes. Medical Image Analysis, 4:73–91.
VISAPP 2006 - IMAGE ANALYSIS
304

Menet, S., Saint-Marc, P., and Medioni, G. (1990). B-
snakes: Implementation and application to stereo. In
DARPA90, pages 720–726.
Osher, S. and Sethian, J. A. (1988). Fronts propagating
with curvature-dependent speed: Algorithms based on
Hamilton-Jacobi formulations. Journal of Computa-
tional Physics, 79:12–49.
Osher, S. and Sethian, J. A. (1990). Recent numerical
algorithms for hypersurfaces moving with curvature-
dependent speed: Hamilton-Jacobi equations and con-
servation laws. Journal of Differential Geometry, 31,
pp. 131–161, 1990, 31:131–161.
Osher, S. and Shu, C.-W. (1991). High-order essentially non
oscillatory schemes for Hamilton-Jacobi equations.
Siam Journal of Numerical Analysis, 28(4):907–922.
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vet-
terling, W. T. (1993). Numerical Recipes in C:
The Art of Scientific Computing. Cambridge Univer-
sity Press, 2nd edition edition. available online at
http://www.nr.com.
Rueckert, D. (1997). Segmentation and Tracking in Car-
diovascular MR Images Using Geometrically De-
formable Models and Templates. PhD thesis, De-
partment of Computing, Imperial College of Science,
Technology and Medicine, London.
Sethian, J. (2001). Level Set Methods and Fast March-
ing Methods. Cambridge Monographs on Applied
and Computational Mathematics. Cambridge Univer-
sity Press, 2 edition.
Sethian, J. A. (1996). A fast marching level set method
for monotonically advancing fronts. Proc. Natl. Acad.
Sci. USA, 93:1591–1595.
Staib, L. and Duncan, J. S. (1992). Boundary find-
ing with parametrically deformable models. PAMI,
14(11):1061–1075.
Viola, P. and Jones, M. (2004). Robust real-time face detec-
tion. IJCV, 57(2):137–154.
Williams, D. J. and Shah, M. (1992). A fast algorithm for
active contours and curvature estimation. CVGIP: Im-
age Underst., 55(1):14–26.
Xu, C. and Prince, J. (1997). Gradient vector flow: A new
external force for snakes. In CVPR97, pages 66–71.
INTERPOLATION SNAKES FOR BORDER DETECTION IN ULTRASOUND IMAGES
305
