
ANALYSIS OF AN EXTENDED PMART FOR CT IMAGE
RECONSTRUCTION AS A NONLINEAR DYNAMICAL SYSTEM
Tetsuya Yoshinaga
The University of Tokushima
3-18-15 Kuramoto, Tokushima, 770-8509 Japan
Keywords:
CT, iterative image reconstruction, PMART, nonlinear dynamical system, bifurcation.
Abstract:
Among iterative image reconstruction algorithms for computed tomography (CT), it is known that the power
multiplicative algebraic reconstruction technique (PMART) has a good property for convergence speed and
maximization of entropy. In this paper, we investigate an extended PMART, which is a dynamical class for ac-
celerating the convergence. The convergence process of the state in the neighborhood of the true reconstructed
image can be reduced to the property of a fixed point observed in the dynamical system. For investigating
convergence speed, we present a computational method of obtaining parameter sets in which a given real or
absolute value of the characteristic multiplier is equal. The advantage of the extended PMART is verified
by comparing with the standard multiplicative algebraic reconstruction technique (MART) using numerical
experiments.
1 INTRODUCTION
Iterative reconstruction technique (Gordon et al.,
1970; Kak and Slaney, 1987; Stark, 1987; Shepp
and Vardi, 1982) is known as a method to recon-
struct images of computed tomography (CT), and
has advantages for reducing artifacts against the fil-
tered backprojection procedure, which is commonly
used for CT reconstruction in practice. Because of
the high-quality reconstructions, there has been a
lot of research (Gordon and Herman, 1974; Snyder
et al., 1992; Herman and Meyer, 1993; Wang et al.,
1996; Mueller et al., 1999; Man et al., 2001; Byrne,
2004) improving the iterative deblurring procedures.
Among the iterative reconstruction algorithms, the
power multiplicative algebraic reconstruction tech-
nique (PMART) (Badea and Gordon, 2004; Byrne,
2004) has a good property for maximizing entropy,
however, it requires a large number of iterations to ob-
tain the final reconstruction image for large data sets.
In order to improve the convergence speed, we pro-
pose an extended PMART, which is a dynamical class
including the multiplicative algebraic reconstruction
technique (MART) as well as the PMART. The con-
vergence process of the state in the neighborhood of
the true reconstructed image can be reduced to the
property of a fixed point observed in the dynamical
system. For investigating convergence behavior, we
present a computational method of obtaining parame-
ter sets in which a given real or absolute value of the
characteristic multiplier is equal. The advantage of
the extended PMART is verified by comparing with
the standard MART using numerical experiments.
2 METHOD OF ANALYSIS
Each iterative reconstruction procedure treated in this
paper is considered as a nonlinear dynamical system.
Theoretical background and methods for analysis us-
ing qualitative bifurcation theory are summarized in
this section. The procedure of numerical calculation
in Sect.2.2 is a novel method for the purpose of study-
ing convergence process observed in the dynamical
system.
2.1 Fixed Point and its Bifurcation
We consider a discrete dynamical system or a general
map defined by
T
ν
: R
n
→ R
n
; x
(k)
→ x
(k+1)
= T
ν
(x
(k)
) (1)
where x ∈ R
n
is the state of discrete time k =
1, 2,..., and ν ∈ R is a system parameter. The point
440
Yoshinaga T. (2006).
ANALYSIS OF AN EXTENDED PMART FOR CT IMAGE RECONSTRUCTION AS A NONLINEAR DYNAMICAL SYSTEM.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 440-444
DOI: 10.5220/0001364304400444
Copyright
c
SciTePress

x
∗
satisfying
x
∗
− T
m
ν
(x
∗
)=0 (2)
becomes a fixed (m =1)oranm-periodic (m>1)
point of T
ν
. Let x
∗
be a periodic point of T
ν
, then
the characteristic equation of the periodic point x
∗
is
defined by
χ(x
∗
,ν,µ) = det(µE − DT
m
ν
(x
∗
)) = 0 (3)
where E is the n × n identity matrix, and DT
m
ν
de-
notes the derivative of T
m
ν
. We call x
∗
is hyperbolic,
if all the absolute values of the eigenvalues of T
m
ν
are
different from unity. Note that an m-periodic point
can be studied by replacing T
ν
with T
m
ν
, mth iterates
of T
ν
, in Eq.(2). Therefore in the following we con-
sider only properties of a fixed point of T
ν
. Similar
argument can be applied to the periodic point of T
ν
.
Now we consider a topological classification of hy-
perbolic fixed point. Let x
∗
be a hyperbolic fixed
point and E
u
be the intersection of R
n
and the di-
rect sum of the generalized eigenspaces of DT
ν
(x
∗
)
corresponding to the eigenvalues µ such that |µ| > 1.
Let L
u
= DT
ν
(x
∗
)|
E
u
. Then the topological type
of a hyperbolic fixed point is determined by dim E
u
and the orientation preserving or reserving property
of L
u
.
We define four types of hyperbolic fixed points:
1. PD-type if dim E
u
is even and det L
u
> 0,
2. ND-type if dim E
u
is odd and det L
u
> 0,
3. PI-type if dim E
u
is even and det L
u
< 0, and
4. NI-type if dim E
u
is odd and det L
u
< 0.
From the definition, at a PD-oranND-type of fixed
point x
∗
, L
u
is an orientation preserving mapping,
whereas at a PI-oranNI-type of fixed point x
∗
,
T
ν
is an orientation reversing mapping. If E
u
is the
empty set, we identify x
∗
as a PD-type. We use the
symbol
M
m
for a hyperbolic periodic point, where
M denotes one of the types PD, ND, PI and NI,
and indicates the number of characteristic multiplier
outside the unit circle in the complex plane, and m
indicates m-periodic point, which will be omitted for
m =1.
Bifurcation occurs when the topological type of
a fixed point is changed by the variation of a sys-
tem parameter. The generic codimension-one bifurca-
tions are: tangent bifurcation, period-doubling bifur-
cation, and the Neimark-Sacker bifurcation. These bi-
furcations are observed when the hyperbolicity is de-
stroyed, which corresponds to the critical distribution
of the characteristic multiplier µ such that µ =+1
for tangent bifurcation, µ = −1 for period-doubling
bifurcation, and µ = e
jθ
for the Neimark-Sacker bi-
furcation, where j =
√
−1.
2.2 Equal Characteristic Multiplier
The convergence behavior in the neighborhood of a
stable fixed point is governed by characteristic mul-
tipliers or eigenvalues of the derivative of T
ν
with
respect to the fixed point. To investigate parameter
region in which the system has locally faster conver-
gence speed, we propose a method for calculating a
set of both parameter and fixed point with a given
equal real or absolute value of the characteristic mul-
tiplier.
In the case of real characteristic multiplier:
When the specified real characteristic multiplier is de-
noted by µ
∗
, the condition is given by
χ(x, ν, µ
∗
) = det (µ
∗
E − DT
ν
(x)) = 0 (4)
Therefore we can obtain unknown set (x, ν) ∈ R
n
×
R by solving the fixed point equation of Eq.(2) and
the condition of Eq.(4), simultaneously.
In the case of complex characteristic multiplier:
When the specified absolute value of the characteris-
tic multiplier is denoted by ρ
∗
, the condition is given
by
χ(x, ν, ρ
∗
e
jθ
) = det
ρ
∗
e
jθ
E − DT
ν
(x)
=0 (5)
where j is the imaginary unit, and θ is the argument of
a complex characteristic multiplier. For obtaining un-
known set (x, ν, θ) ∈ R
n
×R ×R, we solve simulta-
neous equations consisting of the fixed point equation
Eq.(2) and the following two equations:
χ
1
(x, ν, ρ
∗
e
jθ
)=
det
ρ
∗
e
jθ
E − DT
ν
(x)
=0
χ
2
(x, ν, ρ
∗
e
jθ
)=
det
ρ
∗
e
jθ
E − DT
ν
(x)
=0
(6)
where and denote the real and the imaginary
parts, respectively.
For the numerical determination of the above sets,
Newton’s method is used. The Jacobian matrix of the
set of equations is derived from the first and the sec-
ond derivatives of the map T
ν
. This procedure is an
extension of Kawakami’s method (Kawakami, 1984)
for finding bifurcation parameters.
3 DYNAMICS OF AN EXTENDED
PMART
Consider a J-dimensional discrete dynamical system
x
(k+1)
= f (x
(k)
), k =1, 2,..., or a map defined by
f : R
J
→ R
J
; x → f(x) (7)
ANALYSIS OF AN EXTENDED PMART FOR CT IMAGE RECONSTRUCTION AS A NONLINEAR DYNAMICAL
SYSTEM
441

where x
(k)
and x =(x
1
,x
2
,...,x
J
)
T
are state vec-
tors in R
J
, each of which corresponds to the succes-
sive estimate of the reconstructed value of an iterative
algorithm in image reconstruction. The PMART can
be written in the mapping form with the following ele-
ments f
j
s for j =1, 2,...,J: f
j
= f
I
j
◦f
I−1
j
◦···◦f
1
j
with ith submap
f
i
j
= x
j
q
i
p
i
x
γp
i
j
(8)
where p
i
=
p
i
1
,p
i
2
,...,p
i
J
is the normalized projec-
tion operator applied on the x image, q
i
and p
i
x are
respectively the projection and the reprojection val-
ues, corresponding to the ith ray, for i =1, 2,...,I,
and γ is a positive real parameter.
The derivative of f with respect to x is given by
∂f
∂x
=
∂f
I
∂x
∂f
I−1
∂x
···
∂f
1
∂x
and the derivative of each
submap f
i
can be obtained by
∂f
i
∂x
= diag
j
q
i
p
i
x
γp
i
j
×
E −
γ
p
i
x
diag
j
{x
j
}·p
i
· p
i
T
for i =1, 2,...,I, where E denotes the J×J identity
matrix. By direct calculation, we see that the eigen-
values of the Jacobian ∂f
i
/∂x at a fixed point of f
are (1 − γ) and (J − 1) ones. Therefore when the
value of γ is 2 or the critical power (Badea and Gor-
don, 2004), the absolute values of the determinants of
the derivatives for the map f as well as each submap
f
i
at the fixed point are all 1, and every characteristic
multiplier of the fixed point is located on the unit cir-
cle in the complex plane. Moreover the fixed point is
stable and unstable when the values of γ are less and
greater than 2, respectively.
We now consider a dynamical system defined by
g : R
J
→ R
J
; x → (1 − λ)x + λf(x) (9)
where f denotes the map of the PMART in Eq.(7)
with Eq.(8), and λ ∈ R is a parameter. Note that
the expression Eq.(9) includes the algorithm of the
MART (Badea and Gordon, 2004) when λ =1and
γ =1.
As discussed above, in the case of J ≥ 2, a higher
codimension bifurcation satisfying multiple generic
bifurcation conditions including the Neimark-Sacker
bifurcation, of the nonhyperbolic fixed point occurs
in the dynamical system f at γ =2. Then an in-
variant closed curve (ICC) generates around the fixed
point in the state space. When γ<2, the ICC disap-
pears and iterative points converge to the stable fixed
point along the center manifold that is qualitatively
equivalent to the spiral. Due to the attracting spiral
behavior, it is expected that g(x), which is considered
Figure 1: Phantom image of 5 × 5 pixels.
as a weighted average of the point x and the next it-
erate f (x), obtains a better estimate than f(x) for an
appropriate value of λ.
4 EXPERIMENTAL RESULTS
AND DISCUSSION
To illustrate the efficiency of the proposed iterative al-
gorithm and the computational method, we treat two
examples: (i) the first image is made of four pixels
and six projection rays with the projection operator
p
1
=(1, 1, 0, 0), p
2
=(0, 0, 1, 1), p
3
=(1, 0, 0, 1),
p
4
=(0, 1, 0, 1), p
5
=(1, 0, 1, 0), and p
6
=
(0, 1, 1, 0), and the phantom image x
∗
=(5, 6, 7, 2)
T
;
and (ii) the image as the second example is made of
5 × 5 pixels and 56 projection rays with phantom im-
age shown in Fig.1.
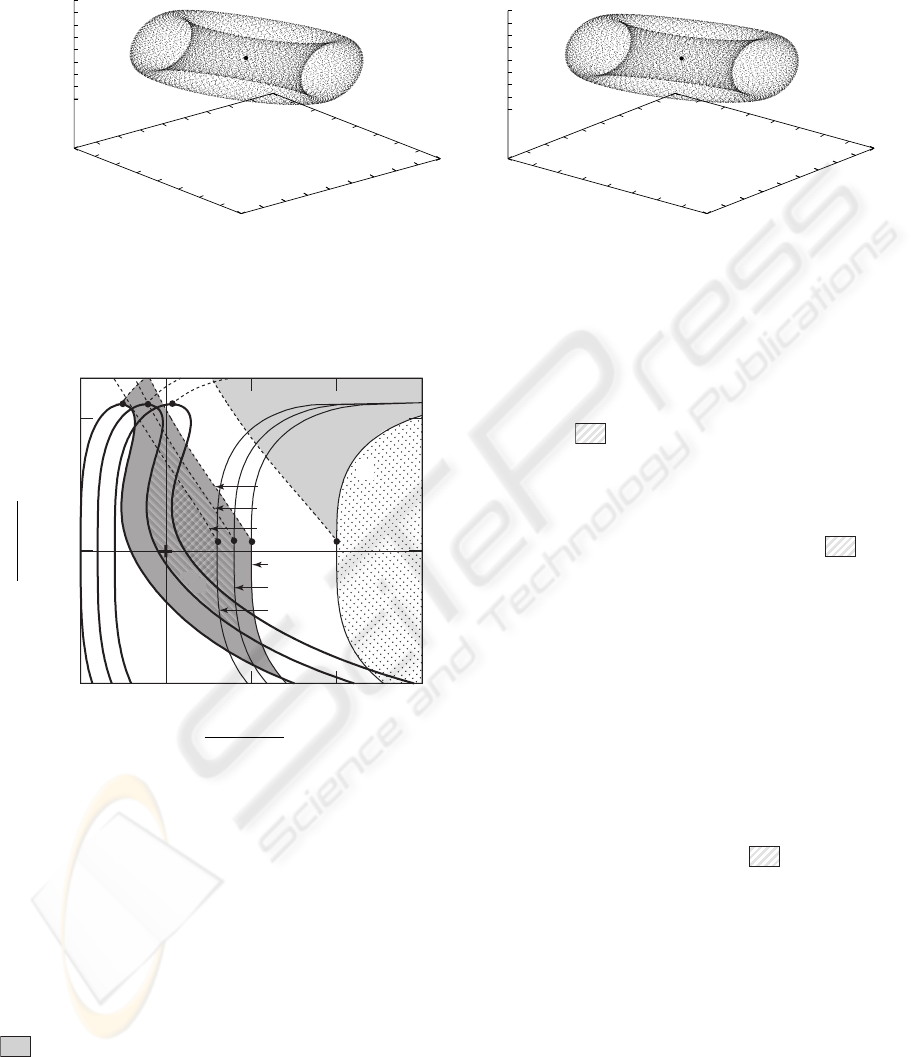
Figure 2 shows an ICC forming a torus observed in
the map f for the first example (J =4) with γ =2,
consisting of 100,000 iterated points. The characteris-
tic multipliers of the fixed point satisfy the condition
of the double Neimark-Sacker bifurcation as a codi-
mension two bifurcation.
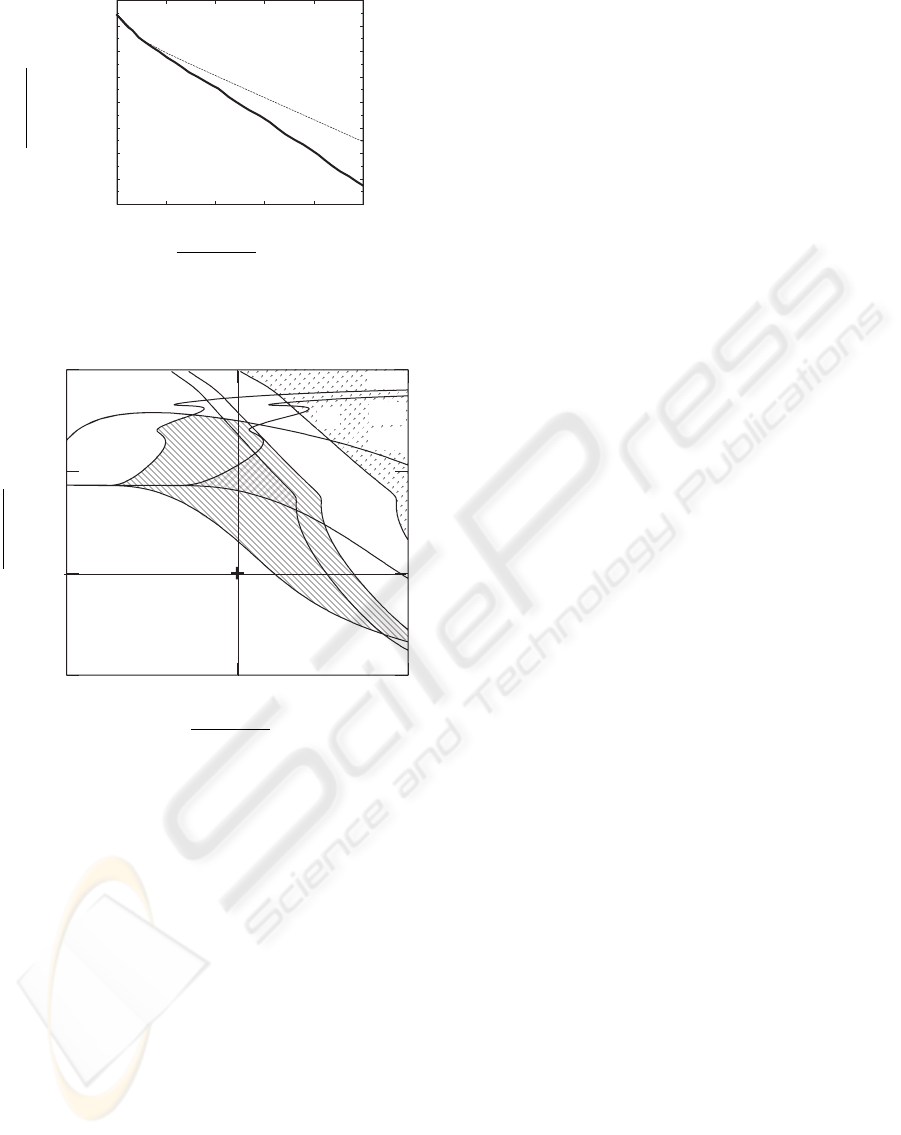
Figure 3 shows a phase transition diagram of fixed
points observed in the extended PMART of Eq.(9)
with J =4. In the figure, the parameter sets of equal
values of characteristic multipliers of fixed points are
indicated by solid and dashed curves with symbols
µ
∗
R and
ρ
∗
C, in the case of real multiplier µ
∗
and
the absolute value ρ
∗
of complex multiplier, respec-
tively, each of which is the maximum absolute value
among all characteristic multipliers. Period-doubling
and the Neimark-Sacker bifurcations are convention-
ally denoted by the symbols P and NS, which are
equivalent to
−1
R and
1
C, respectively.
In the diagram, there exists a unique stable fixed
point in the parameter regions without shading, and
with shading patterns
, and . Whereas,
in the regions with patterns
and surrounded
by the Neimark-Sacker and period-doubling bifurca-
tion curves, the fixed point is unstable and a solution
does not converge to the fixed point corresponding to
the phantom image. By increasing the value of λ for
fixed, e.g., γ =0.9, through the bifurcation curve P ,
VISAPP 2006 - IMAGE ANALYSIS
442
4.8
4.85
4.9
4.95
5
5.05
5.1
5.15
5.2
x1
5.8
5.85
5.9
5.95
6
6.05
6.1
6.15
6.2
6.25
x2
6.8
6.85
6.9
6.95
7
7.05
7.1
7.15
7.2
x3
4.8
4.85
4.9
4.95
5
5.05
5.1
5.15
5.2
x1
5.8
5.85
5.9
5.95
6
6.05
6.1
6.15
6.2
6.25
x2
6.8
6.85
6.9
6.95
7
7.05
7.1
7.15
7.2
x3
Figure 2: Perspective figure of an ICC observed in f with γ =2. The fixed point is located at the circled point in the center
of iterated points.
γ
-
0.5
1
1.5
0.5 1 1.5 2 2.5
R
-0.3
R
-0.4
R
-0.5
NS
R
0.4
C
0.3
C
0.4
C
0.5
R
0.5
P
R
0.3
λ
-
Figure 3: Phase transition of fixed points observed in g with
J =4.
the bifurcation formula is given by
0
PD →
1
PI +
0
PD
2
where the left- and right-hand sides of the arrow in-
dicate invariant sets before and after the bifurcation,
respectively. On the other hand, when the parameters
pass through the Neimark-Sacker bifurcation curve
NS in the direction from outside to inside the region
, we have the following formula:
0
PD →
2
PD+ ICC
The parameter curves of equal characteristic mul-
tipliers are shown in the case of 0.3, 0.4 and 0.5 as
their maximum absolute values. We see that there is a
fixed point with characteristic multipliers whose max-
imum absolute value is less than 0.3, in the region
with pattern
. Therefore, a parameter in this re-
gion gives a faster convergence in the neighborhood
of the stable fixed point. Note that the system at the
parameter (λ, γ)=(1, 1), denoted by the symbol
+
in the diagram, corresponds to the MART, and the pa-
rameter point is located outside the region
. In-
deed, a simulation result compared with the extended
PMART at (λ, γ)=(1.2, 1.05) and the MART is il-
lustrated in Fig.4, showing the root mean square dis-
tance between the reconstructed value and the fixed
point, normalized by the standard deviation (Gordon
and Herman, 1974), for the time series. The initial
state for the iterations was set to a constant image. In
the figure, the lines (a) and (b) are results using the
extended PMART and the MART, respectively. We
see that the proposed method gives rise to faster con-
vergence with a steep slope in log scale.
A phase transition for the second example (J =25)
is shown in Fig.5. Similarly as the first example,
we see that the parameter region
, in which the
maximum absolute of characteristic multiplier is min-
imum, does not include the parameter point (λ, γ)=
(1, 1).
5 CONCLUSION
We have investigated an extended PMART proposed
in order to accelerate the convergence. For analyz-
ing convergence speed in the neighborhood of the sta-
ble fixed point, we have proposed a computational
method to calculate a set of equal value of characteris-
tic multipliers, based on the dynamical system theory.
ANALYSIS OF AN EXTENDED PMART FOR CT IMAGE RECONSTRUCTION AS A NONLINEAR DYNAMICAL
SYSTEM
443
d
-
1e-14
1e-12
1e-10
1e-08
1e-06
0.0001
0.01
1
100
0 2 4 6 8 10
(b)
(a)
k
-
Figure 4: The distance d for the time series of (a) the ex-
tended PMART and (b) the MART.
γ
-
0.5
1
1.5
2
0.5 1 1.5
R
0.7
-0.7
R
R
-0.6
R
0.6
C
0.7
C
0.6
P
C
0.7
λ
-
Figure 5: Phase transition of fixed points observed in g with
J =25.
Then, by numerical experiments of lower dimensional
systems, we have obtained a parameter region which
gives a faster convergence than the original MART.
The performance of the acceleration depends on the
dynamical property of the system with the parameters
γ and λ. We should investigate the theoretical reason
why the parameter region in which the maximum ab-
solute value of characteristic multiplier is minimum,
excludes the value (λ, γ)=(1, 1).
REFERENCES
Badea, C. and Gordon, R. (2004). Experiments with the
nonlinear and chaotic behaviour of the multiplicative
algebraic reconstruction technique (MART) algorithm
for computed tomography. Phys. Med. Biol., 49:1455–
1474.
Byrne, C. (2004). A unified treatment of some iterative al-
gorithms in signal processing and image reconstruc-
tion. Inverse Problems, 20:103–120.
Gordon, R., Bender, R., and Herman, G. (1970). Algebraic
reconstruction technique (ART) for three-dimensional
electron microscopy and x-ray photography. J. Theo-
ret. Biol., 29:471–482.
Gordon, R. and Herman, G. (1974). Three dimensional re-
construction from projections: a review of algorithms.
Int. Rev. Cytol., 38:111–151.
Herman, G. and Meyer, L. (1993). Algebraic reconstruc-
tion techniques can be made computationally efficient.
IEEE Trans. Med. Imag., 12(3):600–609.
Kak, A. and Slaney, M. (1987). Principles of Computerized
Tomographic Imaging. Piscataway, NJ: IEEE Press.
Kawakami, H. (1984). Bifurcation of periodic responses
in forced dynamic nonlinear circuits: computation of
bifurcation values of the system parameters. IEEE
Trans. Circuits and Systems, CAS-31(3):246–260.
Man, B., Nuyts, J., Dupont, P., Marchal, G., and Suetens, P.
(2001). An iterative maximum-likelihood polychro-
matic algorithm for CT. IEEE Trans. Med. Imag.,
20(10):999–1008.
Mueller, K., Yagel, R., and Wheller, J. (1999). Anti-aliases
three-dimensional cone-beam reconstruction of low-
contrast objects with algebraic methods. IEEE Trans.
Med. Imag., 18(6):519–537.
Shepp, L. and Vardi, Y. (1982). Maximum likelihood re-
construction in positron emission tomography. IEEE
Trans. Med. Imag., 1:113–122.
Snyder, D., Schulz, T., and O’Sullivan, J. (1992). Deblur-
ring subject to nonnegativity constraints. IEEE Trans.
Signal Processing, 40(5):1143–1150.
Stark, H. (1987). Image Recovery: Theory and Application.
FL: Academic.
Wang, G., Snyder, D., O’Sullivan, J., and Vannier, M.
(1996). Iterative deblurring for CT metal artifact re-
duction. IEEE Trans. Med. Imag., 15(5):657–664.
VISAPP 2006 - IMAGE ANALYSIS
444
